Cheban D.N. Global Attractors Of Non-autonomous Dissipative Dynamical Systems

Подождите немного. Документ загружается.

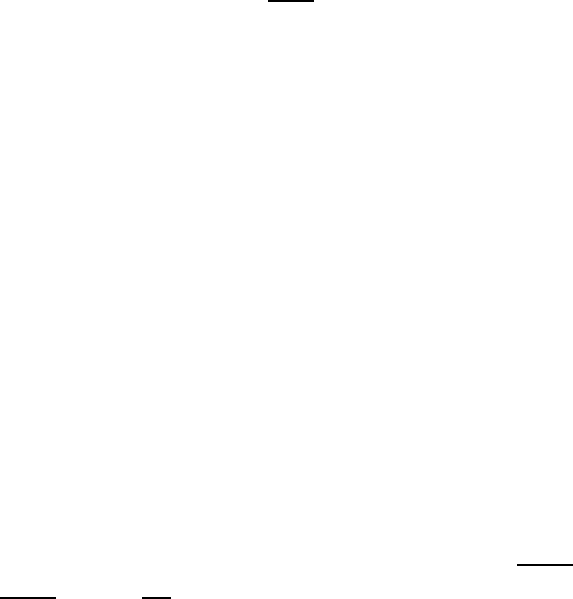
September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

Triangular maps 467

kνk ≤ N

1 + q

1 − q

kfk.

Proof. This aﬃrmations follows directly from Theorem 14.1 and Lemmas 14.1 and

14.2. 

Deﬁnition 14.7 A dynamical system (Ω, Z

, σ) is said to be invertible, if the

map f := σ(1, ·) : Ω → Ω is invertible and, consequently, on Ω there is deﬁned a

group dynamical system (Ω, Z, σ), where π(−n, ·) := (π(n, ·)

−1

Remark 14.1 In case the dynamical system (Ω, Z

, σ) is invertible, Theorem

14.2 is well known (see, for example,

[

122

]

14.3 Quasi-linear non-autonomous dynamical systems

Let us consider the following quasi-linear equation

n+1

= A(σ

ω)u

+ f(σ

ω) + F (σ

ω, u

), (14.15)

where A ∈ C(Ω, L(E)), f ∈ C(Ω, E) and F ∈ C(Ω × E, E).

Theorem 14.3 Assume that there exist positive numbers L < L

1−q

N(1+q)

and

r < r

:= ε

N(1+q)

1−q

(1 − N L

1+q

1−q

)

−1

such that

kF (ω, x

) − F (ω, x

)k ≤ Lkx

−x

for all ω ∈ Ω and x

, x

∈ B[Q, r] = {x ∈ E | ρ(x, Q) ≤ r}, where Q := ν(Ω),

ν ∈ C(Ω, E) is the unique function from C(Ω, E) ﬁguring in Theorem 14.2 and

= max

ω∈Ω

kF (ω, ν(ω))k. Then there exists a function w ∈ C(Ω, B[Q, r]) such that

w(σ

ω) = ψ(n, w(ω), ω)

for all n ∈ Z

and ω ∈ Ω, where ψ(·, u, ω) is the unique solution of quasi-linear

equation (14.15) with the initial condition ψ(0, u, ω) = u.

Proof. Let u := v + ν(σ

ω). Then from equation (14.15) we get

n+1

= A(σ

ω)v

+ F (σ

ω, v + ν(σ

ω)).

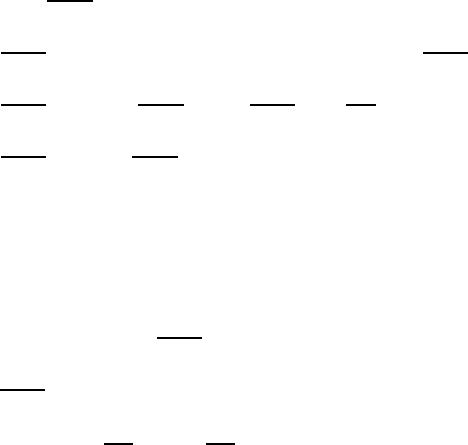
September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

468 Global Attractors of Non-autonomous Dissipative Dynamical Systems

Let 0 < r < r

and α ∈ C(Ω, B[Q, r]), where B[Q, r] := {u ∈ E | ρ(u, Q) ≤ r}.

Consider the equation

n+1

= A(σ

ω)v

f(σ

ω),

where

f(ω) := F (ω, α(ω) + ν(ω)) for all ω ∈ Ω. According to Theorem 14.2, there

exists a unique function ν

∈ C(Ω, E) with properties a. and b. In virtue of

Theorem 14.2, we have

kν

k ≤ N

1 + q

1 − q

max

ω∈Ω

kF (ω, α(ω) + ν(ω))k

≤ N

1 + q

1 − q

max

ω∈Ω

|F (ω, α(ω) + ν(ω)) −F (ω, γ(ω))|+ N

1 + q

1 − q

max

ω∈Ω

|F (ω, γ(ω))|

≤ N

1 + q

1 − q

Lkαk+ N

1 + q

1 − q

≤ N

1 + q

1 − q

Lr +

≤ N

1 + q

1 − q

+ N

1 + q

1 − q

= r

and, consequently, F(C(Ω, B[Q, r

])) ⊆ C(Ω, B[Q, r

]), where F : C(Ω, B[Q, r])) →

C(Ω, E) is the map deﬁned by the equality F(α) := ν

Now we will show that the map F : C(Ω, B[Q, r

]) → C(Ω, B[Q, r

]) is a Lips-

chitzian one. In fact, according to Theorem 14.2 we have

kF(α

) − F(α

)k ≤ N

1 + q

1 − q

max

ω∈Ω

|F (ω, α

(ω) + ν(ω)) − F (ω, α

(ω) + ν(ω))|

≤ N

1 + q

1 − q

L max

ω∈Ω

|α

(ω) − α

(ω)|.

We note that N

1+q

1−q

L ≤ N

1+q

1−q

< 1. Thus, the map F is a contraction

and, consequently, by Banach ﬁxed point theorem, there exists a unique function

α ∈ C(Ω, B[Q, r

]) such that F(α) = α. To ﬁnish the proof of the theorem it is

suﬃcient to put w := γ + α. 

We now consider a perturbed quasi-linear equation

n+1

= A(σ

ω)u

+ f(σ

ω) + λF (σ

ω, u

), (14.16)

where λ ∈ [−λ

, λ

] (λ

> 0) is a small parameter.

Theorem 14.4 Assume that there exist positive numbers r and L such that

|F (ω, u

) − F (ω, u

)| ≤ L|u

−u

for all ω ∈ Ω and u

, u

∈ B[Q, r]. Then for λ small enough there exists a unique

function ν

∈ C(Ω, B[Q, r]) such that

(σ

ω) = ψ

(n, ν

(ω), ω)

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

Triangular maps 469

for all n ∈ Z

and ω ∈ Ω, where ψ

(·, u, ω) is the unique solution of equation

(14.16) with the initial condition ψ

(0, u, ω) = u. Moreover,

lim

λ→0

max

ω∈Ω

|ν

(ω) − ν(ω)| = 0, (14.17)

where ν ∈ C(ω, E) is deﬁned in Theorem 14.2.

Proof. We can prove the existence of ν

by a slight modiﬁcation of the proof of

Theorem 14.3.

To prove (14.17) we note that

|F (ω, ν

(ω))| ≤ |F (ω, ν

(ω)) − F (ω, ν(ω))|+ |F (ω, ν(ω))| ≤ Lr + ε

Denote ∆

(ω) := ν

(ω) − ν(ω) (ω ∈ Ω). It is easy to see that the sequence

{∆

(σ

ω)}

n∈Z

is the unique bounded on Z solution of the equation

n+1

= A(σ

ω)z

+ λF (σ

ω, ν

(σ

(ω))

and, consequently,

|ν

(σ

ω) −ν(σ

ω)| = |∆(σ

ω)|N

1 + q

1 − q

(14.18)

×sup

n∈Z

|λF (σ

ω, ν

(σ

ω)| ≤ |λ|N

1 + q

1 − q

(Lr + ε

)

for all ω ∈ Ω, n ∈ Z and λ ∈ [−λ

, λ

]. Thus, from inequality (14.18) we obtain

|ν

(ω) − ν(ω)| ≤ |λ|N

1 + q

1 − q

(Lr + ε

) (14.19)

for all ω ∈ Ω and λ ∈ [−λ

, λ

]. Passing to limit in inequality (14.19) as λ → 0, we

obtain (14.17). 

14.4 Global attractors of quasi-linear triangular systems

Consider a diﬀerence equation

n+1

= f(σ

ω, u

) (ω ∈ Ω). (14.20)

Denote by ϕ(n, u, ω) a unique solution of equation (14.20) with the initial condition

ϕ(0, u, ω) = u.

Deﬁnition 14.8 Equation (14.20) is said to be dissipative, if there exists a posi-

tive number r such that

lim sup

n→+∞

|ϕ(n, u, ω)| ≤ r

for all u ∈ E and ω ∈ Ω.

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

470 Global Attractors of Non-autonomous Dissipative Dynamical Systems

Consider a quasi-linear equation

n+1

= A(σ

ω)u

+ F (σ

ω, u

), (14.21)

where A ∈ C(Ω, [E]) and the function F ∈ C(Ω × E, E) satisﬁes to ”the condition

of smallness”.

Denote by U(k, ω) the Cauchy’s matrix for the linear equation

n+1

= A(σ

ω)u

Theorem 14.5 Suppose that the following conditions hold:

(1) there are positive numbers N and q < 1 such that

kU(n, ω)k ≤ Mq

(n ∈ Z

); (14.22)

(2) |F (ω, u)| ≤ C + D|u| (C ≥ 0, 0 ≤ D < (1 − q)N

−1

) for all u ∈ E and ω ∈ Ω.

Then equation (14.21) is dissipative.

Proof. Let ϕ(·, u, ω) be the solution of equation (14.21) passing through the point

u ∈ E for n = 0. According to the formula of the variation of constants (see, for

example,

[

170

]

and

[

188

]

) we have

ϕ(n, u, ω) = U(k, ω)u +

n−1

m=0

U(n − m −1, ω)F (σ

ω, ϕ(m, u, ω)),

and, consequently,

|ϕ(n, u, ω)| ≤ N q

|u|+

n−1

m=0

n−m−1

(C + D|ϕ(m, u, ω)|). (14.23)

We set u(n) := q

−n

|ϕ(n, u, ω)| and, taking into account (14.23), obtain

u(n) ≤ N|u| + CN q

−1

n−1

m=0

−m

+ DNq

−1

n−1

m=0

u(m). (14.24)

Denote the right hand side of inequality (14.24) by v(n). Note, that

v(n + 1) −v(n) = q

−n

u(n) ≤

v(n) +

−n

and,hence,

v(n + 1) ≤



1 +



v(n) +

−n

From this inequality we obtain

v(n) ≤



1 +



n−1

v(1) +

1 − q

n−1

1 −q

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

Triangular maps 471

Therefore,

|ϕ(n, u, ω)| ≤ (q + DN )

n−1

qN|u| +

q − 1

n−1

−1), (14.25)

because v(1) = N |u|. From (14.25) follows that

lim sup

k→+∞

|ϕ(n, u, ω)| ≤

1 − q

for all u ∈ E and ω ∈ Ω. The theorem is proved. 

Let hE, ϕ, (Ω, Z

, σ)i be a cocycle over (Ω, Z

, σ) with the ﬁber E.

Deﬁnition 14.9 Recall that a family {I

| ω ∈ Ω}(I

⊂ E) of nonempty com-

pact subsets is called a compact global attractor of the cocycle ϕ, if the following

conditions are fulﬁlled:

(1) the set

| ω ∈ Ω} is relatively compact;

(2) the family I := {I

| ω ∈ Ω} is invariant with respect to the cocycle ϕ, i.e.

ϕ(n, I

, ω) = I

for all n ∈ Z

and ω ∈ Ω;

(3) the equality

lim

n→+∞

sup

ω∈Ω

β(ϕ(n, K, ω), I) = 0

takes place for every K ∈ C(E), where C(E) is a family of all compacts from

Deﬁnition 14.10 A cocycle hE, ϕ, (Ω, T, σ)i is said to be dissipative, if there

exists a positive number r such that

lim sup

n→+∞

|ϕ(n, u, ω)| ≤ r

for all u ∈ E and ω ∈ Ω.

Theorem 14.6 (

[

102

]

) Every dissipative cocycle hE, ϕ, (Ω, T, σ)i admits a com-

pact global attractor {I

| ω ∈ Ω} such that:

(1) the component I

(ω ∈ Ω) is connected;

(2) the set I =

| ω ∈ Ω} is connected, if the space Ω also is.

Theorem 14.7 Under the conditions of Theorem 14.5, equation (14.21) (i.e. the

cocycle ϕ generated by equation (14.21)) admits a compact global attractor {I

| ω ∈

Ω} with the following properties:

(1) the component I

(ω ∈ Ω) is connected;

(2) the set I =

| ω ∈ Ω} is connected, if the space Ω also is.

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

472 Global Attractors of Non-autonomous Dissipative Dynamical Systems

Proof. This statement follows directly from Theorems 14.5 and 14.6. 

Deﬁnition 14.11 Recall that a cocycle hE, ϕ, (Ω, T, σ)i is said to be convergent,

if it admits a compact global attractor {I

| ω ∈ Ω} such that every component I

(ω ∈ Ω) contains a single point u

, i.e. I

= {u

} (ω ∈ Ω).

Theorem 14.8

[

102, Ch.2

]

Let hE, ϕ, (Ω, T, σ)i be a cocycle admitting a compact

global attractor I = {I

| ω ∈ Ω}. If

lim

n→+∞

max

|,|u

|≤r,ω∈Ω

|ϕ(n, u

, ω) −ϕ(n, u

, ω)| = 0 (14.26)

for every r > 0, then the set I

contains a single point for every ω ∈ Ω.

Theorem 14.9 Let A ∈ C(Ω, [E]) and F ∈ C(Ω × E, E) and the following con-

ditions be fulﬁlled:

(1) there exist positive numbers N and q < 1 such that inequality (14.22) holds;

(2) |F (ω, u

) − F (ω, u

)| ≤ L|u

− u

| (0 ≤ L < N

−1

(1 − q)) for all ω ∈ Ω and

, u

∈ E.

Then equation (14.21) is convergent, i.e. the cocycle generated by this equation

is convergent.

Proof. First step. We will prove that under the conditions of Theorem 14.9 equation

(14.21) admits a compact global attractor I = {I

| ω ∈ Ω}. In fact,

|F (ω, u)| ≤ |F (ω, 0)| + L|u| ≤ C + L|u|

for all u ∈ E, where C := max{|F (ω, 0)| | ω ∈ Ω}. According to Theorems 14.5 and

14.6, the equation (14.21) admits a compact global attractor I = {I

| ω ∈ Ω}.

Second step. Let ϕ be the cocycle generated by equation (14.21). In virtue of

the formula of the variation of constants, we have

ϕ(n, u, ω) = U(n, ω)u +

n−1

m=0

U(n − m −1, ω)F (σ

ω, ϕ(m, u, ω)).

Consequently,

ϕ(n, u

, ω) −ϕ(n, u

, ω) = U (n, ω)(u

−u

n−1

m=1

U(n −m −1, A)[F (σ

ω, ϕ(m, u, ω)) − F (σ

ω, ϕ(m, u

, ω)].

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

Triangular maps 473

Thus,

|ϕ(n, u

, ω) −ϕ(n, u

, ω)| ≤ Nq

(|u

−u

+Lq

−1

n−1

m=0

−m

|ϕ(m, u

, ω) −ϕ(m, u

, ω)|). (14.27)

Let u(n) := |ϕ(n, u

, ω) −ϕ(n, u

, ω)|q

−n

. From (14.27) follows that

u(n) ≤ N



−u

|+ Lq

−1

n−1

m=0

u(m)



. (14.28)

Denote by v(n) the right hand side of (14.28). The following inequality

v(n + 1) −v(n) = LNq

−1

u(n) ≤ LNq

−1

v(n). (14.29)

holds. From (14.29) we obtain

v(n) ≤ (1 + LN q

−1

)

n−1

v(1)

and, since v(1) = N|u

−u

|, we get

u(n) ≤ (1 + LNq

−1

)N|u

−u

|. (14.30)

From (14.30) we have

|ϕ(n, u

, ω) − ϕ(n, u

, ω)| ≤ (q + LM)

n−1

qN|u

−u

for all u

, u

∈ E and ω ∈ Ω.

To ﬁnish the proof of Theorem 14.9 it is suﬃcient to refer to Theorem 14.8. The

theorem is proved. 

Remark 14.2 Simple examples show that under the conditions of Theorem 14.7

the compact global attractor {I

| ω ∈ Ω}, generally speaking, is not trivial, i.e. the

component set I

contains more than one point. This statement can be illustrated

by the following example: u

1+u

Theorem 14.10 Let A ∈ C(Ω, [E]), F ∈ C(Ω×E, E) and the following conditions

be fulﬁlled:

(1) there are positive numbers N and q < 1 such that

kU(n, ω)k ≤ Nq

(n ≥ 0, ω ∈ Ω);

(2) |F (ω, u)| ≤ M + ε|u| ( u ∈ E, ω ∈ Ω ) and 0 ≤ ε ≤ ε

1−q

N(1+q)

;

(3) the restriction F

of the function F on Ω × B[0, r

], where r

:= NM

1+q

1−q

(1 −

1+q

1−q

)

−1

, satisﬁes the condition of Lipschitz with the Lipschitz’s constant

Lip(F

) <

1−q

N(1+q)

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

474 Global Attractors of Non-autonomous Dissipative Dynamical Systems

Then the following statements hold:

a. equation (14.21) admits a compact global attractor I = {I

| ω ∈ Ω};

b. there exists a continuous function ν : Ω → E satisfying the following conditions:

b1. the equality

ν(σ(n, ω)) = ϕ(n, ν(ω), ω)

holds for all n ∈ Z

and ω ∈ Ω, where ϕ(n, u, ω) is the unique solution of

equation (14.21) with the initial condition ϕ(0, u, ω) = u.

b2.

ν(ω) ∈ I

for all ω ∈ Ω.

Proof. The ﬁrst statement follows directly from Theorems 14.5 and 14.7.

We will prove now the second aﬃrmation. Deﬁne an operator F :

C(Ω, B[0, r

]) → C(Ω, E) in the following way. Let α ∈ C(Ω, B[0, r

]), then under

the conditions of Theorem 14.10 we have

f(·) := F (·, α(·)) ∈ C(Ω, B[0, r

]). Accord-

ing to Theorem 14.2, there exists a unique function ν

∈ C(Ω, E) with properties

a. and b. In virtue of Theorem 14.2, we have

kν

k ≤ N

1 + q

1 − q

max

ω∈Ω

|F (ω, α(ω))|

≤ N

1 + q

1 − q

(M + ε

kαk) ≤ N

1 + q

1 − q

(M + ε

) ≤ r

and, consequently, F(C(Ω, B[Q, r

])) ⊆ C(Ω, B[Q, r

]), where F : C(Ω, B[Q, r])) →

C(Ω, E) is the map deﬁned by the equality F(α) := ν

Now we will show that the map F : C(Ω, B[Q, r

]) → C(Ω, B[Q, r

]) is Lips-

chitzian. In fact, according to Theorem 14.2 we have

kF(α

) − F(α

)k ≤ N

1 + q

1 − q

max

ω∈Ω

|F (ω, α

(ω)) − F (ω, α

(ω)|

≤ N

1 + q

1 − q

L max

ω∈Ω

|α

(ω) − α

(ω)|.

We note that N

1+q

1−q

L ≤ N

1+q

1−q

< 1. Thus, the map F is a contraction and,

consequently, in virtue of the Banach’s ﬁxed point theorem there exists a unique

function w ∈ C(Ω, B[Q, r

]) such that F(w) = w. It is easy to see that w satisﬁes

the ﬁrst condition. To ﬁnish the proof of the theorem it is suﬃcient to remark that

the set A :=

| ω ∈ Ω}, where A

:= {w(ω)} × {ω}, is a compact invariant

set in the skew-product dynamical system (X, Z

, π) (X := E ×Ω and π := (ϕ, σ))

and J :=

| ω ∈ Ω} is a maximal compact invariant set of this system. Thus,

we have A ⊂ J and, consequently, w(ω) ∈ I

for all ω ∈ Ω. 

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

Triangular maps 475

Remark 14.3 Under the conditions of Theorem 14.10, dissipativity does not re-

duce to convergence.

We will give an example which conﬁrms this statement.

Example 14.1 Let k ∈ (

, 1). Consider a scalar equation

n+1

= ku

+ αF (u

) , (14.31)

where

F (x) :=

(

for |x| ≤ 10

50 + 10[1 − exp(10 −|x|)] for |x| > 10

for k < 1 < k + 5α. We can take r

2(1−k)

, then it is easy to check that for

equation (14.31) all the conditions of Theorem 14.10 are fulﬁlled for chosen α, k,

and F . In addition, its Levinson’s center (compact global attractor) contains at

least two ﬁxed points (in fact, there are 3 of them) and, consequently, equation

(14.31) is not convergent.

14.5 Almost periodic and recurrent solutions

Let (X, Z

, π) be a dynamical system, x ∈ X, m ∈ Z

, m > 0, ε > 0.

Denote M

= {{t

} | {xt

} is convergent}.

Theorem 14.11 (

[

300

]

[

302

]

) Let (X, Z

, π) and (Y, Z

, σ) be two dynamical

systems. Assume that h : X → Y is a homomorphism of (X, Z

, π) onto (Y, Z

, σ).

If a point x ∈ X is stationary (m-periodic, almost periodic, recurrent), then the point

y := h(x) is also stationary (m-periodic, almost periodic, recurrent) and M

⊂ M

Deﬁnition 14.12 A solution ϕ(n, u, ω) of equation (14.20) is said to be sta-

tionary (m-periodic, almost periodic, recurrent), if the point x := (u, ω) ∈ X :=

E × Ω is a stationary (m-periodic, almost periodic, recurrent) point of the skew-

product dynamical system (X, Z

, π), where π := (ϕ, σ), i.e. π(n, (u, ω)) :=

(ϕ(n, u, ω), σ(n, ω)) for all n ∈ Z

and (u, ω) ∈ E × Ω.

Lemma 14.3 Suppose that u ∈ C(Ω, E) satisﬁes the condition

u(σ(n, ω)) = ϕ(n, u(ω), ω) (14.32)

for all n ∈ Z

and ω ∈ Ω. Then the map h : Ω → X, deﬁned by

h(ω) := (u(ω), ω) (14.33)

for all ω ∈ Ω, is a homomorphism of (Ω, Z

, σ) onto (X, Z

, π).

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 14

476 Global Attractors of Non-autonomous Dissipative Dynamical Systems

Proof. This assertion follows from equalities (14.32) and (14.33) 

Remark 14.4 A function u ∈ C(Ω, E) with property (14.32) is called a con-

tinuous invariant section (or an integral manifold) of non-autonomous diﬀerence

equation (14.20).

Theorem 14.12 If a function u ∈ C(Ω, E) satisﬁes condition (14.32) and a

point ω ∈ Ω is stationary (m-periodic, almost periodic, recurrent), then the solution

ϕ(n, u(ω), ω) of equation (14.20) also is stationary (m-periodic, almost periodic,

recurrent).

Proof. This statement follows from Theorem 14.11 and Lemma 14.3. 

Using Theorem 14.12 and the results from sections 3 and 4we obtain some crite-

rions of the existence of periodic (almost periodic, recurrent) solutions of equation

(14.15). For example, the following statements hold.

Theorem 14.13 Let (Ω, Z

, π) be a dynamical system and Ω consists of m-

periodic (almost periodic, recurrent) points. Then under the conditions of Theorem

14.3 the equation (14.15) admits an invariant integral manifold consisting from m-

periodic (almost periodic, recurrent) solutions.

Theorem 14.14 Let (Ω, Z

, π) be a dynamical system and Ω consists of m-

periodic (almost periodic, recurrent) points. Under the conditions of Theorem 14.4

for a suﬃciently small λ the equation (14.16) admits a unique invariant mani-

fold ν

consisting from m-periodic (almost periodic, recurrent) solutions of equation

(14.16).

Example 14.2 Consider the equation

n+1

= f(n, u

) (14.34)

where f ∈ C(Z

×E, E); here C(Z

×E, E) is the space of all continuous functions

× E → E) equipped with a compact-open topology. This topology can be

metrized. For example, by the equality

d(f

, f

) :=

+∞

, d

)

1 + d

, d

)

where d

, d

) := max{ρ(f

(k, u), f

(k, u)) | k ∈ [0, n], |u| ≤ n}, there is deﬁned

a distance on C(Z

×E, E) which generates the topology of pointwise convergence

with respect to n ∈ Z

uniformly with respect to u on every compact from E.

Along with equation (14.34), we will consider the H-class of equation (14.34)

n+1

= g(n, v

) (g ∈ H(f )), (14.35)