Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.


3
21212
2dDYY >=−
. (11)
Для вычисления полуразмаха d
2
комбинируем выражения (9) и (11):
()
2
0,5
2/2;2
2
Yf
dStN
α
−
= . (12)
Найдём
доверительную вероятность
1 - Р, которой соответствуют доверительные
интервалы (10). Заменим величину f в уравнении (5) на 2f; α - на Р, S
Y
- на
2
Y
S
. Приравнивая
правые части равенств (5) и (12), получим зависимость Р от α и f в неявном виде:
t
P/2,
2f
= t
α/2,2f
•2
-0,5
. (13)
Здесь при больших значениях f (практически уже при f > 3) величина Р, в основном,
зависит от α. Эта зависимость в пределах 0,01
≤
α
≤
0,1, чаще всего используемых в
исследованиях [3], аппроксимирована уравнением [1, с. 26]:
1 - Р = 2 (1 -
α
) – 1,07 = 0,93 - 2
α
, (14)
где 1 – Р – искомая доверительная вероятность.
Пример 2. К условиям примера 1 добавим результат измерения величины Y
2
[5]:
{
}
4
1
2
=i
i
Y = {167; 171; 183; 194} при угле установки лопаток завихрителя 25°. Решить задачу 2, то
есть, определить, меняется ли перепад давления завихрителя при изменении угла установки
лопаток от 15
о
до 25°.
Аналитическое решение. Промежуточные результаты:
2
Y = 179;
2
Y
S
= 12;
2
Y
S = 6;
D
12
= 24;
2
Y
S = 11; S
D
= 8; f = 3,
t
ˆ
= 3 > t
0,025;6
= 2, 45.
Ответ. Гипотеза Н
0
(6) о независимости перепада давления завихрителя от изменения угла
установки лопаток от 15° до 25° отклоняется с уровнем значимости α < 0,05.
Графическое решение. На рис., б) изображены две не перекрывающиеся интервальные
оценки параметров
1
Y
ν
и
2
Y
ν
(194; 212) и (170; 188) (d
2
= 9), для которых справедливо D > 2d
2
.
Этим наглядно подтверждается предыдущий ответ. Согласно формуле (14), на рис., б)
изображены интервалы с доверительной вероятностью 1 - Р
≈
0,83.
Обобщим полученные выше результаты на m-мерный случай. Проверим гипотезу о
равенстве МО распределения m случайных величин Y
1
, Y
2
, … , Y
m
.
Задача 3. Пусть
{
}
mY
N
i
R
i
−
=1
независимых выборок
(
)
mR,1=
равного объема N из
множества значений
(
)
2
,~
RR
YYR
NY σν и
222
...
1
YYY
m
σσσ === . Проверить l нулевых гипотез о
равенстве пар МО распределений величин Y
1
, Y
2
, ..., Y
m
с уровнем значимости α
k
, то есть гипотезы
№ 22 [Т3Р1]
(
)
0
:;,1,;;1,
ij
nYY
Hijmijnl
νν
=∈≠=
, (15)
(
)
2/1
2
−== mmCl
m
(16)
(здесь l – число сочетаний из т по 2) против двусторонних альтернатив
1
:
ij
nYY
H
νν
≠
.
Аналитическое решение. В нашем случае дисперсии m случайных величин
(
)
1,
R
YRm
=
равны. Следовательно, оценка дисперсии
∑
=
→==
m
i
YYYY
mSS
km
1
2222
/
ˆ
σσ (17)
с числом степеней свободы mf = mN - m. Условие отклонения каждой из нулевых гипотез (15)
имеет вид [6]:

4
()
(
)
(
)
/2,
ˆ
//;,1,;;1,
nijDijD
lmf
tDSYYStijmijnl
α
==−>∈≠=. (18)
Эта же задача может быть решена графически ДИ-методом. На графике строим m
интервальных оценок центров
1
Y
ν
, … ,
m
Y
ν
:
(
)
,,1,
kmkm
YdYdkm
−+=
(19)
с размахом 2d
m
. Каждая из нулевых гипотез H
0n
(15) отклоняется, если
(
)
2;,1,;
ijijm
YYDdijmij
−=>∈≠
. (20)
Для вычисления полуразмаха d
m
комбинируем (18) и (20). Получаем
()
()
0,5
/2;
2
m
mY
lmf
dStN
α
−
= . (21)
Определим доверительную вероятность 1 - Р, соответствующую интервалу (19). Заменим
величину f в равенстве (5) на mf,
α
- на Р и S
Y
- нa
m
Y
S
. Приравнивая правые части равенств (5) и
(21), получим зависимость Р от α, m и f в неявном виде:
t
P/2,mf
= t
α/(2l);mf
•2
-0,5
. (22)
Уравнение (22) легко решается относительно доверительной вероятности 1 - Р с помощью
номограммы [рис. 4Р1]; в явном виде относительно Р уравнение (22) аппроксимируется с
помощью следующих формул:
- в области
(
)
8,2∈m
,
(
)
1,3
f∈ , α ∈ [10
-5
; 0,5] - с ошибкой не более 15%:
lgP = 0,015 + 0,14f + 0,085m + 0,984 lgα; (23)
- в области
(
)
8,2∈m ,
(
)
∞∈,4f , α ∈ [10
-5
; 0,5] - c ошибкой не более 20%:
lgP = 0,45 + 0,78 lgα. (24)
Пример 3. Даны четыре случайные нормально распределенные величины, представленные
независимыми выборками по пяти элементов в каждой. Задан критический уровень значимости
α
k
= 0,06. С какой доверительной вероятностью 1 - Р необходимо построить интервальные оценки
для четырех центров распределения этих величин, чтобы проверить методом ДИ гипотезы
n
H
0
(15) о равенстве пар МО?
Решение. Число проверяемых гипотез l = 3•4/2 = 6. Для обращения к номограмме (см. [рис.
4Р1]) найдем α' = α
k
/l = 0,01; f' = т (N - 1) = 16. По значениям α' и f' на номограмме находим
t
0,01/2;16
= 2, 92. По значениям t
Р/2;16
= 2,92•2
-0,5
= 2,065 и f' = 16, согласно уравнению (22), на
номограмме определяем P = 0,057, откуда искомая доверительная вероятность 1 – Р = 0,943.
Пример 4. К условиям примеров 1 и 2 добавим результаты измерения еще одной величины
Y
3
:
{
}
4
1
3
=i
i
Y = {142; 150; 158; 164} при Х = 35° [5]. Требуется решить задачу 3.
Промежуточные результаты аналитического решения:
3
Y = 153,5;
3
Y
S
= 9,57;
3
Y
S = 10,16;
3
Y
S = 4,78; D
12
= 24; D
13
= 49,5; D
23
= 25,5; S
D
= 6,76; f = 3;
1
ˆ
t
= 3,55 > t
0,05/6;9
= 3;
2
ˆ
t
= 7,32 > t
0,05/6;9
= 3;
3
ˆ
t
= 3,77 > t
0,05/6;9
= 3.
Ответ. Все гипотезы Н
0n
,
3,1=n
(15) о независимости перепада давления завихрителя от
изменения угла установки лопаток отклоняются с уровнем значимости α < 0,05.
Графическое решение. На рис., (в) изображены интервальные оценки (19) параметров
1
Y
ν
,
2
Y
ν
и
3
Y
ν
: (192,4; 213,6), (168,4; 189,6) и (142,9; 164,1); соответственно; d
3
= 10,6. Этот рисунок
наглядно подтверждает предыдущий ответ. Согласно уравнению (22), на рис., (в) изображены три
не перекрывающиеся ДИ с доверительной вероятностью 1 – Р = 0,93.
Интересно проследить за изменением интервальной оценки параметра
1
Y
ν
, которая для
наглядности на рис. изображена вдоль одной прямой: с увеличением числа т сравниваемых

5
параметров
i
Y
ν
при одном и том же уровне значимости α
k
доверительный интервал становится
шире.
В прикладных работах часто встречаются изображения «традиционных» 95%-ных ДИ
(1 – P = 0,95). Если по этим изображениям нужно проверить гипотезы (15), то следует учитывать,
что, согласно уравнению (22), при значениях f, больших 20, получаем α
k
≈
0,0028 т (т—1), то
есть критический уровень значимости α
k
зависит от т так:
m 2 3 4 5 6 7 8 и так далее
α
k
0,0056 0,017 0,034 0,056 0,084 0,12 0,16 и так далее
Литература
1. Цейтлин Н. А. Основные требования к уравнениям регрессии, предназначенным для использования
на ЭЦВМ: - Харьков, 1974. - 77 с. - Рукопись НИОХИМ. Деп. в ОНИИТЭХИМ: г. Черкассы 05.04.74, №
198/74 деп.
2. Цейтлин Н. А. Простые статистические методы обработки результатов наблюдений на газоочистных
установках. - Харьков, 1979. - 10 с. - Рукопись НИОХИМ. Деп. в ОНИИТЭХИМ г. Черкассы 25.06.79, №
2815/79 деп.
3. Справочник по надежности. Т. 1 /Под ред. Б. Р. Левина. - М.: Мир, 1969. - 340 с.
4. Boyd W. C. A Nomogram for the Student-Fisher t-test. - Am. Stat Ass. Journ., 1969, №64, p. 1664 - 1667.
5. Гурьев В. С., Успенский В. А. Результаты экспериментального исследования вихревого
пылеуловителя. - Промышленная и санитарная очистка газов, 1975, № 4, с. 12 – 14.
6. Fisher R. М. The Design of experiments. London, Oliver and Boyd. – 1935. - 360 p.
1
1.2.2. Попарное сравнение среднеквадратичных отклонений распределений
случайных величин методом доверительных интервалов
Какая разница между любовником и мужем? - В среднем - двадцать минут.
Материал настоящего раздела обсуждался с двумя рецензентами. Один был «чёрным»,
другой – доброжелательным, но принципиальным.
Итак, начнём по порядку. 14-го декабря 1987-го года в редакцию журнала «Измерительная
техника» была направлена одноимённая рукопись автора.
Мерой случайного разброса результатов измерения технического параметра (температуры,
давления, концентрации и т. п.) является среднеквадратичное отклонение (СО).
Точное значение СО σ
Y
обычно не известно, а по N результатам измерений могут быть
получены приближенные оценки - точечная (однозначная) S
Y
с f = N - 1 степенями свободы и
интервальная (S
HY
, S
BY
), где S
HY
и S
BY
- нижняя и верхняя границы доверительного интервала
(ДИ). (ДИ с заранее заданной доверительной вероятностью 1 - P накрывает неизвестное точное
значение СО σ
Y
[1].).
Обычно ДИ приводятся и для наглядности изображаются на графике только для того, чтобы
проиллюстрировать погрешности измерений [1]. Между тем наглядность и информативность
статистической обработки результатов наблюдений можно повысить, если одновременно с
интервальным оцениванием выполнять проверку статистических гипотез методом доверительных
интервалов (МДИ) [3].
Для этого необходимо строить ДИ так, чтобы можно было с заданным критическим уровнем
значимости
α
к
проверять сформулированные гипотезы. Величина доверительной вероятности в
таких построениях играет вспомогательную роль и в случае необходимости может быть
вычислена [3].
В работе [3] (и [Р1.2.1]) МДИ был использован для попарного сравнения нескольких
математических ожиданий нормально распределенных случайных величин с одинаковыми СО.
В настоящем работе МДИ получил дальнейшее развитие в приложении для попарного
сравнения различных СО погрешностей измерения параметра физического свойства,
распределенного по нормальному закону.
Опишем сначала процедуру интервального оценивания СО.
Задача 1. Пусть
{
}
N
i
i
Y
1=
- выборка объемом N элементов из бесконечного множества
значений случайной величины Y, распределенной по нормальному закону с центром ν
Y
и СО σ
Y
,
или в краткой записи Y ~ N(ν
Y
,
σ
Y
); задана доверительная вероятность 1 - P.
Необходимо получить две оценки СО σ
Y
: а) точечную и б) двустороннюю равновероятную
интервальную.
Решение.
а) Точечная оценка СО S
Y
вычисляется по формуле [Ф(33)Р1].
Пример 1. Лаборант А выполнил три замера массовой концентрации магния в растворе
бикарбоната магния:
{
}
3
1
1
=i
i
Y = {5,433; 5,402; 5,367} г/л [2]. Найти точечную оценку СО
погрешностки измерения
σ
1Y
.
Решение. По формуле (1) нашли S
1Y
= 0,034 г/л с f = 2-мя степенями свободы (точка на рис. 1a).
Замечание. Статистика S
Y
является смещенной (на величину d
S
= S
Y
/(4f) [4, c. 230]) оценкой СО
σ
Y
. Однако в практических расчетах смещение d
S
не учитывается по следующим причинам:
величина d
S
не превышает СО S
S
= S
Y
/(2N)
0,5
ошибки величины S
Y
; при любых f
≥
1 [5, c. 207]; при
увеличении f смещение d
S
быстро уменьшается; величина d
S
изменяет цифры, которые
отбрасываются при округлении оценки S
Y
[6, с. 210; Р3.8].

2
Рис. 1. Статистические оценивание и проверка гипотез относительно среднеквадратичных
отклонений (СО) случайных шибок измерения массовой концентрации магния в растворе
бикарбоната магния методом доверительных интервалов (ДИ):
а) 95%-ный ДИ для
σ
1Y
(см. примеры 1, 2); б) два 87%-ных ДИ для проверки гипотезы (5) о равенстве СО
σ
1Y
=
σ
2
Y
(см. пример 3); в) три 93,3%-ных ДИ для проверки гипотез (23) о равенстве СО
σ
1
Y
=
σ
2
Y
,
σ
1
Y
=
σ
3
Y
,
σ
2
Y
=
σ
3Y
(см. пример 4); S
Y
- СО, г/л S
1Y
, S
2Y
, S
3Y
– CO, полученные по результатам наблюдений, выполненных
лаборантами А, Б и В соответственно;
∆
iH
,
∆
iB
- нижние и верхние плечи ДИ; Q
ij
- расстояния между
значениями S
iY
и S
jY
.
б) Для интервального оценивания СО
σ
Y
(а в дальнейшем – и для проверки гипотез) вместо
обычно используемой статистики хи-квадрат
2
f
χ с f степенями свободы [1, с. 153], будем
использовать статистику Фишера
21
, ff
F с числами степеней свободы f
1
- числителя и f
2
-
знаменателя [7, c. 12].
Следуя Шеффе [8, с. 39], определим верхний
α
-предел распределения Фишера
α,,
21
ff
F как
число, такое, что
(
)
α
α
=>
,,,
2121
ffff
FFP, где Р(⋅) - вероятность; α - уровень значимости.
Определить значения величины
α,,
21
ff
F по заданным числам степеней свободы f
1
, f
1
и
значению
α
(или, наоборот - определить значение
α
- по заданным f
1
, f
2
и
α,,
21
ff
F ) можно с
помощью таблиц [1, с. 296], [5, с. 472], простых аппроксимаций [7, с. 13; Р1.1.7.1], или сложных
формул [9, с. 437; Р1.2.4.7], а также номограммы [рис. 5Р1].
Воспользуемся тем, что статистика
22
YY
S σ
имеет распределение Фишера с f
1
= f и f
2
=
∞
степенями свободы (
∞
=
,
22
fYY
FS σ ) [1] и для него легко построить границы двустороннего
доверительного интервала - нижнюю F
f,
∞
, 1-
λ
(вероятность 1 - λ ≥ 0,5) и верхнюю F
f,
∞
,
γ
(вероятность
γ
≤
0,5) так что
Р(F
f, ∞, 1-λ
≤ F
f, ∞
=
22
YY
S σ ≤ F
f, ∞, γ
) = 1 - Р. (1)
Поскольку по условию задачи 1 – P = 1 –(
λ
+
γ
), а вероятности
λ
и
γ
равны, то
λ
=
γ
= P/2.
Заменим в соотношении (1), согласно равенству [Ф(22)Р1], предел F
f, ∞, 1-λ
на 1/F
∞, f,λ
и
перепишем его окончательно так:
(
)
PFSSFSSP
PfYBYYPfYHY
−==≤≤=
∞∞
1
5,0
2/,,
5,0
2/,,
σ
, (2)
где S
HY
и S
BY
- равновероятные, соответственно, нижняя и верхняя 100(1 - Р)%-ные границы
доверительного интервала для σ
Y
.
Для графического представления ДИ СО рекомендуется использовать «логарифмическую
бумагу», на которой отношению величин соответствует разность их логарифмов. Это позволяет
3
выделить в ДИ два неравных плеча (см. рис. 1a) - верхнее Δ
1В
= lgS
BY
- lgS
Y
и нижнее Δ
1H
= lgS
Y
–
lgS
HY
. Из выражения (2) следует, что
Δ
1В
= 0,5lgF
∞,f,P/2
; Δ
1H
= 0,5lgF
f,∞,P/2
. (3)
Пример 2. По данным примера 1 построить двустороннюю равновероятную интервальную
оценку СО σ
Y
с доверительной вероятностью 1 - P = 0,95.
Решение. Воспользуемся простыми аппроксимациями [7, с. 13; Ф(27)Р1]
F
2,∞,P/2
= -ln(P/2) и F
∞,2,P/2
= -1/ln(1 – P/2). (4)
Получим F
2;∞;0,025
≈ 3,69; F
∞;2;0,025
≈ 39,5 (см. также номограмму [рис. 5Р1]). Теперь по
формулам (2) S
1HY
= 0,034/3,69
0,5
= 0,018 г/л; S
1BY
= 0,034*39,5
0,5
= 0,21 г/л.
Ответ: Р(0,018 ≤ σ
Y
≤ 0,21 г/л) = 0,95. Построенная 95%-ная доверительная область
выделена жирной линией в скобках на рис. 1a.
Сформулируем задачу проверки гипотез о равенстве СО двух величин Y
1
и Y
2
.
Задача 2. Пусть
{
}
Nu
i
iu
Y
1=
- две независимые выборки (
2,1=u
) разного объема (N
1
≠
N
2
) из
множества значений Y
u
~ N(
ν
u
,
σ
uY
).
Проверить с уровнем значимости
α
=
α
к
гипотезу о равенстве СО
H
0
: σ
1Y
= σ
2Y
(5)
против альтернативы H
1
:
σ
1Y
≠
σ
2Y
.
Аналитическое решение. Воспользуемся тем, что статистика
(
)
2
1
2
2
2
2
2
1YYYY
SSσσ имеет
распределение Фишера с f
1
и f
2
степенями свободы. По формуле [Ф(33)Р1] вычислим S
uY
( 2,1=u ).
Условие отклонения гипотезы (5) имеет вид [7, c. 8]
(
)
(
)
2
2
2
1
2
2
2
1,2/,,
,min/,max
ˆ
33
YYYYffff
SSSSFF
HrHr
=<
α
, (6)
где f
r
и f
3H
- числа степеней свободы числителя и знаменателя F-отношения, соответственно;
f
r
= f
1
и f
3H
= f
2
, если S
1Y
> S
2Y
, или f
r
= f
2
и f
3H
= f
1
, если S
1Y
< S
2Y
.
Критическое значение статистики Фишера
2/,,
3
α
Hr
ff
F определяется по заданным f
r
, f
3H
и α
к
/2.
Графическое решение методом ДИ. На графике строим два ДИ оценки СО
σ
1Y
и
σ
2Y
:
(lgS
uY
- ∆
2H
, lgS
uY
+ ∆
2B
);
2,1=u
, (7)
где
∆
2H
и
∆
2B
- нижнее и верхнее плечи ДИ, построенные с помощью формул (3) так, чтобы
на заданном уровне значимости α = α
к
условие отклонения гипотезы Н
0
(5) имело вид
lgS
1Y
– lgS
2Y
= Q
12
>
∆
2H
+
∆
2B
при S
1Y
> S
2Y
(8)
или lgS
2Y
- lgS
1Y
= Q
21
>
∆
2H
+
∆
2B
при S
1Y
< S
2Y
. (9)
Определим доверительную вероятность 1 - P, которой соответствуют доверительные
интервалы (7). Пусть для определенности S
1Y
> S
2Y
. Заменим знаки неравенств в выражениях (6) и
(8) на знаки равенства. Полученное равенство (6) позволяет заменить левую часть полученного
равенства (8) lgS
1Y
– lgS
2Y
на 0,5
2/,,
21
αff
F ; равенства (3) позволяют заменить правую часть
равенства (8) на 0,5(
2/,,2/,,
21
lglg
PfPf
FF
∞∞
+ ). После элементарных преобразований полученного
равенства приходим к зависимости 1 - Р от
α
, f
1
и f
2
в неявном виде:
2/,,2/,,2/,,
2121
PfPfff
FFF
∞∞
=
α
. (10)
Для решения уравнения (10) относительно 1 - Р можно, например, с помощью номограммы
[рис. 5Р1] построить график функции
α
=
α
(f
1
, f
2
, P) в координатах lg
α
- lgP, а затем по значениям
f
1
, f
2
и α определить 1 - P. Уравнение (10) можно решить относительно α в явном виде с помощью
известных аппроксимаций обратной функции распределения Фишера [7, с. 13; Ф(19)Р1 и (21)Р1].
Так, при 1
≤
2/,,
21
αff
F
≤
10, f
1
≥
3 и f
2
≥
3 получаем:
α = 1 – [1 – exp(h
2
2/α
Z )]
0,5
sgnZ
α/2
; h = - 0,6118; (11)
()
1212
2
21/32/3
/2,,/2,,/2
11()
ffff
ZFbabFa
ααα
=−−++
; (12)
12
,,/2
ff
F
α
= {
()()
()
1
2
0,50,52
/2/2/2
111
PPP
aZabZbbbZ
−
−+−+−−
}
3
(13)
где Z
P/2
= 1,94[-lg(2P – P
2
)]
0,5
; a = 2/(9f
1
); b = 2/(9f
2
).
При f
1
= f
2
= f
≥
3 вместо формул (12) и (13) можно использовать формулы:
Z
α
/2
= L -[L
2
- 2t
f,
α
/2
(f + 3)]
0,5
; (14)
4
L = f + 3 + 1,5t
f,
α
/2
; c = 2/(9f); (15)
t
f,α/2
= 0,5[(F
f,f,α/2
+ F
-1
f,f,α/2
- 2)f]
0,5
; (16)
F
f,f,α/2
= [(1 – c + Z
P/2
c
0,5
)/(1 – c - c
0,5
Z
P/2
)]
3
. (I7)
При значениях f
1
и f
2
, равных 1 или 2, уравнение (10) решается относительно
α
еще проще:
α
= 2 – 1,2732 arc tg
5,0
2/,1,1 α
F ;
α
= 2/(F
2,2,α/2
+ 1); (18)
α = 2 – 2/(1 + 2/F
1,2,
α
/2
)
0,5
; α = 2/(2F
2,1,
α
/2
+ 1)
0,5
; (19)
сомножители в правой части равенства (10) аппроксимируются формулами (4), а также
F
1,∞,P/2
= hln(P – P
2
/4); F
∞,1,P/2
= hln(1 – P
2
/4); h = - 0,6118. (20)
На практике чаще всего используются СО с равными числами степеней свободы. Поэтому с
помощью аппроксимаций (11), (14) - (18), (4) и (19) построены номограмма (рис. 2), одна
аппроксимация
P = 0,975
α
0,715
f
0,138
; V
P
= 14% (21)
(где V
P
- относительная погрешность величины P) и другая более точная аппроксимация
lgP = 0,1175 + 0,8169lg
α
+ 0,0247lgf – 0,1654(lg
α
)lgf – 0,0932(lgf)
2
; V
P
= 5%. (22)
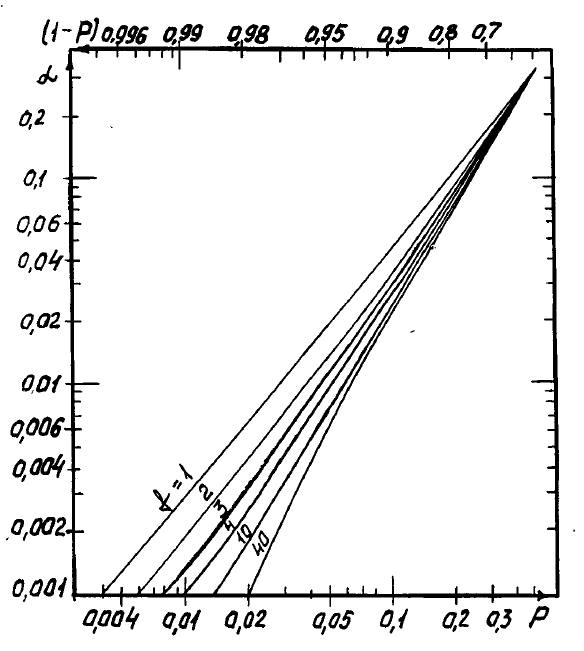
Pис. 2. Номограмма для определения доверительной вероятности 1 - Ρ по заданному уровню
значимости α и числу степеней свободы f (при сравнении среднеквадратичных отклонений).
Пример 3. Лаборант Б выполнил три замера массовой концентрации магния, по результатам
которых получена оценка СО S
2Y
= 0,003 г/л [2]. Необходимо сравнить случайные погрешности
результатов измерений, выполненных лаборантами А (см. пример 1) и Б на уровне значимости
α
к
= 0,05, то есть решить задачу 2.
Аналитическое решение. По второй из формул (18) определим критическое значение
статистики Фишера F
2,2,α/2
= 2/
α
- 1 = 39. (Это же значение находим по номограмме [рис. 5Р1] при
α
=
α
к
/2 = 0,025 и f
1
= f
2
= 2). Согласно выражению (6) 39 < (0,034/0,003)
2
= 128 =
2,2
ˆ
F .
Ответ. Гипотеза (5) о равенстве СО случайных погрешностей измерений, выполненных
лаборантами А и Б отклоняется с уровнем значимости
α
< 0,05.

5
Графическое решение методом ДИ. Определим доверительную вероятность 1 – Р. По
формуле (21) P = 0,126. Похожие результаты дает формула (22) (P = 0,131) и номограмма [рис.
5Р1] (P = 0,13). Для проверки последнего результата воспользуемся точными формулами (4), (10)
и (18). Получим F
2;∞;0,065
= 2,73; F
∞;2;0,065
= 14,88; F
2;2;α/2
= 40,62;
α
= 0,048. Погрешность 4% по
сравнению c α
к
= 0,05 удовлетворительная.
Итак, 1 - P = 0,87. По формулам (2) находим 4 границы двух ДИ: S
1HY
= 0,034/2,73
0,5
= 0,0206
г/л; S
1BY
= 0,034
⋅
14,88
0,5
= 0,131 г/л; S
2HY
= 0,0018 г/л; S
2BY
= 0,0116 г/л.
Изображение на рис. 1б) двух не перекрывающихся ДИ подтверждает справедливость
неравенства (8). Этим наглядно иллюстрируется предыдущий ответ.
Обобщим
полученные выше результаты
на многомерный случай
. Сформулируем
задачу
попарного сравнения СО случайных величин Y
1
, Y
2
, …, Y
m
, m ≥ 2.
Задача 3. Пусть
{
}
u
N
i
iu
Y
1=
- m независимых выборок (
mu ,1=
) разного объема N
u
из множества
значений Y
u
~ N(V
u
, σ
uY
).
Проверить (с уровнем значимости
α
=
α
к
) l нулевых гипотез № 20 [Т3Р1] о равенстве СО
σ
uY
H
n0
:
σ
iY
=
σ
jY
, 1
≤
i < j
≤
m;
ln ,1=
, (23)
(где l - число сравниваемых nap CO, равное числу проверяемых гипотез, l =
2
m
C
= т(т - 1)/2)
против l двусторонних альтернатив H
n1
:
σ
iY
≠
σ
jY
.
Аналитическое решение. Для проверки гипотез (23) воспользуемся статистикой Фишера-
Бонферрони
()
lff
Hr
F
2/,,
3
α
[Ф(51)Р1], предложенной автором в работе [7, c. 8]. Для пар СО S
iY
и S
jY
,
имеющих приблизительно равные числа степеней свободы f
i
и f
j
справедливо условие отклонения
нулевой гипотезы (23):
()
{
}
{
}
2222
,2/,,
,min,max
ˆ
33
jYiYjYiYfijflff
SSSSFF
HrHr
=<
α
, (24)
где f
r
= f
i
и f
3H
= f
j
, если S
iY
> S
jY
, или f
r
= f
j
и f
3H
= f
i
, если S
iY
< S
jY
.
Критическое значение статистики Фишера
()
lff
Hr
F
2/,,
3
α
определяется по заданным f
1
= f
r
, f
2
=
f
3H
и
α
=
α
к
/(2l) =
α
к
/[m(m – 1)].
В общем случае задача 3 не может быть решена методом ДИ, потому что необходимо
сравнить СО S
iY
и S
jY
с разными числами степеней свободы f
i
≠ f
j
. А для любой такой пары
необходимо строить пары ДИ с разными плечами. Задача 3 имеет решение только в случае равных
чисел степеней свободы f
u
= f (
mu ,1=
).
Графическое решение методом ДИ. На графике строят m интервальных оценок СО (7).
Условие отклонения гипотезы H
и0
(23) имеет вид (8) или (9), причем в выражениях (8) и (9)
индексы 1 и 2 заменяются индексами i и j (1
≤
i < j
≤
т). Другими словами, для попарного
сравнения т CO методом ДИ нулевые гипотезы о равенстве СО σ
iY
и σ
jY
отклоняются в
случае, если соответствующие доверительные интервалы (7) для этих СО не перекрываются.
Чтобы определить доверительную вероятность, которой соответствуют ДИ (7), необходимо
решить уравнение
F
f,f,
α
/(2l)
= F
f,
∞
,P/2
⋅F
∞
,f,P/2
(25)
относительно 1 - Р. Это уравнение получено точно так же, как и уравнение (10), но отличается, от
него лишь переменной l. Для решения уравнения (25) относительно 1 - Р можно воспользоваться
решением уравнения (10), если в уравнении (25) заменить величину α
к
/l на
α
′
.
Пример 4.
Лаборант В выполнил три замера массовой концентрации магния; получено СО
S
3Y
= 0,006 г/л [2].
Необходимо сравнить СО погрешностей, полученных по данным лаборантов А, Б и В (см.
примеры 1 - 3) на уровне значимости α
к
= 0,06, то есть решить задачу 3 для случая т = 3.
Аналитическое решение
. Число проверяемых гипотез (23) равно l = 3(3 - 1)/2 = 3. Заменим
α
к
/l на
α
′
= 0,06/3 = 0,02 и по второй из формул (18) определим F
2,2,
α
’/2
= 2/0,02 - 1 = 99 (по
номограмме [рис. 5Р1]: f
1
= f
2
= 2 и
α
=
α
к
/(2l) = 0,01; находим F
2,2,α/(2l)
≈
100). По формуле (24)
сравниваем S
1Y
и S
2Y
:
99 <
{
}
{
}
2
2
2
1
2
2
2
1
,min/,max
YYYY
SSSS
= 0,034
2
/0,003
2
= 128; S
1Y
и S
3Y
: 99 > 0,034
2
/0,006
2
= 32; S
2Y
и
S
3Y
: 99 > 0,006
2
/0,003
2
= 4.

6
Ответ. Гипотеза (23) о равенстве СО случайных погрешностей измерения, выполненных
лаборантами А и Б (
σ
1Y
и
σ
2Y
), отклоняется (
α
< 0,06), а выполненных лаборантами А и В (
σ
1Y
и
σ
3Y
) или Б и В (
σ
2Y
и
σ
3Y
) - не отклоняется.
Графическое решение методом ДИ. Определим 1 – Р. Заменим в формуле (25)
α
к
/l на
α
′
= 0,02. По формуле (21) P = 0,065; по (22) P = 0,065; по рис. 2 P = 0,067.
Проконтролируем последний результат. По (4): F
2;∞;0,0335
= 3,40; F
∞;2;0,0335
= 29,35; по (10):
F
2,2,α/2
= 99,78; по второй формуле (18):
α
′
= 0,0198, почти равное заданному
α
′
= 0,02.
Итак, 1 - Р = 0,933. По формулам (2) находим 6 границ трех ДИ: S
1HY
= 0,034/3,4
0,5
= 0,018;
S
1BY
= 0,034⋅29,35
0,5
= 0,18; S
2HY
= 0,0016; S
2BY
= 0,016; S
3HY
= 0,0033; S
3BY
= 0,033.
Изображение полученных ДИ на рис. 1в) подтверждает справедливость неравенства (8) для
случаев А и Б и не подтверждает - для А и В, а также для Б и В. Этим наглядно иллюстрируется
предыдущий ответ.
Интересно проследить за изменением интервальной оценки параметра
σ
1Y
, которая для
наглядности на рис. 1 изображена вдоль одной прямой: с увеличением числа т сравниваемых
параметров σ
iY
при почти одном и том же уровне значимости α
к
ДИ становится шире.
В прикладных работах могут встретиться изображения традиционных 95%-ных ДИ
(1 – Ρ = 0,95). Если по этим изображениям нужно проверить гипотезы (23), то соответствующий
критический уровень значимости
α
к
, на котором происходит эта проверка, легко определить по
формуле (10).
Пример 5. Пусть по данным примеров 1 - 4 исследователь построил три 95%-ных ДИ для
σ
iY
(
3,1=i
). На каком уровне значимости
α
к
выполняется проверка гипотез (23) методом ДИ?
Решение. Для построения 95%-ного ДИ исследователь должен был определить по (4):
F
2;∞;0,05/2
= 3,69 и F
∞;2;0,025
= 39,5. Согласно (10) F
2,2,α/2
= 145,76; по второй формуле (18) получаем
ответ: α
к
= 0,014.
Литература
1. Справочник по надежности / Пер. с англ. Ю. Г. Епишеина и Б. А. Смиренина. Под ред. Б. Р. Левина. - T.
1. - M.: Мир, 1969. - 340 с.
2. Самойленко В. И., Цейтлин H. А. Использование статистических методов при исследовании процесса
карбонизации гидроокиси магния. / Технология соды и содопродуктов /Под ред. Э. К. Беляева и Н. С.
Старчикова: Труды/НИОХИМ. – Т. 52. - Харьков, Ι980. – С. 9 – 17.
3. Цейтлин Н. А. Проверка гипотез методов доверительных интервалов // Методы математической
статистики в химии /Под ред. Н. А. Цейтлина: Труды/НИОХИМ. – Т. 53. - Харьков, 1981. – С. 82 – 89.
4. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. - M.: Прогресс, 1976.- 496 с.
5. Смирнов H. В., Дунин-Барковский И. В. Курс теории вероятностей и математической статистики для
технических приложений. – М.: Наука, 1965. – 512 с.
6. Бурдун Г. Д., Марков Б. Н. Основы метрологии. - M.: Изд. стандартов, 1975. – 336 с.
7. Цейтлин Н. А. Применение методов математической теории эксперимента в содовой промышленности /
Обзорная информация. Сер. Содовая промышленность. – М.: НИИТЭХИМ, 1984. – 48с.
8. Шеффе Г. Дисперсионный анализ. – M.: Наука, 1980. - 512 с.
9. Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика // Основы моделирования и
первичная обработка данных. – M.: Финансы и статистика, 1983. - 472 с.
10. Василенко А. Н., Герасимович Т. А., Горячева Т. В. и др. Математическое обеспечение ЕС ЭВМ. –
Вып. 14. - Минск: Ин-т математики АН БССР, 1978. - 330 с.
11. Себер Дж. Линейный регрессионный анализ. - М.: Мир, 1980. - 456 с.
12. Большев Л. H., Смирнов H. В. Таблицы математической статистики. - M.: Наука, 1965. - 464 с.
13. Dunn O. J., J. Am. Stat. Assoc., p. 52-64.
14. Miller R. G. Jr. Simultaneous Statistical Inference. Mc Graw. Hill, New York, 1966.
15. Fischer R. The Design of experiments Oliver and Boyd. Zandov, 1935. Dayton C. M., Schater N. D., J. Am.
Stat. Assoc., 68., p. 78-83.
16. Грекова И. Вопросы философии. № 6, 1976, с. 104-114.
17. Закс Л. Статистическое оценивание. - M.: Статистика, 1976. - 600 с.
1
1.2.3. Дискуссия с официальными рецензентами
Через семь месяцев (как это принято в больших журналах) на статью пришёл ответ от
заместителя главного редактора с копией отзыва «чёрного» рецензента.
РЕЦЕНЗИЯ на статью H. А. Цейтлина «Попарное сравнение…»
Данная статья посвящена одной из распространенных статистических задач - сравнению
дисперсий нескольких выборок.
Однако изложенный материал вызывает ряд существенных замечаний.
1. Прикладная (метрологическая) постановка задачи недостаточно обоснована. Автор не
дает содержательной постановки метрологической задачи (с. 1), не раскрывает специфики
решаемой им задачи в сравнении с другими работами по данному вопросу.
2. Неудовлетворительна также математическая постановка задачи (с. 1-2). Не показано, как
понимается совместная проверка l нулевых гипотез Н
оп
(против соответствующих альтернатив). В
частности, не ясно, как это соотносится с проверкой гипотезы о равенстве всех СО.
3. Нечеткая постановка задачи сопровождается также нечетким изложением предлагаемого
решения задачи. В частности, оказывается необоснованным переход от случая m = 2 к общему
случаю m > 2.
4. Отсутствуют ссылки на современные работы по этому вопросу, хотя задача проверки
равенства CO нескольких выборок довольно широко исследуется.
Кроме ссылки на старую работу [3], относящуюся к 1956 г., автор ссылается лишь на свои
работы, опубликованные в узкоотраслевых изданиях.
Таким образом, данную статью нельзя рекомендовать к опубликованию в журнале
«Измерительная техника».
Подпись рецензента отсутствует; копия верна. Зам. главного редактора …
По-видимому, научная статья - как революция, о которой главный большевик сказал, что
она «только тогда чего-нибудь да стоит, когда умеет себя защищать»!
ОТВЕТ на РЕЦЕНЗИЮ (печатается с купюрами)
Уважаемый заместитель главного редактора! … К сожалению, сомнения рецензента мне не
понятны. Разберем по пунктам:
1. Прикладная постановка задачи здесь настолько тривиальна, что её можно найти в любой
книге по статистике. Никакой «специфики» в постановке нет.
2. Совместная проверка l нулевых гипотез понимается прямо так, как написано в статье.
3. Обоснование перехода от случая m = 2 к общему случаю m > 2 просто. В работе написано:
«уравнение (12) получено точно так же, как и (10)». Значит, надо прочитать вывод уравнения (10)
и заменить в нём α на α/l.
4. Автору не известны современные решения данной задачи методом ДИ. Если рецензенту
они известны, то неотразимым аргументом была бы его ссылка на работу, где данная задача так же
решена. Вместо этого рецензент неопределенно пишет: «задача довольно широко исследуется».
Таким образом, я не вижу оснований, на которых моя работа не рекомендована к
публикации.
Общие замечания. Уважаемый зам. Главного редактора! … Вы дважды возвращали мою
работу на сокращение. Это явилось для работы прокрустовым ложе. Меньше будет работа –
ничего требуемое рецензентом в ней не скажешь, больше работа - нарушишь регламент. В итоге
работе отсекли важные части, на отсутствие которых даже рецензент обратил внимание. Я бы мог
переписать из учебника «достаточное» обоснование задачи, проанализировать известные решения
задачи, которые нас не устраивают. Отсечена, наконец, номограмма распределения Фишера,
которая (рецензент не даст мне соврать) широким образом может использоваться в статистике.
Должен сказать, что мои работы не впервые публикуются в научных журналах (в том числе
в Заводской лаборатории, ЖПХ, ТОХТ, «Изв. ВУЗов», ДАН УССР, ЖНХ и др.) Свои работы я
готовлю достаточно тщательно. Только за новизну идей мне отвечать трудно, так как в мире
очень много подобных публикаций. В среднем, в одном из семи случаев я получаю от редакций
отказы на публикацию. Но они бывают обстоятельно
обоснованы
. В Ваш журнал я направил
работу впервые и получил отказ, на мой взгляд, необоснованный.
