Цейтлин М.Б., Кац А.М. Лампа с бегущей волной

Подождите немного. Документ загружается.

ляются оптимальными для получения высоких к. п. Да

в изохронной ЛБВ.

При больших значениях параметра пространствен^

ного заряда (q> 1,7) введение изохронности приводив

к уменьшению к. п. д. Анализируя процесс группировки

электронов (фазовые траектории) при большом про!

странственном заряде, можно объяснить уменьшение!

к. п. д. для большого параметра пространственного за|

чШ

го

о 0,5 1,0 1

5 2,0 2,5 £

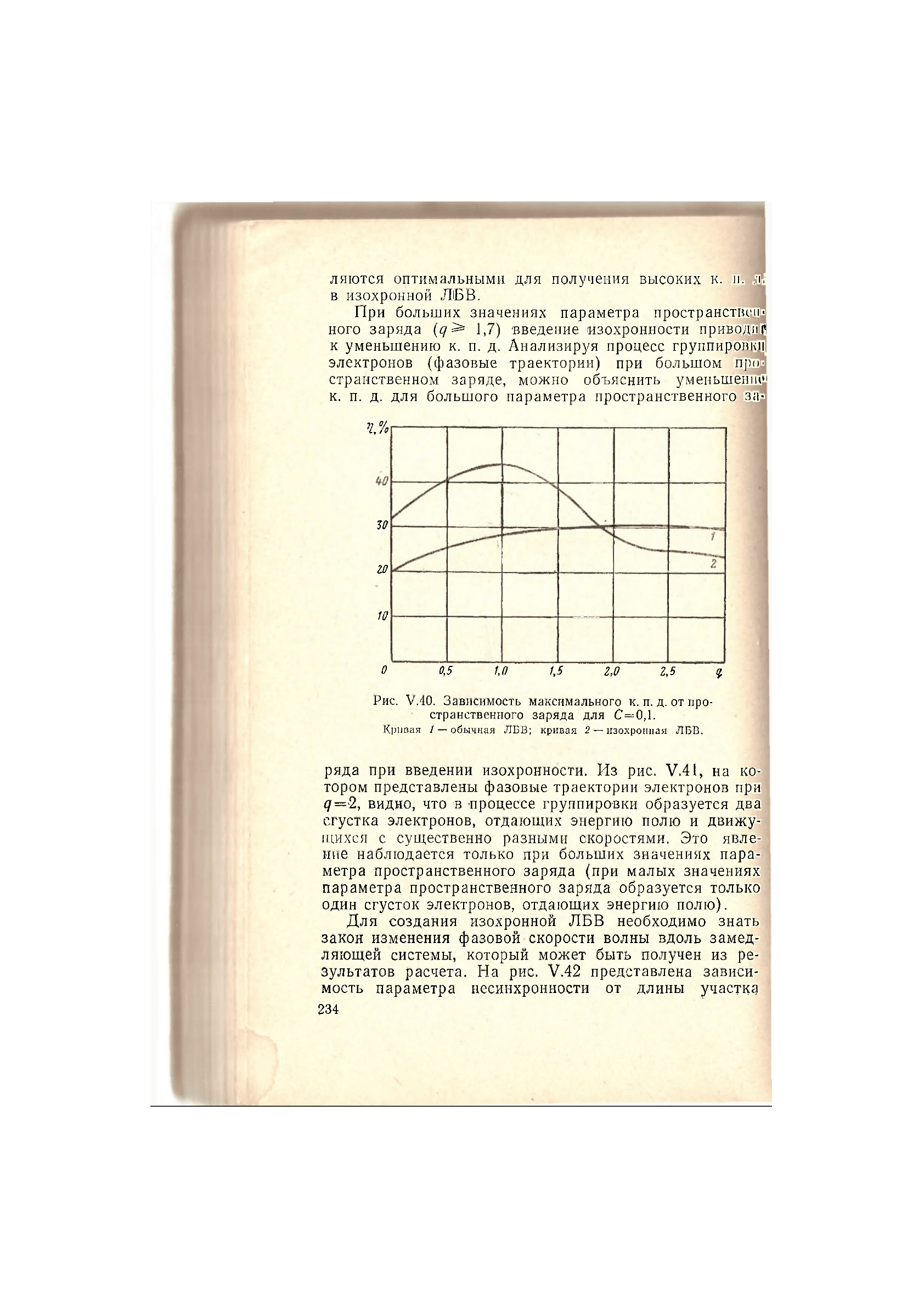
Рис. V.40. Зависимость максимального к. п. д. от про-

странственного заряда для С=0,1.

Кривая 1

—

обычная ЛБВ; кривая 2

—

изохронная ЛБВ.

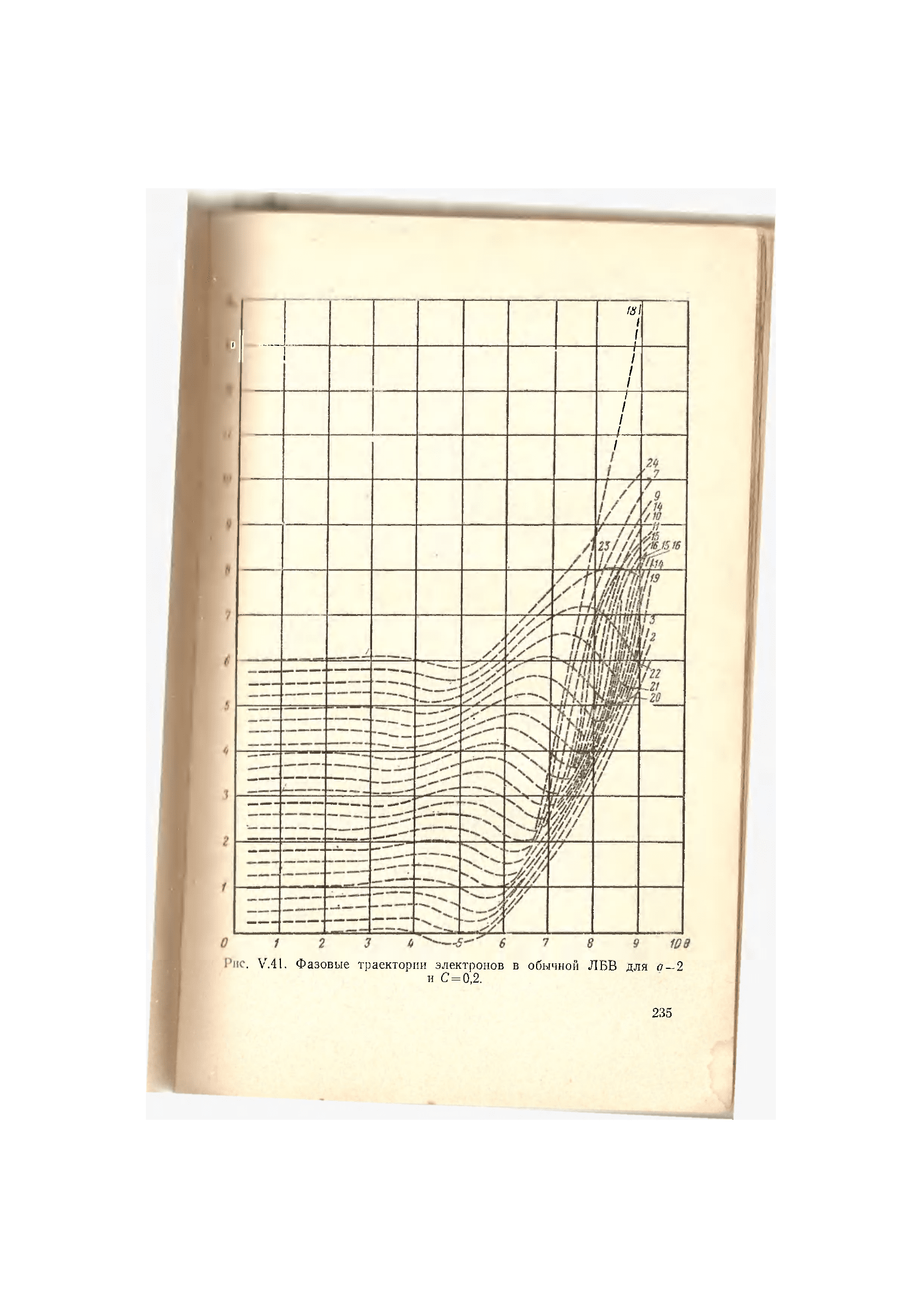
ряда при введении изохронности. Из рис. V.41, на ко-

тором представлены фазовые траектории электронов при

(7=2, видно, что в -процессе группировки образуется два

сгустка электронов, отдающих энергию полю и движу-

щихся с существенно разными скоростями. Это явле-

ние наблюдается только при больших значениях пара-

метра пространственного заряда (при малых значениях

параметра пространственного заряда образуется только

один сгусток электронов, отдающих энергию полю).

Для создания изохронной ЛБВ необходимо знать

закон изменения фазовой скорости волны вдоль замед-

ляющей системы, который может быть получен из ре-

зультатов расчета. На рис. V.42 представлена зависи-'

мость параметра несинхронности от длины участи

234

/81

—

4—

. V.4L Фазовые траектории электронов в обычной ЛБВ для а—2

и С=0,2.

.235

взаимодействия для различных значений параметра про*

странственного заряда -при С—0,1. Воспользовавшись

кривыми на рис. V.42, можно построить зависимость фа-<

Рис. V.42. Зависимость параметра несинхроииости от

длины участка взаимодействия, С=0,1.

зовой скорости волны от длины замедляющей системы.

Из определения параметра несинхронности следует

R * \ t

r > (V.30)

Уф 1+Ь

где Уф

— значение фазовой скорости волны на входе.

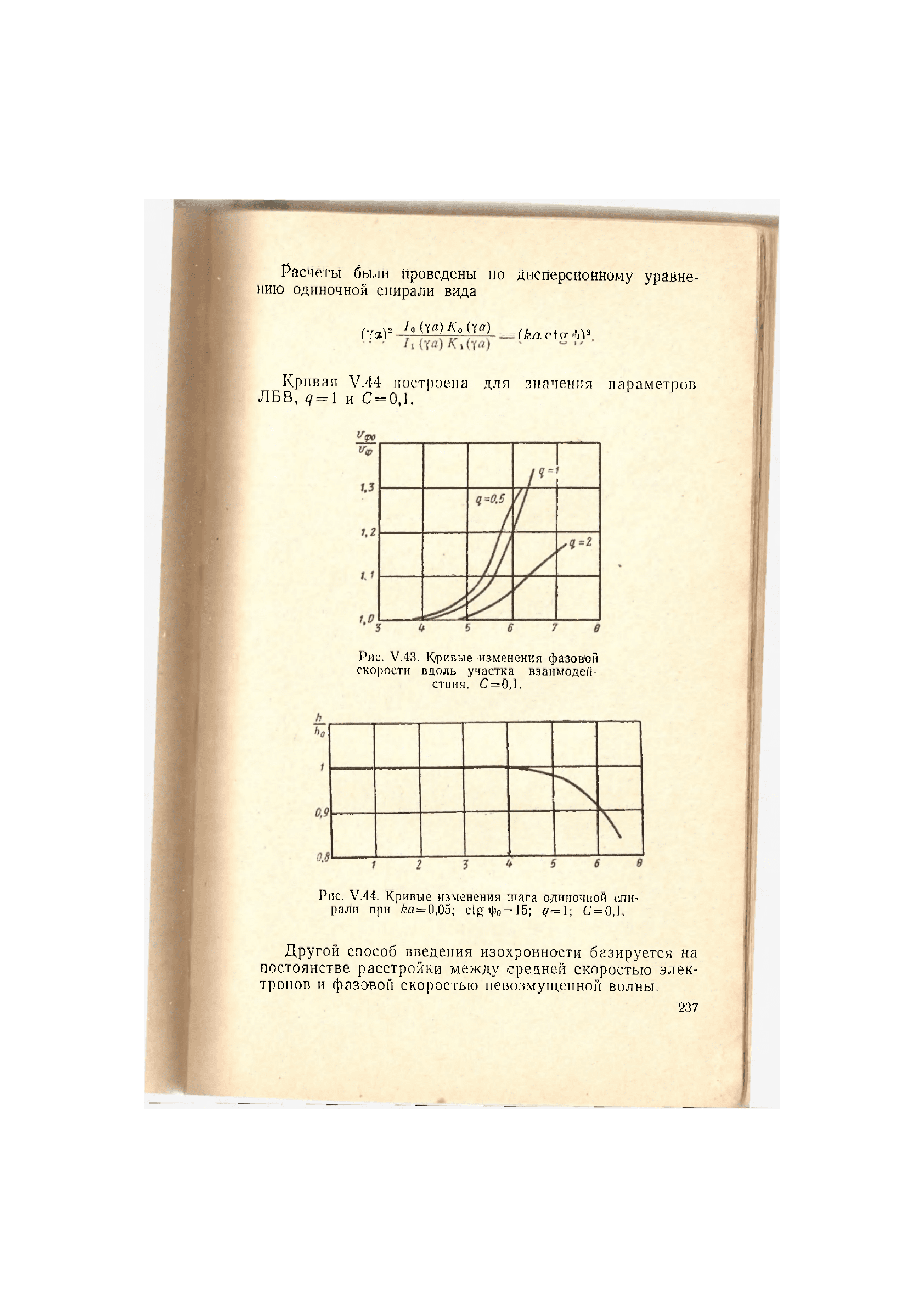
На рис. V.43 представлена зависимость отношения —

от длины участка взаимодействия. Конец каждой кривой

соответствует режиму насыщения. Из этих кривых сле-

дует, что на большей части длины системы фазовая ско-

рость должна оставаться постоянной. Наибольшее изме-

нение фазовой скорости соответствует наибольшей дости-

жимой мощности изохронной ЛБВ.

Приведенные кривые изменения фазовой скорости по-

зволяют определить изменение параметров (в основном

шага) замедляющей системы для обеспечения изохронного

режима ЛБВ. На рис. V.44 представлена зависимость шага

одиночной спирали с параметрами /га = 0,05 и ctg^

2 па

л с

=-т- = 1о от длины спирали.

.236

Расчеты былй проведены по дисперсйоййому урабйе-

нию одиночной спирали вида

(YolV

О (Т^) /Со

(уд) _

{Ъ t

Кривая V.44 построена для значения параметров

ЛБВ, q=\ и С=0,1.

Рис. V.43. «Кривые «изменения фазов'ой

скорости вдоль участка взаимодей-

ствия. С=0,1.

Рис. V.44. Кривые изменения шага одиночной спи-

рали при kci=0,05; ctg г|?о=15; д= 1; С=0,1.

Другой способ введения изохронности базируется на

постоянстве расстройки между средней скоростью элек-

тронов и фазовой скоростью невозмущенной волны.

.237

Средняя скорость Ойределйется из coof-

йошения

2к

V 1 dff о

Va 2л \ г дФ_

1+С

дЬ

(V.31)

Параметр несинхронности в этом случае определяет-!

ся по формуле

Из этих соотношений получаем следующую формулу

для определения параметра несинхронности:

<*ъ

дФ

(V.33)

где b

=-j~r №—

^—значение параметра несинхрон-

* ности на входе в участок взаимо-

действия.

Решая систему нелинейных интегро-дифференциаль-

иых уравнений (IV.35), (IV.20) и (IV.21) совместно с со-

отношением (V.33), можно получить значение к. п. д.

ЛБВ, изохронность <в 'которой введена предложенным

способом. Результаты расчета показали, что зависи-

мости максимального к. п. д. от различных параметров

ЛБВ полностью совпадают с аналогичными зависимо-

стями, полученными при введении изохронности на осно-

ве постоянной расстройки между среднеквадратичной

скоростью электронов и «горячей» скоростью волны, т. е.

с результатами, полученными -в предыдущем случае.

Третий метод введения изохронности основан на по-

стоянстве расстройки между начальной -скоростью элек-

тронов и фазовой скоростью возмущенной -волны.

В этом случае параметр несинхронности определяет-

ся по формуле

ШЯШШ

где

Уф

— «горячая» фазовая скорость волны в системе.

238

Выше было показано, что фазовую -скорость возму-

щенной волны в системе можно определить по формуле

4;=—Ш <

Подставляя соотношение (V.35) в (V.34), получаем

* = (V.36)

Соотношение (V.36) определяет значение параметра

несинхронности при выполнении условия постоянства

расстройки между начальной скоростью электронов и

фазовой скоростью возмущенной волны.

Приведем соотношение (V.36) к более удобному ви-

ду. Для этого безразмерную величину напряженности

поля представим в виде

шшщ

тогда

a = arctg-^- (V.37)

-Подставляя (V.37) в (V.36) и производя дифферен-

цирование, находим

dF 1 dF2

db db Щ

Щ 8 (V.38)

Совместное решение системы основных интегро-диф-

ференциальных уравнений нелинейной теории ЛБВ

с соотношением (V.38) позволяет исследовать изохрон-

ную ЛБВ при требовании постоянства расстройки меж-

ду начальной скоростью электронов и возмущенной фа-

зовой скоростью волны системы. На рис. V.45—V.47

приведены некоторые результаты расчета. Пунктирными

кривыми на этих рисунках показаны соответствующие

зависимости, полученные введением изохронности пер-

вым способом. Как и в предыдущих случаях, начальное

значение параметра несинхронности было выбрано опти-

мальным для линейного режима работы ЛБВ, так как

в этом случае введение изохронности дает наибольший

эффект.

.239

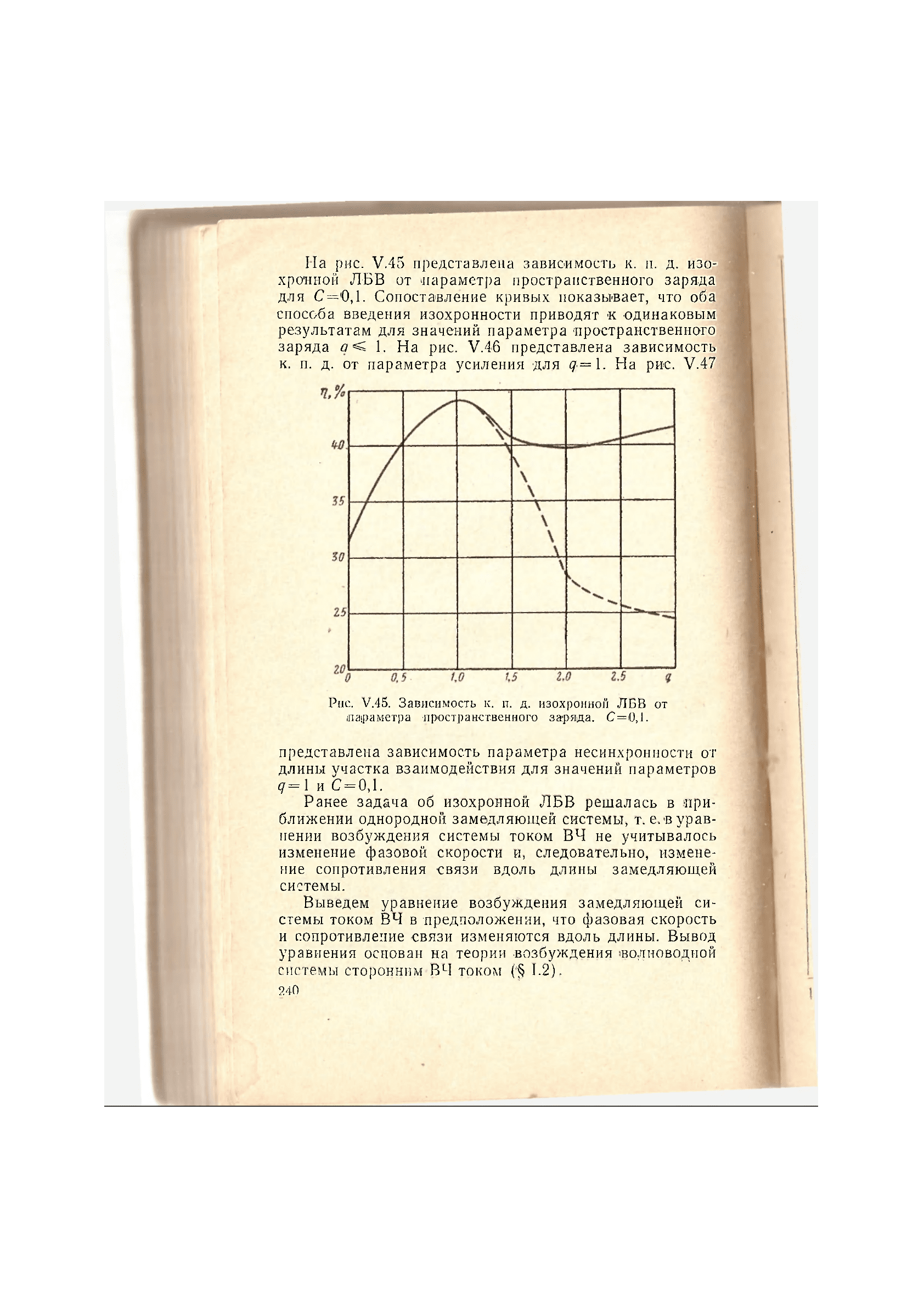
Рис. V.45. Зависимость к. п. д. изохронной ЛБВ от

параметра пространственного заряда. С=0,1.

На рис. V.45 представлена зависимость к. п. д. изо-

хронной ЛБВ от «параметра пространственного заряда

для С=0,1. Сопоставление кривых показывает, что оба

способа введения изохронности приводят к одинаковым

результатам для значений параметра пространственного

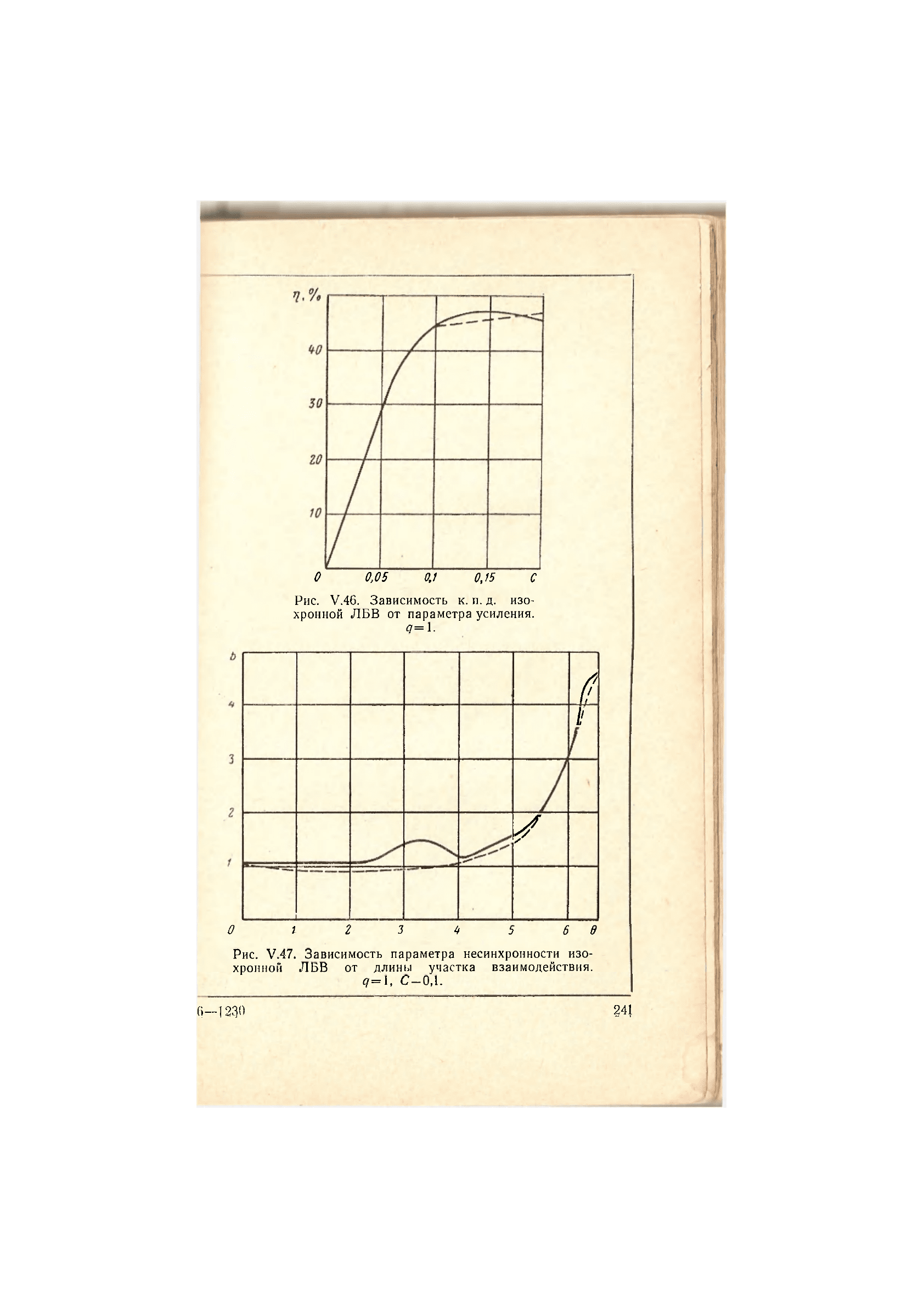
заряда 1. На рис. V.46 представлена зависимость

к. п. д. от параметра усиления для

q<=

1. На рис. V.47

представлена зависимость параметра несинхронности от

длины участка взаимодействия для значений параметров

<7=1

С=0,1.

Ранее задача об изохронной ЛБВ решалась в при-

ближении однородной замедляющей системы, т. е. в урав-

нении возбуждения системы током ВЧ не учитывалось

изменение фазовой скорости и, следовательно, измене-

ние сопротивления связи вдоль длины замедляющей

системы.

Выведем уравнение возбуждения замедляющей си-

стемы током ВЧ в предположении, что фазовая скорость

и сопротивление связи изменяются вдоль длины. Вывод

уравнения основан на теории возбуждения волноводной

системы сторощшМ'ВЧ током ('§ 1.2)

240

О 0,05

0,1

0,15 С

Рис. V.46. Зависимость к. п. д. изо-

хронной ЛБВ от параметра усиления.

Ш.

О Г 2 3 4 5 5 в

Рис. V.47. Зависимость параметра несинхронности изо-

хронной ЛБВ от длины участка взаимодействия.

<7=1, С—0,1-

Q—1230

24}

Поле, возбуждаемое ВЧ током /(£), находящимся

в окрестности d\ точки определяется соотношением

Е (?)

= - f

(?) Ко (?)

(?) (V.39)

где

Го

— постоянная распространения волны в холодном

волноводе;

/Со

— сопротивление связи.

При получении выражения (V.39) предполагалось,

что затухание в системе отсутствует и параметры систе-

мы изменяются достаточно медленно. Рассматривается

только одна «волна, фазовая скорость которой близка

к скорости электронов (активная часть поля). В холод-

ной системе поле изменяется по закону

-Г г

0 (*)<<*

= Е

. (V.40)

Поток мощности в системе, вызванный полем £о»

в точке

определяется соотношением

(Ё)

/>(£) = . (V.41)

2Г§ (g) /Со

(g)

v ;

Так как в системе без потерь поток мощности не за-

висит от координаты g, то очевидно, что в любой точ-

ке Z>1

(z)

«ti

42)

откуда

Воспользовавшись (V.39) и (V.40), получим

-Jr

\t)dt

о (*)

(?)

УК

(г) К

(?) е * , (V.44)

Соотношение (V.44) опреДелйёт поле ё тбчКе Z, Ё03-

бужденное элементом тока, находящимся в окрестности

точки Полное поле в точке z определяется

тока /(-£) d\. Пренебрегая полем, распространяющимся

в отрицательном направлении оси z (обратное излуче-

ние), находим

(V.45)

Дифференцируя (V.45) по z

получаем дифферен-

циальное уравнение для .поля, возбуждаемого в неодно-

родной волноводной системе сторонним ВЧ током i(z):

ЩШ

(z)

{z)

(z) dz

(г) d<

E =

= -±r

(z)Ko(z)i(z).

(V.46)

Переходя к безразмерным величинам и к системе ко-

ординат, движущейся со скоростью электронов, полу-

чаем следующее уравнение:

jb(Q)

(9)

о(0)

Cb (0)

db 2К

(6)

Кр(Ъ)

Ко

(0)

F =

[14-С6(0)]

МгА,. (V.47)

где /Со(0)—значение сопротивления связи на входе

в участок взаимодействия.

Совместное решение уравнения (V.47) и уравнений

(IV.20) и (IV.21) позволяет решить задачу об изохрон-

ной ЛБВ с учетом изменения фазовой скорости и сопро-

тивления связи вдоль замедляющей системы. Из урав-

нения (V.47) следует, что для решения этой задачи не-

обходимо знать как закон изменения параметра несин-

хронности, так и закон изменения сопротивления связи

вдоль системы. Поэтому в общем случае эта задача не

может быть решена. Мы воспользуемся результатами

VI гл., где приведена приближенная аналитическая за-

13* 105