Catuneanu O. Principles of Sequence Stratigraphy

Подождите немного. Документ загружается.

for any falls in base level. This highly diachronous

end-of-fall surface cannot be used as a systems tract or

sequence boundary, and it does not have a sedimento-

logical or stratigraphic signature in the rock record.

In contrast, Hunt and Tucker’s (1992) correlative

conformity, which represents the youngest clinoform

of forced regression (Fig. 6.2), is independent of the

offshore variations in subsidence rates, and its timing

is controlled solely by the balance between subsidence

and sea-level change at the shoreline. As such, along

dip-oriented transects, the offshore portion of the correl-

ative conformity may form under rising or falling base-

level conditions, depending on the subsidence patterns

within the basin. This discussion reiterates the impor-

tance of the shoreline for the transfer of terrigenous

sediment into the marine basin, and as a reference for

the overall stratigraphic architecture of the basin fill,

including the timing of all sequence stratigraphic

surfaces, independent of the offshore variations in subsi-

dence rates.

Maximum Regressive and Maximum

Flooding Surfaces

Definition

The main controversy with respect to the methods

of definition, and the impact of these definitions on the

temporal attributes of the sequence stratigraphic

surfaces in question, rests with the marine portions of the

maximum regressive and maximum flooding surfaces.

They are currently defined on the basis of (1) overall

grading and stratal stacking patterns; or (2) bathymetric

(water-depth) changes. Although these two approaches

are often considered equivalent, being used interchange-

ably (e.g., Embry, 2002, 2005), they allow for different

temporal significances for each surface (Catuneanu et al.,

1998b). As discussed earlier in this chapter, grading

trends in marine deposits and water-depth changes do

not necessarily correlate, as, for example, coarsening-

upward successions may prograde into both shallow-

ing and deepening water (Figs. 7.14 and 7.20).

The marine portion of the maximum regressive

surface is part of the transgressive–regressive (T–R)

sequence boundary, and only a systems tract bound-

ary in the view of the depositional and genetic strati-

graphic models (Fig. 4.6). It may be defined either:

(1) on the basis of stratal stacking patterns, as a

conformable surface that separates regressive strata

(progradational, coarsening-upward trend) below

from transgressive strata (retrogradational, fining-

upward trend) above; or: (2) on the basis of bathymetric

(water-depth) changes, as a conformable surface record-

ing the start of a deepening episode, i.e., formed when

the water depth reaches the shallowest peak (Embry,

2002, 2005).

Although these two definitions are considered

equivalent, they allow for different temporal signifi-

cances for the maximum regressive surface. The

former relates to the shoreline shifts and the associated

changes in stacking patterns, which bring the maxi-

mum regressive surface to a quasi-time line in a depo-

sitional dip section, independent of the offshore

variations in subsidence and sedimentation rates, as

there is only one point in time where the shoreline is at

its most basinward position. A low diachroneity rate is,

however, expected in relation to the rates of sediment

transport along dip, as in the case of the correlative

conformities discussed above. The sediment supplied to

the basin during shoreline regression generates a

coarsening-upward marine succession related to the

basinward facies shift, overlain by finer (and fining-

upward) transgressive strata. This provides a litho-

logical criterion to pinpoint the maximum regressive

surface in outcrops or subsurface logs (e.g., Figs. 4.32

and 4.37).

The second definition implies a potentially highly

diachronous maximum regressive surface, as water-

depth changes depend on varying sedimentation and

subsidence rates across the basin. In this light, it is

recognized that this type of ‘maximum regressive

surface’ is younger in areas with higher sedimentation

and lower subsidence rates, where the transition from

shallowing to deepening occurs later, although this

diachroneity is considered ‘low’ (Embry, 2002, 2005).

The diachroneity rate of this type of surface, defined

on water-depth changes, is investigated below in this

section by means of numerical modeling. Besides the

actual degree of diachroneity, which, on its own, is a

critical issue, the maximum regressive surface defined

at the top of a ‘shallowing-upward’ succession may

suffer from another significant limitation, which is the

fact that it may not develop across the entire marine

portion of the sedimentary basin. This is evident in

the actively subsiding portions of sedimentary basins

where subsidence rates outpace the sum of sea-level

change and sedimentation; in such regions, water

deepening may be continuous during several cycles of

base-level changes at the shoreline, and hence the

development of surfaces defined on the basis of bathy-

metric changes is restricted to the shallow-water portions

of the basin where subsidence rates are lower and sedi-

mentation rates are higher (Catuneanu et al., 1998b).

This aspect concerning the lateral extent of surfaces

defined on the basis of water-depth changes is also

explored in the numerical models presented below.

Similarly, the marine portion of the maximum flood-

ing surface may also be defined in two alternative

ways: (1) on the basis of stratal stacking patterns, mark-

ing the change from fining-upward, retrogradational

(transgressive) strata below to coarsening-upward,

310 7. TIME ATTRIBUTES OF STRATIGRAPHIC SURFACES

progradational (regressive) strata above (‘downlap

surface’ of Galloway, 1989); or: (2) on the basis of

bathymetric (water-depth) changes, being formed

when the water reaches the deepest peak (i.e., at the

top of a deepening-upward succession; Embry, 2002).

Again, these two methods define surfaces which are

not necessarily superimposed. In the former approach,

the maximum flooding surface corresponds to the

moment in time when the shoreline is at its landward-

most position along each depositional dip section

(Fig. 5.5). In other words, the timing of the maximum

flooding surface depends on the change in the patterns

of sediment supply associated with the shift in shore-

line trajectories, from transgressive to highstand

normal regressive, irrespective of the offshore varia-

tions in subsidence or water depth. Even so, a low

diachroneity is recorded along dip in relation to the

rates of offshore sediment transport. In addition to

this, a more significant diachroneity may exist along

the depositional strike, as variations in subsidence

and sedimentation rates may cause temporally offset

transitions from transgression to regression along

the shoreline (Gill and Cobban, 1973; Martinsen and

Helland-Hansen, 1995). Where offshore sedimentation

rates are very low around the time of maximum shore-

line transgression, determining the maximum flood-

ing surface within a condensed section may be very

difficult; in such cases, the more readily recognizable

base of the overlying terrigenous progradational

wedge (limit between the condensed section and the

overlying progradational shoreface facies in Fig. 5.5)

may be approximated as the downlap surface. This

‘maximum flooding surface’ (in reality, a facies contact

within the highstand systems tract) is, however, highly

diachronous, with the rates of highstand shoreline

regression, which can be emphasized using volcanic

ash layers as time markers (Ito and O’Hara, 1994). The

real maximum flooding surface, which corresponds to

the peak of finest sediment at the top of the retrograd-

ing succession, has a much lower diachroneity and lies

at the heart of the condensed section. Most importantly,

maximum flooding (and maximum regressive) surfaces

defined on the basis of stratal stacking patterns have a

basin-wide extent, as they reflect major changes in sedi-

ment supply and depositional trends that are triggered

by shifts in shoreline trajectories, in a manner that is

independent of the offshore variability in water depth.

The second method of definition implies a poten-

tially highly diachronous maximum flooding surface

along both dip and strike, as the timing of the peak of

deepest water depends on the variations in sedimenta-

tion and subsidence rates across the basin. As noted by

Naish and Kamp (1997), T. Naish (pers. comm., 1998),

Catuneanu et al. (1998b) and Vecsei and Duringer

(2003), the maximum water depth often occurs within

the highstand (normal regressive) progradational

wedge (Fig. 7.18). Thus, the boundary between

prograding and retrograding geometries (‘downlap

surface’) corresponds to a physical surface, recognizable

on the basis of stratal stacking patterns (e.g., Figs. 4.39

and 4.40); in contrast, the surface that marks the peak

of deepest water may be undeterminable lithologi-

cally, and may only be identified by using benthic

foraminiferal paleobathymetry. The latter ‘maximum

flooding surface,’ taken at the top of a deepening-

upward succession, is younger in areas of lower

sedimentation and higher subsidence rates, where the

transition from deepening to shallowing occurs later,

although this diachroneity is considered ‘low’ (Embry,

2002). The diachroneity rate that may characterize

this type of surface, defined on water-depth changes,

is quantified below by means of numerical modeling.

Besides the actual degree of diachroneity, what hampers

the applicability of maximum flooding surfaces defined

at the top of ‘deepening-upward’ successions most is

their spatial restriction to shallower areas within the

marine basin, where cycles of water deepening and

shallowing accompany the transgressive—regressive

shifts of the shoreline. Outside of these areas, the

actively subsiding portions of the basin may record

continuous water deepening during several base-level

cycles at the shoreline, as a result of subsidence rates

outpacing the sum of sea-level change and sedimenta-

tion (Catuneanu et al., 1998b).

End-member boundary conditions can be applied

to surfaces formed as a result of the complex interplay

between eustasy, subsidence, and sedimentation, such

as the maximum regressive and maximum flooding

surfaces defined on the basis of water-depth changes.

The temporal significance of these surfaces will be

compared with the timing of surfaces defined on the

basis of stratal stacking patterns.

Two-dimensional Model

To illustrate the effect that subsidence and sedimen-

tation rates have on the timing of maximum regressive

and maximum flooding surfaces defined on the basis

of bathymetric changes, a simple two-dimensional

geometrical basin model applied to a marine shelf

setting is constructed, which is referred to in the follow-

ing as Profile A. The model considers eustasy as the

highest-frequency variable, to facilitate comparison with

the depositional sequence model of Posamentier et al.

(1988), but similar results may be obtained by taking

subsidence as the higher-frequency parameter instead.

The input values used for the variable rates of change

are obtained from the literature (Pitman, 1978; Pitman

and Golovchenko, 1983; Angevine, 1989; Galloway, 1989;

Jordan and Flemings, 1991; Macdonald, 1991; Frostick

and Steel, 1993).

METHODS OF DEFINITION OF STRATIGRAPHIC SURFACES 311

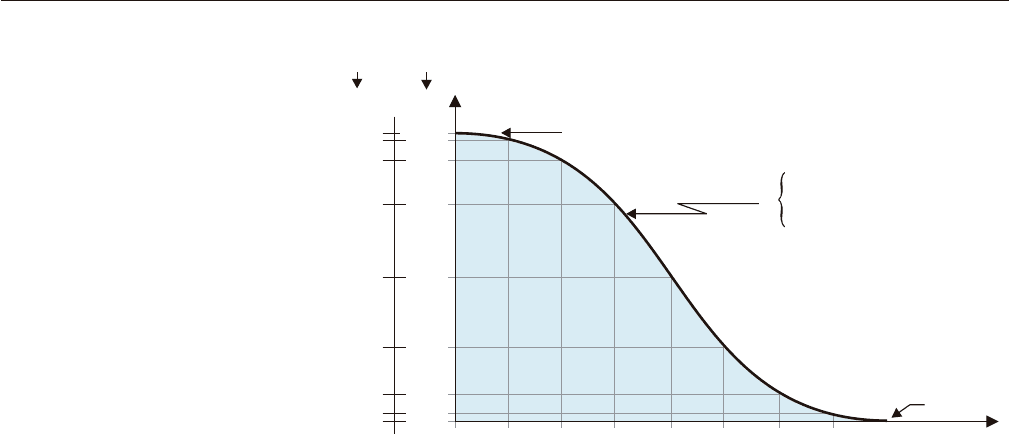
The assumptions of the model are as follows:

1. Eustasy varies sinusoidally with an amplitude of

10 m and a period of 2 Ma (Fig. 7.23). For the sake

of brevity, only half of the eustatic cycle is shown,

from highstand to lowstand. The rate of eustatic fall

increases from zero at highstand (0 Ma) to a maxi-

mum of 15.7 m/Ma at the inflexion point (0.5 Ma),

and then decreases to zero at lowstand (1 Ma).

2. The modeled portion of the basin is 200 km across,

and the tectonic subsidence rate is constant at

any particular point, but increases basinward from

20 m/Ma at the proximal end of the profile to

40 m/Ma at the distal end. This is similar to the

simple divergent margin models of Pitman (1978),

Angevine (1989) and Jordan and Flemings (1991).

3. The sedimentation rates change along dip in a linear

manner, decreasing from 15 m/Ma at the proximal

end of the basin profile to 5 m/Ma at the distal end.

This reflects the tendency of coarser-grained sedi-

ments to be trapped closer to the shoreline. Since

the sedimentation rate at any point along the basin

profile is a function of its distance from the shoreline,

it must therefore vary through time as the shoreline

transgresses and regresses. Incorporation of this facies

shift into the model would necessitate recalculating

the sedimentation rate at each point along the profile

at each model time step. However, at the scale of the

modeled basin profile (200 km) this is insignificant

(less than 150 m for one time step; Catuneanu et al.,

1998b), so the sedimentation rate is approximated

to be constant at any given point through time, for

simplicity.

The interplay of tectonic subsidence and sedimenta-

tion along the basin profile gives the rate and direction

of motion of the seafloor relative to the center of Earth.

Since the lateral facies shifts are negligible at the scale of

the model, the rate of vertical seafloor motion remains

constant at any particular point of the profile through

the course of the eustatic half-cycle. This rate does vary

spatially, however, reflecting the differen-tial subsidence

and sedimentation rates along the dip-oriented basin

profile.

The model advances in increments of 0.125 Ma. For

each incremental time step, the addition of the rate of

sea-level change (Fig. 7.23) to the rates of subsidence and

sedimentation at each point along the profile, allows

calculation of the rates of water-depth changes across

the basin. The result is a graphic output (Fig. 7.24) that

shows which portions of Profile A undergo water shal-

lowing and which ones undergo water deepening. The

boundary between these two zones marks the point at

which water depth is stationary, and this point shifts

with time along dip in response to the changing balance

between accommodation and sedimentation.

Model Results

The model starts at eustatic highstand, where the

rate of eustatic change is zero. The rate of water-depth

change at this time is thus equal to the rate of vertical

motion of the seafloor, and is positive along the entire

length of the profile (Fig. 7.24). The water is therefore

deepening throughout Profile A.

The successive incremental time steps of the model

through a 1 Ma eustatic half-cycle from highstand to

312 7. TIME ATTRIBUTES OF STRATIGRAPHIC SURFACES

(m)

10.00

9.62

8.53

6.91

5.00

3.08

1.46

0.38

0.125

0.25

0.375 0.50

0.625 0.75

0.875 1.00

Time (t, My

)

lowstand

22.5

45.0

67.5 90.0 112.5

135.0

157.5

180.0

Phase (α, °

)

(m/My)

highstand

F(α)=5(1+cosα), or:

0.00

6.01

11.10

14.51

15.70

14.51

11.10

6.01

0.00

f(t)=5[1+cos(πt)]

Rate of eustatic fall (m/My):

df(t)/dt=−5π

sin(πt)

Rate Sea level, relative to lowstand elevation

FIGURE 7.23 Curve of eustatic changes

considered in the numerical model (modified

from Catuneanu et al., 1998b). Eustasy is

assumed to vary sinusoidally with an

amplitude of 10 m and period of 2 Ma.

Only half the eustatic cycle (180° phase,

or 1 Ma) from highstand to lowstand is

shown. The rate of eustatic change at each

0.125 Ma time step, given by the first deriva-

tive of the sine curve, is shown on the left.

D=T-S

peak of deepest water

peak of shallowest water

tectonic subsidence

sedimentation

rate of water shallowing (−, m/My)

rate of water deepening (+, m/My)

200

28.99

23.9

20.49

19.3

6.73 km

−1.01

1. 0 My (eustatic highstand)

9. 1 My (eustatic lowstand)

2. 0.125 My

8. 0.875 My

−6.1

40.66 km

3. 0.25 My

7. 0.75 My

4. 0.375 My

6. 0.625 My

5. 0.5 My

−9.51

−10.7

63.4 km

71.33 km

Profile A

T, D

0, inner shelf

200 km

offshore

T=20-40 m/My

S=15-5 m/My

D=5-35 m/My

W=E+D

Water-depth changes (W=E+D):

maximum seaward

extent of surfaces defined

on water-depth changes

LST

TST

HST: time steps 1-5

LST: time steps 5-9

TST

Base-level curve at the shoreline

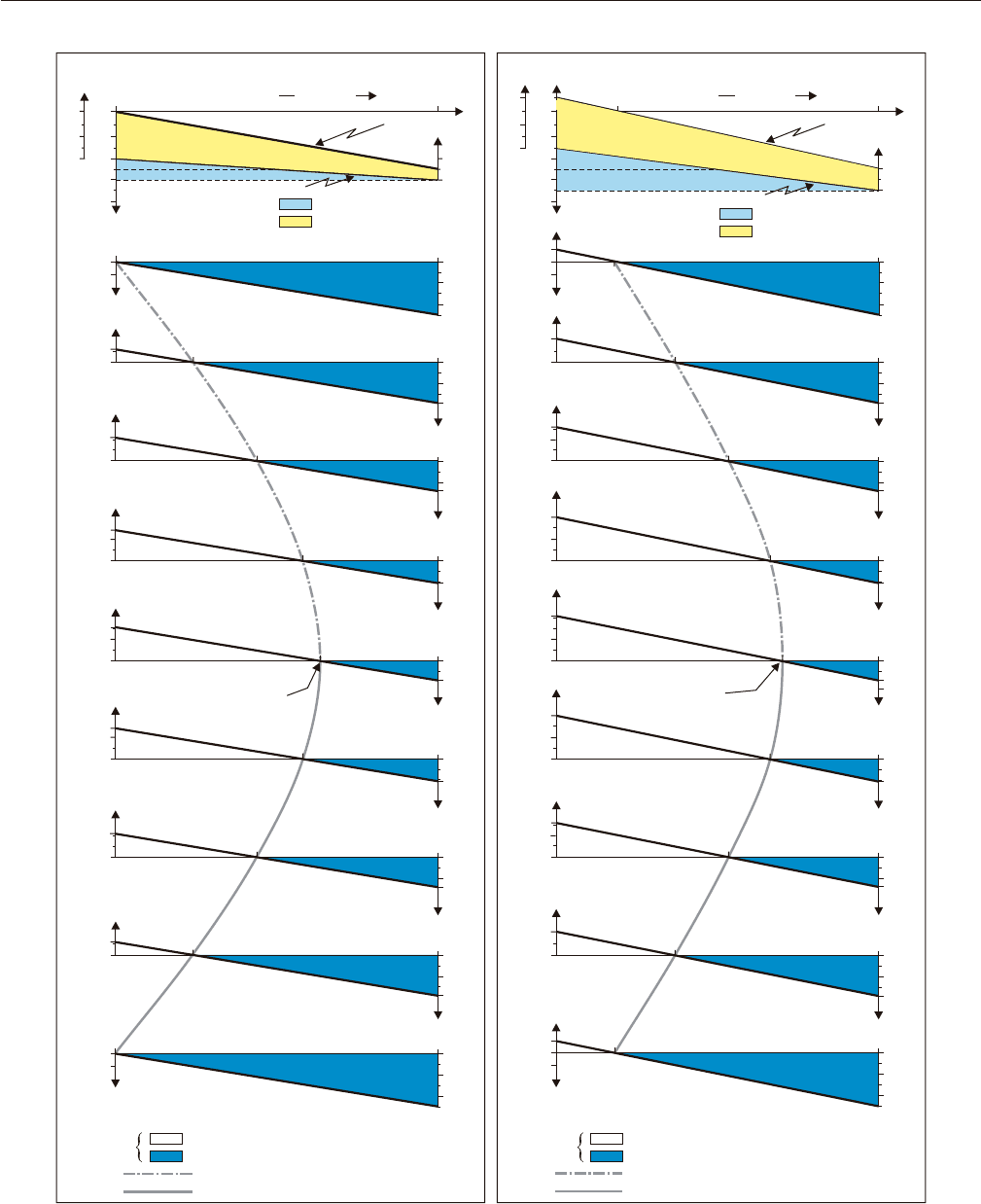
FIGURE 7.24 Timing and locus of formation of surfaces that mark the peaks of shallowest and deepest water,

along basin Profile A, as a function of the interplay between eustasy (E), subsidence (T) and sedimentation (S)

(modified from Catuneanu et al., 1998b). The input values for subsidence and sedimentation are provided on the

top cross section. The interplay of subsidence and sedimentation defines the rates of vertical shifts of the seafloor

relative to the center of Earth (D). The rate of water-depth change (W) is shown across the basin profile for nine

incremental time steps through a eustatic half cycle from highstand to lowstand. Maximum flooding and

maximum regressive surfaces defined on bathymetric changes form where the rate of water-depth change equals

zero at each time step. In this example, highstand normal regression (decelerating base-level rise) is succeeded by

lowstand normal regression (accelerating base-level rise) without an intervening stage of forced regression.

Abbreviations: LST––lowstand systems tract; TST––transgressive systems tract; HST––highstand systems tract.

lowstand are shown in Fig. 7.24. At each time step, the

distance along the profile at which the rate of water-

depth change equals zero is indicated. This is the point

at which surfaces associated with the peaks of shallow-

est or deepest water form, separating areas of coeval

water deepening and shallowing. The surface gener-

ated between time steps 1 and 5 is the maximum

flooding surface defined on bathymetric changes, as it

separates trends of water deepening below from water

shallowing above. The surface generated starting with

time step 5 is the maximum regressive surface defined

on bathymetric changes, as it corresponds to the peak

of shallowest water. As the rate of eustatic fall

increases from time step 1 to 5 (Fig. 7.23), a progressively

larger value of net subsidence is required to balance it

and maintain the stationary water-depth condition

that ends the deepening-upward trend. This point of

balance shifts basinward through time, and therefore

the maximum flooding surface defined on bathymetric

changes is younger offshore than it is towards the

basin margin.

Time step 5 (0.5 Ma) is the inflexion point on the

falling limb of the sinusoidal eustatic curve and represents

the maximum rate of eustatic fall. This is balanced by

subsidence and sedimentation at a distance of 71.3 km

along the profile (Fig. 7.24). Basinward of this point,

shallowing is not possible anymore, so the water is

continuously deepening. Under these circumstances,

no more surfaces defined on water-depth changes can

form beyond this point.

During time steps 5 to 9 the rate of eustatic fall

decreases to zero. As the rate of eustatic fall decreases,

it is balanced by a progressively lower value of verti-

cal seafloor shift, and the point of balance between

shallowing- and deepening-water conditions moves

towards the basin margin. The surface that marks the

peak of shallowest water is therefore older offshore

than it is towards the basin margin (Fig. 7.24). At time

step 9 (eustatic lowstand), continued subsidence results

in a water deepening trend across the entire profile.

Strike Variability

To further illustrate the diachroneity of surfaces

defined on water-depth changes, two more basin profiles

(B and C) are added to the model. These represent dip-

sections across the same basin at 50 and 100 km along

strike from Profile A. Profiles B and C are assigned

slightly different values of subsidence and sedimentation

rates, to reflect the type of strike variability that is

commonly found in the real world. All three models

are run through the same eustatic half-cycle.

The graphic incremental time steps for Profiles B

and C are shown in Fig. 7.25. The time/distance data for

the formation of the two surfaces defined on water-depth

changes along profiles A, B, and C can be used to

construct isochrone maps of these surfaces, as illustrated

in Fig. 7.26. The isochrones join the points where the

formation of the two surfaces was synchronous on the

three profiles. As seen on the cross sections and maps

(Figs. 7.24–7.26), the diachroneity of the modeled

surfaces approaches 0.5 Ma along dip, within a distance

of less than 200 km, which is compatible with the

resolution of ammonite zonation for the Jurassic and

the Cretaceous (Obradovich, 1993).

It should also be noted that the shallowing-upward

trend does not extend across the entire basin but is

replaced by continuous deepening beyond the point

where the sum of subsidence and sedimentation starts

to outpace the rates of eustatic fall on a permanent

basis (Figs. 7.24 and 7.25). This is an important obser-

vation because it emphasizes the fact that maximum

flooding and maximum regressive surfaces defined on

water-depth changes may join offshore before reaching

the basin center, which defeats the primary purpose

of sequence stratigraphy which is to map bounding

surfaces with basin-wide extent.

Discussion

The model run presented in Figs. 7.23–7.26 demon-

strates that maximum flooding and maximum regres-

sive surfaces defined on water-depth changes are not

suitable for sequence stratigraphic analysis, for two main

reasons: (1) they potentially have a limited lateral

extent, restricted to the portion of the basin that may

be subject to shallowing trends; and (2) they may be

highly diachronous, within the range of biostrati-

graphic resolution. The timing of these surfaces (desig-

nated as ‘type B’ maximum flooding and maximum

regressive surfaces by Catuneanu et al., 1998b) depends

on the offshore variations in subsidence and sedimen-

tation rates, which explains the high diachroneity rates.

In contrast, the formation of maximum flooding and

maximum regressive surfaces defined on stratal stacking

patterns (designated as ‘type A’ by Catuneanu et al.,

1998b) is independent of the offshore variations in subsi-

dence and sedimentation rates, similar to the correlative

conformities of Posamentier and Allen (1999) and Hunt

and Tucker (1992).

The diachronous character of the type B maximum

flooding and maximum regressive surfaces has been

recognized by Embry (2002), even though only on a

non-quantified basis. The peak of shallowest water is

correctly envisaged to be younger in areas of higher

sedimentation rates, i.e., adjacent to the shoreline, but

the degree of diachroneity is thought to be limited to

the duration of the lowstand normal regression: ‘the

change from a shallowing-upward trend to a deepening-

upward one [i.e., the ‘maximum regressive surface’ of

314 7. TIME ATTRIBUTES OF STRATIGRAPHIC SURFACES

METHODS OF DEFINITION OF STRATIGRAPHIC SURFACES 315

D=T-S

tectonic subsidence

sedimentation

rate of water shallowing (−, m/My)

rate of water deepening (+, m/My)

200

18.99

13.9

10.49

9.3

48.08 km

−6.01

1. 0 My (eustatic highstand)

9. 1 My (eustatic lowstand)

2. 0.125 My

8. 0.875 My

−11.10

88.8 km

3. 0.25 My

7. 0.75 My

4. 0.375 My

6. 0.625 My

5. 0.5 My

−14.51

−15.7

116.08 km

125.6 km

Profile B

T, D

0, inner shelf

200 km

offshore offshore

T=20-30 m/My

S=20-5 m/My

D=0-25 m/My

Water-depth changes (W=E+D):

W=E+D W=E+D

D=T-S

peak of deepest water

peak of shallowest water

peak of deepest water

peak of shallowest water

tectonic subsidence

sedimentation

rate of water shallowing (−, m/My)

rate of water deepening (+, m/My)

200

−5

18.99

13.9

10.49

9.3

73.4 km

−11.01

1. 0 My (eustatic highstand)

9. 1 My (eustatic lowstand)

2. 0.125 My

8. 0.875 My

−16.1

107.33 km

3. 0.25 My

7. 0.75 My

4. 0.375 My

6. 0.625 My

5. 0.5 My

−19.51

−20.7

130.06 km

138 km

Profile C

T, D

inner shelf

200 km

T=15-35 m/My

S=20-10 m/My

D=−5-25 m/My

−5

33.33 km

maximum seaward

extent of surfaces defined

on water depth changes

maximum seaward

extent of surfaces defined

on water depth changes

FIGURE 7.25 Incremental output of Profiles B and C model runs (modified from Catuneanu et al., 1998b).

These profiles are assigned different rates of subsidence and sedimentation relative to Profile A, but the same

eustatic curve shown in Fig. 7.23 was used. See Fig. 7.24 for the key to abbreviations.

Embry, 2002] … begins to form in basinward localities

at the start of base level rise and ends at the start of

landward movement of the shoreline’ (Embry, 2002).

This assessment is only valid if the water was shallow-

ing across the entire basin during the forced regression

of the shoreline, which is generally the case where

base-level changes are solely controlled by eustasy.

Differential subsidence, however, may result in base-

level rise and water deepening offshore, coeval with a

fall in base level at the shoreline (e.g., Vail et al, 1984;

Catuneanu et al., 1998b). This means that the type B

maximum regressive surface, which corresponds to

the peak of shallowest water, may actually start form-

ing during forced regression, and therefore before the

start of base-level rise at the shoreline; in such cases,

the earliest portion of the type B maximum regressive

surface becomes coeval with the subaerial unconfor-

mity, and is older than the correlative conformity of

Hunt and Tucker (1992). This surface continues to form,

younging landwards, until the shoreline starts its

transgressive shift. The spatial and temporal relation-

ships that can be demonstrated between the subaerial

unconformity, its correlative conformity, and the type B

maximum regressive surface indicates the inadequacy

of using bathymetric criteria for the definition of any

sequence stratigraphic surface.

The type B maximum flooding surface (peak of deep-

est water) begins to form when the shoreline reaches

maximum transgression, starting in nearshore areas,

where sedimentation rates are highest and the change

from deepening- to shallowing-upward trends occurs

earlier, expanding gradually basinward throughout

the highstand normal regression. In basins where the

forced regression of the shoreline is coeval with base-

level rise and water deepening offshore (e.g., Vail et al.,

1984; Catuneanu et al., 1998b), the formation of the

type B maximum flooding surface continues after the

end of highstand normal regression, during the subse-

quent base-level fall at the shoreline. In such cases, the

youngest portion of the type B maximum flooding

surface may be coeval with the subaerial unconfor-

mity, and is therefore younger than the basal surface of

forced regression (correlative conformity of Posamentier

and Allen, 1999). This, again, points out the inadequacy

of using bathymetric criteria for the definition of

sequence stratigraphic surfaces.

Even in cases where the type B maximum regressive

and maximum flooding surfaces have their interval

of formation restricted to stages of lowstand and high-

stand normal regressions, respectively, as postulated

by Embry (2002), the degree of diachroneity can still

be ‘high,’ depending on the duration of these stages.

Figure 7.24 provides such an example, where lowstand

and highstand stages last sufficiently long to allow for

the formation of highly diachronous type B surfaces,

within the biostratigraphic resolution. Perhaps even

more significant to point out, however, is that the gener-

alization that type B maximum regressive and maxi-

mum flooding surfaces form during stages of lowstand

and highstand normal regressions, respectively, is only

valid for sedimentary basins characterized by subsi-

dence rates that increase basinward, as modeled by

Catuneanu et al. (1998b). In contrast, as discussed

earlier in this chapter, sedimentary basins whose subsi-

dence rates decrease basinward (e.g., flexural forelands)

may support the formation of type B maximum regres-

sive and maximum flooding surfaces during transgres-

sions instead.

These points can be demonstrated easily using

numerical models. The data input for the forward

simulations in Figs. 7.24 and 7.25 account for a situa-

tion where subsidence rates are generally greater than

the rates of eustatic fall. This is a case of continuous

316 7. TIME ATTRIBUTES OF STRATIGRAPHIC SURFACES

Profile C

Profile B

Profile A

Distance along dip (km)

Distance along strike (km)

seaward extent of

shallowing trend

seaward extent of

shallowing trend

0.875

0.125

0.75

0.25

0.625

0.375

0.5

0 50 100 150 200

0 50 1000 50 100

1. Timing of the surface that marks the peak of

deepest water (i.e., maximum flooding surface

defined on the basis of water-depth changes)

2. Timing of the surface that marks the peak of

shallowest water (i.e., maximum regressive surface

defined on the basis of water-depth changes)

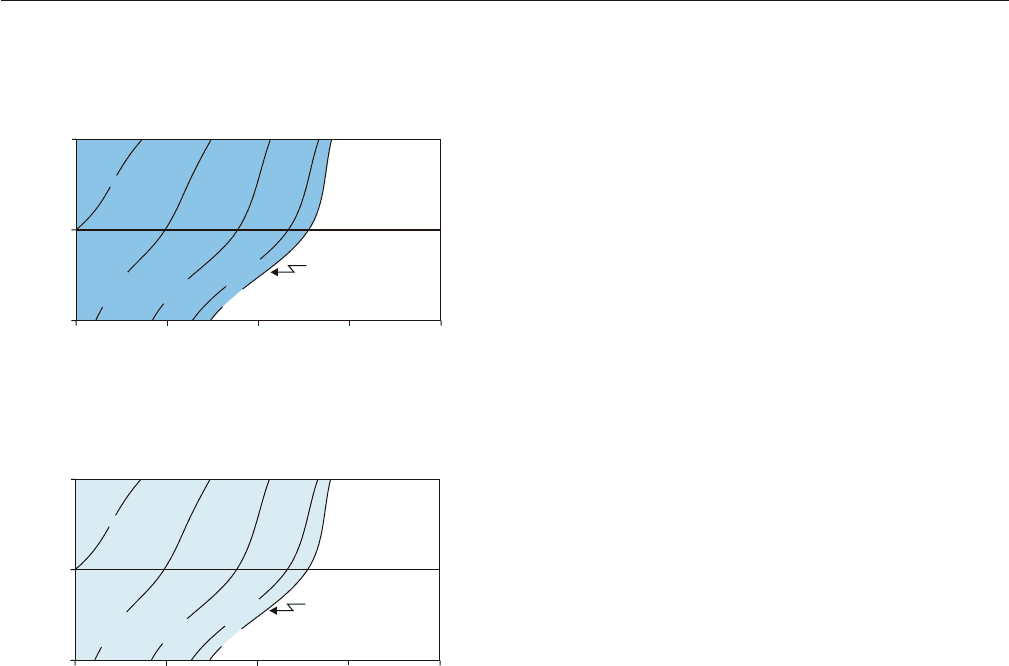
FIGURE 7.26 Isochrone maps of the two surfaces defined on the

basis of water-depth changes (modified from Catuneanu et al.,

1998b). Note that these surfaces have a limited extent in an offshore

direction, and join along the line that marks the maximum extent of

shallowing trends. The isolines on the map show the locus of surface

formation for each time step of the model run.

relative sea-level rise, where the transgressive and

(normal) regressive shifts of the shoreline are mainly

controlled by sedimentation and varying rates of sea-

level change. Under such circumstances, highstand

normal regressions (decelerating base-level rise) are

immediately succeeded by lowstand normal regres-

sions (accelerating base-level rise) without intervening

stages of forced regression (e.g., Fig. 7.24). Profile D

(Fig. 7.27) depicts the same basin profile considered in

Figs. 7.24 and 7.25, but this time affected by lower

subsidence rates that are within the range of eustatic

fluctuations. The results of the model run show that

the relative sea level falls and rises through time at the

shoreline, whereas offshore, beyond the point of maxi-

mum extent of relative sea-level fall (i.e., where subsi-

dence starts outpacing the highest rate of eustatic fall),

the basin is subject to continuous relative sea-level rise.

This is the situation envisaged by Vail et al. (1984) for

the formation of type 2 sequence boundaries: eustatic

fall outpacing subsidence at the shoreline (forced

regression) coeval with relative rise at the shelf edge

(subsidence outpacing eustatic fall). The interplay of

relative sea-level changes and sedimentation determines

the timing of formation of surfaces marking the peaks

of shallowest and deepest water (Fig. 7.27). Note that

these surfaces (1) have limited lateral extent in a basin-

ward direction; (2) meet at the point where water is

beyond the influence of shallowing conditions (subsi-

dence > eustatic fall + sedimentation); and (3) form not

only during normal regressions of the shoreline, but

also during forced regression, in parallel with the

formation of the subaerial unconformity. The calcu-

lated diachroneity rate of these surfaces approaches a

quarter of the period of the highest-frequency variable

(eustasy in this case, with a period of 2 Ma; Catuneanu

et al., 1998b), which is in agreement with the quarter-cycle

phase shift modeled by Angevine (1989), Christie-Blick

(1991) and Jordan and Flemings (1991).

Figure 7.28 presents a Wheeler diagram that shows

the timing of types A and B maximum flooding and

maximum regressive surfaces, and also the changing

balance between relative sea-level rise and fall along

dip. Note that the influence of relative fall diminishes

in a basinward direction in parallel to the increase in

subsidence rates. Similarly, shallowing-water condi-

tions are also less prevalent in a basinward direction,

and they eventually stop manifesting altogether where

subsidence exceeds the sum of sedimentation and

maximum sea-level fall.

It is now clear that any type of surface whose timing

depends on the offshore variations in subsidence and

sedimentation rates is bound to have a potentially high

diachroneity and limited lateral extent. Both these two

attributes make such surfaces inadequate for sequence

stratigraphy and regional correlations; what is needed,

instead, are surfaces with basin wide extent and low

diachroneity rates. These ‘ideal’ surfaces are repre-

sented by the type A maximum flooding and maxi-

mum regressive surfaces, the basal surface of forced

regression (the correlative conformity of Posamentier

and Allen, 1999), and the correlative conformity sensu

Hunt and Tucker (1992). These four surfaces correspond

to the four events of the base-level cycle at the shore-

line (Figs. 1.7 and 4.7), and are independent of the

offshore variations in subsidence and sedimentation

rates (Fig. 7.28). They are defined based on stratal stack-

ing patterns (separating forced regressive vs. normal

regressive vs. transgressive stratal architectures), with a

timing controlled by the changes in the direction

and/or type of shoreline shift. Such changes in shore-

line trajectories control the patterns of sediment

supply to the marine basin, and hence the stratal

geometries and depositional trends referred to above.

The curves that indicate changes in water depth

and relative sea level along dip follow each other

closely (Fig. 7.28), displaying parallel trends offset

with the value of the sedimentation rates. These time-

transgressive curves meet the shoreline at the four key

points of the base-level cycle (Figs. 1.7 and 4.7), where

they join the four quasi-isochronous sequence strati-

graphic surfaces defined on stratal stacking patterns

(type A in Fig. 7.28). As the correlative conformity

(sensu Hunt and Tucker, 1992) marks the end of base-

level fall at the shoreline but forms during base-level

rise offshore, the (type A) maximum regressive surface

too marks the end of shallowing near the shoreline but

forms during water deepening (in extensional basins;

potentially shallowing in forelands) offshore. Both these

surfaces top successions that prograde into the basin

during particular stages of shoreline shifts (forced and

lowstand normal regressions, respectively), irrespective

of how subsidence and sedimentation rates may vary

offshore. Following the same idea, the basal surface of

forced regression is taken at the base of all deposits

accumulated during the forced regression of the shore-

line, even though some of the deeper-water ‘forced

regressive’ sediments accumulate under rising relative

sea-level conditions (Fig. 7.28). This approach is

warranted because all these deposits are laterally

correlative and age-equivalent, with the sediment being

supplied to the basin in relation to the forced regression

of the shoreline.

The use of type B surfaces (Fig. 7.28) would

make different systems tracts to be age-equivalent, as

explained in detail by Catuneanu et al. (1998b) (their

Figs. 13 and 14). Since the type B maximum flooding

and maximum regressive surfaces may join in an area

that is shallower than the basin center, everything that

METHODS OF DEFINITION OF STRATIGRAPHIC SURFACES 317

318 7. TIME ATTRIBUTES OF STRATIGRAPHIC SURFACES

start of relative fall surface

start of relative rise surface

peak of deepest water

peak of shallowest water

tectonic subsidence (T)

subsidence & sedimentation (D)

rate of relative sea-level fall (−, m/My)

rate of relative sea-level rise (+, m/My)

rate of water shallowing (−, m/My)

rate of water deepening (+, m/My)

200

3.99

13.9

12.9

8.9

5.49

4.3

7.9

4.49

3.3

7.77 km

−1.01

1. 0 My (eustatic highstand)

9. 1 My (eustatic lowstand)

2. 0.125 My

8. 0.875 My

−1.1

−6.1

0 0

12.35 km

77.21 km

152.78 km

169.15 km

3. 0.25 My

4. 0.375 My

6. 0.625 My

5. 0.5 My 5. 0.5 My

−4.51

−9.51

−5.7

−10.7

82.14 km

132.55 km

Profile D: eustasy & tectonics Profile D: eustasy, tectonics & sedimentation

7. 0.75 My

T DD

0, inner shelf 0, inner shelf

200 km 200 km

offshoreoffshore

0 0

10 10

20 20

T=10-20 m/My

D=5-19 m/My

T=10-20 m/My

S=5-1 m/My

R=E+T W=E+D

Relative sea-level changes (R=E+T): Water-depth changes (W=E+D):

maximum seaward extent

of relative sea-level fall

maximum seaward extent

of shallowing trends

FIGURE 7.27 Diachronous formation of surfaces separating deposits accumulated under relative sea-level

fall and rise conditions (left column), as well as deposits accumulated under water deepening and shallowing

conditions (right column). See Fig. 7.24 for the key to abbreviations.

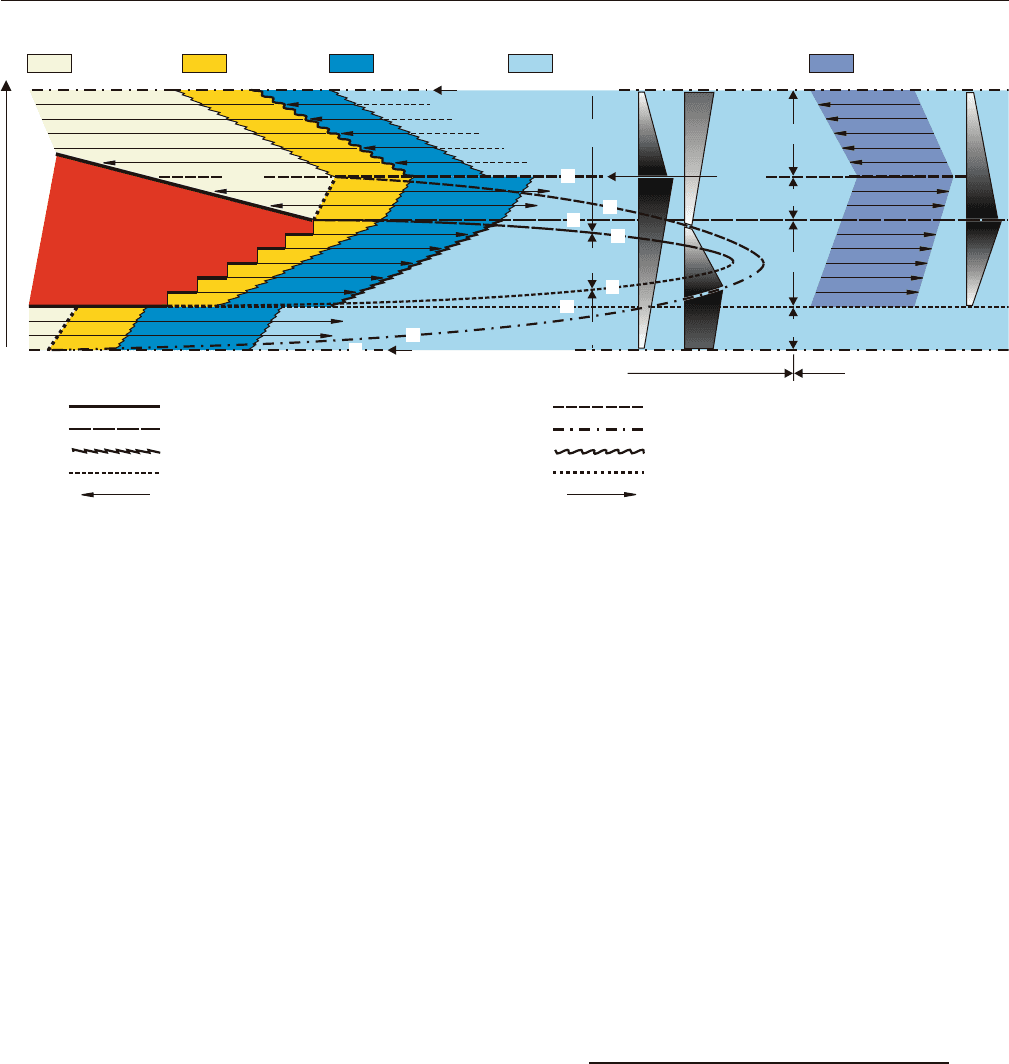
accumulates in the basin center under continuous

deepening-water conditions would qualify as a trans-

gressive systems tract, and be age-equivalent with all

other systems tracts in the shallow part of the basin.

Such a view would of course be misleading since the

bounding surfaces that separate different stacking

patterns (and associated systems tracts) are in fact

quasi-time lines (with a low diachroneity that reflects

the rates of sediment transport) along dip, independent

of the offshore variations in subsidence and sedimen-

tation rates.

An inherent and potentially higher diachroneity

along strike is recorded by all types of event-significant

surfaces in relation to the strike variability in subsi-

dence and sedimentation rates along the shoreline. The

strike diachroneity of the two correlative conformities

(base and top of forced regressive deposits) is affected

only by changes in subsidence rates, whereas the

strike diachroneity of maximum regressive and maxi-

mum flooding surfaces is also influenced, in addition

to subsidence, by fluctuations in sedimentation rates

along the shoreline. As sediment supply to the shore-

line may vary significantly along strike, the transitions

from regression to transgression and vice versa may be

offset significantly from one area to another, sometimes

within the range of biostratigraphic resolution (e.g., Gill

and Cobban, 1973). For this reason, maximum regressive

and maximum flooding surfaces tend to be less signifi-

cant than the correlative conformities in a chronostrati-

graphic framework.

SUMMARY: TIME ATTRIBUTES

OF STRATIGRAPHIC SURFACES

Subaerial Unconformity

The subaerial unconformity (Figs. 4.9 and 4.13) is

generally perceived as a ‘time barrier’ (Winter and

Brink, 1991; Embry, 2001b) based on the assumption

that time lines do not cross this surface, i.e., all strata

below the unconformity are older than the strata

above it. Whether this is a general truth or an artifact

of the lack of rigorous testing remains to be seen. The

possibility of formation of diachronous unconformities

which are crossed by time lines is emphasized in the

SUMMARY: TIME ATTRIBUTES OF STRATIGRAPHIC SURFACES 319

marine

onlap

downlap surface (MFS)

MRS

(hiatus)

f.u.

Time

c.u.

d.u.

s.u.

relative

fall

relative

rise

relative

rise

MRS

fluvial beach shoreface shelf/condensed sections

submarine fans

subaerial unconformity (SU)

correlative conformity

regressive surface of marine erosion

basal surface of forced regression

onlap

maximum regressive surface (MRS)

maximum flooding surface (MFS)

transgressive wave ravinement surface

within-trend normal regressive surface

downlap

TST

LST

HST

FSST

f.u.

c.u.

coastal

pelagics

onlap

fluvial onlap

CONTINENTAL SHELF DEEP WATER

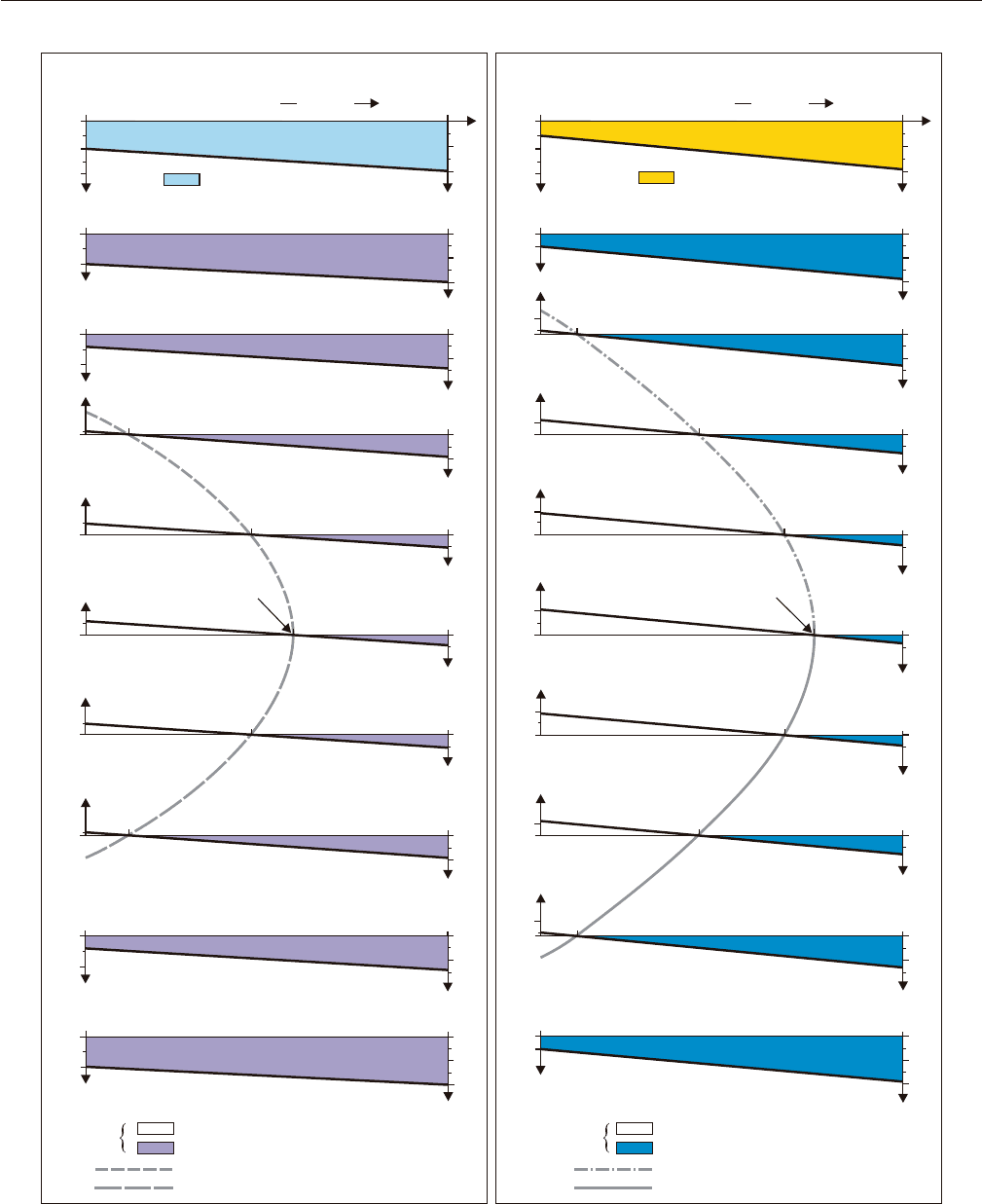
FIGURE 7.28 Temporal significance of types A and B surfaces (modified from Catuneanu et al., 1998b).

Type A surfaces are defined by stratal stacking patterns, and are systems tract boundaries. The timing of type A

surfaces depends on base-level changes, or on the interplay between base-level changes and sedimentation,

at the shoreline. The timing of type A surfaces is independent of the offshore variations in subsidence and

sedimentation rates. The timing of type B surfaces depends on the offshore variations in subsidence and

sedimentation rates, which confers on those surfaces high diachroneity rates (a quarter of the period of the

highest-frequency variable: Catuneanu et al., 1998b). Type A and B surfaces join at the shoreline, but diverge

in an offshore direction. Abbreviations: HST––highstand systems tract; FSST––falling-stage systems tract;

LST––lowstand systems tract; TST––transgressive systems tract; RST––regressive systems tract; c.u.––coarsening-

upward; f.u.––fining-upward; d.u.––deepening-upward; s.u.––shallowing-upward. Note that grading and

water-depth changes are not interchangeable concepts.