Catuneanu O. Principles of Sequence Stratigraphy

Подождите немного. Документ загружается.

This Page Intentionally Left Blank

CHAPTER

Time Attributes of Stratigraphic Surfaces

INTRODUCTION

A central and yet controversial topic in sequence

stratigraphy is the assessment of stratigraphic surfaces

in a chronostratigraphic framework. Are the bounding

surfaces of sequences and systems tracts time lines,

i.e., generated at the same time everywhere within the

basin? The answer to this question is of paramount

importance for stratigraphic correlation, and although

this problem has been debated for some time (Miall,

1991, 1994; Catuneanu et al., 1998b; Posamentier and

Allen, 1999), agreement is yet to be reached. Part of the

problem derives from the way concepts are defined,

often with contradictory meanings, as explained in

this chapter.

The assumptions made in the early days of seismic

and sequence stratigraphy, in the 1970s and 1980s,

emphasized heavily the role of eustatic changes in sea

level in the generation of the preserved stratigraphic

record, and implicitly on the formation of systems

tract and sequence boundaries. As eustatic changes in

sea level are global in nature, it was implied that

sequence stratigraphic surfaces that correspond to the

four events of the base-level cycle (Fig. 4.7) are isochro-

nous, being formed everywhere at the same time.

Subaerial unconformities, assumed to have been

formed during global stages of sea-level fall, were also

assigned global synchronicity. These early ideas led to

the construction of the global cycle chart (Vail et al.,

1977; Haq et al., 1987, 1988), whose fundamental prem-

ise was that sequence stratigraphic conformities are

world-wide correlatable time lines, while sequence-

bounding unconformities correspond to stratigraphic

hiatuses of global significance. Thus, each set of sequence

stratigraphic surfaces found in any basin around the

world was invariably traced back and correlated to the

‘global master curve,’ assuming that each stratigraphic

cycle is globally synchronous. As a result, sequence

cycles were seen as geochronologic units that provide

the means to subdivide the sedimentary rock record

into genetic chronostratigraphic intervals (Vail et al.,

1977, 1991).

The eustasy-driven stratigraphic approach provided

an easy, but oversimplified way of looking at the tempo-

ral significance of stratigraphic surfaces. In reality, no

surface can possibly be an absolute time line, and the

degree of diachroneity may vary greatly with the

mode of formation and the dependence on parameters

characterized by variable rates along dip and strike,

such as tectonism and sedimentation. While a continuum

is expected within the diachroneity range, the qualifiers

used to describe the degree of diachroneity in this book

are ‘low’ vs. ‘high’ (Fig. 4.9): a ‘low diachroneity’ refers

to a difference in age that falls below the resolution of

the current dating techniques, which therefore is unde-

tectable by biostratigraphic, magnetostratigraphic, or

radiometric means; a ‘high diachroneity’ refers to a more

significant difference in age between the different

portions of a stratigraphic surface, which can be empha-

sized using the available dating techniques.

This chapter analyzes the degrees of diachroneity

that various stratigraphic surfaces may be associated

with, by using simple numerical models. The temporal

significance of stratigraphic surfaces is arguably one

of the most difficult topics to deal with, and to quan-

tify, in sequence stratigraphy. Firstly, addressing

this topic requires computational simulations, which,

although increasingly employed in stratigraphic

analyses (e.g., Jordan and Flemings, 1991; Johnson and

Beaumont, 1995; Catuneanu et al., 1998b; Harbaugh et al.,

1999), are still not fully embraced by the majority of

geologists as part of their workflow routine. Secondly,

the methods of defining stratigraphic surfaces are

to some extent loose, from the generic nature of the

reference curve relative to which sequence stratigraphic

surfaces are defined (e.g., Fig. 4.7), to the ambiguous

291

and sometimes conflicting criteria that are used to

pinpoint surfaces in the rock record. There are histori-

cal reasons why the meaning of the reference curve for

the definition of sequence stratigraphic surfaces is not

fully constrained, and is perhaps even misunderstood,

and these reasons are fully explored in the following

section of this chapter. Conflicting criteria that persist

in the definition of some surfaces also have historical

roots, stemming from deeply entrenched ‘taboos’ in

geological thinking. Many of these deeply rooted prin-

ciples in geology have been re-evaluated in recent years

(e.g., the concept of uniformitarianism, and its impli-

cations for establishing a hierarchy of stratigraphic

cycles––more discussions in Chapter 8; the position of

sequence boundaries in fully fluvial successions relative

to coarse-grained facies––see discussions in Chapter 6;

the relationship between shoreline shifts, sediment

grading and water-depth changes––discussed in

this chapter; the ‘time-barrier’ vs. time-transgressive

character of sequence-bounding unconformities––also

discussed in this chapter, etc.), as afforded by advances

in data acquisition, laboratory techniques, or numerical

modeling.

As discussed above, considerable confusion with

respect to where some of the conformable sequence

stratigraphic surfaces are placed in the rock record is

sourced by alternative approaches to their definition,

such as, for example, the placement of a marine maxi-

mum flooding surface at the top of a ‘fining-upward’

succession or at the top of a ‘deepening-upward’

succession. While such alternative definitions overlap to

some extent, and are traditionally considered as equiva-

lent, a quantitative analysis of the interplay of the

controls on grain size and water-depth changes reveals

that different definition criteria may be satisfied by

discrete surfaces that are spatially offset, as opposed to

pointing to one single surface as intended. This chapter

addresses all these aspects involved in the definition of

sequence stratigraphic surfaces, which have a direct

impact on their temporal attributes, from the ‘master’

reference curve to the criteria employed for mapping

them in the rock record.

REFERENCE CURVE FOR THE

DEFINITION OF STRATIGRAPHIC

SURFACES

The timing of all sequence stratigraphic surfaces

and systems tracts is defined relative to one curve that

describes a full cycle of sea-level, relative sea-level, or

base-level changes, depending on the model that is

being employed (e.g., Figs. 4.7 and 6.1). For example,

the original correlative conformity of Posamentier et al.

(1988) was considered to form during early sea-level

fall (Fig. 6.1), which was later revised to the onset of

sea-level fall (Posamentier et al., 1992b) or the onset of

relative sea-level fall (Posamentier and Allen, 1999).

The correlative conformity of Hunt and Tucker (1992)

is taken at the end of relative sea-level fall (Fig. 6.1),

and so on. Irrespective of the conceptual approach, each

model shows one curve relative to which all surfaces and

systems tracts are defined.

This theoretical curve is generally presented as a

generic sinusoid, with an unspecified position within

the basin. The generic nature of this reference curve

originates from the early seismic and sequence strati-

graphic models of the late 1970s to late 1980s, which

were based on the assumption that eustasy is the

main driving force behind sequence formation at all

levels of stratigraphic cyclicity (Figs. 3.2 and 6.1). Since

eustasy is global in nature, there was no need to spec-

ify where that reference curve is positioned within the

basin under analysis. Subsequent realization in the

1990s, based on much earlier work, that tectonism is

as important as eustasy in controlling stratigraphic

cyclicity, led to the replacement of the eustatic

curve with other reference curves, of relative sea-level

(eustasy plus tectonism) or base-level (relative sea

level plus energy of the depositional environment)

292 7. TIME ATTRIBUTES OF STRATIGRAPHIC SURFACES

Sea level

Base level (fairweather)

Base level (storms)

Sea floor

Datum

water column

sediments

FIGURE 7.1 Concepts of water depth, sea level, relative sea level,

and base level. For the significance of the datum, refer to Chapter 3,

as well as Figs. 3.12 and 3.15. Changes in distances A, B, and C/D

reflect water-depth (bathymetric) changes, relative sea-level changes,

and base-level changes, respectively. Note that the position of the

base level is a function of environmental energy, which marks the

difference between the concepts of relative sea-level and base-level

changes (see also Fig. 3.15). Sea-level changes are independent of

datum, seafloor, and sedimentation, and are measured relative to the

center of Earth.

changes (Figs. 3.15 and 7.1). The shortcoming of these

conceptual advances was that the new reference curves

were still regarded as generic, with an unspecified

position within the basin, despite the fact that subsi-

dence is invariably differential along both dip and strike.

Figure 7.2 presents a dip-oriented cross-section

through a hypothetical basin in an extensional setting,

e.g., a divergent continental margin. In such settings,

subsidence rates vary along dip, increasing towards

the basin (Pitman, 1978; Angevine, 1989; Jordan and

Flemings, 1991). The reference locations A, B, and C are

therefore characterized by different subsidence rates,

as illustrated in Fig. 7.3. Changing subsidence rates

implies that any point within the basin is characterized

by its own curve of relative sea-level/base-level fluc-

tuations (Fig. 7.4), so no one curve is representative for

the entire basin. Due to differences in subsidence rates,

the three curves of relative sea-level changes in Fig. 7.4

are offset relative to one another, not only in terms of

magnitudes but also in terms of timing of the high and

low peaks along the curves. The amount of temporal

offset would be even higher for basins undergoing a

more pronounced differential subsidence. Under these

circumstances, which one of these curves should be

chosen as a reference to define the timing of systems

tracts and bounding surfaces (Fig. 4.7)?

None of the ‘static’ curves (related to specific loca-

tions within the basin) in Fig. 7.4 is the perfect candidate

for the reference curve we need. The curve of relative

sea-level changes at location A, which may approxi-

mate the basin margin, is not suitable because it does

not describe changes in accommodation in the shore-

line region, which have a direct impact on the direction

of shoreline shift. The same applies to the curve that

characterizes location C, which may approximate

the basin center, because this location is again far from

the shoreline region so it does not have a direct control

on the direction of shoreline shift. Location B may offer

the closest approximation for the reference curve, as

being closer to an average shoreline position, but it is

not perfect because with time, the shoreline may move

closer or farther away relative to this location.

Two out of the four main events of a full base-level

cycle refer specifically to changes in the direction of

shoreline shifts, from regression to transgression and

vice versa (Figs. 1.7 and 4.7). Even the other two events,

i.e., the onset and end of base-level fall, are also taken,

irrespective of the sequence model of choice, to signify

a change in the type of shoreline shift, from normal to

forced regression and vice versa, respectively (Fig. 3.19).

Hence, all four main events of the reference curve of

base-level changes are linked to the shoreline, implying

changes in the direction and/or the type of shoreline

shift. What is commonly overlooked is the fact that, as

we move away from the shoreline, changes in base level

recorded in other locations may differ significantly

from the reference curve that describes changes in the

direction and/or the type of shoreline shift. For example,

a forced regression (base-level fall at the shoreline)

may well be coeval with a base-level rise offshore, due

to variations in subsidence rates (the case envisaged by

Vail et al., 1984, for the formation of ‘type 2’ sequence

boundaries), and so on (Figs. 7.2–7.4). This means that

the curves of base-level changes that characterize

discrete locations within the basin are offset relative to

one another, as explained above (Fig. 7.4), which requires

us to specify where exactly along each dip-oriented

section the reference curve of base-level changes is

taken.

The shoreline is dynamic, as it continuously changes

its position within the basin as a function of the local

balance between accommodation and sedimentation.

The reference curve of base-level shifts should therefore

describe the changes in accommodation at the shoreline,

wherever the shoreline is within the basin at each time

step. This means that the actual shifts in base level

along the reference curve, in terms of magnitude and

timing, can be quantified by interpolating between the

‘static’ A, B, and C curves, according to the location of

the shoreline at every time step.

REFERENCE CURVE FOR THE DEFINITION OF STRATIGRAPHIC SURFACES 293

300

(m)

(Km)

ABC

Sea level

Fluvial environment Marine environment

Shoreline

Pre-existing

stratigraphic succession

FIGURE 7.2 Dip-oriented cross-

section through a hypothetical exten-

sional basin. Locations A, B, and C

are characterized by different subsi-

dence rates, as illustrated in Fig. 7.3.

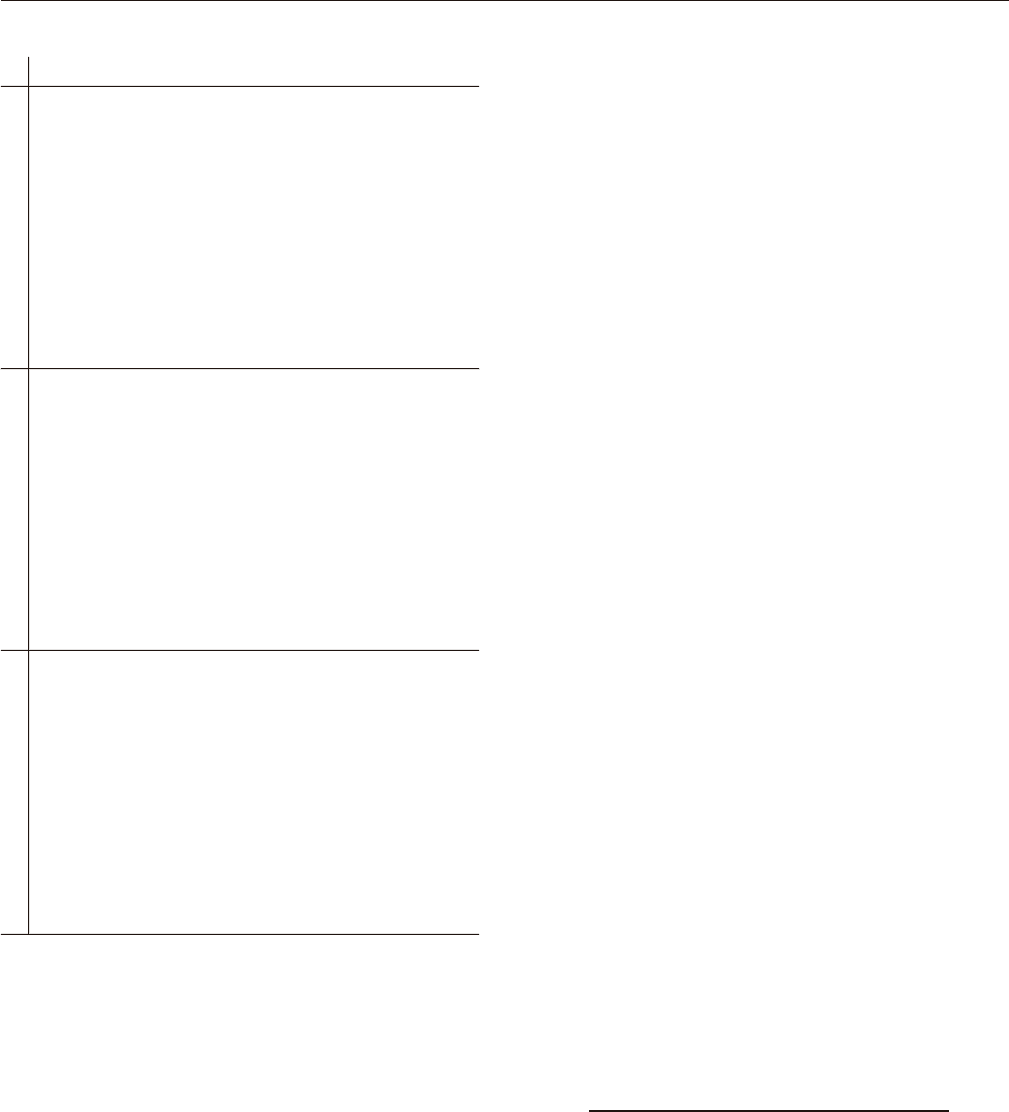
A forward modeling simulation, based on the data

shown in Figs. 7.2–7.4 helps to illustrate these points.

Starting from the initial reference profile in Fig. 7.2, and

based on the sea level and subsidence data in Fig. 7.3,

the stratigraphic architecture is gradually built for the

15 time steps, as illustrated in Figs. 7.5–7.8. The sediment

supply is not quantified in this forward simulation, but

is maintained constant through time by assigning the

same volume of sediment to all depositional wedges

that form at different time steps. The newly accumulated

sedimentary wedge of each time slice is marked with

grey on the forward modeling diagrams (Figs. 7.5–7.8),

and includes fluvial, coastal, and undifferentiated

shallow- to deep-water facies. The amount of accom-

modation created or destroyed at the shoreline during

each time slice was calculated by interpolation

between profiles A and B, or B and C, depending on

the location of the shoreline during that particular

time interval. This amount of available accommodation

is critical to establish how much aggradation or erosion

takes place at the shoreline during each time step,

which also has a direct influence on the rates of progra-

dation or retrogradation. The types of shoreline shifts

are marked on the cross-sections, and the differential

subsidence was taken into account by gradually tilting

the profile from one time step to another accordingly.

The final stratigraphic architecture and facies relation-

ships are shown in Fig. 7.9.

Figure 7.10 illustrates the curve of relative sea-level

changes at the shoreline, which was obtained by inter-

polation between the curves that characterize locations

A, B, and C (Figs. 7.2–7.4), according to the shoreline

position at every time step. This is the reference curve

that sequence stratigraphic models are centered around,

which describes changes in accommodation at the

shoreline. The interplay between sedimentation and this

curve of base-level changes controls the transgressive

and regressive shifts of the shoreline, as marked in the

diagram, and implicitly the timing of all systems

tracts and bounding surfaces. This reference curve is

‘dynamic,’ as it follows the shoreline in its shifts

back and forth along the dip-oriented cross-section, as

opposed to the ‘static’ curves of specific locations

(e.g., A, B, and C in Fig. 7.2).

SHORELINE SHIFTS, GRADING,

AND BATHYMETRY

Controls on Sediment Grading

and Water-depth Changes

In addition to understanding the meaning of the

reference curve of relative sea-level changes (Fig. 7.10), it

is also important to observe the bathymetric trends in

different locations within the basin during the transgres-

sive and regressive shifts of the shoreline. As discussed

in more detail in Chapter 3, water depth at any loca-

tion within the marine basin depends on the interplay

294 7. TIME ATTRIBUTES OF STRATIGRAPHIC SURFACES

0 to 1

1 to 2

2 to 3

3 to 4

4 to 5

5 to 6

6 to 7

7 to 8

8 to 9

9 to 10

10 to 11

11 to 12

12 to 13

13 to 14

14 to 15

0 to 1

1 to 2

2 to 3

3 to 4

4 to 5

5 to 6

6 to 7

7 to 8

8 to 9

9 to 10

10 to 11

11 to 12

12 to 13

13 to 14

14 to 15

0 to 1

1 to 2

2 to 3

3 to 4

4 to 5

5 to 6

6 to 7

7 to 8

8 to 9

9 to 10

10 to 11

11 to 12

12 to 13

13 to 14

14 to 15

−20

−30

−20

−5

−20

−30

−20

−5

−20

−30

−20

−5

−15

−25

−15

−20

−30

−20

−5

−10

Time* - ∆ Subsidence

= Σ RSL

∆ Eustasy

∆ RSL

−5

105

130

145

150

−10

−20

−10

100

120

160

190

210

220

225

Location A in Figure 7.2Location B in Figure 7.2Location C in Figure 7.2

FIGURE 7.3 Changes in sea level, subsidence, and relative sea

level along the profile in Fig. 7.2, during a period of time of 1.5 Ma

(modified from data provided by H. W. Posamentier). Incremental

changes in sea level, subsidence, relative sea level, and cumulative

relative sea level are shown for time steps of 100.000 years. The

curve of sea-level changes is the same for the three reference loca-

tions in Fig. 7.2. Subsidence rates increase towards the basin, and are

considered to be stable during the 1.5 Ma time interval: 0 m/10

years for location A, 5 m/10

years for location B, and 10 m/10

years for location C. Eustasy combined with subsidence allows for

the calculation of the relative sea-level change (∆ RSL) for each time

step. The cumulative relative sea level (Σ RSL) is calculated in the

last column of the table. Key: * (x 10

years),

m/10

years,

0123456789101112131415

380

360

340

320

300

280

260

240

220

200

180

160

140

120

100

−20

−40

−60

−80

−100

−120

−140

−160

−180

Time (× 10

years)

Meters Above and Below Reference Position at Time 0

RSL (Subsidence = −10 m/10

years)

RSL (Subsidence = −5 m/10

years)

RSL=Eustasy (zero subsidence)

Subsidence=0 m/10

years

Subsidence=−5 m/10

years

Subsidence=−10 m/10

years

FIGURE 7.4 Subsidence, eustatic, and

relative sea-level curves plotted based

on the data provided in Fig. 7.3, for the

1.5 Ma time interval (modified from

data provided by H. W. Posamentier).

Note that for location A (Figs. 7.2 and 7.3),

where subsidence is zero, the sea-level

curve coincides with the relative sea-level

curve. For locations B and C (Figs. 7.2 and

7.3), the relative sea-level curves account

for the combined effects of eustasy and

subsidence.

300

Shoreline at time 0

(m)

(Km)

ABC

Time step 1

Time step 2

Time step 3

Time step 0

Sea level (1)

(normal regression)

Sea level (2)

Sea level (3)

previous profile, subject to differential subsidence

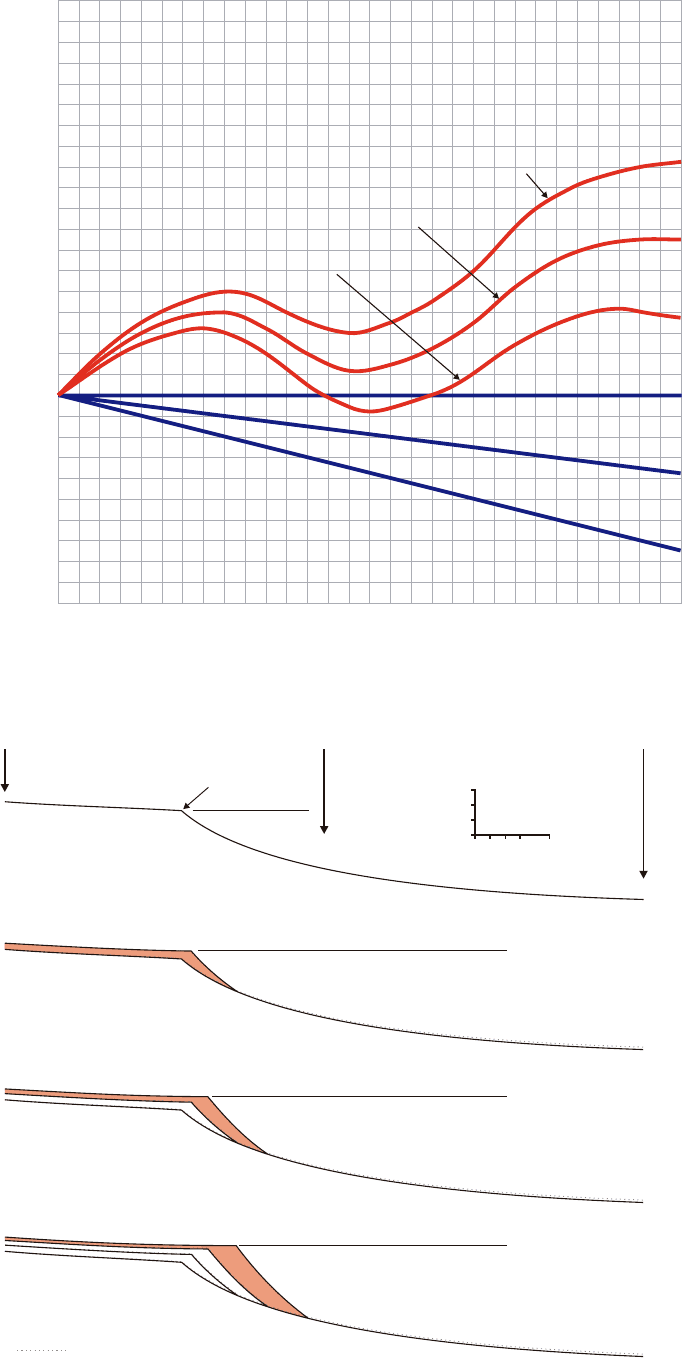
FIGURE 7.5 Forward modeling simulation

(time steps 1–3) based on the data provided in

Figs. 7.2–7.4. See text for additional explana-

tions. Note that the amount of accommodation

that is being created at the shoreline decreases

with time, which triggers an increase in the

progradation rates. This amount of accommo-

dation is calculated by interpolation between

the relative sea-level curves at locations A and

B (Fig. 7.4), according to the position of the

shoreline during each time slice. Each cross-

section is tilted relative to the previous one

according to the rates of differential subsi-

dence. All facies prograde in relation to the

basinward shift of the shoreline.

300

(m)

(Km)

ABC

Time step 4

Time step 5

Time step 6

Time step 7

Sea level (4)

(normal regression)

Sea level (5)

(forced regression)

Sea level (6)

(forced regression)

Sea level (7)

(forced regression)

subaerial unconformity

basal surface of forced regression

previous profile, subject to tilt and erosion

Submarine fan complex

FIGURE 7.6 Forward modeling simulation (time steps

4–7) based on the data provided in Figs. 7.2–7.4. See text

for additional explanations. Note that the top of the

normal regressive deposits is subject to erosion during the

forced regression of the shoreline. As a result, the subaer-

ial unconformity forms. The amount of erosion at the

shoreline is calculated by interpolation between the rela-

tive sea-level curves at locations A and B (Fig. 7.4),

according to the position of the shoreline during each

time slice. Each cross-section is tilted relative to the previ-

ous one according to the rates of differential subsidence.

No offlapping shallow-marine facies are represented, for

simplicity.

300

(m)

(Km)

ABC

Sea level (8)

(normal regression)

Sea level (9)

Sea level (10)

(normal regression)

(transgression)

Sea level (11)

(transgression)

Time step 8

Time step 9

Time step 10

Time step 11

subaerial unconformity

basal surface of forced regression

previous profile, subject to differential subsidence

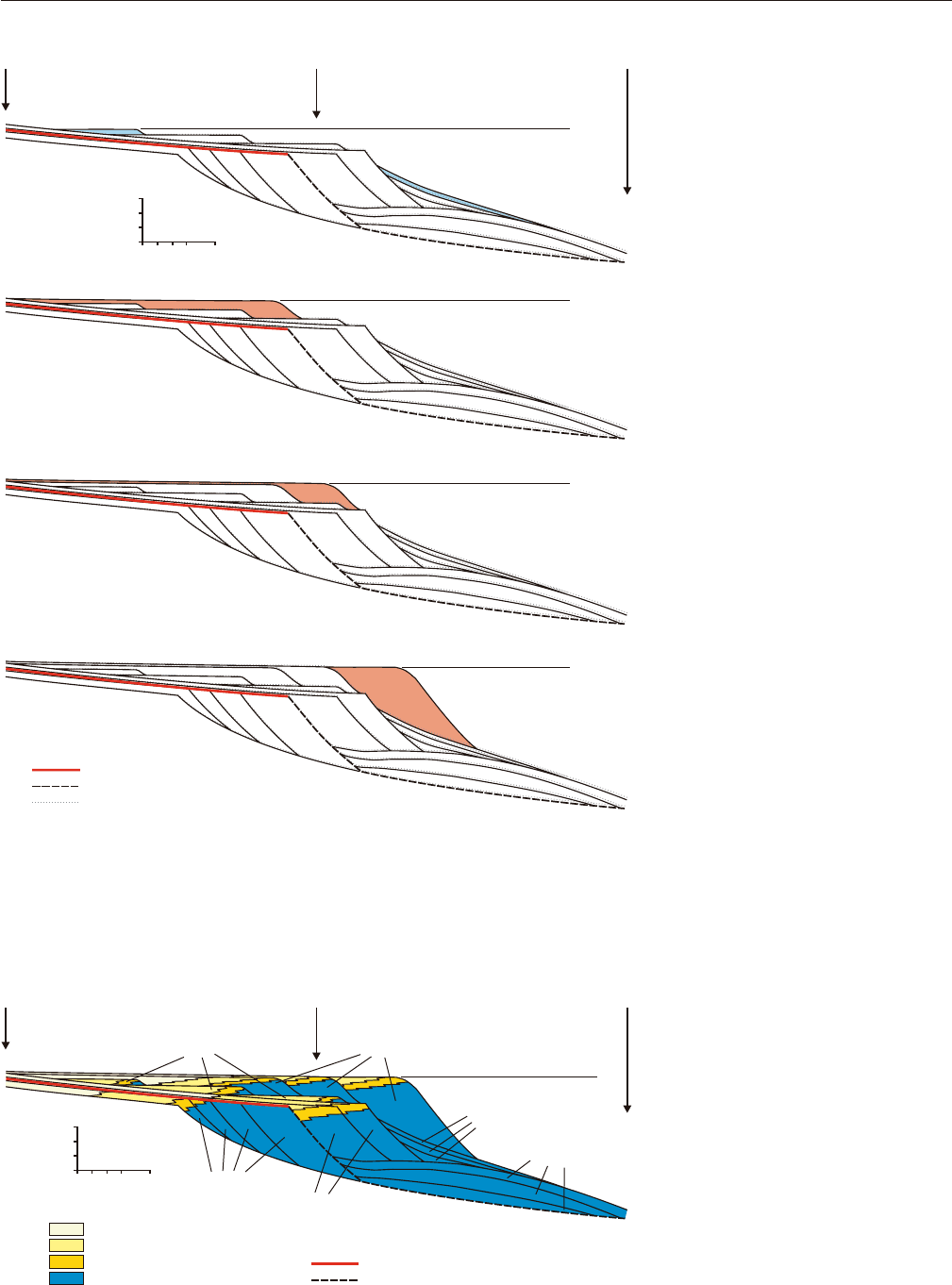
FIGURE 7.7 Forward modeling simulation (time

steps 8–11) based on the data provided in Figs. 7.2–7.4.

See text for additional explanations. Note that the change

from normal regression (time steps 8 and 9) to transgres-

sion (time steps 10 and 11) depends on the interplay of

sedimentation and accommodation at the shoreline. Since

sediment supply is not quantified in this exercise, the

transgression was arbitrarily selected to start with time

step 10, because of the accelerated rates of base-level rise

noted in Fig. 7.4. The amount of available accommodation

at the shoreline is calculated by interpolation between the

relative sea-level curves at locations A, B, and C (Fig. 7.4),

according to the position of the shoreline during each

time slice. Each cross-section is tilted relative to the previ-

ous one according to the rates of differential subsidence.

The rates of progradation and retrogradation change

with time, and are linked to the rates of creation of accom-

modation at the shoreline: the lower the accommodation

at the shoreline, the higher the progradation rates; the

higher the accommodation at the shoreline, the higher the

retrogradation rates.

of subsidence, sea-level change, and sedimentation.

Subsidence and sea-level rise contribute towards water

deepening, whereas sea-level fall and sedimentation

promote water shallowing. In contrast, sediment grad-

ing trends that develop during the same transgressive

and regressive shifts of the shoreline are controlled by

a different set of parameters, which may be independ-

ent of water depth, namely sediment supply and depo-

sitional energy. This section examines the intricate

relationship between shoreline shifts, grading, and

SHORELINE SHIFTS, GRADING, AND BATHYMETRY 297

300

(m)

(Km)

A C

Sea level (12)

Sea level (13)

(transgression)

(normal regression)

Sea level (14)

(normal regression)

Sea level (15)

Time step 12

Time step 13

Time step 14

Time step 15

subaerial unconformity

basal surface of forced regression

previous profile, subject to differential subsidence

FIGURE 7.8 Forward modeling simula-

tion (time steps 12–15) based on the data

provided in Figs. 7.2–7.4. See text for addi-

tional explanations. Note that the change

from transgression (time step 12) to normal

regression (time steps 13 to 15) depends on

the interplay of sedimentation and accom-

modation at the shoreline. Since sediment

supply is not quantified in this exercise, the

normal regression was arbitrarily selected

to start with time step 13, because of the

lower rates of base-level rise noted in Fig. 7.4.

The amount of available accommodation at

the shoreline is calculated by interpolation

between the relative sea-level curves at

locations A, B, and C (Fig. 7.4), according to

the position of the shoreline during each

time slice. Each cross-section is tilted rela-

tive to the previous one according to the

rates of differential subsidence. The rates of

progradation and retrogradation change

with time, and are linked to the rates of

creation of accommodation at the shoreline:

the lower the accommodation at the shore-

line, the higher the progradation rates; the

higher the accommodation at the shoreline,

the higher the retrogradation rates.

300

(m)

(Km)

ABC

Sea level

subaerial unconformity

basal surface of forced regression

Submarine fan complex

(FSST)

Transgressive wedges

(“marine onlap”)

HST 1

LST

TST

HST 2

fluvial (proximal)

fluvial (distal)/delta plain

coastal

shallow to deep marine

FIGURE 7.9 Stratigraphic architecture of

the succession modeled in Figs. 7.5–7.8

(modified from data provided by

H. W. Posamentier). Abbreviations: LST––

lowstand systems tract; TST––transgressive

systems tract; HST––highstand systems

tract; FSST––falling-stage systems tract.

298 7. TIME ATTRIBUTES OF STRATIGRAPHIC SURFACES

Relative Sea Level at the Shoreline (m)

Rise (+)

280

260

240

220

200

180

160

140

120

100

−20

−40

−60

−80

−100

−120

−140

−160

−180

Time (× 10

years)

0123456789101112131415

Fall (−)

** =correlative conformity sensu Posamentier et al. (1988)

sensu Hunt and Tucker (1992)

Normal

regression

(LST)

Forced

regression

(FSST)

Normal

regression

(HST)

Transgression

(TST)

Normal

regression

(HST)

Subaerial

unconformity

and

Regressive surface

of marine erosion

Maximum

regressive

surface

Maximum

flooding

surface

Ravinement

surface

Basal surface of

forced regression

Correlative

conformity

FIGURE 7.10 Reference curve of relative sea-level changes for the stratigraphic succession in Fig. 7.9.

This curve indicates changes in accommodation at the shoreline, as the shoreline transgresses and regresses

with time. It is therefore a ‘dynamic’ curve, depicting the accommodation budget at different locations

through time. It is the interplay of this reference curve and sedimentation that dictates the timing of all

systems tracts and bounding surfaces.

bathymetry, and the extent of the correlation between

the latter two variables during stages of shoreline

transgression or regression.

Figure 7.11 shows two curves of water-depth

changes in two specified locations, for the 15 time steps

of the forward model run. Water depth is calculated as

the vertical distance between the sea level and the

seafloor at each time step. Note that the transgression

of the shoreline can be safely associated with water

deepening in the basin, assuming that subsidence rates

increase, and sedimentation rates decrease, in a basin-

ward direction. This is usually the norm in divergent-

type settings, as considered in this forward modeling

simulation. The normal regression of the shoreline is

coeval with water shallowing in the vicinity of the shore-

line, and with water deepening offshore, based on the

same assumptions as above. The forced regression

of the shoreline corresponds to water shallowing in

Fig. 7.11, but it may also be coeval with water deepen-

ing beyond the submarine fan or in the absence of a

well-developed submarine fan, depending on the subsi-

dence rates offshore. Under differential subsidence

conditions, it is conceivable that low subsidence rates

may be outpaced by eustatic fall at the shoreline (base-

level fall, and forced regression of the shoreline, result-

ing in water shallowing in the vicinity of the shoreline),

whereas higher subsidence rates may outpace the sum

of eustatic fall and sedimentation offshore (hence water

deepening beyond a point of balance between subsi-

dence, sea-level fall and sedimentation).

So what is the relationship between shoreline shifts,

grading of marine deposits, and water-depth changes?

We can take as an example the normal regressive delta

that progrades into the basin between time steps 1

and 4 (Fig. 7.11). Sediment entry points shift towards

the basin during this time interval, so the succession is

coarsening upward, from offshore pelagic (time step 1)

to prodelta (time step 2) to delta front deposits (time

steps 3 and 4) (reference location 1 in Fig. 7.11). Prodelta

facies (thin bottomset, not represented in Fig. 7.11 for

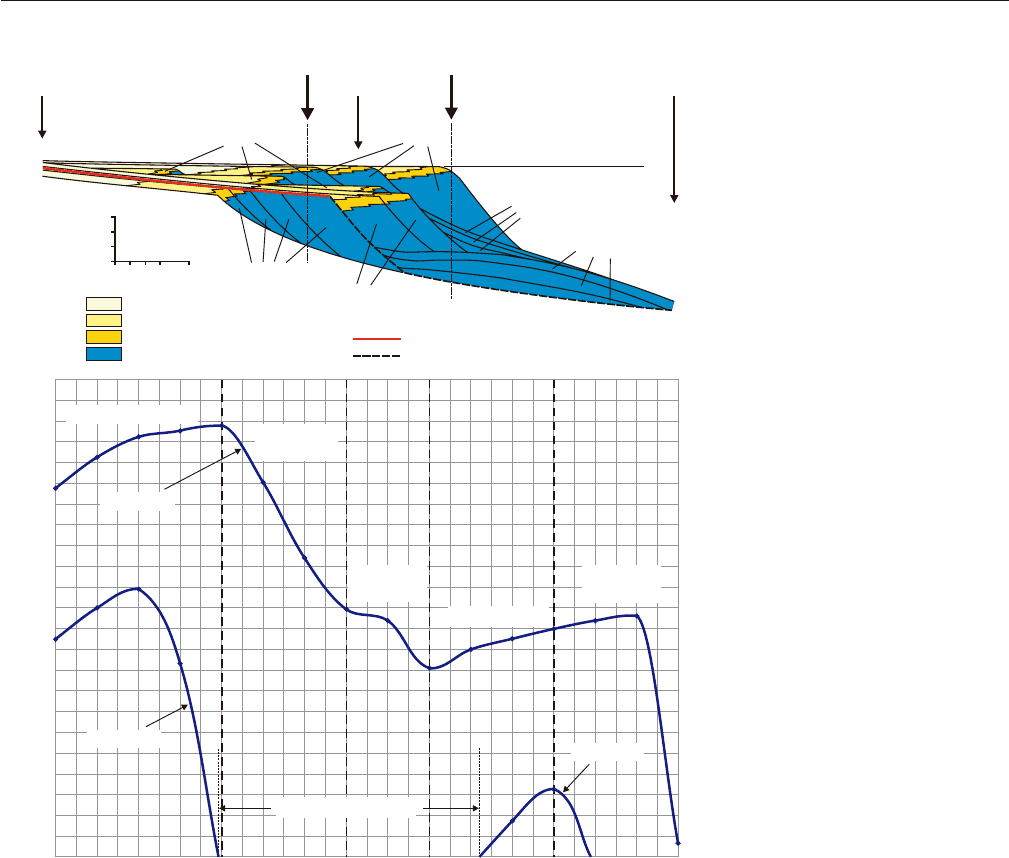
simplicity) are characterized by the presence of silt-size

riverborn sediments, which gradually prograde over

the finer pelagic basinal facies. In turn, the silty prodelta

sediments are prograded by the sand-dominated delta

front facies, which generates the overall coarsening-

upward trend. At the same time, the bathymetric profile

shows a deepening of the water during time steps 1

and 2, followed by shallowing as soon as the point of

observation (location 1 in Fig. 7.11) becomes part of the

subtidal (delta front) environment. The deepening of

the water during the deposition of shelf and overlying

prodelta facies (time steps 1 and 2) is due to the fact

that sedimentation rates are too low to keep up with the

rates of creation of accommodation. For time steps 3

and 4, the shallowing of the water is driven by the much

higher sedimentation rates in the delta front environ-

ment, which outpace the rates of base-level rise. This

example shows that the water-depth/grain-size rela-

tionship is not necessarily linear, as commonly assumed,

meaning that an increase in water depth does not have

to be accompanied by a decrease in size of the sediment

delivered to that particular location.

The generally assumed linear relationship between

water depth, depositional energy, and grain size is

modified by other parameters such as slope (gradient

of seafloor) and the associated gravity-driven

subaqueous flows (Figs. 6.15, 7.12, and 7.13), and, most

importantly, by changes in sediment supply associated

SHORELINE SHIFTS, GRADING, AND BATHYMETRY 299

300

(m)

(Km)

ABC

Sea level

subaerial unconformity

basal surface of forced regression

Submarine fan complex

(FSST)

Transgressive wedges

("marine onlap")

HST 1

LST

TST

HST 2

fluvial (proximal)

fluvial (distal)/delta plain

coastal

shallow to deep marine

Water Depth (m)

0123456789101112131415

460

440

420

400

380

360

340

320

300

280

260

240

220

200

180

160

140

120

100

Time (× 10

years)

Location 1

Location 2

Location 1

Forced

Regression

Normal

Regression

Normal

Regression

Transgression

Subaerial Exposure

Normal Regression

Location 2

FIGURE 7.11 Water-depth changes

through time, at locations 1 and 2 indi-

cated on the cross-section. See text for

explanations. Abbreviations: LST––

lowstand systems tract; TST––transgressive

systems tract; HST––highstand systems

tract; FSST––falling-stage systems tract.