Casing/Tubing design manual october 2005 Chevron

Подождите немного. Документ загружается.

Casing/Tubing Design Manual 13-17

October 2005

13.13.2 Buckling Effect

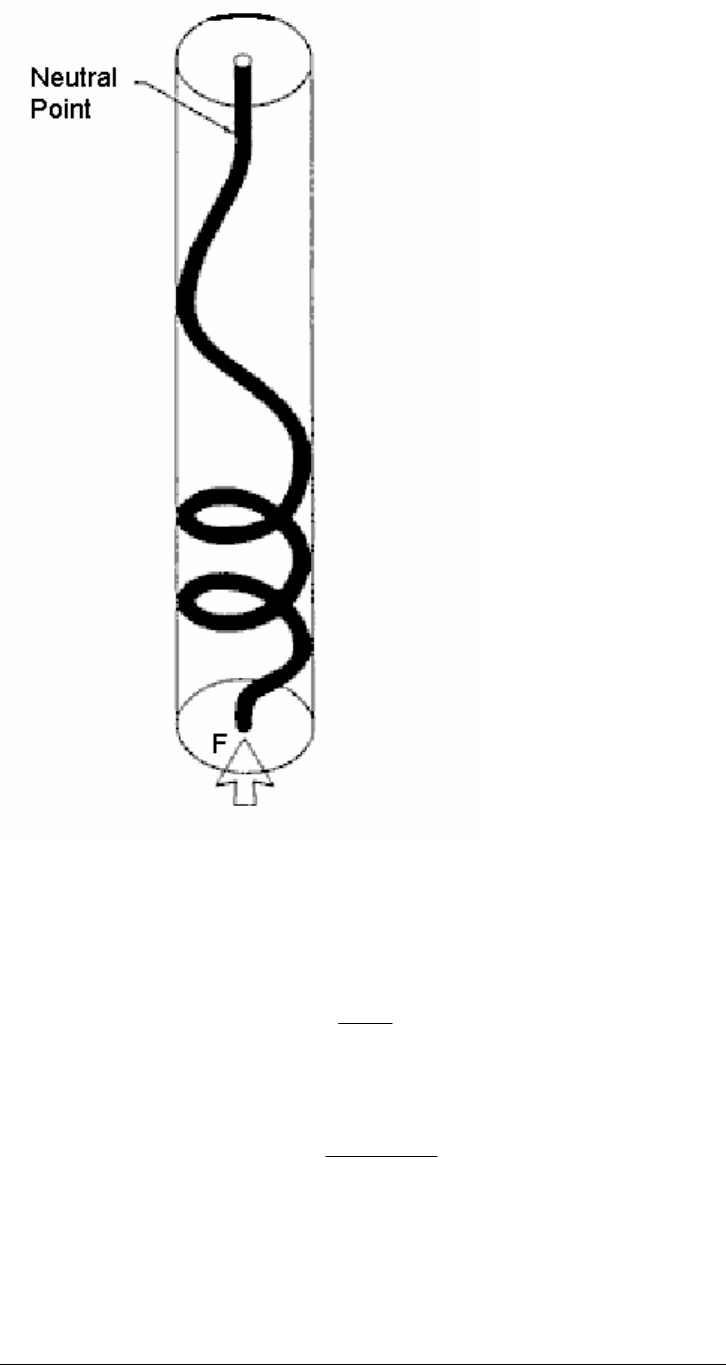
Helical buckling is initiated by compressive force acting on the bottom of the

tubing and is the formation of helical spirals in the tubing string. The helix shown

in Figure 13-8 has a variable pitch as the compressive force is progressively

lowered by the weight of the pipe hanging below.

The buckling effect is greater when pressure differential is applied across the

pipe. Unless the tubing string is short or the compressive force is exceedingly

high, some of the tubing will be buckled and the rest straight. The exact point

between the buckled and straight sections is the “neutral point” (refer to Figure

13-8).

The neutral point can be calculated from the following:

N = F/W (13-5)

where:

W = Ws + Wi - Wo

Wi = Ai x Weight of fluid inside the tubing

Wo = Ao x Weight of fluid outside the tubing

13-18 Casing/Tubing Design Manual

October 2005

Figure 13-8. Neutral Point

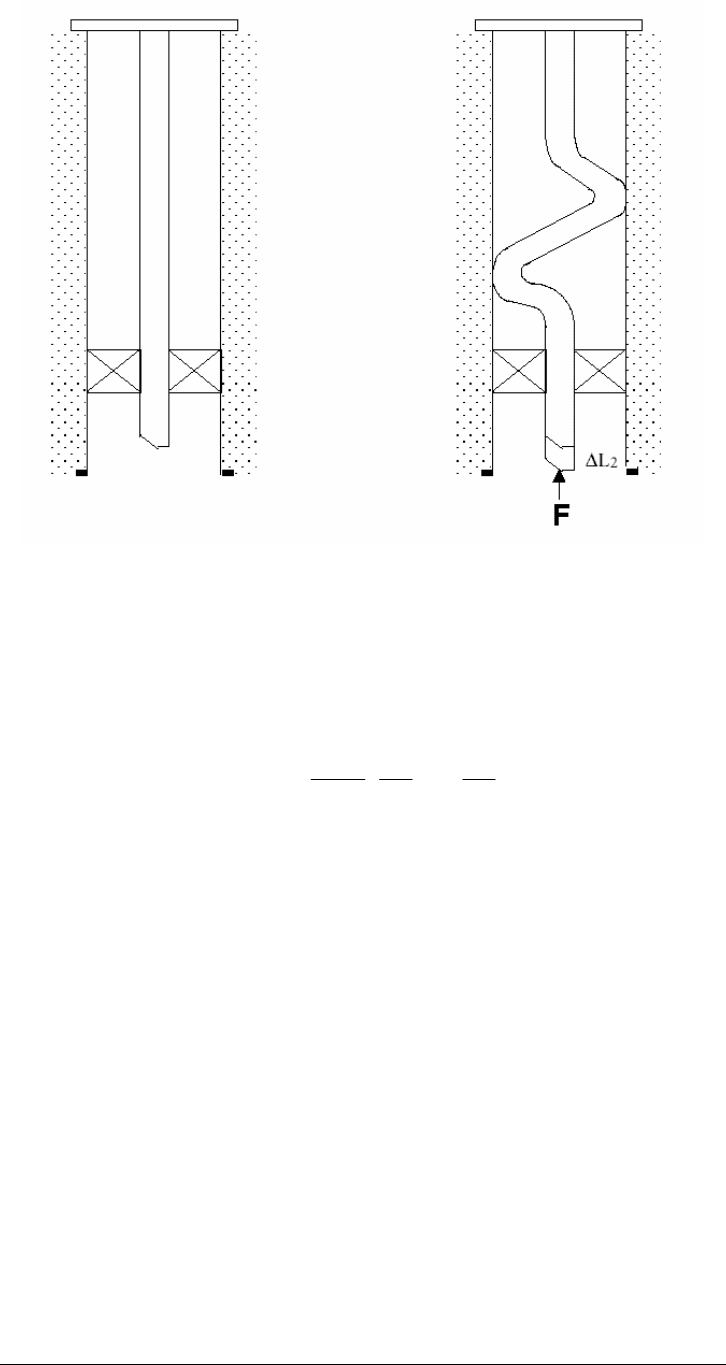
When the neutral point is within the tubing length (and so the helix can fully

develop), the length reduction because of helical buckling (refer to Figure 13-9)

can be calculated by the following formula:

EIw

=Λ

(13-6)

Where:

(

)

−

Casing/Tubing Design Manual 13-19

October 2005

Figure 13-9. Helical Buckling

If the tubing is very short (as happens, for example, on selective type

completions between two packers) all the string may be affected by buckling and

there is no neutral point. In this case, the length reduction because of the

buckling effect is dependant upon the entire length of the string and can be

calculated by the following formula:

n > L

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−=Λ

EIw

L 2

(13-7)

As seen, the formulae for both piston affect and the helicoidal buckling above

have used F, i.e. the change in the piston force acting on the bottom of the

tubing. However, in order to complete the understanding of the effects which lead

to variations in length because of buckling, we must also consider the effect

caused by pressure differential across a pipe.

If the internal pressure in a pipe is greater than the external pressure, the tube

remains straight only if it has an axially symmetric cross section with no

deformation to change its shape. This configuration is unstable and any distortion

can lead immediately to a stable equilibrium condition, which is helicoidal

buckling.

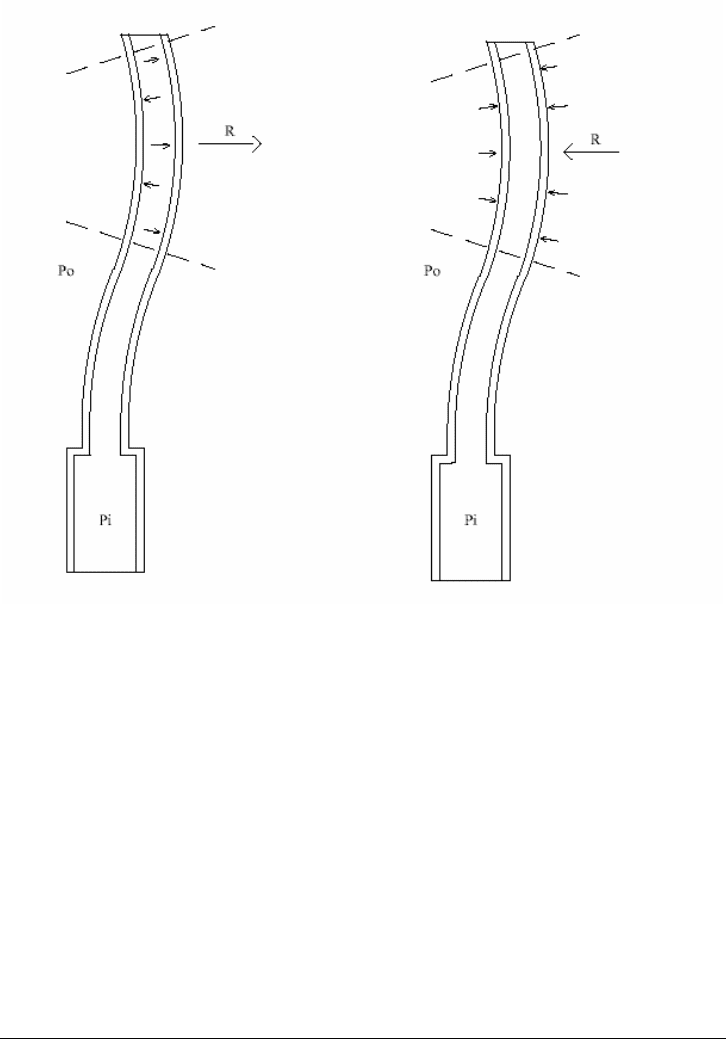
Helicoidal buckling is caused by the affect of the pressure, which acts on the

lateral surface of the pipe wall as the convex surface of the bend in a greater

force is larger than the concave surface (refer to Figure 13-9). The internal

pressure will, therefore, exert a greater force on the convex side of the helix than

that exerted on the concave section of the same bend. Therefore, the resulting

force will create the helicoidal buckling configuration.

13-20 Casing/Tubing Design Manual

October 2005

The same configuration occurs when the stable external pressure is greater than

the internal pressure also resulting in helical buckling. Moreover, the affect of the

external pressure on the tubing lateral surfaces is equivalent to a tensile force

applied at the tubing bottom of:

PAF =

(13-8)

PAF −=

(13-9)

Internal pressure External pressure

Figure 13-10. Pressure-Induced Helical Buckling Effect

From this it can be concluded that the effect of the internal pressure on the tubing

lateral surfaces is equivalent to a compressive force applied at the bottom of the

tubing. Therefore, the tubing will be buckled by the piston force and by the sum

of Ff 1 and Ff 2. The fictitious force Ff is obtained from the sum of the three

elements:

FFFF ++=

(13-10)

By substitution:

(

)

oipf

PPAF

−

(13-11)

Casing/Tubing Design Manual 13-21

October 2005

If Ff is greater than zero, it will cause helical buckling and, hence, if it is less than

zero there is no deformation. It is however important to relate that the only force

actually applied at the bottom of the tubing is the piston force, while the fictitious

force is used only to calculate the buckling effect.

It should be remembered that to calculate the variations in length, the variations

of the forces compared to initial conditions must be calculated. Therefore, in

summation:

• In the ∆L1 (Hooke’s law), the variation of the piston force Fa must be

used.

• In the ∆L2 (buckling), the variation of the fictitious force Ff must be used

when this is positive; otherwise, being a tensile force, it cannot buckle

the string and ∆L2 = 0.

The theory above was developed considering Pi = Po in the initial conditions, it

thus follows that the Ff is equal to zero and that the variation of fictitious force ∆Ff

is equal to the final fictitious force.

13.13.3 Ballooning Effect

The third element which changes the length of a string because of the changes

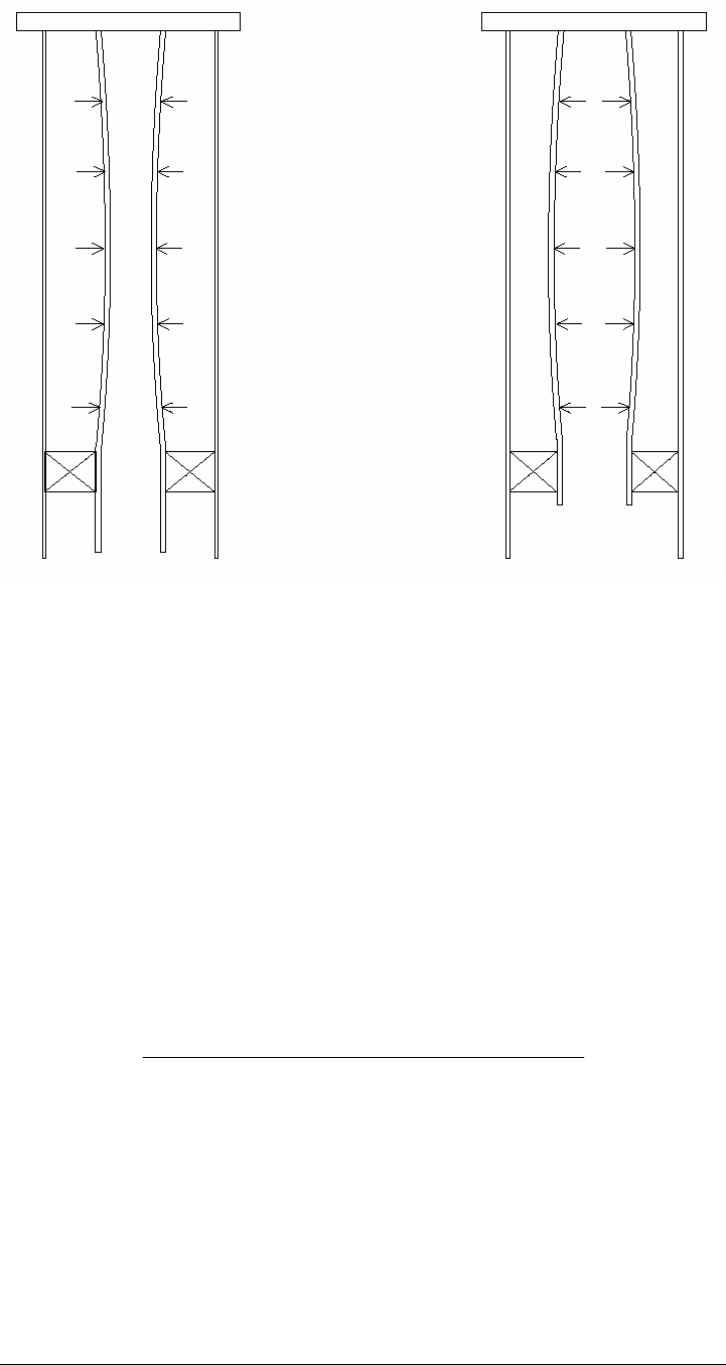
to internal and external pressure is caused by ballooning. This effect occurs

when ∆P = Pi - Po is positive and tends to swell the tubing, which contracts

axially or shortens. Conversely, when ∆P = Pi - Po is negative, the tubing is

squeezed and expands axially or elongates. This is termed reverse ballooning

(refer to Figure 13-11).

The normally used simplified formula to calculate the ballooning or reverse

ballooning effect is:

PRP

omim

⎟

⎠

⎞

⎜

⎝

⎛

−

Λ−Λ

⎟

⎠

⎞

⎜

⎝

⎛

−=Λ

(13-12)

In this the average internal and external pressure variations are defined by the

formulae:

[

]

[

]

()(()(

bottomhole

initialifinali

tophole

initialifinali

PPPP

−

=Λ

(13-13)

[

]

[

]

)()()()(

bottomhole

initialofinalo

tophole

initialofinalo

PPPP

−

=Λ

(13-14)

They are developed from Hooke’s law by using Young’s modulus of elasticity

(used in the piston and buckling effect) and Poisson’s ratio.

Poisson’s ratio “v” as earlier expressed is:

13-22 Casing/Tubing Design Manual

October 2005

Figure 13-11. Reverse Ballooning or Ballooning

13.13.4 Temperature Effect

The final effect considered when calculating tubing length variations, is the

temperature effect which usually induces the largest movement. During a well

operation, e.g., stimulation, the temperature of the tubing may be much less than

that in the initial or flow rate conditions. In well stimulations, significant quantities

of fluids are pumped through the tubing at ambient surface temperature, which

may change the temperature of the tubing by several degrees.

The formula used to calculate the change of length due to temperature effect is:

LTL

(13-15)

Where the average temperature variation in the string can be calculated by:

[

]

[

]

)()()()(

bottomhole

initialfinal

tophole

initialfinal

TTTT

−

=Λ

(13-16)

In the formula, α represents the material’s coefficient of thermal expansion. For

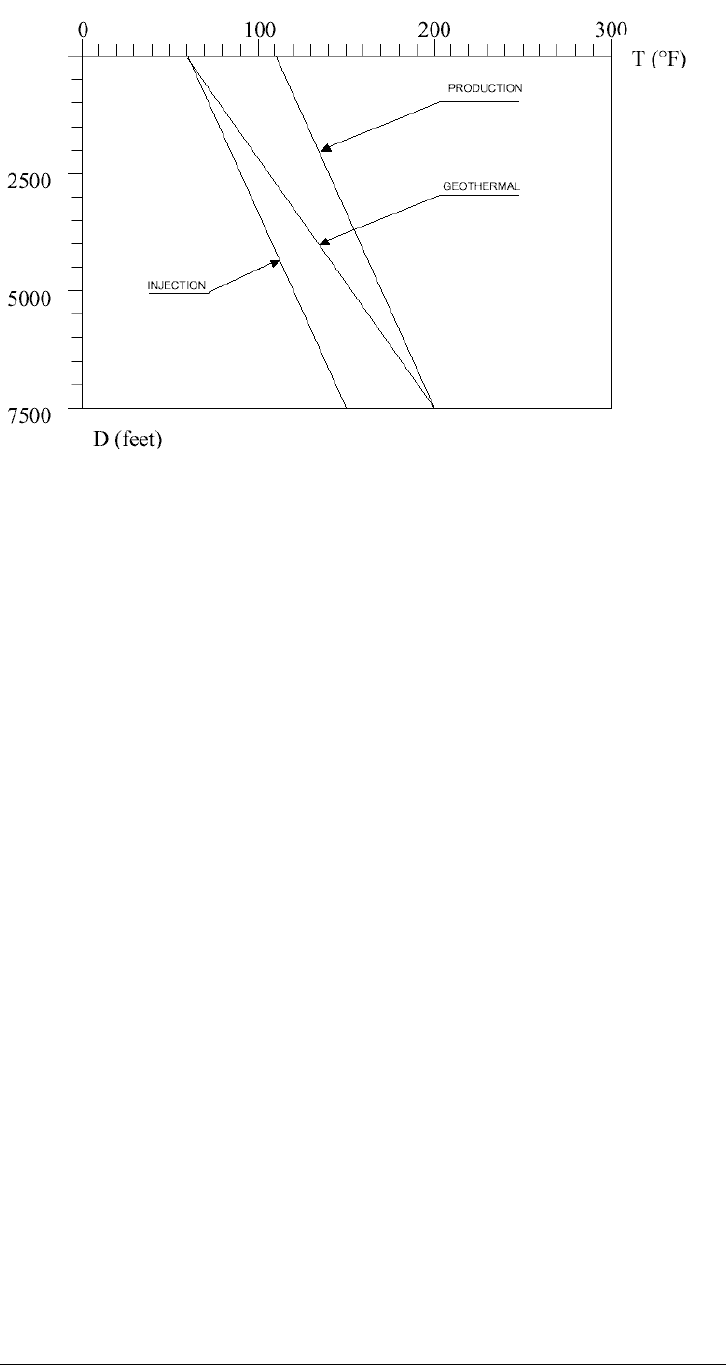
steel this value is: α = 6.9 x 10-6 in/in/°F. Figure 13-12 shows typical geothermal

temperature gradients during stimulation and production conditions. It can be

seen that the temperature variations to which the tubing is subjected may cause

considerable changes to its length.

Casing/Tubing Design Manual 13-23

October 2005

Figure 13-12. Typical Geothermal Gradients

13.14 Evaluation of Total Length Change

The sum of the length changes obtained from the changes in pressure-induced

forces and temperature effects gives the total shift of the bottom end of the string

at the packer depth where it is free to move in the packer-bore. This sum is

calculated:

∆

Ltot =

∆

L1 +

∆

L2 +

∆

L3 +

∆

L4 (13-17)

With free moving packer/tubing seals systems, the calculations are made for the

selection of an appropriate length of seal assembly, PBR or ELTSR, with

anchored packer/tubing systems. This calculation can be made to select the

length of tubing movement devices, such as telescopic or expansion joints.

However, if no movement is converted to stress in the tubing, the resultant is

stress on the packer.

13.15 Tubing to Packer and Packer to

Casing Force

13.15.1 Anchored Tubing

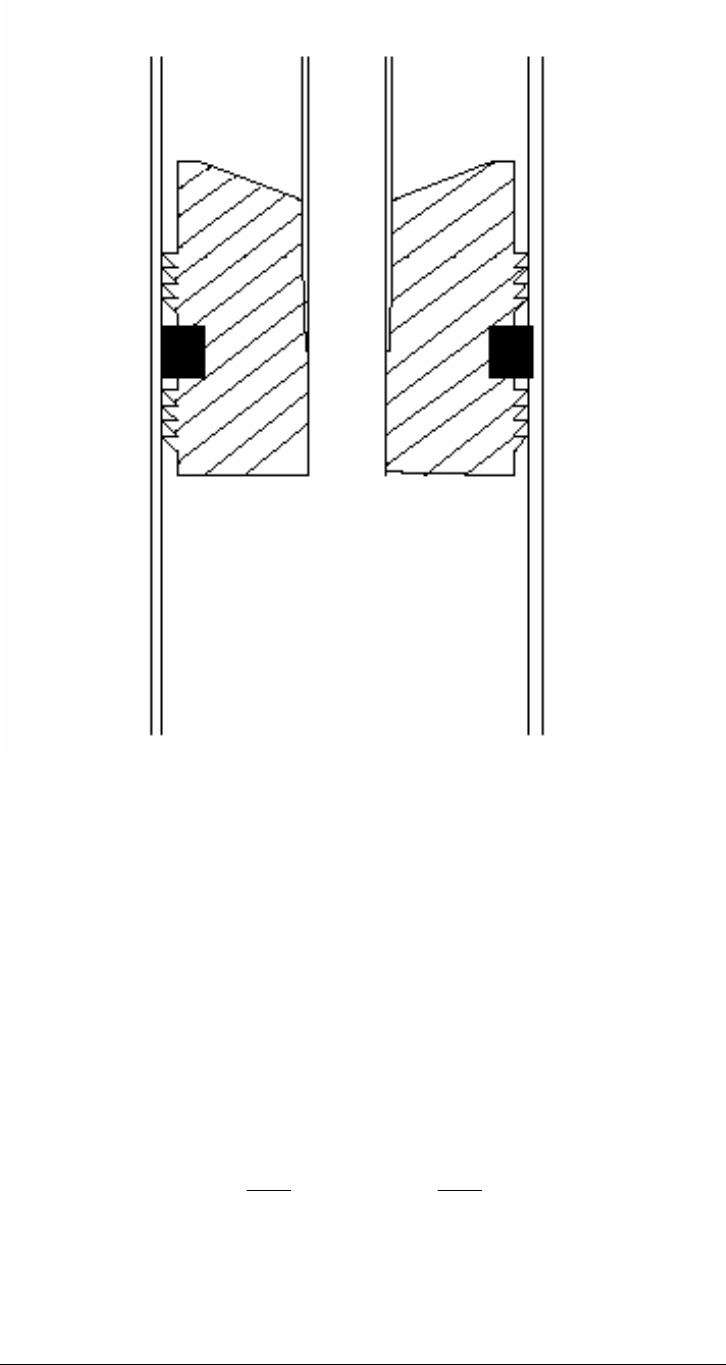
In some completions, the tubing is firmly fixed to the packer, preventing any

movement of the string when well conditions vary (see Figure 13-13). In this

situation the tubing-packer forces generated by the presence of the anchoring

must be determined to confirm if the tubing-packer anchoring system and the

packer have sufficient strength to safely withstand all the forces exerted.

Moreover, after this force is known, the load on the tubing can be calculated to

check if the completion components have sufficient strength.

13-24 Casing/Tubing Design Manual

October 2005

Figure 13-13. Tubing Anchored to Packer

The tubing-packer force can be calculated by initially assuming that the tubing is

free to move in the packer seal-bore and it is possible to calculate the final total

length change of the tubing under pressure and temperature variations of all

conditions. Subsequently, the force needed to re-anchor the tubing to the packer

can be determined.

To understand this concept better, consider Figure 13-13 where it is presumed

that the tubing can move away from its anchored condition while maintaining the

seal with the packer and that the tubing undergoes only ∆L4 contraction caused

by the temperature effect. Because no force is applied at the end of the tubing

which could cause buckling, all the movement is linear and to restore to the

tubing’s real anchored position, it is sufficient to impose a ∆L4 elongation by

applying a force FP, which is obtained from Hooke’s law:

Λ−=⇒−=Λ (13-18)

However, in general, the problem of identifying the tubing/packer reaction is not

linear due to the helical buckling effect and so it is possible to use a graphical

approach.

Casing/Tubing Design Manual 13-25

October 2005

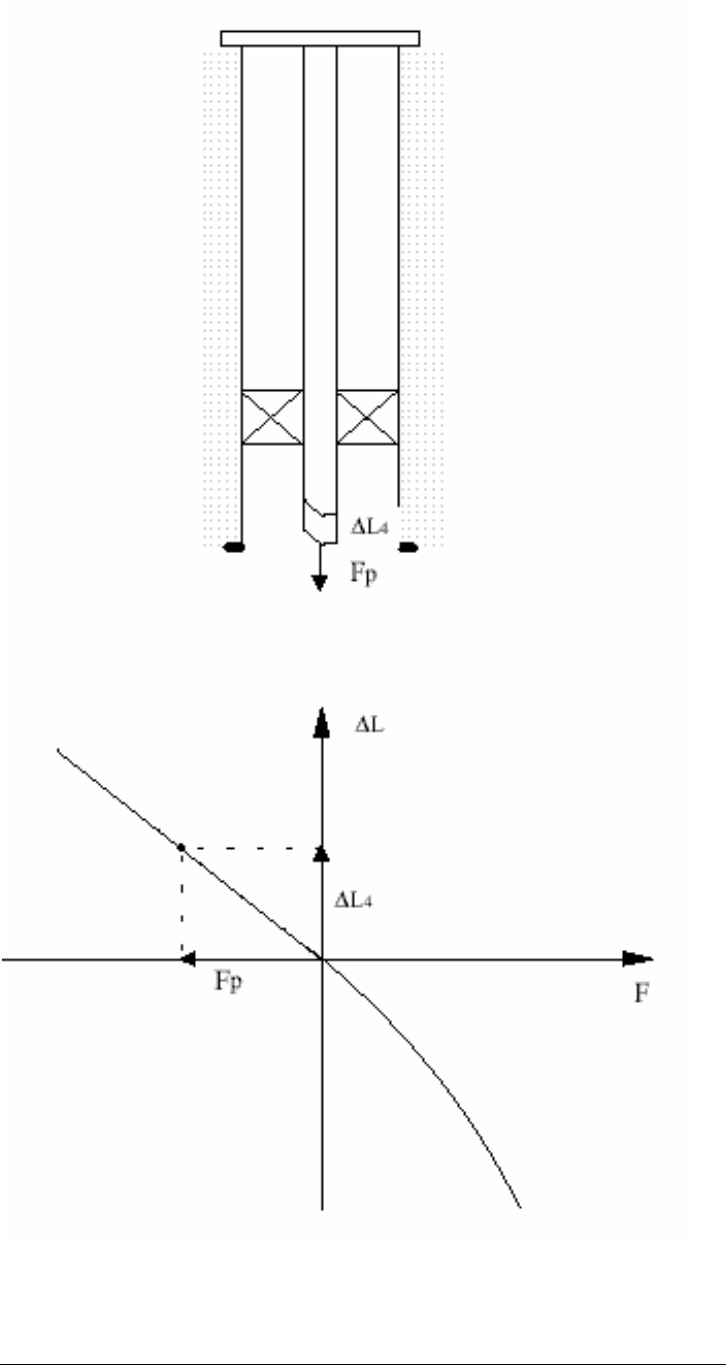
The first step is to plot the characteristic strength/length variation of the system.

This curve, shown in Figure 13-14 is determined by the size of tubing, on the

material, radial distance between the tubing OD and casing ID and on the fluids

in the well. This can be plotted using the following formulae:

L −=Λ

for F < 0 (13-19)

Elw

−−=Λ for F > 0

The second step is to identify on the curve the tubing representative point in the

well when it is subjected to the fictitious force, even when this is negative. On the

curve given in Figure 13-15 this condition is identified by intersection point (Ff,

∆Lf). Indeed, if a force of Ff was applied at the end of the tubing, the cause of the

buckling would be eliminated and the neutral point would return to the bottom in

the tubing.

The origin of the axis moves to the point found in this way (Ff , ∆Lf) and the

diagram obtained has a total length variation of ∆LP = -∆ltot, so to position the

tubing in the packer after contracting the string must be elongated accordingly.

As shown in Figure 13-13 the Fp force, transferred between the tubing and

packer, is then identified.

13-26 Casing/Tubing Design Manual

October 2005

Figure 13-14. Graphical Representation of Movement