Бусыгин В.П., Покатович Е.В., Фридман А.А. Сборник задач по курсу микроэкономики продвинутого уровня (Раздел 1)

Подождите немного. Документ загружается.

Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

(á)

()

1.1.10. Êàêîå ñâîéñòâî ôóíêöèè ïîëåçíîñòè ãàðàíòèðóåò ëîêàëü-

íóþ íåíàñûùàåìîñòü ïðåäñòàâëÿåìûõ åþ ïðåäïî÷òåíèé?

1.1.11*. Èçîáðàçèòå ïðèìåð âûïóêëûõ ëîêàëüíî íåíàñûùàåìûõ

ïðåäïî÷òåíèé, êîòîðûå:

(à) ÿâëÿþòñÿ ñëàáî ìîíîòîííûìè, íî íå ÿâëÿþòñÿ ñòðîãî ìîíî-

òîííûìè;

(á) íå ÿâëÿþòñÿ ñëàáî ìîíîòîííûìè.

1.1.12. Ïðèâåäèòå ïðèìåðû âûïóêëûõ ïðåäïî÷òåíèé, íå ÿâëÿþ-

ùèõñÿ ëîêàëüíî íåíàñûùàåìûìè, êîãäà ó ïîòðåáèòåëÿ â ðàññìàòðè-

âàåìîì ìíîæåñòâå X àëüòåðíàòèâ (ïîòðåáèòåëüñêèõ íàáîðîâ) ñóùå-

ñòâóåò (íå ñóùåñòâóåò) íàèëó÷øåé àëüòåðíàòèâû.

1.1.13. Ïîêàæèòå, ÷òî ñòðîãî âûïóêëûå ïðåäïî÷òåíèÿ ïîòðåáè-

òåëÿ ëîêàëüíî íåíàñûùàåìû òîãäà è òîëüêî òîãäà, êîãäà ó ïîòðåáèòå-

ëÿ â ðàññìàòðèâàåìîì ìíîæåñòâå X àëüòåðíàòèâ (ïîòðåáèòåëüñêèõ

íàáîðîâ) íåò íàèáîëåå ïðåäïî÷èòàåìîé àëüòåðíàòèâû. Íà îñíîâå ýòîãî

óòâåðæäåíèÿ ïîêàæèòå, ÷òî ñòðîãî âûïóêëûå ñëàáî ìîíîòîííûå ïðåä-

ïî÷òåíèÿ ëîêàëüíî íåíàñûùàåìû.

1.1.14. Îòíîñèòåëüíî êàæäîé èç íèæåïðèâåäåííûõ ôóíêöèé ñäå-

ëàéòå âûâîä, ÿâëÿþòñÿ ëè ïðåäñòàâëÿåìûå åþ ïðåäïî÷òåíèÿ:

âûïóêëûìè (ñòðîãî âûïóêëûìè);

ëîêàëüíî íåíàñûùàåìûìè;

ìîíîòîííûìè (ñòðîãî ìîíîòîííûìè);

íåïðåðûâíûìè ïðåäïî÷òåíèÿìè?

(à)

( , ..., ) ( ) ... ( ) .

=++

ux x x x

(á)

( , ..., ) max( , ..., ).

ux x x x

(â)

( , ..., ) min( , ..., ).

ux x x x

(ã)

1/ 2 1/ 2

( , ..., ) ( ) ... ( ) .

=++

ux x x x

Çàäà÷è

(ä)

( , ..., ) ... ... .

=+ ++ + +

ux x x x

(å)

12 1 2 2 1

(, ) min(2 , 2 ).

=−−

ux x x x x x

(æ)

100

( , ..., ) 100, 100, 0.

100

, åñëè

åñëè

, åñëè

αα





==α>







∏∏

∏

∏∏

Nii

ux x x

1.1.15. Ïðåäïîëîæèì, ÷òî ïðåäïî÷òåíèÿ

çàäàííûå íà ìíîæå-

ñòâå âñåõ âåêòîðîâ (ïîòðåáèòåëüñêèõ íàáîðîâ) ñ ïîëîæèòåëüíûìè

êîîðäèíàòàìè, ïðåäñòàâèìû ôóíêöèåé Êîááà  Äóãëàñà

( , ..., )

ux x

=γ

∏

0, 0.

α> γ>

(à) ßâëÿþòñÿ ëè äàííûå ïðåäïî÷òåíèÿ ñòðîãî âûïóêëûìè è ìî-

íîòîííûìè?

(á) Êàê èçìåíèòñÿ âàø îòâåò íà ïóíêò (à), åñëè â êà÷åñòâå äîïó-

ñòèìîãî ìíîæåñòâà ðàññìàòðèâàòü âñå ïîòðåáèòåëüñêèå íàáîðû ñ

íåîòðèöàòåëüíûìè êîýôôèöèåíòàìè?

1.1.16. Ðàññìîòðèòå îòíîøåíèå ïðåäïî÷òåíèÿ

äëÿ êîòîðîãî

ñóùåñòâóåò ïðåäñòàâëÿþùàÿ åãî ôóíêöèÿ ïîëåçíîñòè.

(à) Ïîêàæèòå, ÷òî îòíîøåíèå ïðåäïî÷òåíèÿ

ãîìîòåòè÷íî, åñëè

ôóíêöèÿ ïîëåçíîñòè ïîëîæèòåëüíî îäíîðîäíà.

(á) Ïîêàæèòå, ÷òî âåðíî è îáðàòíîå óòâåðæäåíèå: åñëè îòíîøå-

íèå ïðåäïî÷òåíèÿ

ãîìîòåòè÷íî, òî ñóùåñòâóåò ïîëîæèòåëüíî îä-

íîðîäíàÿ (â ÷àñòíîñòè, ïîëîæèòåëüíî îäíîðîäíàÿ ïåðâîé ñòåïåíè) ôóí-

êöèÿ ïîëåçíîñòè, ïðåäñòàâëÿþùàÿ ýòè ïðåäïî÷òåíèÿ. (Çàìåòèì, ÷òî,

êàê ïîêàçûâàåò ïðèìåð ëåêñèêîãðàôè÷åñêèõ ïðåäïî÷òåíèé, óòâåðæäå-

Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

íèå ïåðåñòàåò áûòü ñïðàâåäëèâûì, åñëè îòêàçàòüñÿ îò ïðåäïîëîæåíèÿ

î ñóùåñòâîâàíèè ïðåäñòàâëÿþùåé ïðåäïî÷òåíèÿ ôóíêöèè ïîëåçíîñòè.)

1.1.17*. Èâàí Èâàíîâè÷ áîëüøå âñåãî ëþáèò ïèâî: ÷åì áîëüøå

ïèâà îí ïîòðåáëÿåò, òåì âûøå óðîâåíü åãî óäîâëåòâîðåííîñòè. Îí

òàêæå ëþáèò ÷èïñû: ïðè êàæäîì äàííîì óðîâíå ïîòðåáëåíèÿ ïèâà,

÷åì áîëüøå ÷èïñîâ ïîòðåáëÿåò Èâàí Èâàíîâè÷, òåì âûøå óðîâåíü

åãî ïîëåçíîñòè. Îäíàêî â ïåðâóþ î÷åðåäü åãî çàáîòèò ïîòðåáëåíèå

ïèâà: ÷åì áîëüøå ïèâà, òåì ëó÷øå (íåçàâèñèìî îò òîãî, ñêîëüêî ÷èï-

ñîâ îí ïðè ýòîì ïîòðåáëÿåò).

(à) Óäîâëåòâîðÿþò ëè ïðåäïî÷òåíèÿ Èâàíà Èâàíîâè÷à àêñèîìàì:

ïîëíîòû;

òðàíçèòèâíîñòè;

ëîêàëüíîé íåíàñûùàåìîñòè;

ñòðîãîé ìîíîòîííîñòè;

ñòðîãîé âûïóêëîñòè;

íåïðåðûâíîñòè?

(á) Ïî÷åìó íåâîçìîæíî ïðåäñòàâèòü ïðåäïî÷òåíèÿ Èâàíà Èâà-

íîâè÷à ñ ïîìîùüþ ôóíêöèè ïîëåçíîñòè?

1.2

Çàäà÷à ìàêñèìèçàöèè ïîëåçíîñòè

è çàäà÷à ìèíèìèçàöèè ðàñõîäîâ

1.2.1. Ðàññìîòðèòå ïîòðåáèòåëÿ, êîòîðûé âûáèðàåò íàèëó÷øèé

ïîòðåáèòåëüñêèé íàáîð â ïðîñòðàíñòâå äâóõ òîâàðîâ. Íàéäèòå ôóíêöèè

ìàðøàëëîâñêîãî è êîìïåíñèðîâàííîãî ñïðîñà äëÿ ñëåäóþùèõ ñëó÷àåâ.

(à)* Òîâàðû ÿâëÿþòñÿ àáñîëþòíûìè (ñîâåðøåííûìè) çàìåíè-

òåëÿìè:

12 1 2

(, ) ,, 0.

=α +β α β>

ux x x x

(á)* Òîâàðû ÿâëÿþòñÿ àáñîëþòíî âçàèìîäîïîëíÿþùèìè:

() min , 0.



=α>





Çàäà÷è

(â) Ïðåäïî÷òåíèÿ êâàçèëèíåéíû è ïðåäñòàâèìû ôóíêöèåé ïîëåç-

íîñòè

12 1 2

(, ) () ,

uxxxx

ãäå

α<

1.2.2. Íàéäèòå ôóíêöèè ñïðîñà, êîñâåííóþ ôóíêöèþ ïîëåçíîñòè

è ôóíêöèþ ðàñõîäîâ ïîòðåáèòåëÿ, ïðåäïî÷òåíèÿ êîòîðîãî ïðåäñòàâè-

ìû ôóíêöèåé ïîëåçíîñòè Êîááà  Äóãëàñà:

( , ..., ) ,

∏

ux x x

α>

Ïîêàæèòå, ÷òî ðàñõîäû òàêîãî ïîòðåáèòåëÿ íà êàæäûé òîâàð

ÿâëÿþòñÿ ôèêñèðîâàííîé äîëåé åãî äîõîäà (ò.å. ýòà äîëÿ íå çàâèñèò

îò öåí è äîõîäà).

1.2.3. Íàéäèòå ôóíêöèè ñïðîñà, êîñâåííóþ ôóíêöèþ ïîëåçíîñòè

è ôóíêöèþ ðàñõîäîâ ïîòðåáèòåëÿ, ïðåäïî÷òåíèÿ êîòîðîãî ïðåäñòàâè-

ìû ôóíêöèåé ïîëåçíîñòè âèäà:

(à)

111

( , ..., ) max( , ..., ),

NNN

ux x x x

=α α

0;α>

(á)

111

( , ..., ) min( , ..., ),

NNN

ux x x x

=α α

α>

(â)

111

( , ..., ) min( , ..., ) ... ;

NnnN

ux x x x x x

=+++

(ã)

( , ..., ) ( ) ... ( ) ,

αα

=++

ux x x x

α>

(ä)

( , ..., ) ( ... ) ,

=+ +

ux x x x

α>

(å)

11 1

( , ..., , ) ,

∏

NN i N

ux x x x x

α>

(æ)

( , ..., ) ... ... ;

=+ +− − −

ux x x x

(ç)

111 1

( , ..., ) max( , ..., ) min( , ..., ).

NNNN

ux x x x x x

=α α+

1.2.4*. Íàéäèòå ôóíêöèè ñïðîñà, êîñâåííóþ ôóíêöèþ ïîëåçíîñ-

òè è ôóíêöèþ ðàñõîäîâ ïîòðåáèòåëÿ, ïðåäïî÷òåíèÿ êîòîðîãî ïðåäñòà-

âèìû ôóíêöèåé ïîëåçíîñòè ñ ïîñòîÿííîé ýëàñòè÷íîñòüþ çàìåùåíèÿ.

1.2.5. Íàéäèòå ôóíêöèè ñïðîñà, êîñâåííóþ ôóíêöèþ ïîëåçíîñòè

è ôóíêöèþ çàòðàò ïîòðåáèòåëÿ, ïðåäïî÷òåíèÿ êîòîðîãî ïðåäñòàâèìû

Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

ôóíêöèåé ïîëåçíîñòè Ñòîóíà:

( , ..., ) ( ) ,

=−γ

∏

Nii

ux x x

γ≥

α>

1.2.6*. Ïîêàæèòå, ÷òî, åñëè ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ ëîêàëüíî

íåíàñûùàåìû, òî áþäæåòíîå îãðàíè÷åíèå âûïîëíÿåòñÿ êàê ðàâåíñòâî.

1.2.7. Ïîêàæèòå, ÷òî åñëè ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ ëîêàëüíî

íåíàñûùàåìû, è ñîîòíîøåíèå

≥ω

âûïîëíÿåòñÿ äëÿ âñåõ x, òàêèõ,

÷òî

òî

≥ω

Áóäåò ëè â ýòîì ñëó÷àå âûïîëíÿòüñÿ ñîîòíîøåíèå

px px

≥

1.2.8*. Ðàññìîòðèòå ïîòðåáèòåëÿ, ôóíêöèÿ ïîëåçíîñòè êîòîðîãî

çàâèñèò îò ïîòðåáëåíèÿ äâóõ òîâàðîâ:

Èçîáðàçèòå ëèíèè óðîâ-

íÿ êîñâåííîé ôóíêöèè ïîëåçíîñòè â ïðîñòðàíñòâå öåí.

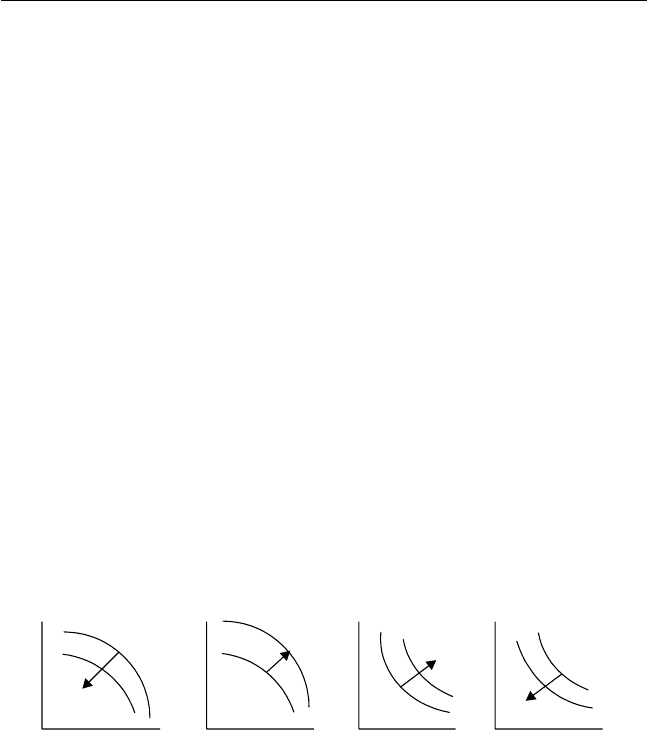
1.2.9*. Ïóñòü ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ ëîêàëüíî íåíàñûùàå-

ìû è ïðåäñòàâèìû íåïðåðûâíîé ôóíêöèåé ïîëåçíîñòè. Îòíîñèòåëüíî

êàæäîãî èç ïðèâåäåííûõ íà ðèñ. 1.1 ãðàôèêîâ (íà ãðàôèêàõ ñòðåëêîé

óêàçàíî íàïðàâëåíèå âîçðàñòàíèÿ ðàñõîäîâ) ñäåëàéòå çàêëþ÷åíèå, ìî-

æåò ëè îí ïðåäñòàâëÿòü ëèíèè óðîâíÿ ôóíêöèè ðàñõîäîâ äëÿ äàííîãî

ïîòðåáèòåëÿ â ïðîñòðàíñòâå öåí?

Ðèñ. 1.1

1.2.10. Ïðè êàêîì óðîâíå äîõîäà è êàêèõ óñëîâèÿõ çíà÷åíèå ìàð-

øàëëîâñêîãî ñïðîñà

(, )xp I

ñîâïàäàåò ñ çàäàííûì çíà÷åíèåì õèê-

ñîâñêîãî ñïðîñà

(, )?hp u

ÀÁÂÃ

Çàäà÷è

1.2.11. Ïðè êàêîì óðîâíå ïîëåçíîñòè è êàêèõ óñëîâèÿõ çíà÷åíèå

õèêñîâñêîãî ñïðîñà

(, )hp u

ñîâïàäàåò ñ çàäàííûì çíà÷åíèåì ìàð-

øàëëîâñêîãî ñïðîñà

(, )?xp I

1.2.12. Ïðè êàêîì óðîâíå äîõîäà è êàêèõ óñëîâèÿõ çíà÷åíèå êîñ-

âåííîé ôóíêöèè ïîëåçíîñòè ðàâíî çàäàííîé âåëè÷èíå ïîëåçíîñòè

1.2.13. Ïðè êàêîì óðîâíå ïîëåçíîñòè u è êàêèõ óñëîâèÿõ çíà÷å-

íèå ôóíêöèè ðàñõîäîâ ðàâíî çàäàííîé âåëè÷èíå äîõîäà

1.2.14. Ïîñòðîéòå àíàëèòè÷åñêèå ïðèìåðû è èçîáðàçèòå ãðàôè-

÷åñêè ñèòóàöèè, êîãäà ðåøåíèå çàäà÷è ìàêñèìèçàöèè ïîëåçíîñòè

(, )xp I

íå ñîâïàäàåò ñ ðåøåíèåì çàäà÷è ìèíèìèçàöèè ðàñõîäîâ

(, ),hp u

ïðåäïîëàãàÿ, ÷òî â çàäà÷å ìèíèìèçàöèè ðàñõîäîâ óðîâåíü

ïîëåçíîñòè â îãðàíè÷åíèè ðàâåí

()

(, )uxpI

(ò.å. ñîâïàäàåò ñ ìàêñè-

ìàëüíîé ïîëåçíîñòüþ, ïîëó÷àåìîé ïðè ðåøåíèè ïåðâîé çàäà÷è). (Â ïðè-

ìåðàõ äîëæíû áûòü ñïåöèôèöèðîâàíû ôóíêöèè è ïðèâåäåíû çíà÷åíèÿ

ýêçîãåííûõ ïàðàìåòðîâ.)

1.2.15. Äîêàæèòå òîæäåñòâî Ðîÿ è ëåììó Øåïàðäà íà îñíîâå

òåîðåìû îá îãèáàþùåé.

1.2.16. Ïîêàæèòå, ÷òî åñëè ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ ãîìîòå-

òè÷íû, òî ôóíêöèè ñïðîñà óäîâëåòâîðÿþò ñîîòíîøåíèþ

(, )

∂

xpI

(, )

∂

xpI

äëÿ âñåõ i è j.

1.2.17. Ïðåäïîëîæèì, ÷òî ñòðîãî âûïóêëûå, ñòðîãî ìîíîòîííûå

ïðåäïî÷òåíèÿ ïðåäñòàâëÿþòñÿ äèôôåðåíöèðóåìîé ôóíêöèåé ïîëåçíî-

ñòè. Âåðíî ëè óòâåðæäåíèå: «Ïðåäåëüíàÿ ïîëåçíîñòü äîõîäà

(, )vp I

∂

ïîëîæèòåëüíà äëÿ ëþáûõ öåí è äîõîäîâ»? Àðãóìåíòèðóéòå ñâîé îòâåò.

1.2.18. Ïðåäïîëîæèì, ÷òî äëÿ ôóíêöèè ïîëåçíîñòè u(x) êîñâåí-

íàÿ ôóíêöèÿ ïîëåçíîñòè èìååò ôîðìó Ãîðìàíà:

(, ) () ().vp I ap bpI

Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

Êàê âû÷èñëèòü çíà÷åíèå ôóíêöèè ðàñõîäîâ ýòîãî ïîòðåáèòåëÿ äëÿ öåí

p è ïîëåçíîñòè u, åñëè èçâåñòíû çíà÷åíèÿ âåëè÷èí

()ap

()?bp

1.2.19. Îõàðàêòåðèçóåòå âçàèìîñâÿçü ìåæäó êîñâåííîé ôóíêöè-

åé ïîëåçíîñòè è ôóíêöèåé ðàñõîäîâ, âû÷èñëåííûìè äëÿ ôóíêöèè ïî-

ëåçíîñòè, ïðåäñòàâëÿþùåé äàííûå ïðåäïî÷òåíèÿ.

1.2.20. Ïîêàæèòå, ÷òî åñëè ôóíêöèÿ ìàðøàëëîâñêîãî ñïðî-

ñà

(, )xp I

ïîðîæäåíà ëîêàëüíî íåíàñûùàåìûìè ïðåäïî÷òåíèÿìè, òî

âûïîëíÿåòñÿ ñëåäóþùåå ñîîòíîøåíèå:

αε =

∑

ãäå

 äîëÿ ðàñ-

õîäîâ íà áëàãî i,

 ýëàñòè÷íîñòü ñïðîñà íà áëàãî i ïî äîõîäó.

1.2.21. Ïîêàæèòå, ÷òî åñëè ôóíêöèÿ ìàðøàëëîâñêîãî ñïðîñà

(, )xp I

ÿâëÿåòñÿ ïîëîæèòåëüíî îäíîðîäíîé íóëåâîé ñòåïåíè, òî âû-

ïîëíÿåòñÿ ñëåäóþùåå ñîîòíîøåíèå:

=−ε

∑

ãäå

 ýëàñòè÷-

íîñòü ñïðîñà íà áëàãî k ïî öåíå áëàãà i,

 ýëàñòè÷íîñòü ñïðîñà íà

áëàãî k ïî äîõîäó.

1.2.22. Ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ îïèñûâàþòñÿ ñëåäóþùåé

ôóíêöèåé ïîëåçíîñòè:

111 1

( , ..., , ) ( , ..., ) .

nn n n

ux x x vx x x

Ïîêàæèòå,

÷òî ïðè äîñòàòî÷íî áîëüøîì äîõîäå (ïîòðåáèòåëü ïðè ýòîì äîõîäå

ïðåäúÿâëÿåò ïîëîæèòåëüíûé ñïðîñ íà áëàãî

(à) êîñâåííàÿ ôóíêöèÿ ïîëåçíîñòè èìååò âèä

(, ) () ;vp I ap I

(á) ôóíêöèÿ

()ap

ÿâëÿåòñÿ âûïóêëîé.

1.2.23. Ïóñòü ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ ïðåäñòàâèìû ôóíêöè-

åé

() ( , , ) ,

ux x x x

−

=φ +

ïðè÷åì

 âîçðàñòàþùàÿ è âîãíóòàÿ.

(à) Ïóñòü íàáîð

( , , , ) 0

xx x x

−

=>>

%% % %

 îïòèìàëüíûé íàáîð

äëÿ äàííîãî ïîòðåáèòåëÿ ïðè âåêòîðå öåí p è äîõîäå I. Êàê èçìåíèòñÿ

îïòèìàëüíûé âûáîð ïîòðåáèòåëÿ, åñëè åãî äîõîä âîçðàñòåò íà 10%?

(á) Ïóñòü íàáîð

( , , , ) 0

xx x x

−

=>>

%% % %

ñëóæèò ðåøåíèåì çà-

äà÷è ìèíèìèçàöèè ðàñõîäîâ äëÿ äàííîãî ïîòðåáèòåëÿ ïðè âåêòîðå öåí

Çàäà÷è

p è óðîâíå ïîëåçíîñòè

Êàê èçìåíèòñÿ ðåøåíèå ýòîé çàäà÷è, åñëè

âîçðàñòåò íà 10%?

1.2.24. Ìàòðèöà

á7 â

ã2ä

å1





=−



ϕ−



ÿâëÿåòñÿ ìàòðèöåé çàìåùå-

íèÿ Ñëóöêîãî, ïîäñ÷èòàííîé ïðè öåíàõ

1, 2

Íàéäè-

òå çíà÷åíèÿ ïàðàìåòðîâ

, , , , , .

αβγδεϕ

1.2.25. Ìîãóò ëè âñå áëàãà áûòü èíôåðèîðíûìè, åñëè ïðåäïî÷-

òåíèÿ ëîêàëüíî íåíàñûùàåìû? Àðãóìåíòèðóéòå ñâîé îòâåò.

1.2.26. Ïîêàæèòå, ÷òî åñëè ôóíêöèÿ ïîëåçíîñòè ïîòðåáèòåëÿ ñå-

ïàðàáåëüíà, òî íè îäíî èç áëàã íå ìîæåò áûòü òîâàðîì Ãèôôåíà. Àð-

ãóìåíòèðóéòå ñâîé îòâåò.

1.2.27. Ðàññìîòðèòå ïîòðåáèòåëÿ, ïðåäïî÷òåíèÿ êîòîðîãî ëîêàëü-

íî íåíàñûùàåìû è ïðåäñòàâèìû àääèòèâíî ñåïàðàáåëüíîé äâàæäû

äèôôåðåíöèðóåìîé ôóíêöèåé ïîëåçíîñòè:

() ( ),

Ux u x

∑

ïðè-

÷åì

()

⋅

ñòðîãî âîãíóòû äëÿ ëþáîãî i. Ïóñòü ïîòðåáèòåëü îáëàäàåò

äîõîäîì

0,I >

à öåíû òîâàðîâ çàäàíû âåêòîðîì

0.p

Èçâåñòíî,

÷òî

(, ) 0.xp I

Ïîêàæèòå, ÷òî ïðåäåëüíàÿ ïîëåçíîñòü äîõîäà â òî÷êå

(, )xp I

óáûâàåò ïî äîõîäó.

1.2.28. Ïðåäïîëîæèì, ÷òî äîõîä ïîòðåáèòåëÿ ôîðìèðóåòñÿ ýí-

äîãåííî è ïðåäñòàâëÿåò ñîáîé ðûíî÷íóþ ñòîèìîñòü åãî ïåðâîíà÷àëü-

íîãî çàïàñà. Êàê èçìåíèòñÿ ïðè ýòîì òîæäåñòâî Ñëóöêîãî?

1.2.29*. Ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ îïèñûâàþòñÿ ôóíêöèåé ïî-

ëåçíîñòè

(, ).

ux x

Ïîòðåáèòåëü íå èìååò äåíåã, íî îáëàäàåò ïåðâî-

íà÷àëüíûìè çàïàñàìè òîâàðîâ: ó íåãî åñòü

åäèíèö ïåðâîãî òîâàðà

åäèíèö âòîðîãî òîâàðà.

(a) Âîçìîæíà ëè òàêàÿ ñèòóàöèÿ, ïðè êîòîðîé ïîâûøåíèå öåíû

îäíîãî èç òîâàðîâ óâåëè÷èëî áû ïîëåçíîñòü ýòîãî ïîòðåáèòåëÿ?

Îáúÿñíèòå.

Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

(á) Ïóñòü öåíà ïåðâîãî òîâàðà âîçðîñëà. Êàê èçìåíèòñÿ ïîòðåá-

ëåíèå ýòîãî òîâàðà? Ïðîêîììåíòèðóéòå çíàêè ýôôåêòà çàìåùåíèÿ è

ýôôåêòà äîõîäà.

1.3

Äâîéñòâåííîñòü â òåîðèè ïîòðåáèòåëÿ.

Ïðîáëåìà âîññòàíîâëåíèÿ ïðåäïî÷òåíèé

1.3.1*. Ôóíêöèÿ ðàñõîäîâ èìååò âèä

(, , )2 .

xy xy

ep p u u pp

Íàéäèòå ôóíêöèþ ïîëåçíîñòè. (Ïîäñêàçêà: èñïîëüçóéòå ëåììó Øå-

ïàðäà.)

1.3.2. Ïðè êàêèõ ïàðàìåòðàõ à è b ôóíêöèÿ

(, )

e p u aup p

áó-

äåò ôóíêöèåé ðàñõîäîâ íåêîòîðîãî ïîòðåáèòåëÿ? Íàéäèòå ôóíêöèþ

ïîëåçíîñòè ýòîãî ïîòðåáèòåëÿ.

1.3.3. Ïðè êàêèõ ïàðàìåòðàõ ôóíêöèÿ

(, ) ()

∏

ep u au p

ÿâ-

ëÿåòñÿ ôóíêöèåé ðàñõîäîâ ïîòðåáèòåëÿ? Íàéäèòå ôóíêöèþ ïîëåçíîñ-

òè, ñîîòâåòñòâóþùóþ äàííîé ôóíêöèè ðàñõîäîâ.

1.3.4. ßâëÿåòñÿ ëè ôóíêöèÿ

(, , ) ,

xy xy

vp p I Ip p

−α α−

ãäå

01,

<α<

êîñâåííîé ôóíêöèåé ïîëåçíîñòè? Âîññòàíîâèòå ôóíêöèþ ïîëåçíîñòè

(, ).ux y

1.3.5. Ïðåäïîëîæèì, ÷òî ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ ïðåäñòàâ-

ëÿþòñÿ ôóíêöèåé ïîëåçíîñòè

().ux

Ïîêàæèòå, ÷òî ôóíêöèÿ ïîëåçíîñ-

òè ëèíåéíà

()

ux ax







∑

òîãäà è òîëüêî òîãäà, êîãäà êîñâåííàÿ ôóíê-

öèÿ ïîëåçíîñòè èìååò âèä

(, ) .

min( / )

iii

vp I

Çàäà÷è

1.3.6*. Ïóñòü ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ îïèñûâàþòñÿ ñëåäóþ-

ùåé ôóíêöèåé ïîëåçíîñòè:

() ln , 0.

=α α>

∑

iii

ux x

(à) Ñ÷èòàÿ âñå öåíû ïîëîæèòåëüíûìè, íàéäèòå ôóíêöèþ ðàñõî-

äîâ è âîññòàíîâèòå íà åå îñíîâå ôóíêöèþ ïîëåçíîñòè. Ñîâïàäàåò ëè

âîññòàíîâëåííàÿ ôóíêöèÿ ñ ïåðâîíà÷àëüíîé?

(á) Ïîâòîðèòå âñå øàãè ïóíêòà (à) äëÿ äðóãîãî ïîòðåáèòåëÿ,

ôóíêöèÿ ïîëåçíîñòè êîòîðîãî èìååò âèä

()

() min ln , 0.

=α α>

ii i

ux x

(â) Îáñóäèòå ïðîöåäóðó âîññòàíîâëåíèÿ ïðåäïî÷òåíèé íà îñíî-

âå êîñâåííîé ôóíêöèè ïîëåçíîñòè (íå ïåðåõîäÿ îò íåå ê ôóíêöèè ðàñ-

õîäîâ). Ïðîäåìîíñòðèðóéòå, êàê ðàáîòàåò ýòà ñõåìà íà ïðèìåðå ïóíê-

òà (à).

1.3.7. Ïðåäïîëîæèì, ÷òî ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ ïðåäñòàâ-

ëÿþòñÿ ôóíêöèåé ïîëåçíîñòè

().ux

Ïîêàæèòå, ÷òî áëàãà êîìïëåìåí-

òàðíû

() min







òîãäà è òîëüêî òîãäà, êîãäà êîñâåííàÿ ôóíê-

öèÿ ïîëåçíîñòè èìååò âèä

(, ) .

vp I ap I







∑

1.3.8. Íà ðèñ. 1.2 èçîáðàæåíà òèïè÷íàÿ ëèíèÿ óðîâíÿ êîñâåííîé

ôóíêöèè ïîëåçíîñòè â ïðîñòðàíñòâå öåí, ò.å.

{}

12 12

(, ) :(, , ) .

pp R vppI u

∈=

(à) Èçîáðàçèòå íà ðèñóíêå, êàêèå öåíû ñîîòâåòñòâóþò áîëåå

âûñîêîìó óðîâíþ ïîëåçíîñòè, ÷åì

(á) Äëÿ äàííîãî óðîâíÿ ïîëåçíîñòè ôóíêöèÿ ðàñõîäîâ òàêæå ÿâ-

ëÿåòñÿ ôóíêöèåé öåí. Èçîáðàçèòå êðèâóþ ïîñòîÿííûõ ðàñõîäîâ, ò.å.

ìíîæåñòâî

{}

12 12

(, ) :(, , ) .

pp R eppu I

∈=

(â) ×åìó ðàâåí íàêëîí ëèíèè óðîâíÿ ôóíêöèè v â òî÷êå

(, )?

∗∗