Бусыгин В.П., Покатович Е.В., Фридман А.А. Сборник задач по курсу микроэкономики продвинутого уровня (Раздел 1)

Подождите немного. Документ загружается.

Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

• Ñóùåñòâîâàíèå ôóíêöèè ïîëåçíîñòè.

Ïóñòü ïðåäïî÷òåíèÿ

îïðåäåëåííûå íà ìíîæåñòâå X, ðàöèîíàëü-

íû è óäîâëåòâîðÿþò àêñèîìå íåïðåðûâíîñòè. Òîãäà ñóùåñòâóåò íåïðå-

ðûâíàÿ ôóíêöèÿ ïîëåçíîñòè u(x), ïðåäñòàâëÿþùàÿ ýòè ïðåäïî÷òåíèÿ.

Çàäà÷à ìàêñèìèçàöèè ïîëåçíîñòè

Ïóñòü ïðåäïî÷òåíèÿ ïîòðåáèòåëåé ïðåäñòàâèìû ñ ïîìîùüþ

íåïðåðûâíîé ôóíêöèè ïîëåçíîñòè u(x). Îáîçíà÷èì âåêòîð öåí ÷åðåç

( , , ..., ).

ppp p

Áþäæåòíîå ìíîæåñòâî ïîòðåáèòåëÿ ìîæíî çàïè-

ñàòü êàê

{: },

=∈ ≤

BxXpxI

ãäå I  äîõîä ïîòðåáèòåëÿ.

Òîãäà çàäà÷à ïîòðåáèòåëÿ, êîòîðàÿ çàêëþ÷àåòñÿ â âûáîðå íàè-

áîëåå ïðåäïî÷òèòåëüíîãî íàáîðà ïðè äàííûõ öåíàõ è óðîâíå äîõîäà,

èìååò ñëåäóþùèé âèä:

max ( )

≥

≤

px I

Ðåøàÿ çàäà÷ó ìàêñèìèçàöèè ïîëåçíîñòè íà áþäæåòíîì ìíîæå-

ñòâå, ïîëó÷àåì, ÷òî êàæäîé ïàðå (p, I) ñîîòâåòñòâóåò ìíîæåñòâî íàè-

ëó÷øèõ ïðè äàííûõ öåíàõ è äîõîäå ïîòðåáèòåëüñêèõ íàáîðîâ x(p, I),

êîòîðîå áóäåì íàçûâàòü âàëüðàñîâñêèì èëè ìàðøàëëîâñêèì ñïðî-

ñîì ëèáî ïðîñòî ñïðîñîì. Â îáùåì ñëó÷àå x(p, I) íå ÿâëÿåòñÿ îäíî-

çíà÷íûì ñîîòâåòñòâèåì. Åñëè æå êàæäîé ïàðå (p, I) ñîîòâåòñòâóåò

åäèíñòâåííûé íàèëó÷øèé ïîòðåáèòåëüñêèé íàáîð, òî x(p, I) íàçûâà-

þò ôóíêöèåé ìàðøàëëîâñêîãî ñïðîñà. Èç çàäà÷è ïîòðåáèòåëÿ, ïî-

ìèìî õàðàêòåðèñòèêè ñïðîñà, ïîëó÷àåì çàâèñèìîñòü ïîëåçíîñòè îò

ýêçîãåííûõ ïàðàìåòðîâ, òàêèõ, êàê öåíû è äîõîä, åñëè ïîäñòàâèòü íàé-

äåííûé ñïðîñ â öåëåâóþ ôóíêöèþ. Ïîëó÷åííóþ ôóíêöèþ íàçûâàþò

êîñâåííîé ôóíêöèåé ïîëåçíîñòè: v(p, I) = u(

) ãäå

∈ x(p, I).

• Ñâîéñòâà ìàðøàëëîâñêîãî ñïðîñà.

Ïóñòü u(

)  íåïðåðûâíàÿ ôóíêöèÿ, ïðåäñòàâëÿþùàÿ ïðåäïî÷-

òåíèÿ ïîòðåáèòåëÿ, îïðåäåëåííûå íà ìíîæåñòâå

òîã-

äà x(p, I) óäîâëåòâîðÿåò ñëåäóþùèì ñâîéñòâàì:

Îñíîâíûå îïðåäåëåíèÿ è óòâåðæäåíèÿ

1) îäíîðîäíîñòü íóëåâîé ñòåïåíè îòíîñèòåëüíî öåí è äîõîäà:

()

,(, )

λλ=

pI xpI

äëÿ ëþáîãî

λ>

2) åñëè ïðåäïî÷òåíèÿ ëîêàëüíî íåíàñûùàåìûå, òî ìàðøàëëîâ-

ñêèé ñïðîñ óäîâëåòâîðÿåò áþäæåòíîìó îãðàíè÷åíèþ â ôîðìå ðàâåí-

ñòâà: äëÿ ëþáîãî x ∈ x(p, I) èìååì px = I;

3) åñëè ïðåäïî÷òåíèÿ âûïóêëû, òî x(p, I)  âûïóêëîå ìíîæåñòâî;

4) åñëè ïðåäïî÷òåíèÿ ñòðîãî âûïóêëû (ñëåäîâàòåëüíî, u(

) ñòðî-

ãî êâàçèâîãíóòàÿ), òî äëÿ êàæäîé ïàðû (p, I) ìíîæåñòâî x(p, I) ñîñòî-

èò èç îäíîãî ýëåìåíòà, ò.å. x(p, I) ÿâëÿåòñÿ ôóíêöèåé ñïðîñà è, êðîìå

òîãî, x(p, I)  íåïðåðûâíàÿ ôóíêöèÿ.

• Ñâîéñòâà êîñâåííîé ôóíêöèåé ïîëåçíîñòè.

Ïóñòü u(

)  íåïðåðûâíàÿ ôóíêöèÿ, ïðåäñòàâëÿþùàÿ ïðåäïî÷-

òåíèÿ ïîòðåáèòåëÿ, îïðåäåëåííûå íà ìíîæåñòâå

Òîã-

äà v(p, I) óäîâëåòâîðÿåò ñëåäóþùèì ñâîéñòâàì:

1) îäíîðîäíîñòü íóëåâîé ñòåïåíè îòíîñèòåëüíî (p, I) : v(λp, λI) =

= v(p, I) äëÿ ëþáîãî λ > 0;

2) íå óáûâàåò ïî äîõîäó; ñòðîãî âîçðàñòàåò ïî äîõîäó, åñëè ïðåä-

ïî÷òåíèÿ ëîêàëüíî íåíàñûùàåìû;

3) íå âîçðàñòàåò ïî öåíàì;

4) êâàçèâûïóêëà ïî p è I, ò.å. ìíîæåñòâî

{}

(,):(,)

≤

pI vpI v

âû-

ïóêëî ïðè ëþáîì

5) íåïðåðûâíà ïî p è I;

6) åñëè ïðåäïî÷òåíèÿ ëîêàëüíî íåíàñûùàåìû è ñòðîãî âûïóêëû

(u(

) ñòðîãî êâàçèâîãíóòà) è ôóíêöèÿ v(p, I) äèôôåðåíöèðóåìà

ïðè

(,) 0,

òî âûïîëíÿåòñÿ òîæäåñòâî Ðîÿ

(,)

(,) .

(,)

∂

=−

∂

vpI

xpI

vpI

Çàäà÷à ìèíèìèçàöèè ðàñõîäîâ

Ïóñòü {:()}

=∈ ≥

VxXuxu

 ìíîæåñòâî òàêèõ íàáîðîâ èç ïî-

òðåáèòåëüñêîãî ìíîæåñòâà X, ïîëåçíîñòü êîòîðûõ íå ìåíüøå çàäàí-

íîãî óðîâíÿ

Òîãäà çàäà÷à ìèíèìèçàöèè ðàñõîäîâ ïðèìåò âèä

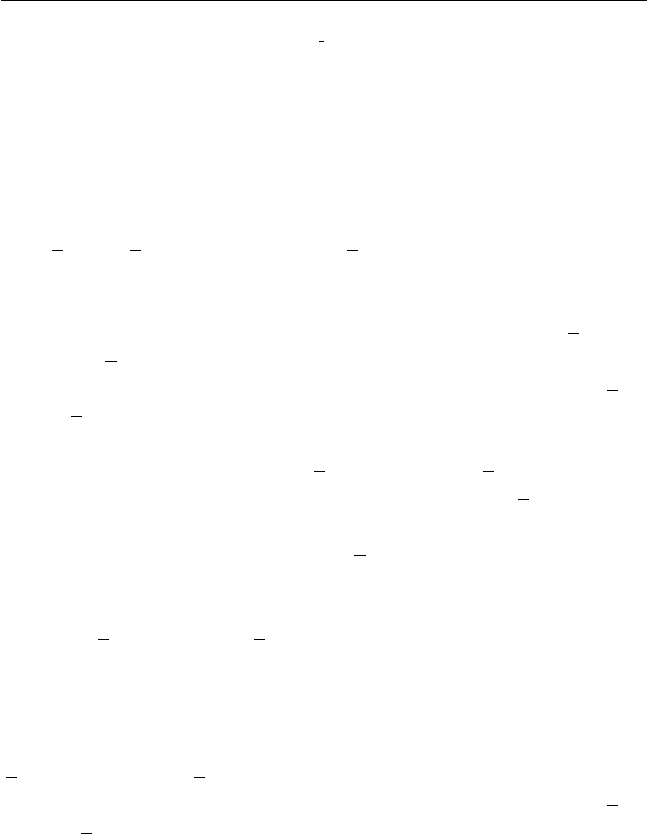
Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

min .

∈

Ðåøåíèÿ ýòîé çàäà÷è (ïðè ðàçëè÷íûõ çíà÷åíèÿõ öåí è ïîëåçíîñ-

òè) îáîçíà÷èì ÷åðåç h(p, u), è áóäåì íàçûâàòü ñîîòâåòñòâóþùåå îòî-

áðàæåíèå êîìïåíñèðîâàííûì ñïðîñîì èëè ñïðîñîì ïî Õèêñó. Ïîä-

ñòàâèâ ðåøåíèå çàäà÷è â öåëåâóþ ôóíêöèþ, ïîëó÷àåì çàâèñèìîñòü

óðîâíÿ ìèíèìàëüíûõ ðàñõîäîâ îò öåí è óðîâíÿ ïîëåçíîñòè. Ïîëó÷åí-

íóþ ôóíêöèþ, îòðàæàþùóþ ýòó çàâèñèìîñòü, íàçûâàþò ôóíêöèåé

ðàñõîäîâ. Â äàëüíåéøåì áóäåì îáîçíà÷àòü ýòó ôóíêöèþ ÷åðåç

(, ):(, ) ,

ep u ep u px

ãäå

(, ).

∈

xhpu

• Ñâîéñòâà êîìïåíñèðîâàííîãî ñïðîñà.

Ïóñòü u(

)  íåïðåðûâíàÿ ôóíêöèÿ, ïðåäñòàâëÿþùàÿ ïðåäïî÷òå-

íèÿ ïîòðåáèòåëÿ, îïðåäåëåííûå íà ìíîæåñòâå

p (0).

≥

Òîãäà

(, )hp u

óäîâëåòâîðÿåò ñëåäóþùèì ñâîéñòâàì:

1) îäíîðîäíîñòü íóëåâîé ñòåïåíè îòíîñèòåëüíî öåí:

(, )hpu

λ=

(, )

hp u

äëÿ ëþáîãî λ > 0;

2) îãðàíè÷åíèå çàäà÷è ìèíèìèçàöèè ðàñõîäîâ âûïîëíÿåòñÿ êàê

ðàâåíñòâî: äëÿ ëþáîãî

(, )

∈

xhpu

èìååì

() ;

ux u

3) åñëè ïðåäïî÷òåíèÿ âûïóêëû, òî ìíîæåñòâî

(, )hp u

âûïóêëî;

4) åñëè ïðåäïî÷òåíèÿ ñòðîãî âûïóêëû (ñëåäîâàòåëüíî, u(

) ñòðî-

ãî êâàçèâîãíóòà), òî ìíîæåñòâî

(, )hp u

ñîñòîèò èç îäíîãî ýëåìåíòà,

ò.å. îòîáðàæåíèå ÿâëÿåòñÿ ôóíêöèåé êîìïåíñèðîâàííîãî ñïðîñà;

5) èìååò ìåñòî çàêîí êîìïåíñèðîâàííîãî ñïðîñà: äëÿ ëþáûõ

(, )

∈′′

xhpu

(, )

∈′′ ′′

xhpu

èìååì

()()

′′ ′′ ′′′ ′′

−− −=

px x p x x

()()0.

′′′′′′

=− −≤

ppxx

• Ñâîéñòâà ôóíêöèè ðàñõîäîâ.

Ïóñòü u(

)  íåïðåðûâíàÿ ôóíêöèÿ, ïðåäñòàâëÿþùàÿ ïðåäïî÷-

òåíèÿ ïîòðåáèòåëÿ, îïðåäåëåííûå íà ìíîæåñòâå

(0).

≥

Òîãäà

(, )ep u

óäîâëåòâîðÿåò ñëåäóþùèì ñâîéñòâàì:

1) îäíîðîäíîñòü ïåðâîé ñòåïåíè îòíîñèòåëüíî öåí:

(, )epu

λ=

(, )ep u

=λ

äëÿ âñåõ

λ>

2) âîçðàñòàåò ïî óðîâíþ ïîëåçíîñòè;

3) íå óáûâàåò ïî öåíàì;

Îñíîâíûå îïðåäåëåíèÿ è óòâåðæäåíèÿ

4) âîãíóòà ïî öåíàì;

5) íåïðåðûâíà;

6) åñëè ïðåäïî÷òåíèÿ ñòðîãî âûïóêëû (u(

) ñòðîãî êâàçèâîãíóòà)

è ôóíêöèÿ

(, )ep u

äèôôåðåíöèðóåìà ïðè

òî âî âíóòðåííèõ òî÷-

êàõ

(0)

èìååò ìåñòî ëåììà Øåïàðäà

(, )

(, ) .

∂

ep u

hpu

Äâîéñòâåííîñòü â òåîðèè ïîòðåáèòåëÿ

• Òåîðåìà äâîéñòâåííîñòè.

1. Ïóñòü u(

)  ôóíêöèÿ ïîëåçíîñòè, ïðåäñòàâëÿþùàÿ ëîêàëüíî

íåíàñûùàåìûå ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ, îïðåäåëåííûå íà ìíîæå-

ñòâå

Åñëè

 ðåøåíèå çàäà÷è ìàêñèìèçàöèè ïîëåçíîñòè

ïðè öåíàõ

è äîõîäå

0,>I

òî

ÿâëÿåòñÿ ðåøåíèåì çàäà÷è

ìèíèìèçàöèè ðàñõîäîâ ïðè

().

uux

Áîëåå òîãî,

(, ) .

ep u I

2. Ïóñòü u(

)  íåïðåðûâíàÿ ôóíêöèÿ ïîëåçíîñòè, ïðåäñòàâëÿþ-

ùàÿ ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ, îïðåäåëåííûå íà ìíîæåñòâå

Åñëè

 ðåøåíèå çàäà÷è ìèíèìèçàöèè ðàñõîäîâ ïðè

(0),

≥

òî

 ðåøåíèå çàäà÷è ìàêñèìèçàöèè ïîëåçíîñòè ïðè öå-

íàõ

è äîõîäå

(, ).

Iepu

Áîëåå òîãî,

(, ) .

vp I u

Ñîîòíîøåíèÿ äâîéñòâåííîñòè äëÿ ëîêàëüíî íåíàñûùàåìûõ

íåïðåðûâíûõ ïðåäïî÷òåíèé:

()

(, ) , (, );

xp I hp vp I

()

(, ) , (, );

hp u xp ep u

()

, ( , ) ;

vpepu u

()

, ( , ) .

epvpI I

• Óðàâíåíèå Ñëóöêîãî.

Ïóñòü u(

)  íåïðåðûâíàÿ ôóíêöèÿ ïîëåçíîñòè, ïðåäñòàâëÿþ-

ùàÿ ñòðîãî âûïóêëûå ëîêàëüíî íåíàñûùàåìûå ïðåäïî÷òåíèÿ ïîòðåáè-

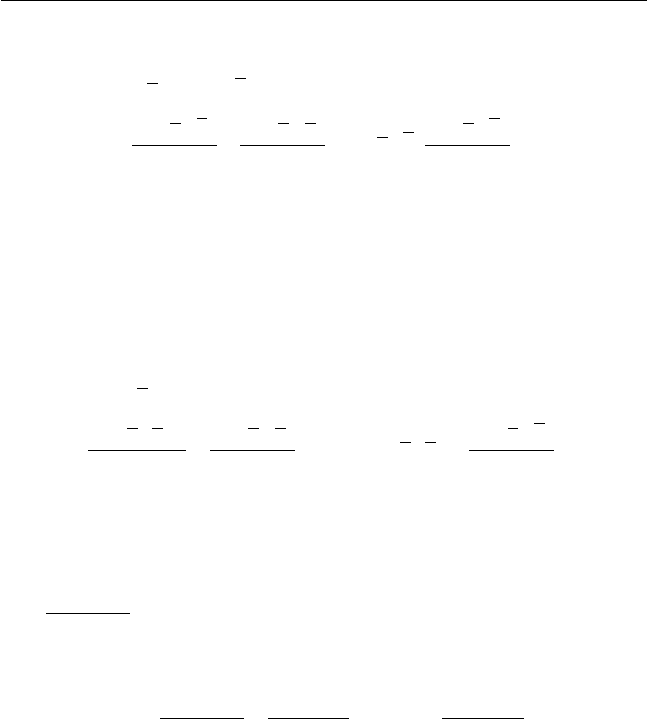
Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

òåëÿ, îïðåäåëåííûå íà ìíîæåñòâå

Åñëè

(, )xp I

(, )hp u



äèôôåðåíöèðóåìûå ôóíêöèè ìàðøàëëîâñêîãî è êîìïåíñèðîâàííîãî ñïðî-

ñà, òî äëÿ âñåõ

èìååò ìåñòî óðàâíåíèå Ñëóöêîãî

( , ) ( , ) ( , )

(, ) .

∂∂ ∂

=−

∂∂ ∂

ii i

xpI hpu xpI

xpI

pp I

• Óðàâíåíèå Ñëóöêîãî äëÿ ñëó÷àÿ íàòóðàëüíîãî äîõîäà.

Ïóñòü u(

)  íåïðåðûâíàÿ ôóíêöèÿ ïîëåçíîñòè, ïðåäñòàâëÿþùàÿ

ñòðîãî âûïóêëûå ëîêàëüíî íåíàñûùàåìûå ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ,

îïðåäåëåííûå íà ìíîæåñòâå

Åñëè

(, )

xp p

 ôóíêöèÿ ñïðî-

ñà ïðè íàëè÷èè íàòóðàëüíîãî äîõîäà,

(, )xp I

 ôóíêöèÿ ìàðøàëëîâ-

ñêîãî ñïðîñà ïðè ôèêñèðîâàííîì äîõîäå è

(, )hp u

 ôóíêöèÿ êîì-

ïåíñèðîâàííîãî ñïðîñà, òî ïðè óñëîâèè äèôôåðåíöèðóåìîñòè ýòèõ ôóí-

êöèé äëÿ âñåõ

èìååò ìåñòî îáîáùåííîå óðàâíåíèå Ñëóöêîãî

()

( , ) ( , ) ( , )

(, ) .

ω∂ ∂

=+ω−ω

∂∂

ii i

dxpp hpu xpI

xpp

dp p I

Ýëåìåíòàìè

ìàòðèöû Ñëóöêîãî èëè ìàòðèöû êîýôôèöè-

åíòîâ çàìåùåíèÿ (îáîçíà÷èì åå ÷åðåç S) ÿâëÿþòñÿ ýôôåêòû çàìå-

ùåíèÿ äëÿ ñïðîñà íà i-é òîâàð ïðè èçìåíåíèè öåíû j-ãî áëàãà, ò.å.

(, )

∂

hpu

Ñ ó÷åòîì óðàâíåíèÿ Ñëóöêîãî êàæäûé ýëåìåíò ìàò-

ðèöû ìîæåò áûòü âûðàæåí ÷åðåç ìàðøàëëîâñêèé ñïðîñ:

(, ) (, ) (, )

(,) .

∂∂ ∂

==+

∂∂ ∂

ii i

ij j

hpu xpI xpI

sxpI

pp I

• Ñâîéñòâà ìàòðèöû çàìåùåíèÿ Ñëóöêîãî.

Ïóñòü u(

)  íåïðåðûâíàÿ ôóíêöèÿ ïîëåçíîñòè, ïðåäñòàâëÿþ-

ùàÿ ñòðîãî âûïóêëûå ëîêàëüíî íåíàñûùàåìûå ïðåäïî÷òåíèÿ ïîòðå-

áèòåëÿ, îïðåäåëåííûå íà ìíîæåñòâå

Ïóñòü ôóíêöèÿ ðàñõî-

äîâ

(, )ep u

äâàæäû íåïðåðûâíî äèôôåðåíöèðóåìàÿ, òîãäà ìàòðèöà

çàìåùåíèÿ Ñëóöêîãî

(, )SpI

óäîâëåòâîðÿåò ñëåäóþùèì óñëîâèÿì:

Îñíîâíûå îïðåäåëåíèÿ è óòâåðæäåíèÿ

(, )SpI

 ñèììåòðè÷íàÿ ìàòðèöà;

(, )SpI

 îòðèöàòåëüíî ïîëóîïðåäåëåííàÿ;

(, ) 0.

SpIp

Çàäà÷à âîññòàíîâëåíèÿ ïðåäïî÷òåíèé

• Ñâÿçü èñõîäíûõ è âîññòàíîâëåííûõ ïðåäïî÷òåíèé.

1. Ïóñòü

(, )ep u

 ôóíêöèÿ ðàñõîäîâ äëÿ ðàöèîíàëüíûõ, íåïðå-

ðûâíûõ ïðåäïî÷òåíèé, îïðåäåëåííûõ íà ìíîæåñòâå

è ïðåä-

ñòàâëåííûõ ìíîæåñòâîì

Åñëè

 ìíîæåñòâî, âîññòàíîâëåííîå

íà îñíîâå ýòîé ôóíêöèè ðàñõîäîâ:

{:(, ) 0},

=∈ ≥ ∀>>

VxRpxepup

òî äëÿ âñåõ

(, ) min .

∈

ep u px

2. Åñëè, êðîìå òîãî, ïðåäïî÷òåíèÿ ïîòðåáèòåëÿ âûïóêëû è ñëàáî

ìîíîòîííû, òî

• Âîññòàíîâëåíèå ïðåäïî÷òåíèé ïî ôóíêöèè ðàñõîäîâ.

Ïóñòü

(, )ep u

 íåïðåðûâíàÿ ôóíêöèÿ, âîçðàñòàþùàÿ ïî u, îä-

íîðîäíàÿ ïåðâîé ñòåïåíè, âîãíóòàÿ è äèôôåðåíöèðóåìàÿ ïî p, òîãäà

(, )ep u

ÿâëÿåòñÿ ôóíêöèåé ðàñõîäîâ äëÿ ïðåäïî÷òåíèé, îïèñûâàåìûõ

ìíîæåñòâàìè

ò.å.

{:(, ) 0}.

=∈ ≥ ∀>>

VxRpxepup

Èçìåðåíèå èçìåíåíèé â áëàãîñîñòîÿíèè ïîòðåáèòåëÿ

Ðàññìîòðèì ýêîíîìè÷åñêóþ ïîëèòèêó, â ðåçóëüòàòå êîòîðîé èç-

ìåíèëñÿ âåêòîð öåí îò

äî

à äîõîä ïîòðåáèòåëÿ îñòàëñÿ ïðåæ-

íèì. Ñîîòâåòñòâóþùåå èçìåíåíèå áëàãîñîñòîÿíèÿ ïîòðåáèòåëÿ â íå-

êèõ ïîñòîÿííûõ öåíàõ

(),p

ìîæíî îöåíèòü êàê ðàçíèöó ðàñõîäîâ:

()()

, ( , ) , ( , ) .

−

epvp I epvp I

Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

Âûáèðàÿ â êà÷åñòâå ñîïîñòàâèìûõ öåí

èñõîäíûå öåíû

, ïî-

ëó÷èì èçìåíåíèå â äîõîäå, íàçûâàåìîå ýêâèâàëåíòíîé âàðèàöèåé

(ñîêðàùåííî EV  equivalent variation):

()()()

01 01 00 01

(, , ) , (, ) , (, ) , (, ) .

=−=−

EVppI epvpI epvpI epvpI I

Èñïîëüçóÿ â êà÷åñòâå ñîïîñòàâèìûõ öåí íîâûå öåíû

ïîëó-

÷èì èçìåíåíèå â äîõîäå, íàçûâàåìîå êîìïåíñèðóþùåé âàðèàöèåé

(ñîêðàùåííî CV  compensating variation):

()()()

01 1 1 1 0 1 0

(, , ) , (, ) , (, ) , (, ).

=−=−

CVppI epvpI epvpI IepvpI

Âîñïîëüçîâàâøèñü ëåììîé Øåïàðäà, ìîæíî èçîáðàçèòü CV è

EV êàê ïëîùàäè ïîä ñîîòâåòñòâóþùèìè êðèâûìè êîìïåíñèðîâàííîãî

ñïðîñà:

00010

(, )

( , ) ( , ) ( , ) ;

∂

==−=

∂

∫∫

ii i

ep u

hpudp dp ep u ep u CV

10111

(, )

(, ) ( , ) ( , ) .

∂

==−=

∂

∫∫

ii i

ep u

hpudp dp ep u ep u EV

• Ñîîòíîøåíèå ìåæäó ýêâèâàëåíòíîé è êîìåíñèðóþùåé

âàðèàöèåé.

Ïóñòü u(

)  íåïðåðûâíàÿ ñòðîãî êâàçèâîãíóòàÿ ôóíêöèÿ ïîëåç-

íîñòè, ïðåäñòàâëÿþùàÿ ëîêàëüíî íåíàñûùàåìûå ïðåäïî÷òåíèÿ ïîòðå-

áèòåëÿ, îïðåäåëåííûå íà ìíîæåñòâå

Ïóñòü öåíû âñåõ òîâà-

ðîâ, êðîìå i-ãî, ôèêñèðîâàíû

(),

−−

à öåíà i-ãî òîâàðà èçìåíÿåò-

ñÿ îò

äî

ïðè÷åì

(, )0

−

ii i

xp p

(, )0.

−

ii i

xp p

Òîãäà:

01 01

( , , ) ( , , ),

CV p p I EV p p I

åñëè òîâàð i-íîðìàëüíûé ïðè

[, ],

∈

iii

ppp

−

è äîõîäå I;

01 01

( , , ) ( , , ),

CV p p I EV p p I

åñëè òîâàð i-èíôåðèîðíûé ïðè

[, ],

∈

iii

ppp

−

è äîõîäå I;

Îñíîâíûå îïðåäåëåíèÿ è óòâåðæäåíèÿ

01 01

( , , ) ( , , ),

CV p p I EV p p I

åñëè òîâàð i-íåéòðàëüíûé ê äî-

õîäó (ò.å. ñïðîñ íà òîâàð íå çàâèñèò îò äîõîäà) ïðè

[, ],

∈

iii

ppp

−

äîõîäå I.

Àãðåãèðîâàíèå â òåîðèè ïîòðåáèòåëÿ

Îïðåäåëèì ñîâîêóïíûé ñïðîñ íà êàæäûé òîâàð êàê ñóììó èíäè-

âèäóàëüíûõ âåëè÷èí ñïðîñà âñåõ ïîòðåáèòåëåé:

( , , , , )

xp I I I

(, ).

xpI

∑

Ñîâîêóïíûé ñïðîñ ÿâëÿåòñÿ ôóíêöèåé îò ñóììàðíîãî äîõîäà

ïîòðåáèòåëåé

, ( , ),







∑∑

kkk

xp I x pI

åñëè êðèâûå «äîõîä  ïî-

òðåáëåíèå» äëÿ âñåõ ïîòðåáèòåëåé ïàðàëëåëüíû.

• Óñëîâèå ïàðàëëåëüíîñòè êðèâûõ «äîõîä  ïîòðåáëåíèå».

Êðèâûå «äîõîä  ïîòðåáëåíèå» äëÿ ðàçíûõ ïîòðåáèòåëåé ïà-

ðàëëåëüíû ïðè ëþáûõ öåíàõ è äîõîäàõ òîãäà è òîëüêî òîãäà, êîãäà

ïðåäïî÷òåíèÿ ïîòðåáèòåëåé ïîðîæäàþò êîñâåííóþ ôóíêöèþ ïîëåç-

íîñòè ôîðìû Ãîðìàíà ñ îäèíàêîâûìè êîýôôèöèåíòàìè ïðè äîõîäàõ:

(, ) () ()

αβ

kkk k

vpI p pI

äëÿ âñåõ

1, 2, , .=

Ôóíêöèÿ ñîâîêóïíîãî ñïðîñà

(, )xp I

óäîâëåòâîðÿåò ñëàáîé àê-

ñèîìå âûÿâëåííûõ ïðåäïî÷òåíèé, åñëè

(, )

≤′′

px p I I

(, )xp I

≠

( ,)xp I

′′

≠

îçíà÷àþò, ÷òî

(, )

>′′

px p I I

äëÿ ëþáûõ

(, )pI

(, ).

′′

Ôóíêöèÿ ñïðîñà

(, )xp I

óäîâëåòâîðÿåò çàêîíó ñïðîñà, åñëè äëÿ

ëþáûõ öåí

′

è äîõîäà I èìååò ìåñòî

()

()(, )(, )ppxpI xpI

′′

−−≤

≤

ïðè÷åì íåðàâåíñòâî áóäåò ñòðîãèì, åñëè

(, ) ( , ).

≠′

xp I xp I

• Óñëîâèå íàñëåäîâàíèÿ ñëàáîé àêñèîìû ïðè àãðåãèðîâàíèè.

Åñëè ôóíêöèè àãðåãèðîâàííîãî ñïðîñà óäîâëåòâîðÿþò çàêîíó

ñïðîñà, òî àãðåãèðîâàííûé ñïðîñ óäîâëåòâîðÿåò ñëàáîé àêñèîìå âû-

ÿâëåííûõ ïðåäïî÷òåíèé.

Ðàçäåë 1. Âûáîð ïîòðåáèòåëÿ â óñëîâèÿõ îïðåäåëåííîñòè

ÇÀÄÀ×È

1.1

Ïðåäïî÷òåíèÿ è ïîëåçíîñòü

1.1.1. Ïîêàæèòå, ÷òî, åñëè íåñòðîãîå îòíîøåíèå ïðåäïî÷òåíèÿ

ðàöèîíàëüíî, òî:

(à) ñòðîãîå îòíîøåíèå ïðåäïî÷òåíèÿ

()

áóäåò àñèììåòðè÷íî,

îòðèöàòåëüíî òðàíçèòèâíî, òðàíçèòèâíî è àöèêëè÷íî;

(á) îòíîøåíèå áåçðàçëè÷èÿ (~) áóäåò ñèììåòðè÷íî è òðàíçèòèâíî.

1.1.2. Ïîêàæèòå, ÷òî åñëè îòíîøåíèå ñòðîãîãî ïðåäïî÷òåíèÿ

àñèììåòðè÷íî è îòðèöàòåëüíî òðàíçèòèâíî, òî îíî ïîñòðîåíî íà îñíî-

âå ðàöèîíàëüíîãî îòíîøåíèÿ íåñòðîãîãî ïðåäïî÷òåíèÿ.

1.1.3. Ïóñòü îòíîøåíèå ïðåäïî÷òåíèÿ

îïðåäåëåííîå íà X,

ðàöèîíàëüíî. Ïîêàæèòå, ÷òî, âûïîëíÿþòñÿ ñëåäóþùèå âàðèàíòû

(îáîáùåííîé) òðàíçèòèâíîñòè:

(à) åñëè x, y, z ∈ X è

(èëè x ~ y) è

,yz

òî

;xz

(á)*

åñëè x, y, z ∈ X è èìåþò ìåñòî ñëåäóþùèå ñîîòíîøåíèÿ

è yz

(èëè y ~ z), òî

;xz

(â) åñëè x, y, z ∈ X è

,xyz

òî

;xz

(ã) åñëè x, y, z ∈X è

,xyz

òî

.xz

1.1.4. Ïîêàæèòå, ÷òî îòíîøåíèå ïðåäïî÷òåíèÿ

çàäàííîå íà

ìíîæåñòâå X, ðàöèîíàëüíî òîãäà è òîëüêî òîãäà, êîãäà êàæäîå êîíå÷-

íîå ïîäìíîæåñòâî ýòîãî ìíîæåñòâà ñîäåðæèò íàèëó÷øèé ýëåìåíò.

1.1.5. Ïîêàæèòå, ÷òî îòíîøåíèå ïðåäïî÷òåíèÿ

çàäàííîå íà

êîíå÷íîì ìíîæåñòâå X, ðàöèîíàëüíî òîãäà è òîëüêî òîãäà, êîãäà ñó-

ùåñòâóåò ôóíêöèÿ ïîëåçíîñòè, ïðåäñòàâëÿþùàÿ ýòè ïðåäïî÷òåíèÿ.

Ê çàäà÷àì (ïóíêòàì), îòìå÷åííûì çâåçäî÷êîé, íà ñ. 227380 ïðèâîäÿòñÿ ïîä-

ðîáíûå ðåøåíèÿ.

Çàäà÷è

1.1.6. Ïîêàæèòå, ÷òî îòíîøåíèå ïðåäïî÷òåíèÿ

çàäàííîå íà

íå áîëåå ÷åì ñ÷åòíîì ìíîæåñòâå X, ðàöèîíàëüíî òîãäà è òîëüêî òîã-

äà, êîãäà ñóùåñòâóåò ôóíêöèÿ ïîëåçíîñòè, ïðåäñòàâëÿþùàÿ ýòè ïðåä-

ïî÷òåíèÿ.

1.1.7. Ïðåäïîëîæèì, ÷òî u(x)  ôóíêöèÿ ïîëåçíîñòè, ïðåäñòàâ-

ëÿþùàÿ ïðåäïî÷òåíèÿ

Âåðíû ëè ñëåäóþùèå óòâåðæäåíèÿ?

(à) Eñëè ôóíêöèÿ ïîëåçíîñòè íåïðåðûâíà, òî ïðåäïî÷òåíèÿ íå-

ïðåðûâíû.

(á) Åñëè ïðåäïî÷òåíèÿ íåïðåðûâíû, òî ôóíêöèÿ ïîëåçíîñòè íå-

ïðåðûâíà.

(â) Åñëè ôóíêöèÿ ïîëåçíîñòè ìîíîòîííà (ñòðîãî ìîíîòîííà), òî

ïðåäïî÷òåíèÿ ìîíîòîííû (ñòðîãî ìîíîòîííû).

(ã) Åñëè ïðåäïî÷òåíèÿ ìîíîòîííû (ñòðîãî ìîíîòîííû), òî ôóíê-

öèÿ ïîëåçíîñòè ìîíîòîííà (ñòðîãî ìîíîòîííà).

(ä)* Åñëè ôóíêöèÿ ïîëåçíîñòè âîãíóòà (ñòðîãî âîãíóòà), òî ïðåä-

ïî÷òåíèÿ âûïóêëû (ñòðîãî âûïóêëû).

(å)* Åñëè ïðåäïî÷òåíèÿ âûïóêëû (ñòðîãî âûïóêëû), òî ôóíêöèÿ

ïîëåçíîñòè âîãíóòà (ñòðîãî âîãíóòà).

1.1.8. Êàêèå èç íèæåñëåäóþùèõ ôóíêöèé ïðåäñòàâëÿþò òå æå

ïðåäïî÷òåíèÿ, ÷òî è ôóíêöèÿ u(x), â ïðåäïîëîæåíèè, ÷òî ôóíêöèÿ u(x)

ïðèíèìàåò çíà÷åíèÿ ðàçíûõ çíàêîâ?

(à)

()

() () .

ux ux

(á)

( ) 10.

(â)

( ) 10.

−

(ã)

()

1/3

() .

(ä)

()

exp ( ) .ux

(å)

()

exp ( ) .

−−

1.1.9. Ïðè êàêèõ çíà÷åíèÿõ ïàðàìåòðà α íèæåñëåäóþùèå ôóíê-

öèè ïðåäñòàâëÿþò òå æå ïðåäïî÷òåíèÿ, ÷òî è ôóíêöèÿ u(x), åñëè èçâå-

ñòíî, ÷òî ôóíêöèÿ u(x) ïðèíèìàåò òîëüêî ïîëîæèòåëüíûå çíà÷åíèÿ?

(à)

()

() .