Burton T. (et. al.) Wind energy Handbook

Подождите немного. Документ загружается.

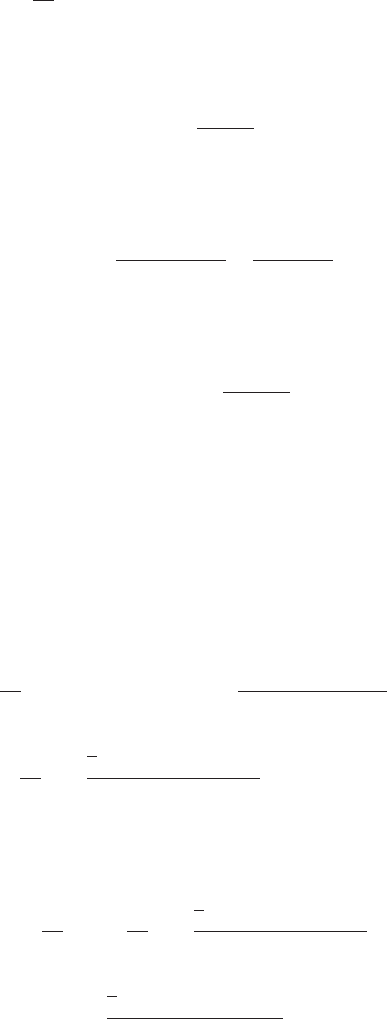
where (W 3 ˆ) is a vector product.

Q ¼ rW 3 ˆ r sin 

¼ rˆrU

(1  a)(3:35)

Equating the two expressions gives

a9 ¼

4r



Hence

a(1  a)



(1 þ a9

)

a(1  a)

(1 þ a9

)

(1 þ a9

) ¼

a(1  a)

(3:36)

Equation (3.36) is not quite the same as Equation (3.23) of Section 3.3.3 and it can be

shown that this is a result of ignoring the wake expansion.

3.4.5 Torque and power

The torque on an annulus of radius r and radial width r is

Qr ¼ rWˆ r sin 

r ¼

r4rU

a(1  a)

(1 þ a9

)

r

Q ¼

2r4a(1  a)

(1 þ a9

)

(3:37)

Power

P ¼ 

Q ¼

2r4a(1  a)

(1 þ a9

)

(3:38)

P ¼

R

4a(1  a)

(1 þ a9

)

(3:39)

VORTEX CYLINDER MODEL OF THE ACTUATOR DISC 55

Power coefﬁcient

4a(1  a)

(1 þ a9

)

¼ 4a9

(1  a)

(3:40)

The reduced efﬁciency compared with the simple actuator disc result, C

4a(1  a)

, is caused by the energy required to spin the wake, as a rigid body, with

an angular velocity 2a9

. It should be noted that any additional rotational energy is

accounted for by the loss of static pressure caused by the pressure gradient wh ich

balances the centrifugal forces on the rotating ﬂuid.

The general momentum theory of Glauert (1935a) includes the expansion of the

wake and shows that no contribution at all is actually required from the kinetic

energy of the free-stream ﬂow to maintain wake rotation; all the kinetic energy of

rotation is deriv ed from static pressure energy.

3.4.6 Axial ﬂow ﬁeld

By means of the Biot-Savart law the induced velocity in the wind-wise (axial)

direction at the actuator disc can be determined both upstream of the disc and

downstream in the developing wake, as well as on the disc itself. The ﬂow ﬁeld (net

velocity) is axisymmetric and a radial cross section is shown in Figure 3.9. Both

radial and axial distances are divided by the disc radius with the axial distance

being measured downstream from the disc and the radial distance being measured

from the rotational axis. The velocity is divided by the wind speed.

The axial velocity within the wake is sharply lower than without and is radially

uniform at the disc and in the far wake, just as the momentum theory predicts.

There is a small acceleration of the ﬂow immediately outside of the wake. The

induced velocity on the wake cylinder itself is

a at the disc and a in the far wake.

0.8

0.6

0.4

0.2

-1

1.5

0.5

-1

0.8

0.6

0.4

0.2

Radial distance

Axial distance

Axial flow

velocity

-2

0.5

1.5

-2

Figure 3.9 The Radial and Axial Variation of Axial Velocity in the Vicinity of an Actuator

Disc, a ¼ 1=3

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

3.4.7 Tangential ﬂow ﬁeld

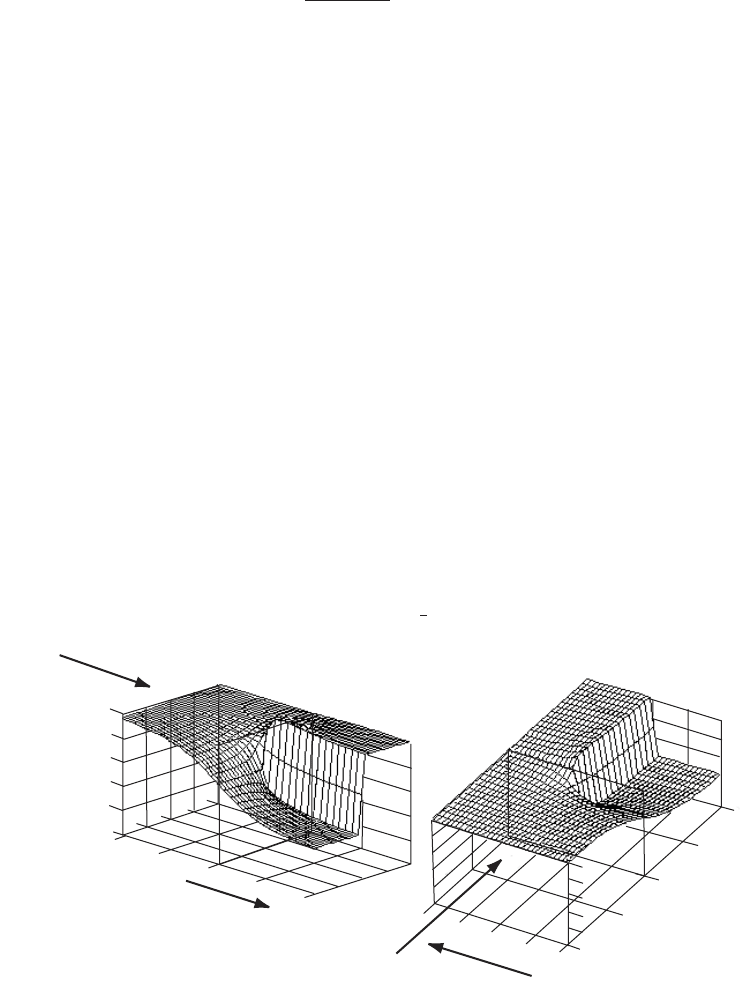
The tangential induce d v elocity is determined not only by the root vortex but also

by the component of vorticity g sin  on the wake cylinder and the bound vorticity

on the rotor disc. At a radial distance equal to half the disc radius, as an example,

the axial variation of the three contributions are shown in Figure 3.10.

The bound vorticity causes rotation in opposite senses upstream and downstream

of the disc with a step change across the disc. The upstream rotation, which is in the

same sense as the rotor rotation, is nulliﬁed by the root vortex, which induces

rotation in the opposite sense to that of the rotor. The downstream rotation is in the

same sense for both the root vortex and the bound vorticity the stream-wise

variations of the two summing to give a uniform velocity in the stream-wise sense.

The vorticity located on the surface of the wake cylinder makes a small contri -

bution.

At the disc itself the bound vorticity induces no rotation, see Figure 3.10, the

wake cylinder ind uces no rotation either and so it is only the root vortex which does

induce rotation and that value is half the total induced generally in the wake. It is

now clear why only half the rotational velocity is used to determi ne the ﬂow angle

at the disc.

The rotational ﬂow is conﬁned to the wake, that is, inside the cylinder. There is

no rotational ﬂow anyw here outside of the wake, neither upstream of the disc or

outside the cylinder. The rotational velocity within the cylinder falls with increasing

radius but is not zero at the outer edge of the wake, therefore there is an abrupt fall

of rotational velocity across the cylindrical surface. The contri butions of the three

vorticity sources to the rotational ﬂow at a radius of 101 percent of the disc radius

are shown in Figure 3.11; the total rotational ﬂow is zero at all axial positions but

the individual components are not zero.

0.06

0.04

0.02

-0.02

-0.04

-1 -0.5 0 0.5 1

Root vortex

Total

Bound vortex

Vortex cylinder

Axial distance

Tangential flow induction factor

Figure 3.10 The Axial Variation of Tangential Velocity in the Vicinity of an Actuator Disc at

50% Radius, a ¼ 1=3, º ¼ 6

VORTEX CYLINDER MODEL OF THE ACTUATOR DISC 57

3.4.8 Radial ﬂow ﬁeld

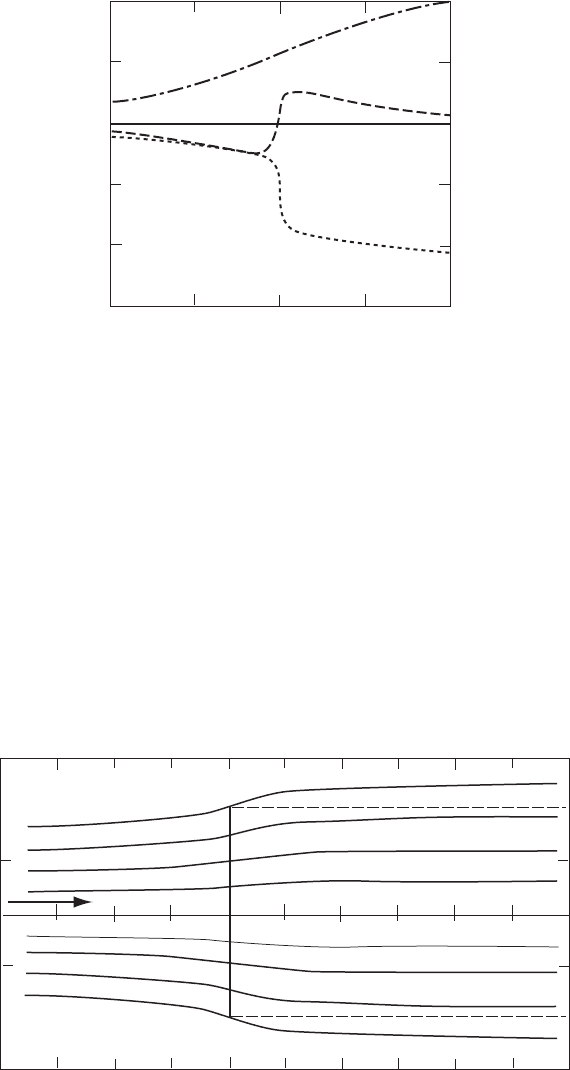
Although the vor tex cylinder theory has been simpliﬁed by not allowing the

cylinder to expand, nevertheless the theory predicts ﬂow expansion. A radial

velocity distribution is predicted by the theory as shown in Figure 3.12 which

shows a longitudinal section of the ﬂow ﬁeld through the rotor disc.

The radial velocity, as calculated, is greatest as the ﬂow passes through the rotor

disc and, although not shown in Figure 3.12, it is inﬁnite at the edge of the disc. The

situation is very similar to the determination of the potential ﬂow ﬁeld around a

ﬂat, solid, circular disc which is normal to the oncoming ﬂow; an inﬁnite radial

−1 −0.5 0 0.5 1

0.01

0.005

-0.005

-0.01

-0.015

Axial distance

Tangential flow induction factor

Figure 3.11 The Axial Variation of Tangential Velocity in the Vicinity of an Actuator Disc at

101 percent Radius, a ¼ 1=3, º ¼ 6

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3

1.5

0.5

1.5

—

Figure 3.12 Flow Field Through an Actuator Disc for a ¼ 1=3

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

velocity is predicted at the disc edge for the ﬂow to pass around and continue

radially inwards on the downstream side. In practice there would be insufﬁcient

static pressure available to fuel an inﬁnite, or even a very high, velocity and so some

discontinuity in the ﬂow must occur. The presence of even the smallest amount of

viscosity would produce a thick boundary layer towards the disc edge because of

the high radial velocity. The viscosity in the boundary layer would absorb mu ch of

the available energy and dissipate it as heat so that as the ﬂow accelerated around

the disc edge the maximum velocity attainable would be limited by the static

pressure approaching zero. Instead of the ﬂow moving around the edge it would

separate from the edge and continue downstream leaving a very low pressure

region behind the disc with very low velocity —a stagnant region.

In the case of the permeable rotor disc there would be some ﬂow through the

disc, which would behave as described above, but the separation of the ﬂow at the

disc edge would produce an additional low pressure in the wake.

The problem of the inﬁnite radial velocity at the rotor disc edge arises because of

the assumption of an inﬁnite number of rotor blades. If the theory is modiﬁed such

that there are only a few blades the inﬁnite radial velocity disappears. However, if,

for a given rotor, the tip speed ratio is increased, with a consequent increase of the

axial ﬂow induction factor, the radial velocity at the tip rises sharply and the

problem of edge separation returns, which is wh at actually occurs, see Section 3.6.

3.4.9 Conclusions

Despite the exclusion of wake expansion, the vortex theory produces results largely

in agreement with the momentum theory and enlightens understanding of the ﬂow

through an energy extracting actuator disc.

3.5 Rotor Blade Theory

3.5.1 Introduction

The aerodynamic lift (and drag) forces on the span-wise elements of radius r and

length r of the several blades of a wind turbine rotor are responsible for the rate of

change of axial and angular momentum of all of the air which passes through the

annulus swept by the blade elements. In addition , the force on the blade elements

caused by the drop in pressure associated with the rotational velocity in the wake

must also be provided by the aerodynam ic lift and drag. As there is no rotation of

the ﬂow approaching the rotor the reduced pressure on the downwind side of the

rotor caused by wake rotation appears as a step pressure drop just like that which

causes the change in axial momentum. Because the wake is still rotating in the far

wake the pressure drop caused by the rotation is still present and so does not

contribute to the axial momentum change.

ROTOR BLADE THEORY 59

3.5.2 Blade element theory

It is assumed that the forces on a blade element can be calculated by means of two-

dimensional aerofoil characteristics using an angle of attack determined from the

incident resultant velocity in the cross-sectional plane of the element; the velocity

component in the span-wise direction is ignored. Three-dimensional effects are also

ignored.

The velocity components at a radial position on the blade expressed in terms of

the wind speed, the ﬂow factors and the rotational speed of the rotor will determine

the angle of attack. Having information about how the aerofoil characteristic coefﬁ-

cients C

and C

vary with the angle of attack the forces on the blades for given

values of a and a9 can be determined.

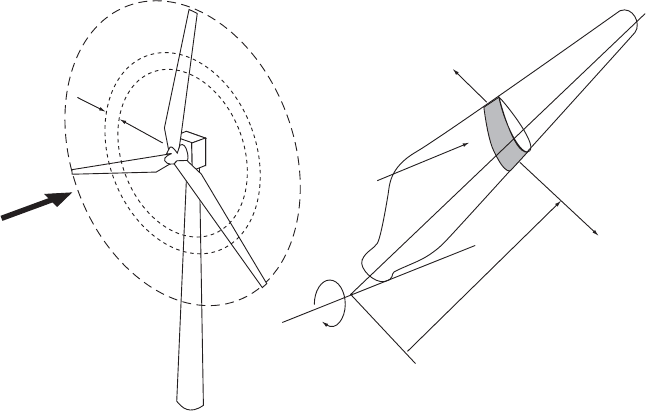
Consider a turbine with N blades of tip radius R each with chord c and set pitch

angle  measured between the aerofoil zero lift line and the plane of the disc. Both the

chord length and the pitch angle may vary along the blade span. Let the blades be

rotating at angular velocity  and let the wind speed be U

. The tangential veloci ty

r of the blade element shown in Figure 3.13 combined with the tangential velocity

of the wake a9 r means that the net tangential ﬂow velocity experienced by the

blade element is (1 þ a9)r. Figure 3.14 shows all the velocities and forces relative

to the blade chord line at radius r.

From Figure 3 .14 the resultant relative velocity at the blade is

W ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

(1  a)

þ 

(1 þ a9)

(3:41)

which acts at an angle  to the plane of rotation, such that

Ωra'

Ωr

Ω

(1-a)

δr

Figure 3.13 A Blade Element Sweeps Out an Annular Ring

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

sin  ¼

(1  a)

and cos  ¼

r(1 þ a9)

(3:42)

The angle of attack Æ is then given by

Æ ¼    (3:43)

The lift force on a span-wise length r of each blade, normal to the direction of W,is

therefore

L ¼

cCr (3:44)

and the drag force parallel to W is

D ¼

rr (3:45)

3.5.3 The blade element – momentum (BEM) theory

The basic assumption of the BEM theory is that the force of a blade element is solely

responsible for the change of momentum of the air which passes through the

annulus swept by the element. It is therefore to be assumed that there is no radial

interaction between the ﬂows through contiguous annuli—a condition that is,

strictly, only true if the axial ﬂow induction factor does not vary radially. In

practice, the axial ﬂow induction factor is seldom uniform but experimental

examination of ﬂow through propeller discs by Lock (1924) shows that the assump-

tion of radial independence is acceptable.

The component of aerodynamic force on N blade elements resolved in the axial

direction is

L cos  þ D sin  ¼

Nc(C

cos  þ C

sin )r (3:46)

∞

(1-a)

Ωr(1+a)

Lcos φ + D sin φ

L sin φ − D cos φ

(

)

Velocities

(

)

Forces

Figure 3.14 Blade Element Velocities and Forces

ROTOR BLADE THEORY 61

The rate of change of axial momentum of the air passing through the swept annulus

(1  a)2rr2aU

¼ 4rU

a(1  a)rr (3:47)

The drop in wake pressure caused by wake rotation is equal to the increase in

dynamic head, which is

r(2a9 r)

Therefore the additional axial force on the annulus is

r(2a9 r)

2rr

Thus

Nc(C

cos  þ C

sin )r ¼ 4r[U

a(1  a) þ (a9 r)

]rr

Simplifying,

cos  þ C

sin ) ¼ 8(a(1  a) þ (a9º)

) (3:48)

The element of axial rotor torque caused by aerodynamic forces on the blade

elements is

(L sin    D cos )r ¼

Nc(C

sin   C

cos )rr (3:49)

The rate of change of angular momentum of the air passing through the annulus is

(1  a)  r2a9r2rr ¼ 4rU

(r)a9(1  a)r

r

Equating the two moments

Nc(C

sin   C

cos )rr ¼ 4rU

(r)a9(1  a)r

r (3:50)

Simplifying,

sin   C

cos ) ¼ 8º

a9(1  a)(3:50a)

where the parame ter  ¼ r =R.

62 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

It is convenient to put

cos  þ C

sin  ¼ C

and

sin   C

cos  ¼ C

Solving Equations 3.48 and (3.50a ) to obtain values for the ﬂow indu ction factors a

and a 9 using two-dimensional aerofoil characteristics requires an iterative process.

The following equations, derived from (3.48) and (3.50a), are conve nient in which

the right-hand sides are evaluated using existing values of the ﬂow induction

factors yielding simple equations for the next iteration of the ﬂow induction factors.

1  a



4 sin 

) 



4 sin





(3:51)

1 þ a9



4 sin  cos 

(3:52)

Blade solidity  is deﬁned as total blade area divided by the rotor disc area and is a

primary parameter in determining rotor performance. Ch ord solidity 

is deﬁned

as the total blade chord length at a given radius divided by the circumferential

length at that radius.



2

2

(3:53)

It is argu ed by Wilson and Lissaman (1974) that the drag coefﬁcient should not be

included in Equations (3.51) and (3.52) because the velocity deﬁcit caused by drag is

conﬁned to the narrow wake which ﬂows from the trailing edge of the aerofoil.

Furthermore, Wilson and Lissaman reason, the drag-based velocity deﬁcit is only a

feature of the wake and does not contribute to the velocity deﬁcit upstream of the

rotor disc. The basis of the argument for excluding drag in the determination of the

ﬂow induction factors is that, for attached ﬂow, drag is caused only by skin friction

and does not affect the pressure drop across the rotor. Clearly, in stalled ﬂow the

drag is overwhelmingly caused by pressure. In attac hed ﬂow it has been shown by

Young and Squire (1938) that the modiﬁcation to the inviscid pressure distribution

around an aerofoil caused by the boun dary layer has an affect both on lift and drag.

The ratio of pressure drag to total drag at zero angle of attack is approximately the

same as the thickness to chord ratio of the aerofoil and increases as the angle of

attack increases.

One last point about the BEM theory: the theory is strictly only applicable if the

blades have uniform circulation, i.e., if a is uniform. For non-uniform circulation

there is a radial interaction and exchange of moment um between ﬂows through

adjacent elemental annular rings. It cannot be stated that the only axial force acting

ROTOR BLADE THEORY 63

on the ﬂow through a given annular ring is that due to the pressure drop across the

disc. However, in practice, it appears that the error involved in relaxing the above

constraint is small for tip speed ratios greater than 3.

3.5.4 Determination of rotor torque and power

The calculation of torque and power developed by a rotor requires a knowledge of

the ﬂow induction factors, which are obtained by solving Equations (3.51) and

(3.52). The solution is usually carried out iteratively because the two-dimensional

aerofoil characteristics are non-linea r functions of the angle of attack.

To determine the complete performance characteristic of a rotor, i.e., the manner

in which the power coefﬁcient varies over a wide range of tip speed ratio, requires

the iterative solution. The iterative procedure is to assume a and a9 to be zero

initially, determining , C

and C

on that basis, and then to calculate new values

of the ﬂow factors using Equations (3.51) and (3.52). The iteration is repeated until

convergence is achieved.

From Equation (3.50) the torque developed by the blade elements of span-wise

length r is

Q ¼ 4  rU

(r)a9(1  a)r

r

If drag, or part of the drag, has been excluded from the determination of the ﬂow

induction factors then its effect must be introduced when the torque caused by drag

is calculated from blade element forces, see Equation (3.49),

Q ¼ 4  rU

(r)a9(1  a)r

r 

NcC

cos()rr

The complete rotor, therefore, develops a total torque Q:

Q ¼

R



8a9(1  a) 



(1 þ a9)

d

(3:54)

The power developed by the rotor is P ¼ Q. The power coefﬁcient is

R

Solving the BEM Equations (3.51) and (3.52) for a given, suitable blade geometrical

and aerodynamic design yields a series of values for the power and torque coefﬁ-

cients which are functions of the tip speed ratio. A typical performance curve for a

modern, high-speed wind turbine is shown in Figure 3.15.

The maximum power coefﬁcient occurs at a tip speed ratio for which the axial

ﬂow induction factor a, which in general varies with radius, approximates most

64 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES