Burton T. (et. al.) Wind energy Handbook

Подождите немного. Документ загружается.

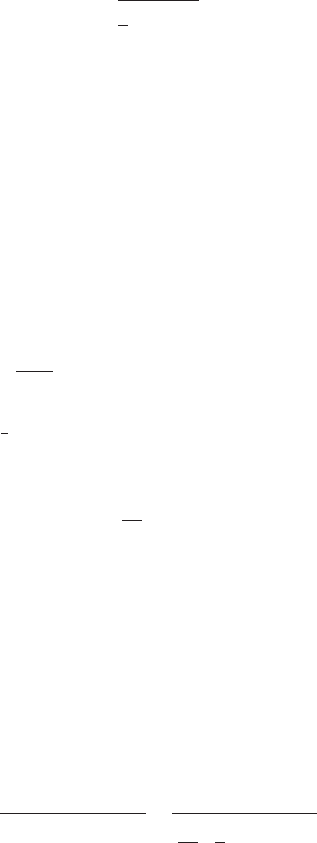
As this force is concentrated at the actuator disc the rate of work done by the force

is FU

and hence the power extractio n from the air is given by

Power ¼ FU

¼ 2rA

a(1  a)

(3:10)

A power coefﬁcient is then deﬁned as

Power

(3:11)

where the denominator represents the power available in the air, in the absence of

the actuator disc. Therefore,

¼ 4a(1  a)

(3:12)

3.2.3 The Betz limit

The maximum value of C

occurs when

¼ 4(1  a)(1  3a) ¼ 0

which gives a value of a ¼

Hence,

max

¼ 0:593 (3:13)

The maximum achievable value of the power coefﬁcient is known as the Betz

limit after Albert Betz the German aerodynamicist (119) and, to date, no wind

turbine has been designed which is capable of exceeding this limit. The limit is

caused not by any deﬁciency in design, for, as yet, we have no design, but because

the stream-tube has to expand upstream of the actuator disc and so the cross section

of the tube where the air is at the full, free-stream velocity is smaller than the area

of the disc.

could, perhaps, more fairly be deﬁned as

Power extracted

Power available

Power extracted



(3:14)

but this not the accepted deﬁnition of C

THE ACTUATOR DISC CONCEPT 45

3.2.4 The thrust coefﬁcient

The force on the actuator disc caused by the pressure drop, given by Equation (3.9),

can also be non- dimensionalized to give a Coefﬁcient of Thrust C

Power

(3:15)

¼ 4a(1  a)(3:16)

A problem arises for values of a >

because the wake velocity, given by

(1  2a)U

, becomes zero, or even negative; in these conditions the mo mentum

theory, as described, no longer applies and an empirical modiﬁcation has to be

made (Section 3.5).

The variation of power coefﬁcient and thr ust coef ﬁcient with a is shown in Fig-

ure 3.3.

3.3 Rotor Disc Theory

The manner in which the extracte d energy is converted into usable energy depends

upon the particular turbine design. Most wind energy converters employ a rotor

with a number of blades rotating with an angular velocity  about an axis normal

to the rotor plane and parallel to the wi nd direction. The blades sweep out a disc

and by virtue of their aerodynamic design develop a pressure difference across the

disc, which, as discussed in the previous sec tion, is responsible for the loss of axial

momentum in the wake. Associated with the loss of axial momentum is a loss of

energy which can be collected by, say, an electrical generator attached to the rotor

shaft if, as well as a thrust, the rotor experiences a torque in the direction of rotation.

The generator exerts a torque equal and opposite to that of the airﬂow which keeps

the rotational speed constant. The work done by the aerodynamic torque on the

generator is converted into electrical energy. The required aerodynamic design of

the rotor blades to provide a torque as well as a thrust is discussed in Section 3.5.

(a)

0.5

0 0.2 0.4 0.6 0.8 1

Figure 3.3 Variation of C

and C

with Axial Induction Factor a

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

3.3.1 Wake rotation

The exertion of a torque on the rotor disc by the air passing through it requires an

equal and opposite torque to be imposed upon the air. The consequence of the

reaction torque is to cause the air to rotate in a direction opposite to that of the rotor;

the air gains angular momentum and so in the wake of the rotor disc the air

particles have a velocity component in a direction which is tangential to the rotation

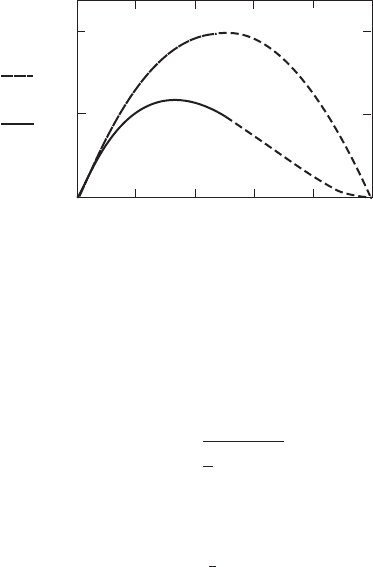
as well as an axial component (Figure 3.4).

The acquisition of the tangential component of velocity by the air means an

increase in its kinetic energy which is compensated for by a fall in the static

pressure of the air in the wake in addition to that which is described in the previous

section.

The ﬂow entering the actuator disc has no rotational motion at all. The ﬂow

exiting the disc does have rotation and that rotation remains constant as the ﬂuid

progresses down the wake. The transfer of rotational motion to the air takes place

entirely across the thickness of the disc (see Figure 3.5). The change in tangential

velocity is expressed in terms of a tangential ﬂow induction factor a9. Upstream of

the disc the tangenti al velocity is zero. Immediately downstream of the disc the

tangential velocity is 2ra9. At the middle of the disc thickness, a radial distance r

from the axi s of rotation, the induced tangential velocity is  ra9. Because it is

produced in reaction to the torque the tangential velocity is opposed to the motion

of the rotor.

An abrupt acquisition of tangential velocity cannot occur in practice. Figure 3.5

shows the ﬂow accelerating in the tangential direction as it is ‘squeezed’ between

the blades; the separation of the blades has been reduced for effect but it is the

increasing solid blockage that the blades present to the ﬂow as the root is ap-

proached that causes the high values of tangential velocity close to the root.

3.3.2 Angular momentum theory

The tangential velocity will not be the same for all radial positions and it may well

also be that the axial induced velocity is not the same. To allow for variation of both

induced velocity components consider only an annular ring of the rotor disc which

is of radius r and of radial width r.

The increment of rotor torque acting on the annular ring will be responsible for

Ω

Figure 3.4 The Trajectory of an Air Particle Passing Through the Rotor Disc

ROTOR DISC THEORY 47

imparting the tangential velocity component to the air whereas the axial force acting

on the ring will be responsible for the reduction in axial velocity. The whole disc

comprises a multiplicity of annular rings and each ring is assumed to act indepen-

dently in imparting momentum only to the air which actually passes through the

ring.

The torque on the ring will be equal to the rate of change of angular momentum

of the air passing through the ring. Thus,

torque ¼ rate of change of angular momentum

¼ mass flow rate 3 change of tangential velocity 3 radius

Q ¼ rA

(1  a)2 a9r

(3:17)

where A

is taken as being the area of an annular ring.

The driving torque on the rotor shaft is also Q and so the increment of rotor

shaft power outpu t is

P ¼ Q

The total power extracted from the wind by slowing it down is therefore deter-

mined by the rate of change of axial momentum given by Equation (3.10) in Section

3.2.2

2a'Ωr

ρ(2a'Ωr)

∞

(1-a)

∞

(1-a)

∞

(1-a)

a'Ωr

Ωr

Rotor motion

Figure 3.5 Tangential Velocity Grows Across the Disc Thickness

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

P ¼ 2rA

a(1  a)

Hence

2rA

a(1  a)

¼ rA

(1  a)2 

a9r

and

a(1  a) ¼ 

r is the tangential velocity of the spinning annular ring and so º

¼ r=U

called the local speed ratio. At the edge of the disc r ¼ R and º ¼  R=U

is known

at the tip speed ratio. Thus

a(1  a) ¼ º

a9 (3:18)

The area of the ring is A

¼ 2rr therefore the incremental shaft power is, from

Equation (3.17),

P ¼ dQ ¼

2rr



4a9(1  a)º

The term in brackets represents the power ﬂux through the annulus, the term

outside the brackets, therefore, is the efﬁciency of the blade eleme nt in capturing

the power, or blade element efﬁciency:



¼ 4a9(1  a)º

(3:19)

In terms of power coefﬁcient

4rU

(1  a)a9º

R

8(1  a)a9º

d

¼ 8(1  a)a9º



(3:20)

where  ¼ r=R.

Knowing how a and a9 vary radially, Equation (3.20) can be integrated to

determine the overall power coefﬁcient for the disc for a given tip speed ratio, º.

3.3.3 Maximum power

The values of a and a9 which will provide the maximum possible efﬁciency can be

determined by differentiating Equation (3.19) by either factor and putting the result

equal to zero. Whence

da9

a ¼

1  a

(3:21)

ROTOR DISC THEORY 49

From Equation (3.18)

da9

a ¼

1  2a

giving

a9º

¼ (1  a)(1  2a )(3:22)

The combination of Equations (3.18) and (3.21) gives the required values of a and a9

which maximize the incremental power coefﬁcient:

a ¼

and a9 ¼

a(1  a)



(3:23)

The axial ﬂow induction for maximum power extraction is the same as for the non-

rotating wake case, that is, a ¼

and is uniform over the entire disc. On the other

hand a9 varies with radial position.

From Equation (3.20) the maximum power is

8(1  a)a9º



d

Substituting for the expressions in Equations (3.23)

8(1  a)

a(1  a)







d ¼ 4a(1  a)

(3:24)

Which is precisely the same as for the non-rotatin g wake case.

3.3.4 Wake structure

The angular momentum imparted to the wake increases the kinetic energy in the

wake but this energy is balanced by a loss of static pressure:

˜ p

r(2a9 r)

(3:25)

Substituting the expression for a9 given by Equations (3.23)

˜ p

a(1  a )

º



(3:26)

The tangential velocity increases with decreasing radius (Equation (3.23)) and so

the pressure decreases creating a radial pressure gradient. The radial pressure

gradient balances the centrifugal force on the rotating ﬂuid. The pressure drop

50 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

across the disc caused by the rate of change of axial momentum as developed in

Section 3.2.1 (Equation (3.9)) is additional to the pressure drop associated with the

rotation of the wake and is uniform over the whole disc.

If the wake did not expand as it slows down the rotational wake structure

together with the rotational pressure gradient would not change as the wake

develops whereas the pressure loss caused by the change of axial momentum will

gradually reduce to zero in the fully-developed wake, as shown in Figure 3.2. The

pressure in the fully developed wake would therefore be atmospheric super-

imposed on which would be the pressure loss given by Equation (3.26). Conse-

quently, the axial force on the ﬂuid in the wake causing it to slow down would be

only that caused by the uniform pres sure drop across the disc given by Equation

(3.9), as is assumed in the simple theory of Section 3.2.1. The rotational pressure

drop does not contribute to the change of axial momentum.

In fact, the wake does expand and the full details of the analysis are given by

Glauert (1935a). Glauert’s analysis is applied to propellers where the ﬂow is

accelerated by the rotor but this is only a matter of reve rsing the signs of the ﬂow

induction factors. The inclusion of ﬂow expansion and wake rotation in a fully

integrated momentum theory shows that the axial induced velocity in the devel -

oped wake is greater than 2a but the effect is only signiﬁcant at tip spee d ratios less

than about 1.5, which is probably outside of the operating range for most modern

wind turbines. The analysis does, however, demonstrate that the kinetic energy of

wake rotation is accounted for by reduced static pressure in the wake. Glauert’s

conclusion about wake expansion and its interaction with wake rotation is that its

inclusion makes little difference to the results obtained from the simple axial

momentum theory and so can be ignored. Where, in the same reference, Glauert

deals with ‘Windmills and Fans’ (1935b) he adopts the simple momentum theo ry

but then has to account for kinetic energy of wake rotation, which he does by

assuming that it is drawn from the kinetic energy of the ﬂow. The rotational kinetic

energy of the wake is therefore regarded as a loss and reduces the level of the

energy that can be extracted. Consequently, at low local speed ratios, the inboard

sections of a rotor, the local aerodynamic efﬁciency falls below the Betz limit. Most

authors since Glauert have assumed the same conclusion but, in fact, Glauert

himself has demonstrated that the conclusion is wrong. The error makes very little

difference to the ﬁnal results for most modern wind turbines designed for the

generation of electricity. For wind pumps, where a high starting torque and high

solidity are required, the error would probably be very signiﬁcant because they

operate at very low tip speed ratios.

3.4 Vortex Cylinder Model of the Actuator Disc

3.4.1 Introduction

The momentum theory of Section 3.1 uses the concept of the actuator disc across

which a pressure drop develops constituting the energy extracted by the rotor. In

the rotor disc theory of Section 3.3 the actuator disc is depicted as being swept out

VORTEX CYLINDER MODEL OF THE ACTUATOR DISC 51

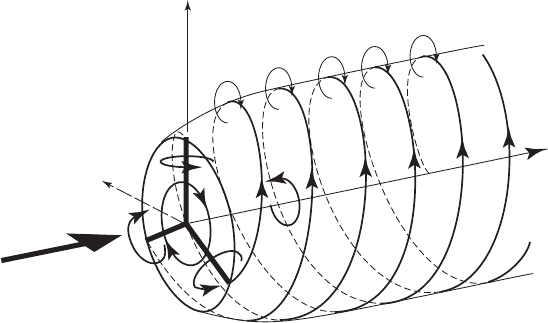
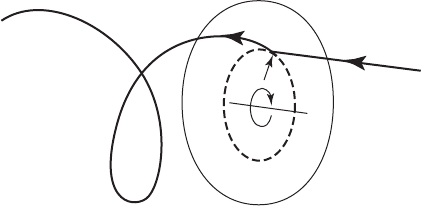
by a multiplicity of aerofoil blades each with radially uniform bound circulation

˜ˆ. From the tip of each blade a helical vortex of strength ˜ˆ convects downstream

with the local ﬂow velocity (Figure 3.6). If the number of blades is assume d to be

very large but the solidity of the total is ﬁnite and small then the accumulation of

helical tip vortices will form the surface of a tube. As the number of blades

approaches inﬁnity the tube surface will become a continuous tubular vortex sheet.

From the root of each blade, assuming it reaches to the axis of rotation, a line

vortex of strength ˜ˆ will extend downstream along the axis of rotation contribut-

ing to the total root vortex of strength ˆ. The vortex tube will expand in radius as

the ﬂow of the wake inside the tube slows down. Vorticity is conﬁned to the surface

of the tube, the root vortex and to the bound vortex sheet swept by the multiplicity

of blades to form the rotor disc; elsewhere in the wake and everywhere else in the

entire ﬂow ﬁeld the ﬂow is irrotational.

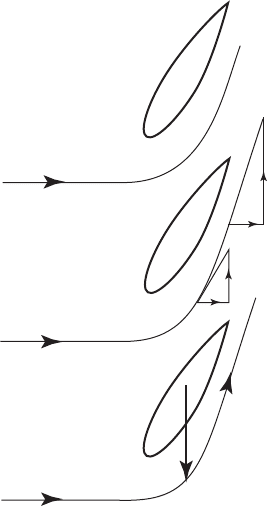
The nature of the tube’s expansion cannot be determined by means of the

momentum theory and so, as an approximation, the tube is allowed to remain

cylindrical Figure 3.7. The Biot–Savart law is used to determine the induced

velocity at any point in the vicinity of the actuator disc. The cylindrical vortex

model allows the whole ﬂow ﬁeld to be determined and is accurate within the

limitations of the non-expanding cylindrical wake.

3.4.2 Vortex cylinder theory

The vortex cylinder has surface vorticity which follows a helical path with a helix

angle  or, as it has been termed previously, the ﬂow angle at the blade tip. The

strength of the vorticity is g ¼ dˆ=dn, where n is a direction in the tube surface

normal to the direction of ˜ˆ, and has a component g

¼ g cos 

parallel to the

rotor disc. Due to g

the axial (parallel to the axis of rotor rotation) induced velocity

at the rotor plane is uniform over the rotor disc and can be determined by means of

the Biot–Savart law as

∆Γ

Ω

∞

Figure 3.6 Helical Vortex Wake Shed by Rotor with Three Blades Each with Uniform

Circulation ˜ˆ

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

¼

¼aU

(3:27)

In the far wake the axial induced velocity is also uniform within the cylindrical

wake and is

¼g

¼2aU

(3:28)

The ratio of the two induced velocities corresponds to that of the simple momentum

theory and justiﬁes the assumpti on of a cylindrical vortex sheet.

3.4.3 Relationship between bound circulation and the induced

velocity

The total circulation on all of the multiplicity of blades is ˆ which is shed at a

uniform rate into the wake in one revolution. So, from Figure 3.8 in which the

cylinder has been slit longitudinally and opened out ﬂat,

∆Γ

∞

Figure 3.7 Simpliﬁed Helical Vortex Wake Ignoring Wake Expansion

∆Γ =

dΓ

δn

δs

2 R

Figure 3.8 The Geometry of the Vorticity in the Cylinder Surface

VORTEX CYLINDER MODEL OF THE ACTUATOR DISC 53

g ¼

2R sin(

)

(3:29)

hence

2R

cos 

sin 

2

R(1 þ a9

)

(1  a)

(3:30)

therefore

2aU

2R

R(1 þ a9

)

(1  a)

(3:31)

So, the total circulation is rela ted to the induced velocity

ˆ ¼

4U

a(1  a)

(1 þ a9

)

(3:32)

3.4.4 Root vortex

Just as a vortex is shed from each blade tip a vortex is also shed from each blade

root. If it is assumed that the blades extend to the axis of rotation, obviously not a

practical option, then the root vortices will each be a line vortex running axially

downstream from the centre of the disc. The direction of rotation of the all the root

vortices will be the same forming a core, or root, vortex, of total strength ˆ. The root

vortex is primarily responsible for induci ng the tangential velocity in the wake ﬂow

and in particular the tangential velocity on the rotor disc.

On the rotor disc surface the tangential velocity induced by the root vortex, given

by the Biot–Savart law, is

ra9 ¼

4r

a9 ¼

4r



(3:33)

This relationship can also be derived from the momentum theory: the rate of change

of angular momentum of the air which passes through an annulus of the disc of

radius r and radial width dr is equal to the torque increment imposed upon the

annulus

dQ ¼ rU

(1  a)2 r dr2a9r

(3:34)

By the Kutta–Joukowski theorem the lift per unit radial width is

L ¼ r(W 3 ˆ)

54 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES