Burton T. (et. al.) Wind energy Handbook

Подождите немного. Документ загружается.

The apparent A-weighted sound pow er level of the turbine is then calculated

from

WA,ref

¼ L

Aeq,ref

þ 10 log

(4R

)  6(9: 18)

where R

is the slant distance from the microphone to the wind turbine hub.

It may be seen that the calculation of sound power level assumes spherical

radiation of the noise from the hub of the turbine. The subtraction of 6 dB is to

determine the free ﬁeld sound pre ssure level from the measurements and to correct

for the approximate pressure doubling that occurs with the microphone located on

a reﬂecting board at ground level.

The directivity, DI, is the difference between the A-weighted sound pressure

level at measurement points i ¼ 2–4 and the reference point 1, downstream of the

turbine. It is calculated from

¼ L

Aeq,i

 L

Aeq,1

þ 20 log

(9:19)

One of the Appendices of the IEA document (International Energy Agency, 1994)

provides a method to estimate the sound pressure level of a single turbine or gro up

of turbines at a distance R provided that they are located in ﬂat and open terrain.

The calculation is based on hemispherical spreading (Equation 9.20)):

600

1 (reference measuring point)

Wind direction ⫹/⫺ 150

Figure 9.10 Recommended Pattern for Measuring Points from IEA Recommended Practices

for Wind Turbine Testing (after IEA, 1994, and BS EN 61400–11)

NOISE 535

(R) ¼ L

 10 log

(2R

)  ˜L

(9:20)

The correction ˜L

is for atmospheric absorption and can be calculated from

˜L

¼ RÆ where Æ is a coefﬁcient for sound absorption in each octave band and R

is the distance to the turbi ne hub. An alternative approach is to use a similar

equation to (9.20) but with Æ as 0:005 dB=m (as suggested in the Danish Statutory

Order on Noise from Wi ndmills, 1991) and L

speciﬁed as a single, broadband

sound power level.

If there are several wind turbines which inﬂuence the sound pressure level the

individual contributions are calculated separately and summed using

1þ2þ::

¼ 10 log

(10

=10

þ 10

=10

þ ...)(9:21)

Interestingly, the IEA Appendix concludes with the remark that in tests on small

and medium sized wind turbines (55–300 kW), the noise levels predicted in this

way were in reasonable agreement with measured noise levels (deviations of A-

weighted sound pres sure levels generally within þ=2 dB) but that serious differ-

ences were found when the prediction was based on more detailed prediction

methods.

The IEA Method (1994) for determinin g sound pressure levels at a point is based

on hemispherical spreading with a correction for atmospheric absorption. The

assumption of hemispherical spreading gives a reduction of 6 dB per doub ling of

distance. Under some conditions, particularly downwind, this may be an optimistic

assumption and a reduction of 3 dB per doubling of distance is more realistic. The

IEA Method also ignores any effects of meteorological gradients (Wagner, Bareis

and Guidati, 1996). Under normal conditions, air temperature decreases with height

and so the sound speed will decrease with increasing height and cause the path of

the sound to curve upwards. However, under conditions of temperature inversion,

e.g., as might prevail on cold winter nights, the temperature increases with height

causing the sound to curve downwards. Wind speed will have a similar effect. In

the downwind direction the sound will be bent downwards while a shadow zone is

formed upwind. The effect of the upwind shadow zone is more pronounced at

higher frequencies.

A comprehensive study of noise propagation is reported in ETSU/W/13/00385/

REP (ETSU, 2000). The results of this study, which included ﬁeld experiments,

support the concerns over the use of very complex models voiced by the IEA and

the study concluded that ‘... signiﬁcant and consistent correlation only exists

between the sound pressure level and vector wind speed’. Hence the study

proposes that a rather straightforward spherical propagation model should be

assumed with additional terms included to account for directivi ty, air absorption,

and in some cases special topographical features between the source and the

converter.

A further IEA recommendation proposes how sound pressure level measure-

ments should be taken at dwellings and other potentially sensitive locations

(International Energy Agency, 1997). It is complimentary to International Energy

Agency (1994) which provided guidance on the measurement of the source power

of a wind turbine.

536 WIND TURBINE INSTALLATIONS AND WIND FARMS

Permitted noise levels vary widely from country to co untry and even within

countries according to local planing conditions. International practice was rev iewed

by the UK ‘Working Group on Noise from Wind Turbines’, (ETSU, 1997a). In

Germany, the Netherlands and Denmark the limits are expressed in terms of a

maximum permitted value of the sound pressure level at differing locations.

In contrast, the proposal of the UK Working Group is to base the permitted noise

level of a wind farm on an increase of 5 dB(A) of the L

A90,10min

sound pressure level

above background noise. The 5 dB(A) limit was selected as being a reasonable

compromise between protecting the internal and external environment while not

unduly restricting the devel opment of wind energy itself which has other environ-

mental beneﬁts. In addition, it is suggested that a limit of less than 5 dB(A) would

be difﬁcult to monitor. BS4142 (British Standard, 1997), which is a general standard

for industrial noise and may not be directly applicable to wind farms, states that a

difference of þ10 dB or more indicates that complaints are likely while a difference

of around þ5 dB is of marginal signiﬁcance.

Applying this 5 dB(A) margin above, very quiet rural backgrounds would be too

restrictive and so ... the UK Working Group also propose a lower ﬁxed limit of 35–

40 dB(A) during daytime and 43 dB(A) during night-time. The selection of the

daytime limit of either 35 or 40 dB(A) is made by considering:

• the number of dwellings in the neighbourhood of the wind farm,

• the effect of noise limits on the number of kWh generated, and

• the duration and level of exposure.

The night-time lower limit of 43 dB(A) is derived from a 35 dB(A) sleep distur-

bance criterion, an allowance of 10 dB(A) for attenuation through an open window

and with 2 dB subtracted for the use of L

A90,10min

rather than L

Aeq,10min

. Examples of

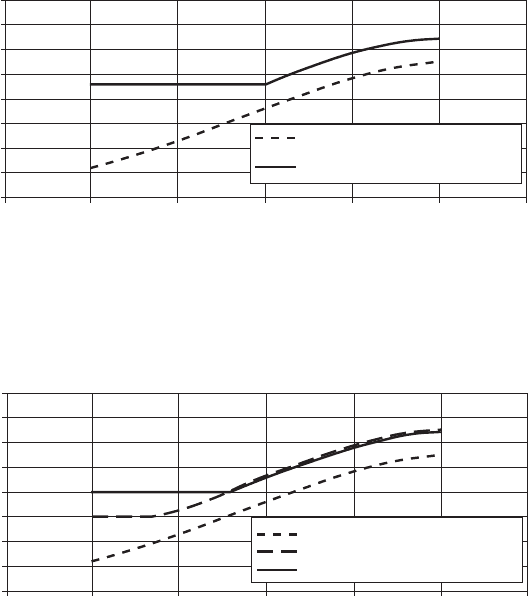
the noise criteria are shown in Figures 9.11 and 9.12. There is also a penalty for

audible tones which rises to a maximum of 5 dB.

Table 9.5 Noise Limits for Sound Pressure Levels L

Aeq

in Different

European Countries (after Gipe, 1995). Note the Deﬁnitions of Location

Vary from Country to Country; Further Details may be Found in ETSU

(1997a)

Country Commercial Mixed Residential Rural

Germany

Day

Night

Netherlands

Day

Night

Denmark 40 45

NOISE 537

9.4 Electromagnetic Interference

Wind turbines have the potential to interfere with electromagnetic signals that form

part of a wide range of modern communication systems and so their siting requires

careful assessment in respect of electromagnetic interference (EMI). In particular,

wind energy developments often compete with radio systems for hilltops and other

open sites that offer high energy outputs from wind farms and good propagation

paths for communication signals. The types of system that may be affected by EMI,

and their frequency of operation, include VHF radio systems (30–300 MHz), UHF

Television broadcasts (300 MHz–3 GHz) and microwave links (1–30 GHz). The

interaction of wind turbines with defence and civilian radar used for air trafﬁc

control has also been the subject of investigation (ETSU, 1995).

Hall (1992) reported that tests on a ﬁxed-speed 400 kW wind turbine showed that

no radio transmissions attributable to a wind turbine could be detected at 100 m.

2 4 6 8 10 12 14

Average 10 min wind speed at 10 m height: (m/s)

Sound pressure level dB(A)

Prevailing background noise level

Night-time criterion

Figure 9.11 Example of Noise Criterion Proposed by the UK Working Group on Noise from

Wind Turbines-Night-time Criterion (ETSU, 1997a) Reproduced by permission of ETSU on

behalf of DTI

2 4 6 8 10 12 14

Average 10 min wind speed at 10 m height: (m/s)

Sound pressure level dB(A)

Prevailing background noise level

35 dB criterion

40 dB criterion

Figure 9.12 Example of Noise Criterion Proposed by the UK Working Group on Noise from

Wind Turbines-Daytime Criterion (ETSU, 1997a) Reproduced by permission of ETSU on

behalf of DTI

538

WIND TURBINE INSTALLATIONS AND WIND FARMS

The electrical gene rator and associated control gear and electronics can produce

radio frequency emissions but these may be minimized by appropriate suppression

and screening at the generator. Rather than behave as an aerial the tubular tower

had a substantial screening effect on all emissions. If the nacelle is metallic this will

also screen the emissions from the nacelle itself. Although additional precautions

may be necessary with the power electronic converters of variable-speed wind

turbines, electromagnetic emission from wind turbines is not a common problem.

Scattering is, however, an important electromagnetic interference mechanism

associated with wi nd turbines. An object exposed to an electromagnetic wave

disperses incident energy in all directions and it is this spatial distribution that is

referred to as scattering.

The problem of the interaction of wind turbines and radio commun ication systems

is complex as the scattering mechanisms due to wind turbines are not readily

characterized and the signal may be modulated by the rotation of the blades. There is

also a large, and increasin g, number of types of radio systems with quite different

requirements for their effective operation. ETSU (1997b) indicates that it is expected

that the electromagnetic properties of wind turbine rotors will be inﬂuenced by:

• rotor diameter and rotational speed,

• rotor surface area, planform and blade orientation including yaw angle,

• hub height,

• structural blade materials and surface ﬁnish,

• hub construction,

• surface contamination (including rain and ice), and

• internal metal lic components including lightning protection.

The range of potential problems experienced by UK wind farms was investigated

by sending questionnaires to developers of 99 wind farms in 1996 (ETSU, 1997b).

There was one questionnaire for each operating or proposed wind farm. Of the 46

responses received, 26 projects had encountered potential problems. A summary of

the replies is given in Table 9.6. The majority of problems were associated with

potential interference with local TV reception or with TV rebroadcast links (RBL).

In the UK, where a potential problem with TV reception is identiﬁed from a

proposed wind farm, the broadcasting authorities conduct an investigation and

may then lodge an objection to the project receiving planning permission. In most

of the cases reported in the questionnaires, the objection was overcome by the

developer providing a guarantee that any loss of signal would be made good at the

expense of the wind-farm project if complaints were received. Three wind farms

reported actual local TV interference. In two cases this was rectiﬁed by modiﬁca-

tions to domestic aerials while in the other case a self-help relay transmitter was

installed and the domestic aerials realigned.

A smaller number of potential problems were reported with VHF radio and

microwave links. One project is recorded as having a broad range of problems

including:

ELECTROMAGNETIC INTERFERENCE 539

• two communications masts on the site area,

• microwave links from one mast,

• local VHF radio using both masts, including the ﬁre brigade, and

• potential interference to local TV reception and RBL.

However, after discussions with the appropriate agencies and on the basis of

detailed calculations it was possible to construct a wind farm layout that did not

lead to objections on EMI grounds.

ETSU (1997b) includes information of the practices of various radio authorities in

determining if a wind farm is likely to give rise to EMI problems. For microwave

ﬁxed links it is important that there is a clear line of sight between the transmitter

and receiver and that a proportion of the ﬁrst Fresnel zone must be free from

obstructions. The ﬁrst Fresnel zone is an ellipsoid region of space that makes the

major contribution to the signal received and within which component parts of the

signal will be in phase. At least 60 percent of the ﬁrst Fresnel zone must be free

from obstruction in order to ensure ‘free space’ propagation conditions. The radius

of the ﬁrst Fresnel zone (R

) is given by

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ºd

þ d

where d

and d

are the distance from the two microwave terminals to the point of

reference, and º is the wavelength (Figure 9.13).

In practice it is usually considered necessary to be completely outside the ﬁrst

Fresnel zone of the link with an additional exclusion zone of eithe r 200 m or 500 m

in order to avoid unwanted reﬂections. These additional allowances for reﬂections

are rather conservative rules-of-thumb and may be reduced following detailed

studies.

For UHF television relay links, if the wind farm is outside 608 of the relative

direction of the receive antenna no major problems are anticipated. If the site is

Table 9.6 Summary of Replies to Question-

naires Enquiring about Potential EMI Problems

on UK Wind-farm Projects (ETSU, 1997) (Repro-

duced by permission of ETSU on behalf of DTI)

Signal giving potential problem Number of

projects

None 20

Local TV Reception 15

TV rebroadcast link 11

Microwave link 5

Local radio 2

Civil radar 1

Defence radar 3

540

WIND TURBINE INSTALLATIONS AND WIND FARMS

within 158–608 then some problems may be anticipated but may be overcome with a

customized antenna. If the site is within 158 major problems may be anticipated.

Similar considerations apply to domestic TV reception. No problems are anticipated

if the wind farm is outside 608 of the relative direction of the domestic receive

antenna, a good quality antenna being required for 208 –608 and a new source

required if the wind farm is within 208. It is emphasized by the radio authorities

that each wind farm proposal needs to be considered individually.

9.4.1 Modelling and prediction of EMI from wind turbines

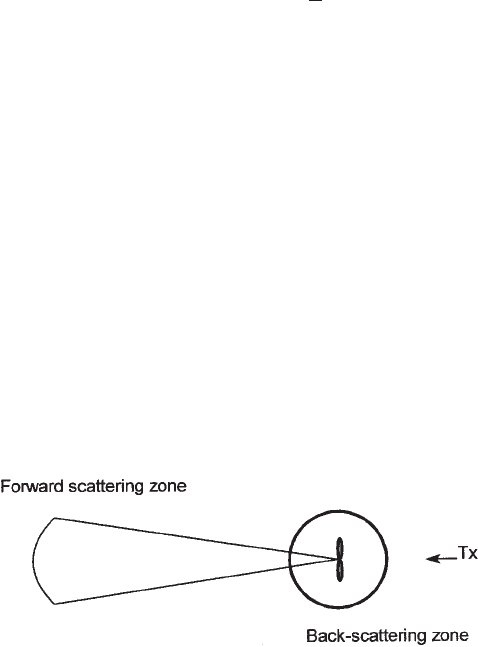
There are two fundamental interference mechanisms for EMI from wind turbines,

back-scattering and forward-scattering (Moglia, Trusszi and Orsenigo, 1996). These

are shown in Figure 9.14. Forward-scattering occurs when the wind turbine is

located between the transmitter and receiver. The interference mechanism is one of

scatter or refraction of the signal by the wind turbine and, for TV signals, it causes

fading of the picture at the rotational speed of the blades. Back-scattering occurs

when the turbine is located behind the receiver. This results in a time delay between

the wanted signal and the reﬂected interference and gives rise to ghost or double

images on a TV screen.

Moglia, Trusszi and Orsenigo (1996) (using the earlier work by van Kats and van

Receiver Transmitter

Figure 9.13 Illustration of First Fresnel Zone (Fresnel Ellipsoid)

FORWARD SCATTERING

Scattered signal

Transmitter

Direct signal

Receiver

Direct signal

Transmitter

Scattered signal

BACK SCATTERING

Figure 9.14 Interference Mechanisms of Wind Turbines with Radio Systems

ELECTROMAGNETIC INTERFERENCE 541

Rees, 1989) provide an analysis of the electromagnetic interference caused by a

wind turbine.

The useful carried signal receive d, C, is given by

C ¼ P

 A

þ G

(9:22)

where P

is the transmitter power (dB), A

is the attenuation between the

transmitter and receiver (dB), and G

is the receiver antenna gain in the direction

of the required signal (dB). The interfering signal, I, is given by

I ¼ P

 A

þ 10 log

4



 A

þ G

(9:23)

where A

is the attenuation between the transmitter and wind turbine (dB), A

is the attenuation between the wind turbine and receiver (dB), G

is the receiver

antenna gain in the direction of the reﬂected signal (dB), 10 log

(4 =º

) is the

contribution to scattering of the wind turbine (dB),  is the radar cross section (m

This may be understood as the effective area of the wind turbine. It is a function of

the wind-turbine geometry and its dielectric properties together with the signal

wavelength. º is the wavelength of the signal (m).

It may be seen that the ratio of useful signal to interference is:



¼ A

 10 log

4



þ A

 A

þ G

 G

(9:24)

Assume the distance between the transmitter and receiver is much greater than the

distance from the wind turbine to the receiver denoted as r, then A

¼ A

Assume the free space loss is A

¼ 20 log

(4r=º) and deﬁne the antenna

discrimination factor as ˜G ¼ G

 G

Then (C= I) reduces to



¼ 10 log

4 þ 20 log

r  10 log

 þ ˜G (9:25)

Thus the ratio of the useful carrier signal to interference may be improved by:

• increasing the distance from the turbine to the receiver, r,

• reducing the radar cross section, ,

• improving the discrimination factor of the antenna, ˜G.

The carrier to interference ratio (C=I) deﬁnes the quality of a radio link. For

example, a ﬁxed microwave link may have a (C=I) requirement of 50–70 dB while

for a mobile radio service the requirement may be only 15–30 dB (ETSU, 1997b).

Hence Equation (9.25) may be rearranged to deﬁne a ‘forbidden zone’ within

which a wind turbine may not be located if an adequate carrier to interference ratio

is to be maintained.

542 WIND TURBINE INSTALLATIONS AND WIND FARMS

20 log

r ¼

required

þ 10 log

  ˜G  11 (9:26)

It may be seen that the ‘forbidden zone’ is critically dependent on the radar cross

section, . Determination of the radar cross section of a wind turbine is not

straightforward and a number of approaches are described in the literature. Van

Kats and van Rees (1989) undertook a comprehensive series of site measurements

on a 45 m diameter wind turbine. They estimated a radar cross section in the back-

scatter region of 24 dBm

and a worst case value in the forward-scatter region of

46:5 dBm

(both values expressed as 10 log

 ).

Where measured results are not available, simple predictions may be made based

on approximating the turbine blades to elementary shapes (Moglia, Trusszi and

Orsenigo, 1996). For example, for a metallic cylin der the radar cross section is given

 ¼

2aL

(9:27)

where a is the radius of the cylinder (m), L is the length of the cylinder (m), and º is

the signal wavelength (m), while for a rectangular metallic plate

 ¼

4l

(9:28)

where l is the width of the plate (m).

It is suggested that, in the back-scatter region, reﬂection is only caused by the

metallic parts of the blades and so only these dimensions are used in the simple

formulae. However, in the forward-scattering region the entire blades make a

contribution although this is reduce d becau se of the blade material (GRP) and

shape. Hence, Moglia, Trusszi and Orsenigo (1996) apply the simple formulae but

with a 5 dB correction for blade material and a 10 dB correction for blade shape

(when using the rectangular appr oximation).

Hall (1992) quotes a radar cross-section model used by a number of researchers as:

10 log

 ¼ 20 log

AX(Æ)



þ 11  C (dBm

)(9:29)

where A is the area of one blade (m

), X(Æ) is a function describing the amplitude

of the scattered signal in direction Æ, º is the signal wavelength (m), C is a

calibration constant, which may be assumed to be 15 dB.

Dabis and Chignell, in ETSU (1997b), dispute the use of these simple approaches

to the determination of the radar cross section and suggest that more accurate

computation is necessary. Thei r rather complex model is based on a physical optics

formulation and assumes a conducting ﬂat plate representation of the blades. It

ignores any effects due to non-metallic blade materials and complex blade shapes.

Although Dabis and Chignell provide interesting illustrative results of their method

ELECTROMAGNETIC INTERFERENCE 543

they consider signiﬁcant further work is required to develop the technique further

and to validate it against measured ﬁeld data.

The simple approaches of Moglia, Trusszi and Orsenigo (1996) and van Kats and

van Rees (1989) allow the calculation of interference regions or forbidden zones as

indicated in Figure 9.15. The back-scattering region (for a given required (C=I)

value) has a much smaller radius than the forward-scattering region. This is

because the radar cross section is much smaller (only the metallic parts near the

root of the blades were considered) and also it is possible to take advantage of the

directivity of the receiving antenna (˜G).

Equation (9.26) deﬁnes only the radii of the two regions and it is necessary to

determine the angle over which the two regions extend. Van Kats and van Rees

(1989) remark that some uncertainty exists as to where the back-scatter region

changes into the forward-scatter region. Sengupta and Senior in Spera (1994)

suggest that 80 percent of the region around the turbine should be in the back-

scatter zone with the remaining 20 percent in the forward-scatter region. However,

Moglia, Trusszi and Orsenigo (1996) use the formula



border

¼  

(9:30)

where º is the wavelength and L the blade ele ment radius. The back-scatter region

extends between 0 , jj, 

border

, while the forward-scatter region extends be-

tween 

border

, jj, .

For the 45 m diameter turbine studied by van Kats and van Rees (1989), back-

scatter region radii of 100 m (C=I) contour of 27 dB and 200 m (C=I) contour of

33 dB were determined. The forward scattering-region was much larger with radii

of 1.3 km (C=I) contour of 27 dB and 2.7 km (C=I) contour of 33 dB. They suggest

that a (C=I) value of 33 dB should result in no visible TV interference. Moglia,

Trusszi and Orsenigo (1996) applied their method to medium-sized wind turbines

(33 m and 34 m diameter) to give a back-scatter radius of appr oximately 80 m and a

forward-scatter radius of 450 m for a 46 dB (C=I) contour. Their calculations were

supported by measured site results, which gave reasonable agreement with the

predictions. In these two examples back-scattering is unlikely to be a signiﬁcant

problem as other constraints (e.g., noise and visual effects) will ensure that the any

dwelling is outside the ‘forbidden zone’.

Figure 9.15 Example of simple calculation of interference regions of a wind turbine

544

WIND TURBINE INSTALLATIONS AND WIND FARMS