Burton T. (et. al.) Wind energy Handbook

Подождите немного. Документ загружается.

y, then Y(s) ¼ kH(s)X(s ), where X(s) and Y(s) are the Laplace transforms of x and

y. When the loop is closed at X the closed-loop dynamics can be derived as

Y9(s) ¼ kH(s)(X(s)  Y9(s )) (8:15)

where Y9(s) is the Laplace transform of the closed-loop output. This can be rewritten

Y9(s) ¼

kH(s)

1 þ kH(s)

X(s)(8:16)

In other words if the open-loop system is H(s), the closed-loop system will have

dynamics represented by H9(s) ¼ kH(s)=(1 þ kH(s)).

Now a linear transfer function can be expressed as the ratio of two polynomials

in s. Thus for the open-loop system, A(s)Y(s) ¼ B(s)X(s), and so H(s) ¼ B(s)=A(s),

where A(s) and B(s) are polynomials in s. The roots of the polynomial A(s) give

important information about the system response. Consider, for example, a ﬁrst-

order system



¼ x  y

(8:17)

representing a ﬁrst-order lagged response of y

with respect to x. This system can

be represented by the transfer function

H(s) ¼

B(s)

A(s)

(8:18)

where B(s) ¼ 1 and A(s) ¼ 1 þ s.

The single root of A(s) is given by  ¼1=, while Equation (8.17) has solutions

of the form y ¼ a þ be

 t

, with  ¼1= again. These solutions are stable if  is

positive, in other words if the root of A(s) is negative. A second-order system will

have solutions of the form y ¼ a þ be



þ ce



, where once again 

and 

are the

roots of the second-order polynomial which forms the denominat or of the transfer

function. Now 

and 

may be real numbers or they may form a complex

conjugate pair   jø. The solutions are stable if 

and 

are both negative, or if 

is negative. In general, it can be stated that a linear system is stable if all the roots of

the denominator polynomial have negative real parts. These roots are known as the

poles of the system, and they represent values of the Laplace variable which make

the transfer function inﬁnite. The roots of the numerator polynomial are known as

the zeros of the system, sin ce transfer function is zero at these points.

Now let us rewrite Equation (8.16) in terms of the polynomials A and B:

Y9(s) ¼

kB(s)

A(s) þ kB(s)

X(s)(8:19)

Clearly when the gain k is small, the closed-loop transfer function tends towards

the open-loop transfer function kB=A. However, when the gain is large the poles

CLOSED-LOOP CONTROL: ANALYTICAL DESIGN METHODS 495

will tend towards the roots of B. In other words as the gain increases from zero to

inﬁnity, the poles of the closed-loop system move from the open-loop poles and

end up at the open-loop zeros. They move along complicated trajectories in the

complex plane. A plot of these trajectories is known as a root locus plot, and is very

useful for hel ping to select the feedback gain k. The gain is selected such that all the

closed-loop poles are in the left half-plane, maki ng the system stable, and preferably

as well-damped as possible. The damping factor for a pole pair at   jø ¼ re

jŁ

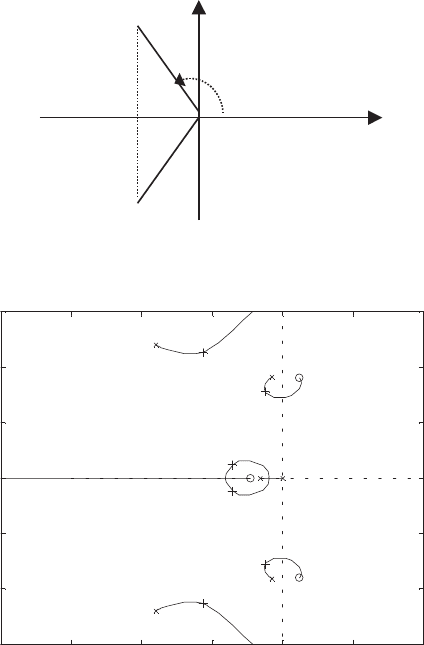
given by cos(Ł) ¼ =r, as shown in Figure 8.11.

Figure 8.12 shows an example of a root locus plot for a variable-speed pitch

controller. As the gain increases, the closed-loop poles (þ) move from the open-l oop

poles (x), corresponding to zero feedback gain, to the open-loop zeros (O). (Actually

there are usually more poles than zeros; the ‘missing’ zeros can be considered to be

equally spaced around a circle of inﬁnite radius.) In this example, the gain has been

chosen to maximize the damping of the lightly- damped tower poles (B). Any

further increase in gain would exacerbate tower vibration, eventually leading to

-4

-3 -2 -1 0 1 2-3

-2

-1

Real Axis

Imaginary Axis

Figure 8.12 Example Root Locus Plot

-σ

Figure 8.11 Damping Ratio for a Complex Pole Pair

496

THE CONTROLLER

instability as the poles cross the imaginary axis. At the chosen gain, the controller

poles (A) are well-damped. The poles at (C) result from the pitch actuator

dynamics. They remain sufﬁciently well-damped, although again, excessive gain

would drive them to instability.

Although a root locus plot is useful for helping to select the overall controller

gain, this can only be done once the other parameters deﬁning the contr oller have

been ﬁxed. A PI controller (Equ ation (8.1) with K

¼ 0) is characterized by only two

parameters, K

and K

. It can be re-written as

y ¼ K

1 þ



x (8:20)

where T

¼ K

is known as the integral time constant. The root locus plot can be

used to select K

once T

has been deﬁned, but the shape of the loci will change

with different T

. Ho wever, it is relatively straightforward to iterate on the value of

, using the root locus plot each time to select K

, until a suitable overall perform-

ance is achieved, using criteria such as those listed below. In the case of PID and

more complex controllers, wh ere more than two parameters must be selected, other

ways must be found to select the parameters, although it is always possible to use a

root locus plot for the ﬁnal choice of the overall gain.

The choice of parameters will usually be an iterative process, often using a certain

amount of trial and error, and on each iteration the performance of the resulting

controller must be assessed. Use ful measures of performance include the following.

• Gain and phase margins which are calculated from the open-loop frequency

response, and give an indication of how close the system is to instability. If the

margins are too narrow, the system may tend to become unstable. The system

will be unstable if the ope n-loop system displays a 1808 phase lag with unity gain.

The phase margin represents the difference between the actual phase lag and 1808

at the point where the open-loop gain crosses unity. A phase margin of at least

458 is usually recommended, although there is no ﬁrm rule. Similarly, the gain

margin represents the amount by which the open-loop gain is less than unity

where the open-loop phase lag crosses 1808. A gain margin of at least a few

decibels is recommended.

• The cross-over frequency, which is the frequency at which the open-loop gain

crosses unity, gives a useful measure of the responsiveness of the controller.

• The positi ons of the closed-loop poles of the system indicate how well various

resonances will be damped.

• Closed-loop step responses, for example the response of the system to a step

change in wind speed, give a useful indication of the effectiveness of the

controller. For example, in tuning a pitch controller, the rotor speed and power

excursions should return rapidly and smoothly to zero, the tower vibration

should damp out reasonably fast, and the pitch angle should change smoothly to

its new value, without too much overshoot and without too mu ch oscillation.

CLOSED-LOOP CONTROL: ANALYTICAL DESIGN METHODS 497

• Frequency responses of the closed-loop system also give some very useful

indications. For example, in the case of pitch controller:

• the frequency response from wind speed to rotor speed or electrical power

should die away at low frequencies, as the low frequency wind variations are

controlled away;

• the frequency response from wind speed to pitch angle must die away at high

frequencies, and must not be too great at critical disturbance frequencies such

as the blade-passing frequency, or the drive train resonant frequency in

variable-speed systems;

• the frequency response from wind speed to tower velocity should not have too

large a peak at the tower resonant frequency,

and so forth.

With experience it is possible, by examining measures such as these, to converge

rapidly on a controller tuning which will work well in practice.

8.4.2 Gain scheduling for pitch controllers

Close to rated, since the ﬁne pitch angle is selected to maximize power, it follows

that the sensitivity of aerodynamic torque to pitch angle is very small. Thus a much

larger controller gain is required here than at higher wind speeds, where a small

change in pitch can have a large effect on torque. Frequently the torque sensitivity

changes almos t linearly with pitch angle, and so can be compensated for by varying

the overall gain of the controller linearly in inverse proportion to the pitch angle .

Such a modiﬁcation of gain with operating point is termed a ‘gain schedule’.

However, the sensitivity of thrust to pitch angle varies in a different way, and

because of its effect on tower dynamics, which couples strongly with the pitch

controller, it may be necessary to modify the gain schedule further to ensure good

performance in all winds.

It is therfore important to generate linearized models of the system corresponding

to several different operating points between rated and cu t-out wind speed, and to

choose a gain schedule which ensures that the above performance measures are

satisfactory over the whole range.

8.4.3 Adding more terms to the controller

It is often possible to improve the per formance of a basic PI or PID controller by

adding extra terms to modify the behaviour in a particular frequency range. For

example, a pitch control algorithm may be found to cause a large amount of pitch

actuator activity at a relatively high frequency, which is of little beneﬁt in control-

ling the turbine and may be quite counter-productive. This may occur if some

498 THE CONTROLLER

dynamic mode was not taken into account in the linearized model which was used

to design the turbine. An example of this is the drive train torsional resonance in a

variable-speed turbine, which can feed through to the measured generator speed

and hence to the pitch control, causing high-frequency pitch activity which is of no

beneﬁt. Another likely cause is the pitch response to a major external forcing

frequency, such as the blade-passing frequency. While a low pass ﬁlter in series

with the controller will certainly reduce high-frequency response, the resulting

phase shift at lower frequencies may signiﬁcantly impair the overall performance of

the co ntroller. A better ‘cure’ for excessive activity at some well-deﬁned frequency

is to include a notch ﬁlter in series with the controller. A simple second-order notch

ﬁlter tuned to ﬁlter out a particular frequency of ø rad/s has a transfer function

þ ø

þ 2øs þ ø

(8:21)

where the ‘damping’ parameter  represents the width or ‘strength’ of the notch

ﬁlter. This should be increased until the ﬁltering effect is sufﬁcient at the target

frequency, without too much detriment to the control performance at lower

frequencies.

Another useful ﬁlter is the phase advance or phase lag ﬁlter,

(s þ ø

)

(s þ ø

)

(8:22)

which increases the open-loop phase lag between frequencies ø

and ø

(ø

, ø

or dec reases it if ø

. ø

. Phase advance can sometimes be useful for improving the

stability margin s. Open-loop gain and phase plots can therefore be useful for

helping to select ø

and ø

. A PID controller can be rewritten as a PI controller in

series with a phase advance (or phase lag) ﬁlter.

A general second-order ﬁlter of the form

þ 2

s þ ø

þ 2

s þ ø

(8:23)

can sometimes be useful for modifying the frequency response in a particular area.

With ø

¼ ø

and 

¼ 0 this is just a notch ﬁlter, as described above. With 

. 

the ﬁlter has a bandpass effect, which can be used to increase control action at a

particular frequency.

A root locus plot is often useful for investigating the effect of such ﬁlters. With

experience, the effect on the loci of placing the ﬁlter poles and zeros in particular

ways can be anticipated. Such techniques can help to see how, for example, a pair

of lightly-damped poles due to a structural resonance can be dragged further away

from the imaginary axis, so as to increase the damping.

CLOSED-LOOP CONTROL: ANALYTICAL DESIGN METHODS 499

8.4.4 Other extensions to classical controllers

Other extensions to classical controllers have sometimes been used in order to

further improve the performance in particular ways, for example the use of non-

linear gains, and variable or asymmetrical limits.

Non-linear gains are sometimes used to penalize large peaks or excursions in

controlled variables. For example, the gain of a PI pitch controller can be increased

as the power or speed error increases. A simple way to do this is to add to the input

signal to the PI controller a term proportional to the square or cube of the error

(remembering to adjust the sign if the square is used). This technique should be

used with caution, however, as too much non-linearity will drive the system

towards instability, in much the same way as if the linear gain is too high. This

technique requires a trial-and-error approach since it is very difﬁcult to analyse the

closed-loop behaviour of non-linear systems using standard methods. Adding the

non-linear term only when the power or speed is above the set-point will help to

reduce peaks, but will also cause a reduction in the mean power or speed, similar to

a reduction in set-point.

Asymmetrical pitch rate limits can also be used to reduce peaks. By allowing the

blades to pitch faster to wards feather than towards ﬁne, power or speed peaks will

be reduced. Once again the mean level will also be reduced by introducing this

asymmetry. However, this technique is somewhat more ‘comfortable’ than the use

of non-linear gains, in that it remains a linear system constrained by limits.

There is often a desire to reduce the set-point in high winds, to reduce the

infrequent but highly-damaging loads experienced in those conditions at the

expense of a small loss of output. It is straightforward to reduce the set-point as a

function of wind speed (the pitch angle is usually used as a measure of the rotor-

averaged wind speed, as for gain scheduling). However, the most damaging loads

occur during high turbulence, and so it would be better to reduce the set-point in

high winds only when the turbulence is also high. Rather than actually reducing

the set-point, asymmetrical rate limits provide a simple but effective means of

achieving this effect, since the rate limits will only ‘bite’ when the turbulence is

high.

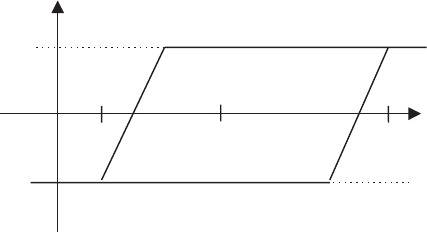
A further extension of this technique is to modify the rate limits dynamically,

even to the extent of changing the sign of a rate limit in order to force the pitc h in

one direction during certain conditions such as large power or speed excursions. A

useful application of this is in the control of variable slip systems, where it is

important to keep the speed above the minimum slip point (point B in Figure 8.8). If

the speed falls below this point, it then ceases to vary much as it is constrained by

the minimum slip curve, and so the proportional term in the PI controller ceases to

respond. Modifyi ng the rate limits as a function of speed error as in Figure 8.13 is a

useful technique to prevent this happening.

8.4.5 Optimal feedback methods

The controller design methods described above are based on classical design

techniques, and often result in relatively simple PI or PI D algorithms together with

500 THE CONTROLLER

various ﬁlters in series or in parallel, such as phase shift, notch or bandpass ﬁlters,

and sometimes using additional sensor inputs. These methods can be used to

design fairly complex high-order controllers, but only with a considerable amount

of experience on the part of the designer.

There is, however, a huge body of theory (and practice, although to a lesser

extent) relating to more advanced controller design methods, some of which have

been investigated to some extent in the context of wind-turbine control, for

example:

• self-tuning controllers,

• LQG/optimal feedback and H

control methods ,

• fuzzy logic controllers,

• neural network methods.

Self-tuning controllers (Clarke and Gaw throp, 1975) are generally ﬁxed-order

controllers deﬁned by a set of coefﬁcients, which are based on an empirical linear

model of the system. The model is used to make predictions of the sensor measure-

ments, and the prediction errors are used to update the coefﬁcients of the model

and the feedback law.

If the system dynamics are known, then some very similar mathematical theory

can be used, but applied in a different way. Rather than ﬁtting an empirical model,

a linearized physical model is used to predict sensor outputs, and the prediction

errors are used to update estimates of the system state variables. These variables

may include rotational speeds, torque s, deﬂections, etc. as well as the actual wind

speed, and so their values can be used to calculate appropriate control actions even

though those particular variables are not actuall y measured.

Observers

A subset of the known dynamics may be used to make estimates of a particular

variable: for example, some controllers use a wind-speed observer to estimate the

Sli

eed

Pitch rate

limits

Set-point,

e.g. 4% slip

1% 10%

+10 °/s

-10 °/s

Figure 8.13 Pitch Rate Limit Modiﬁcation for a Variable-slip Controller

CLOSED-LOOP CONTROL: ANALYTICAL DESIGN METHODS 501

wind speed seen by the rotor from the measured power and/or rotational speed

and the pitch angle. The estimated wind speed can then be used to deﬁne the

appropriate desired pitch angle.

State estimators

Alternatively, using a full model of the dynamics, a Kalman ﬁlter can be used to

estimate all the system states from the prediction errors (Bossanyi, 1987). This

technique can explicitly use knowledg e of the variance of any stochastic contribu-

tions to the dynamics, as well as noise on the measured signals, in a mathematically

optimum way to generate the best estimates of the states. This relies on an

assumption of Gaussian characteristics for the stochastic inputs. Thus it is possible

explicitly to take account of the stochastic nature of the wind input by formulating a

wind model driven by a Gaussian input. This can even be extended to include

blade-passing effects.

The Kalman ﬁlter can readily take account of more than one sensor input in

generating its ‘optimal’ state estimates. Thus it is ideal for making use of, for

example, an accelerometer measuring tower fore-aft motion as well as the normal

power or speed transducer. It would be straightforward to add other sensors, if

available, to improve the state estimates further.

Optimal feedback

Knowing the state estimates, it is then possible to deﬁne a cost function, which is a

function of the system state s and control actions. The controller objective can then

be deﬁned mathematically: the obje ctive is to minimize the selected cost function. If

the cost function is deﬁned as a quadratic function of the states and control actions

(which is actually a rather convenient formulation), then it is relatively straightfor-

ward to calculate the ‘optimal’ feedback law. This is deﬁned as the feedback law

which generates control signals as a linear combination of the states such that the

cost function will be minimized. Since a Linear model is required, with a Quadratic

cost function and Gaussian disturbances, this is known as an LQG controller.

This cost function approach means that the trade-off between a number of

partially competing objectives is explicitly deﬁned, by selecting suitable weights for

the terms of the cost function. This makes such a method ideal for a controller

which attempts to reduce loads as well as achieving its primary function of

regulating power or speed. Alth ough it is not practical to calculate the weightings

in the cost function rigorously, they can be adjusted in a very intuitive way. This

approach is also readily conﬁgured for multiple inputs and outputs, so for example,

as well as using generator speed and tower acceleration inputs, it can in principle

simultaneously produce the pitch demand and torque demand outputs which will

minimize the cost function.

Figure 8.14 illustrates the structure of the LQG controller, showing the state

estimator and the optimal state feedback. For implementation, the entire controller

can be reduced to a set of difference equations connecting the measured outputs ( y)

502 THE CONTROLLER

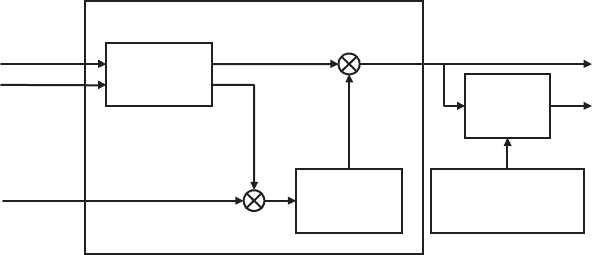
to the new control signals (u). This means that once the design is completed, the

algorithm is easy to implement and does not require massive processing power.

The linearized dynamics of the system are expressed in discrete state-space form:

x9(k) ¼ Ax(k  1) þ Bu(k  1)

The Kalman gain L is calculated taking into account the stochastic disturbances

affecting the system, and allows the state estimates to be improved by comparing

the predicted sensor outputs y9 to the actual outputs y:

x(k) ¼ x9(k) þ L( y(k  1)  y9(k  1))

where

y9(k  1) ¼ Cx(k  1) þ Du(k  1)

The optimal state feedback gain K generates the controls actions

u(k) ¼Kx(k)

where K is calculated such that the quadratic cost function J is minimized. The cost

function is

J ¼ x

Px þ u

(actually the integ ral, or the mean value over time, or the expected value of this

quantity). P and Q are the state and control weighting matrices. It is usually more

useful to deﬁne the cost function in terms of other quantities, v, which can be

considered as extra (often un-m easured) outputs of the system:

v ¼ C

x þ D

Kalman filter (state estimator)

Turbine

dynamics

x(k -1)

u(k -1)

Correction

x'(k)

x(k)

u(k)

y(k-1)

Optimal

state

feedback

y'(k-1)

Cost function

J = x

.P.x + u

.Q.u

y = measured signals y’ = predicted measurements u = control signals

x = state estimates x’ = predicted states

Figure 8.14 Structure of the LQG Controller

CLOSED-LOOP CONTROL: ANALYTICAL DESIGN METHODS 503

Hence the cost function is

J ¼ v

Rv þ u

Su ¼ x

x þ u

u þ u

so that P ¼ C

and Q ¼ D

þ S.

Another possibility is to generate optimal control signals directly as a function of

the sensor outputs. This is known as optimal output feedback (Steinbuch, 1989).

However, the mathematical solution of this problem is based on necessary condi-

tions for optimality which are not always sufﬁcient for optimality. Therefore the

solutions generated can be, and in practice often are, non-optimal and potentially

very far from optimal. This variation is therefore rather problematic.

As turbines become larger and the requirements placed on the controller become

more demanding, advanced control methods such as LQG are likely to become

increasingly used, although as yet there are few known examples of the practical

application of these techniques in commercial wind-turbines. However, this ap-

proach was used to design a controller for a 300 kW ﬁxed-speed two-bladed

teetered turbine in the UK in 1992. After testing on a prototyp e turbine in the ﬁeld,

this controller was shown to give signiﬁcant reductions in pitch activity and power

excursions compared to the original PI controller, and it was subsequently adopted

for the production machine and successfully used on over 70 turbines (Bossanyi,

2000).

LQG controllers are not necessarily robust, which means that they can be

sensitive to errors in the turbine model. A similar approach is the H

controller, in

which uncertainties in the turbine and wind mo dels can explicitly be taken into

account. Such a controller was evaluated in the ﬁeld on a 400 kW ﬁxed-speed pitch-

regulated turbine by Knudsen, Andersen and To

ffner-Clausen (1997), who reported

a reduction in pitch activity and some potential for reduced fatigue loads compared

to a PI contro ller.

8.4.6 Other methods

Rule-based or ‘fuzzy logic’ controllers are useful when the system dynamics are not

well known or when they contain important non-linearities. Control actions are

calculated by weighting the outcomes of a set of rules applied to the measured

signals. Alth ough there has been some work on fuzzy controllers for wind-turbines,

there is no clear evidence of beneﬁts. In practice, quite a good knowledge of the

system dynamics is usually available, and the dynamics can reasonably be linear-

ized at each opera ting point, so there is no clear motivation for such an approach.

The same could be said of controllers based on neural networks. These are

learning algorithms, which are ‘trained’ to generate suitable control actions using a

particular set of conditions, and then allowed to use their learnt behaviour as a

general control algorithm. While this is potentially a powerful technique, it is

difﬁcult to be sure that such a controller will generate acceptable control actions in

all circumstances.

Nevertheless, there may be some potential for such methods where signiﬁcant

non-linearities or non-stationary dynamics are involved. These might be in the

504 THE CONTROLLER