Burton T. (et. al.) Wind energy Handbook

Подождите немного. Документ загружается.

€

h þ (

€



€

)h=2(5:82)

Equation (5.81) can be integrated twice to give an expression for the displacement

at the end of the time step, which, after rearrangement yields the following expres-

sion for the corresponding acceleration:

€

( f

 f

) 

 2

€

(5:83)

Substituting Equation (5.83) into Equation (5.82) yields

( f

 f

)  2



€

h=2(5:84)

Equation (5.70) can be written as

€

þ c

þ m



(r)q

(r)dr ¼ Q

(5:85)

where the sufﬁx n refers to the state at the end of the nth time step. Substituting

Equations (5.83) and (5.84) into Equation (5.85) with n ¼ 1 and collectin g terms

yields the displacement at the end of the ﬁrst time step as:

þ m

þ 2

€



þ c

þ 2

€



(5:86)

The velocity and acceleration at the end of the ﬁrst time step are then obtained by

substituting f

in Equations (5.84) and (5.83) resp ectively.

The full procedure for obtaining the blade dynamic response to a periodic

loading using the Newm ark  ¼ 1=6 method (which is just one of many available)

may be summarized as follows:

(1) calculate the blade mode shapes, 

(r);

(2) select the number of time steps, N, per complete revolution, then the time step,

h ¼ 2=N;

(3) calculate the blade element loads, q(r, ł

) ¼ q

(r), at blade azimuth positions

corresponding to each time step (i.e., at 2=N intervals) using momentum

theory (here, the sufﬁx n denotes the number of the time step);

(4) calculate the generalized load with respect to each mode, Q



(r)q

(r)dr,

for each time step;

(5) assume initial values of blade tip displacement, velocity and acceleration;

BLADE DYNAMIC RESPONSE 265

(6) calculate ﬁrst mode blade tip displacement, velocity and acceleration at end of

ﬁrst time step, using Equations (5.86), (5.84) and (5.83) respectively (with i ¼ 1);

(7) repeat Stage 6 for each successive time step over several revolutions until

convergence achieved;

(8) calculate cyclic blade moment variation at radii of interest by multiplying the

cyclic tip displacement variation by appropriate factors derived from the modal

analysis;

(9) repeat Stages 6–8 for higher modes;

(10) combine the responses from different modes to obtain the total response.

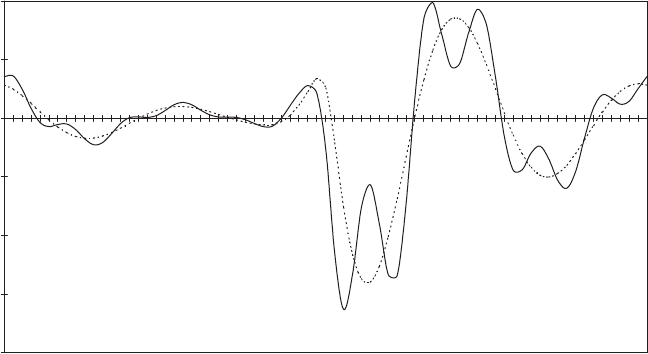
Figure 5.25 shows some results of the application of the above procedure to the

derivation of the out-of-plane root bending moment response of Blade TR to tower

shadow loading. The case chosen is for a mean wind speed of 12 m=s, uniform

across the rotor disc, and an x=D ratio of 1 (where x is the distance between the

blade and the tower centreline, and D is the tower diameter), giving a maximum

reduction in the blade root bending moment for a rigid blade of 70 kNm. Centrifu-

gal stiffening is included in the derivation of the mode shapes and frequencies, and

the damping ratios for the ﬁrst and second modes are taken as 0.17 and 0.07

respectively. It is evident from Figure 5.25 that the tower shadow gives the blade a

sharp ‘kick’ away from the tower, but the duration is too short in relation to the

duration of the ﬁrst mode half cycle for Blade TR to ‘feel’ the root bending moment

reduction that would be experienced by a completely rigid blade. The blade

-20

-15

-10

-5

360

100

110

120

130

140

150

160

170

180

190

200

210

220

230

240

250

260

270

280

290

300

310

320

330

340

350

360

Blade azimuth (Degrees)

Blade root bending moment relative to mean (kNm)

First mode

response

alone

First and second

mode

combined

response

Rotational speed = 30 r.p.m. = 0.5 Hz

First mode frequency = 1.78 Hz

Second mode frequency = 5.86 Hz

Rotor diameter = 40 m

Wind speed = 12 m/s

(uniform over disc)

Figure 5.25 Blade TR Out-of-plane Root Bending Moment Dynamic Response to Tower

Shadow

266

DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

oscillations have largely died away after a complete revo lution because of the

relatively high levels of damping.

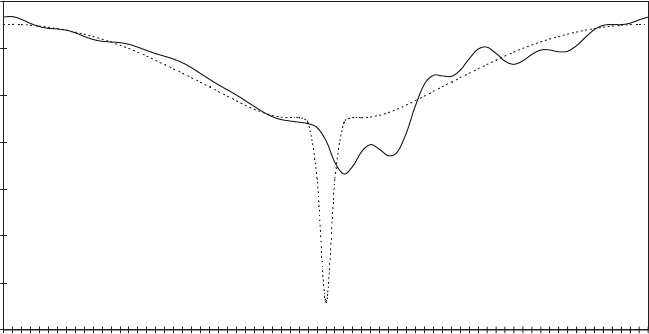
The response of the Blade TR out-of-plane root bending moment to tower shadow

combined with wind shear is shown in Figure 5.26 for a hub-height wind speed of

12 m/s. Also plotted is the corresponding bending moment for a compl etely rigid

blade. The wind shear loading is approximately sinusoidal (see Figure 5.11), and,

consequently, the response is also. However, it is worth noting that the amplitude

of the dominating ﬁrst mode response to wind shear is the result of two effects

working against each other – in other words the increase due to the dynamic

magniﬁcation factor of about 9 percent is largely cancelled out by the reduction due

to centrifugal stiffening.

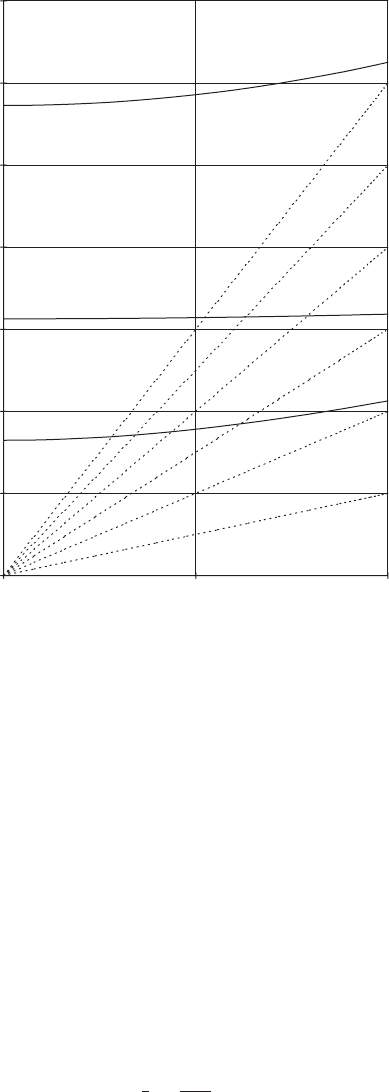
Avoidance of resonance: the Campbell diagram

In the course of blade design, it is important to avoid the occurrence of a resonant

condition, in which a blade natural frequency equates to the rotational frequency or

a harmonic with a signiﬁcant forcing load. This is often done with the aid of a

Campbell diagram, in which the blade natural frequencies are plotted out against

rotational frequency together with rays from the origin representing integer multi-

ples of the rotational frequency. Then any intersections of the rays with a blade

natural frequency over the turbine rotational speed operating range represent

possible resonances. An example of a Campbell diagram is shown in Figure 5.27.

Clearly blade periodic loading is dominated by the loading at rotational fre-

quency from wind shear, yawed ﬂow and shaft tilt (Section 5.7.2), gravity (Section

5.7.3) and gust slicing (Section 5.7.5). However, the short-lived load relief resulting

from tower shadow will be dominated by higher harmonics.

150

170

190

210

230

250

270

290

360

100

110

120

130

140

150

160

170

180

190

200

210

220

230

240

250

260

270

280

290

300

310

320

330

340

350

360

Blade azimuth

Blade root bending moment (kNm)

Root bending moment variation for

completely rigid blade

Blade TR root bending moment:

First and second mode

combined response

Rotational speed = 30 r.p.m.

Rotor diameter = 40 m

Hub-height wind speed = 12 m/s

Wind shear exponent = 0.2

Figure 5.26 Blade TR Out-of-plane Root Bending Moment Dynamic Response to Tower

Shadow and Wind Shear

BLADE DYNAMIC RESPONSE 267

5.8.6 Response to stochastic loads

The analysis of stochastic loads in the frequency domain has already been described

in Section 5.7.5 for a rigid blade, and this will now be extended to cover the

dynamic response of the different vibrati on modes of a ﬂexible blade using the

governing equation, Equation (5.70). Note that the restriction to an unstalled blade

operating at a relatively high tip speed ratio still applies.

Power spectrum of generalized blade loading

The generalized ﬂuctuating load with respect to the ith mode is Q



(r)q(r)dr,

where

q(r) ¼

r

dÆ

u(r, t)c(r)r (5:25)

03060

Rotational speed (r.p.m.)

Natural frequency (Hz)

First out-of-

plane mode

First in-plane mode

Second out-of-plane mode

Figure 5.27 Campbell Diagram for Blade TR

268

DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

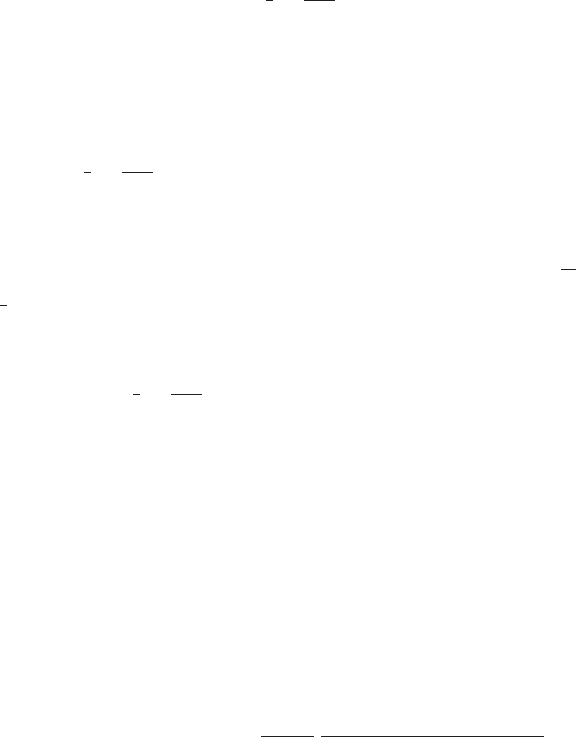
Hence

r

dÆ



(r)u(r, t)c(r)dr (5:87)

An expression for the standard deviation of Q

, 

, can be derived by a method

analagous to that given in Section A5.4 of the Appendix for a non-rotating blade,

yielding



r

dÆ



, r

, n)dn





)

)c(r

(5:88)

Here S

, r

, n) is the rotationally sampled cross spectrum for a pair of points on

the rotating blade at radii r

and r

. Equation (5.88) is parallel to Equation (A5.16) in

the Appendix with r and r9 replaced by r

and r

and (rUC

)

replaced by

(

r(dC

)=(dÆ))

. From this it can be deduced that the power spectrum of the

generalized load with respect to the ith mode is

(n) ¼

r

dÆ



, r

, n)

)

)c(r

(5:89)

In practice, this expression is evaluated using summations to approximate to the

integrals.

Power spectrum of tip deﬂection

The expression for the amplitude of the ith mode blade tip response in response to

excitation by a harmonically varying generalized load is given by Equation (A5.4)

in the Appendix. Hence the power spectrum of the tip displacement is related to

the power spectrum of the generalized load by

(n) ¼

(n)

[(1  n

)

þ 4

]

(5:90)

This can be written S

(n) ¼ (S

(n)=k

)[DMR]

where DMR stands for the dynamic

magniﬁcation ratio. n

is the ith mode natural frequency in Hz.

Figure 5.28 shows the power spectrum of ﬁrst mode tip deﬂection, S

(n), for

Blade TR operating at 30 r.p.m. in a mean wind of 8 m=s. A lower damping ratio of

0.1 has been selected so that the effect of dynamic magniﬁcation is emphasized and

the turbulence intensity has been arbitrarily set at 12.5% so that 

¼ 1m=s. Also

shown is the ﬁrst mode tip deﬂection spectrum ignoring dynamic magniﬁcation,

(n)=k

, which, when multiplied by the squa re of the dynamic magniﬁcation ratio

(also plotted), yields the S

(n) curve. The standard deviation of ﬁrst mode tip

deﬂection, 

(n)dn, comes to 54 mm, a 24 percent increase compared

with the value without dynamic magniﬁcation. The former is at a minimum,

BLADE DYNAMIC RESPONSE 269

because the blade TR ﬁrst mode natural frequency of 1.78 Hz is approximately

midway between the third and fourth harmonics of the rotational frequency. How-

ever, it is found that, even if the ﬁrst mode natural frequency coincided with the

third harmonic of the rotational frequency, 

would only increase by 4 percent.

This increase is small, because the peak of S

(n) at the third harmonic is not very

pronounced, and because the peak in the dynamic magniﬁcation ratio is relatively

broad.

Power spectrum of blade root bending moment

If the amplitude of tip deﬂection due to excitation of the blade resonant frequency

is deﬁned as x

), the amplitude of the corresponding blade root bending

moment, M

) is given by

) ¼ ø

)

m(r)

(r)r dr (5:91a)

Noting that ø

¼ k

, this becomes

)

¼ k

m(r)

(r)(r=R)dr

¼ k

R

(5:91b)

This relationship applies at all exciting frequencies, because the right-hand side is

essentially a function of mode shape. Hence the power spectrum of blade root

bending moment due to excitation of the ﬁrst mode is given by

0.1

100

1000

10000

0.01 0.1 1 10

Frequency, (Hz logarithmic scale)

(n) (logarithmic scale)

Power spectrum

of tip deflection

ignoring dynamic

magnification

(proportional to

spectrum of

generalized load)

Power

spectrum of

tip deflection

including

dynamic

magnification

Speed of rotation = 30 r.p.m. = 0.5 Hz

Mean wind speed = 8 m/s

Turbulence intensity = 12.5%

Integral length scale, L =73.5 m

First mode natural frequency = 1.78 Hz

Dynamic magnification ratio squared

based on damping ratio 0.1

Figure 5.28 Power Spectrum of Blade TR First Out-of-plane Mode Tip Deﬂection

270

DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

My1

(n) ¼ (k

R

)

(n) ¼ (R

)

(n)

[(1  n

)

þ 4

]

(5:91c)

For Blade TR, the ratio 

takes a value of 1.4.

5.8.7 Response to simulated loads

The blade dynamic response to time varying loading derived from wind simulation

(Section 5.7.6) can be obtained by a step-by-step dynam ic analysis such as that

described for use with deterministic loads in Section 5.8.5. The procedure is

essentially the same, except that it is more important to select realistic values for the

initial blade tip displacement, velocity and acceleration, unless the results from the

ﬁrst few rotation cycles are to be discarded.

5.8.8 Teeter motion

When the rotor is rigidly mounted on the shaft, out-of-plane aerodynamic loads on

the blades result in ﬂuctuating bending moments in the low speed shaft additional

to those due to gravity. In the case of two bladed machines, the transfer of blade

out-of-plane aerodynamic moments to the shaft can be eliminated and blade root

bending moments reduced by mounting the rotor on a hinge with its axis perpendi-

cular to both the low speed shaft and the axis of the rotor. This allows the rotor to

teeter to and fro in response to differential aerodynamic loads on each blade.

The restoring moment is generated by the lateral components of the centrifugal

force acting on each blade element (see Figure 5.29). It is given by

r:m(r)

r: dr ¼ I

 (5:92)

where  is the teeter angle and I is the rotor moment of inertia about its centre. The

equation of motion for free teeter oscillations is thus I

€

 þ I

 ¼ 0 (omitting the

aerodynamic damping term for the moment), indicating that the natural frequency

of the teeter motion with the teeter hinge perpendicular to the rotor axis is equal to

the rotational frequency. Since both the deterministic and stochastic components of

the exciting moment are dominated by this frequency, it is clear that the system

operates at resonance, with aerodynamic damping alone controlling the magnitude

of the teeter excursion.

The magnitude of teeter excursions would clearly be reduced if the teeter natural

frequency were moved away from the rotational frequency. This can be done by

rotating the teeter hinge axis relative to the rotor in the plane of rotation, as

illustrated in Figure 5.29, so that teeter motion results in a change of blade pitch –

positive in one blade and negative in the other – known as Delta 3 coupling.

Consider the case of blade A slicing through a gust. The increased thrust on the

blade will cause it to move in the downwind direction, by rotating about the teeter

BLADE DYNAMIC RESPONSE 271

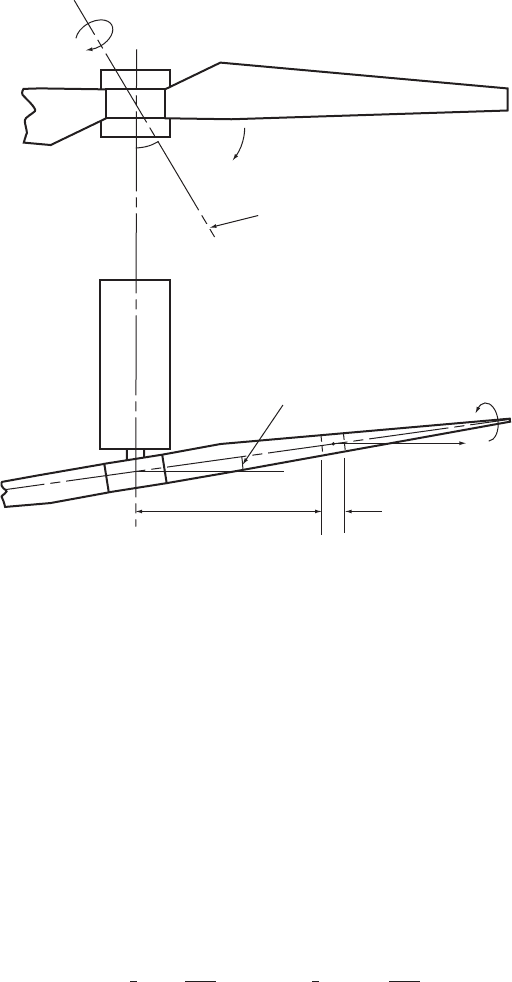
hinge. If the teeter angle, deﬁned as the rotation of the blade in its own radial plane,

is , then the increase in blade A’s pitch angle will be  tan 

, where 

is as deﬁned

in Figure 5.29. The increase in the pitch angle of blade A will reduce the angle of

attack, Æ, and thereby reduce the thr ust loading on it. The net result of this and a

simultaneous increase in the thrust loading on blade B is to introduce a restoring

moment augmenting that provided by centrifugal force.

The ﬁrst stage for the exploration of teeter response to different loadings is the

derivation of the complete equation of motion. It is assumed that the blades are

unstalled and are operating at a relatively high tip speed, so that the linear relations

adopted in the derivation of Equation (5.25) in Section 5.7.5 can be retained. The

various contributions to the change in the aerodynamic force on a blade element

relative to the steady-state situation are therefore:

rrc

dÆ

(u 

r) 

r(r)

dÆ

˜Ł (5:93)

where the three terms result from the ﬂuctuation of the incident wind, teeter motion

and Delta 3 coupling respec tively. Multiplication of these terms by radius, integra-

tion over the length of the blade and addition of the centrifugal and inertia hub

moment terms yields the following equation of motion for the teeter response:

Blade A

Teeter rotation

Axis of teeter hinge

Teeter angle ζ

Centrifugal force

Change in pitch angle

M(r)Ω

r∆r

∆β = ζ tan δ

∆r

Ω

Figure 5.29 Teeter Geometry

272

DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

€

 þ

r

dÆ

R

c(r)dr

 þ

r

dÆ

R

c(r)dr

(tan 

) þ I



r

dÆ

R

u(r, t)c(r)rjrjdr (5:94)

assuming a frozen wake. By dividing through by the moment of inertia and writing

 ¼

dÆ

R

c(r)dr

(5:95)

this can be simpliﬁed to

€

 þ 

 þ (1 þ  tan 

)

 ¼



dÆ

R

u(r, t)c(r)rjrjdr (5:96)

 is a measure of the ratio of aerodynamic to inertial forces acting on the blade, and

is one eighth of the Lock number.

Delta 3 coupling thus raises the natural frequency, ø

, of the teeter motion from

 to 

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 þ  tan 

. For a 40 m diameter rotor consisting of two TR blades

mounted on a teeter hinge set at a 

angle of 308,  ¼ 0:888 and tan 

¼ 0:577, so

the increase in natural frequency due to the 

angle is 23 percent. The correspond-

ing damping ratio, given by  ¼ (=2)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 þ  tan 

is quite high at 0.36.

Teeter response to deterministic loads

The teeter response to deterministic loads can be found usin g the same step-by-step

integration procedure set out in Section 5.8.5. However, as the loadings due to wind

shear and yaw are both approximately sinusoidal, an estimate of the max imum

teeter angle for these cases may be obtained by using the standard solution for

forced oscillations. For a harmonically varyi ng teeter moment, M

¼ M

T 0

cos t

due to wind shear, the teeter angle is given by

 ¼

Iø

cos (t  W)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

(1  (=ø

)

þ (2=ø

)

(5:97)

where W ¼ tan

1

((2=ø

)=(1  (=ø

)

)) ¼ 908  

is the phase lag with respect

to the excitation.

For the two-bladed turbine described above, rotating at 30 r.p.m. in a wind with a

hub-height mean of 12 m=s and a shear exponent of 0.2, the teeter moment

amplitude, M

, is approximately 50 kNm (see Figure 5.11, which gives the blade

root bending moment variation with azimuth for a ﬁxed hub machine, based on

momentum theory). Taking the rotor moment of inertia as 307 000 kg m

for TR

blades, and ø

¼ 1:23 rad=s, the maximum teeter angle comes to 0:98 for 

¼ 308.

This increases by about 16 percent to 1:058 if the 

angle is reduced to zero.

BLADE DYNAMIC RESPONSE 273

If the wind speed variation due to wind shear is assumed to be linear with height,

i.e., u ¼ U(kr=R), and the teeter moment is calculated from the expression on the

right-hand side of Equation (5.94), which assumes a frozen wake instead of the

equilibrium wake resulting from momentum theory, a very simple expression for

the teeter angle results in the case of zero 

angle. The teeter moment becomes

¼ M

cos t ¼

r

dÆ

R

c(r)r

dr cos  t (5:98)

Substitution of Equation (5.98) in Equation (5.97), with ø

set equal to  for the case

of a zero 

angle, results in the following expression for the teeter angle

 ¼

R

cos(t   = 2)) (5:99)

Thus the teeter response lags the excitation by 908 and the magnitude of the teeter

excursion is simply equal to the v elocity gradient divided by the rotational speed.

For a hub height of 35 m, the equivalent uniform velocity gradient over the rotor

disc for the case above is 0:125

U=R ¼ 0:075 m=s per m, giving a teeter excursion of

0.024 radians or 1:48. This differs from the earlier value of 1:05 8 because of the

frozen wake assump tion.

Teeter response to stochastic loads

As usual, it is convenient to analyse the response to the stochastic loads in the

frequency domain. The teeter moment providing excitation is given by the right-

hand side of Equation (5.94). By following a similar method to that used for the

generalized load in Section 5.8.6, the following expression for the power spectrum

of the teeter moment can be derived:

(n) ¼

r

dÆ



R

, r

, n)c(r

)c(r

jjr

jdr

(5:100)

where S

, r

, n) is the rotationally sampled cross spectrum. In practice,

, r

, n) is evaluated for a few discrete radius values, and the inte grals replaced

by summations.

The power spectrum of the teeter angle response is related to the teeter moment

power spectrum by a formula analagous to Equation (5.90), as follows:



(n) ¼

(n)

(Iø

)

[(1  2n=ø

)

þ (2:2n=ø

)

]



(5:101)

This can be written S



(n) ¼ (S

(n)=(Iø

)

)[DMR]

where DMR stands for the

dynamic magniﬁcation ratio.

Figure 5.30 shows the teeter angle power spectrum, S



(n), for a two-bladed rotor

274 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES