Будішевський В.О. Проектування транспортних систем енергоємних виробництв

Подождите немного. Документ загружается.

мальне видалення гірничих робіт. Необхідні дані можуть бути

взяті з існуючого на кожній шахті перспективного плану роз-

витку гірничих робіт.

Технологічна схема підземного транспорту, за якою транс-

портуються основний вантажопотік (вугілля) з очисних вибоїв

до скіпового стовбура, а також люди, допоміжні матеріали і

устаткування до робочих місць, складається з ряду окремих

транспортних ланок, об'єднаних між собою вузлами сполучення.

Головним визначальним фактором у загальній схемі є схема

транспорту основного вантажопотоку з очисного вибою. Вона в

значній мірі визначає схему транспорту з підготовчих вибоїв і

схему допоміжного транспорту. Схеми допоміжного транспорту

відрізняються від схем транспорту вугілля тим, що допоміжні

матеріали і устаткування доставляються в шахту стовбурами, а в

підземні − виробками спеціального призначення або вентиля-

ційними виробками.

Транспортна підземна система шахти може бути розділена

на взаємозалежні підсистеми дільничного і магістрального

транспорту.

Дільничний транспорт являє собою сукупність транспорт-

них засобів і пристроїв, розміщених у горизонтальних і похилих

виробках у межах виїмкової панелі, блоку, виїмкової ділянки,

поверху за межами видобувної виїмкової ділянки.

Магістральний транспорт являє собою сукупність транс-

портних засобів і пристроїв, розташованих у головних горизон-

тальних і капітальних похилих виробках, якими здійснюється

транспортування вантажів від виїмкових ділянок до пристовбу-

рного двору або поверхні шахти.

При тому самому просторовому розташуванні гірничих

виробок можливе застосування різних видів транспорту, отже,

на кожній шахті можна одержати безліч варіантів технологічних

схем транспорту, які будуть відрізнятися один від одного засо-

бами транспорту.

Залежно від цього найбільш характерного показника усі

технологічні схеми транспорту (основним вантажопотоком) мо-

жуть бути розділені на дві принципові групи: з одним видом

транспорту і комбіновані. У свою чергу, ці схеми мають ряд різ-

новидів, характерними представниками яких є:

− за умовою одного виду транспорту

− схема із транспор-

туванням від очисного вибою до пристовбурного двору

конвеєрами; схема транспортування від очисного вибою

до пристовбурного двору локомотивами;

− за умов комбінованого виду транспорту − схеми із

транспортуванням від очисного вибою ярусними і магі-

стральними відкаточними виробками локомотивним

відкочуванням, а похилими виробками (ухили, бремсбе-

рги) − конвеєрами; схема із транспортуванням від очис-

ного вибою ярусними відкаточними виробками конвеє-

рами з перепуском через гезенк на магістральну відка-

точну виробку з локомотивним відкочуванням.

На більшості діючих шахт у зв'язку з розмаїттям гірничо-

геологічних і гірничотехнічних умов розроблюваних родовищ

найбільш широко застосовують комбіновані схеми транспорту,

що з’єднують окремі елементи зазначених схем. Але найбільш

перспективним напрямком є повна конвеєризація транспорту

основного вантажопотоку.

Основні гірничо-геологічні і гірничотехнічні фактори, що

визначають вибір технологічних схем підземного транспорту:

кут нахилу пластів, глибина розробки, потужність, природна га-

зорясність розроблюваних пластів, розміри шахтного поля, схе-

ми і параметри розкриття, підготовки і системи розробки; поря-

док відпрацьовування шахтних полів і виїмкових ділянок, схеми

і засоби механізації, схеми провітрювання, перетину гірничих

виробок, кількість і схеми розташування очисних і підготовчих

вибоїв, викривленість гірничих виробок у профілі і плані.

Кут нахилу пласту визначає: схему розкриття; спосіб під-

готовки і систему розробки; механізацію очисних і підготовчих

робіт; навантаження на очисний вибій, концентрацію гірничих

робіт.

Потужність пласта впливає на навантаження транспортних

ланок. Зміна виробничої потужності шахти при фіксованому на-

вантаженні на лаву викликає зміну числа очисних і підготовчих

вибоїв і, отже, числа пунктів обслуговування основним і допо-

міжним транспортом.

Відстань транспортування основного і допоміжного ван-

тажопотоків прямо пропорційна розмірам шахтного поля, однак

вона залежить також від схеми розкриття, місця закладення

стовбурів, способу підготовки шахтного поля, ступеня концент-

рації робіт і ін.

Системи розробки (суцільна, стовпова, комбінована) від-

різняються інтенсивністю вантажопотоку. Великий вплив на

схеми транспорту, особливо допоміжного, і на вибір засобів для

його здійснення мають довжина лави і її добове посування, вид

механізації і кріплення лави.

Нижче розглядаються найбільш характерні, прогресивні

технологічні схеми підземного транспорту і їхніх вузлів, що від-

повідають вимогам основних напрямків техніко-економічного

розвитку галузей гірничодобувної промисловості.

На рис. 2.12 - 2.13 показані технологічні схеми дільнично-

го транспорту стосовно тих, які частіше зустрічаються у техно-

логії очисних робіт при системі розробки довгими стовпами.

Найбільш прогресивні два варіанти конвеєрних ліній:

I варіант – із застосуванням під лавою насувного переван-

тажувача і перевантаженням вугілля на звичайний стрічковий

конвеєр (рис. 2.12);

II варіант – із застосуванням телескопічного комплексу, що

складається з телескопічного конвеєра і приставного переванта-

жувача. Ці конвеєрні лінії є більше перспективними, але їхнє

застосування обмежене у виробках із хвилястим профілем (рис.

2.13).

У дільничних конвеєрних і повітряно-подавальних штре-

ках через велику хвилястість ґрунту і значних ухилах і підйомах

на окремих ділянках доставка матеріалів і устаткування до очи-

сних і підготовчих вибоїв у вагонетках за допомогою електрово-

зів не завжди можлива. У таких випадках доцільно застосовува-

ти нагрунтові канатні дороги або підвісні монорейкові дороги з

канатною або дизельною тягою.

45 м

63 м

=45 м

51 м

=45

Рисунок 2.12. Варіанти дільничних конвеєрних ліній:

−насувний скребковий перевантажувач (КСП-2 і ін.);

−стрічковий конвеєр (1Л80 і ін.); 3−приставний перевантажувач

(ПТК - 1 і ін.); 4

−стрічковий телескопічний конвеєр (1ЛТ80 і ін.)

2.4. В

ИБІР ТЕХНОЛОГІЧНОЇ СХЕМИ І ВИДІВ ТРАНСПОРТУ

Шляхи оптимізації параметрів транспортного устаткування

і технологічної схеми переміщення різних вантажів енергоємних

виробництв розглянемо в умовах складних гірничих підпри-

ємств, що здійснюють видобуток корисних копалин підземним

способом.

Корисну копалину, породу, матеріали, устаткування і лю-

дей транспортують підземними виробками шахт різними засо-

бами.

Транспортна система кожної шахти характеризується роз-

ташуванням усіх її транспортних виробок, застосовуваними в

цих виробках видами транспорту і прийнятою технологією їх-

ньої роботи, тобто технологічною схемою транспортування.

Конфігурація мережі підземних транспортних виробок, що

з'єднують очисні і підготовчі вибої зі стовбуром і поверхнею,

залежить від кількості, довжини і взаємного розташування гори-

зонтальних і похилих виробок, а також від кількості і розташу-

вання навантажувальних і обмінних пунктів.

Схема транспортних виробок шахти визначається конкрет-

ними гірничо-геологічними і гірничотехнічними умовами роз-

роблювального родовища залежно від наступних факторів: кіль-

кості одночасно розроблюваних пластів, їхнього кута падіння,

потужності і газоносності, розмірів шахтного поля, схеми роз-

криття і підготовки, системи розробки і порядку відпрацьову-

вання виїмкових полів, кількості, розташування і продуктивнос-

ті очисних і підготовчих вибоїв.

У зв'язку з розмаїттям гірничо-геологічних і гірничотехні-

чних умов вугільних родовищ схеми транспортних виробок різ-

ні. Схема виробок кожної діючої шахти має свої індивідуальні

особливості і у більшому або меншому ступені відрізняється від

схем інших шахт, що перебувають у тому самому районі. Схеми

транспортних виробок шахт, що розробляють родовища зі схо-

жими гірничо-геологічними умовами, часто мають і загальні

ознаки, що характеризують в основних рисах тип схеми. До та-

ких ознак у першу чергу ставляться: східчастість, пов'язана з на-

явністю міжгоризонтних похилих виробок, розкиданість або

компактність схеми, викликана відповідно деконцентрацією або

концентрацією гірничих робіт шахти, а також однолінійність

або розгалуженість розташування горизонтальних виробок на

основних горизонтах.

Технологічна схема підземного транспорту визначається

засобами транспорту, застосовуваними на окремих послідовних

ланках і їхніх стиках. За умов цього вибір виду транспорту для

кожної ланки залежить не тільки від гірничотехнічних умов (пи-

логазовий режим, кут нахилу виробки, розміри вантажопотоку,

довжина транспортування), але і від економічності застосування

транспортних засобів у даних умовах. Навіть за умов однакових

схем розташування виробок технологічні схеми транспортуван-

ня можуть бути різними. На тих самих горизонтальних виробках

може бути застосований конвеєрний і локомотивний транспорт,

причому в першому випадку транспорт може здійснюватися

стрічковими, пластинчастими, канатно-стрічковими і іншими

типами конвеєрів, а в другому − електровозами або дизелевоза-

ми різної зчіпної ваги, що перевозять поїзди вагонеток або сек-

ційні поїзди. При однаковому виді локомотивного транспорту

може бути застосовані різна технологія і організація його робо-

ти, наприклад одноланкове або магістрально-складальне відко-

чування, графік «наскрізного» руху або «естафетний». На тих

самих похилих виробках можуть застосовуватися або конвеєри

різних конструкцій, або канатне відкочування того або іншого

виду. Нарешті, вугілля на усіх виробках шахти або на частині їх

можна транспортувати гідравлічним способом, що дозволяє до-

ставляти корисну копалину не тільки на поверхню шахти, але і

без перевантаження безпосередньо до збагачувальної фабрики

або електростанції.

По мірі розвитку техніки будуть створюватися нові види і

засоби транспорту, які ще більше розширять можливості вибору

технологічної схеми підземного транспорту.

За умов різноманітних засобів рейкового або конвеєрного

транспорту в тих самих умовах можуть бути застосовані різні

види транспорту, близькі за продуктивністю, але нерівноцінні в

економічних відносинах. Велике значення для кожної шахти має

встановлення оптимальної технологічної схеми підземного

транспорту, що полягає у виборі таких технічних засобів для

кожної ланки транспортного ланцюга, які в сполученні забезпе-

чували б у конкретних гірничотехнічних умовах найкращі тех-

ніко-економічні показники роботи усього внутрішахтного транс-

порту.

Рекомендації, що наводяться в літературі, про області най-

більш ефективного застосування різних взаємозамінних видів

транспорту горизонтальними і похилими виробками ґрунтува-

лися на зіставленні техніко-економічних показників порівнюва-

них транспортних засобів під час роботи їх тільки в межах одні-

єї ділянки або крила, без урахування зв'язку з усією транспорт-

ною системою шахти. Такі рекомендації в найпоширеніших ви-

падках, за умов великої кількості транспортних ланок і особливо

за умов східчастого відкочування, не дають можливості визна-

чити найбільш ефективну технологічну схему підземного транс-

порту для шахти в цілому. Часто який-небудь вид транспорту,

найвигідніший на одній ділянці, на іншій аналогічній ділянці

тієї ж шахти, але у сполученні з іншими видами транспорту,

може виявитися менш економічним і навпаки. Тому для встано-

влення оптимальної технологічної схеми підземного транспорту

усієї шахти з урахуванням її особливостей не можна обмежува-

тися вибором найвигіднішого виду транспорту для кожної діля-

нки окремо, а треба розглядати транспортні засоби в їхньому

взаємозв'язку і стосовно до конкретних гірничотехнічних умов.

Комплексний розгляд усього транспортного ланцюга шах-

ти, що складається з ряду зв'язаних одна з одною ланок, вимагає

перебору і зіставлення численних технічно припустимих варіан-

тів, число яких залежить від кількості транспортних ділянок на

шахті і порівнюваних взаємозамінних видах транспорту, і різко

зростає з їхнім збільшенням.

Для розв’язання такого роду складних завдань комбіна-

торного характеру ефективно можуть бути використані мережні

методи теорії графів, що дозволяють вибрати з великої кількості

порівнюваних варіантів економічно найбільш вигідну техноло-

гічну схему підземного транспорту.

Загалом вибір оптимальної транспортної системи відпо-

відно до теорії графів, що ставляться до розв’язання завдань про

найкоротший шлях, складається із двох основних етапів:

1. Побудови моделей графів, що відображають розглянуті

конкретні транспортні схеми і види транспорту, що зі-

ставляються;

2. Виявлення оптимального розв’язання, тобто пошуки в по-

будованих графах так званого найкоротшого шляху.

При цьому застосовуються наступні вихідні дані:

1. Схема транспортних виробок шахти, стосовно до якої

вирішується завдання;

2. Види транспорту горизонтальними і похилими вироб-

ках, прийняті для зіставлення;

3. Економічні дані, що характеризують усі порівнювані

види транспорту в розглянутих конкретних умовах.

Граф можна поставити як плоске креслення, що складаєть-

ся з кінцевого числа точок, які називаються вершинами, і де-

кількох прямих або кривих відрізків (дуг), що з'єднують ті або

інші вершини.

На рис. 2.13а наведений як приклад граф, у якому є сім

вершин, позначених літерами а, б, в, г, д, е, ж і сім дуг – ад, бд,

бе, ве, ге, дж і еж.

Умовимося, що усі дуги, розглянуті далі, мають орієнта-

цію, причому в тих випадках, коли дуги спрямовані зліва напра-

во або вертикально знизу нагору, вони не позначаються стрілка-

ми, а в інших випадках їхній напрямок показується стрілкою.

Будемо називати дугу, спрямовану з вершини х у вершину

у, дугою, що виходить із вершини х і заходить у вершину у. При

цьому першу граничну точку цієї дуги х назвемо її початком, а

другу - у - її кінцем.

Шляхом у графі називається така послідовність дуг, коли

кінець кожної попередньої дуги збігається з початком наступної.

На рис. 2.13а з вершини а виходить одна дуга ад, з верши-

ни б виходять дві дуги – бд і бе і з інших вершин (крім ж) – по

одній дузі. У вершину е заходять три дуги (бе, ве, ге), а у верши-

ни д і ж по дві дуги (у першу ад і бд, а в другу дж і еж).

Тому що в графі, наведеному на рис. 2.13а, усі дуги спря-

мовані зліва направо, в ньому можна нарахувати усього 5 шля-

хів: ад, дж; бд, дж; бе, еж; ве, еж і ге, еж.

Біля кожної дуги графа написане число, яке називається

довжиною. Числа також написані і у лівих вершин графа. Тер-

мін «довжина» − умовний і може позначати як властно довжину

шляху, так і інші поняття, як, наприклад, вартість транспорту-

вання, число людино-днів і ін.

Цей граф, як і усі наступні, будується не в масштабі, тобто

розміри кожної дуги не залежать від числа, що позначає її «дов-

жину».

Кожну вершину, у яку заходять дуги, можна оцінити за мі-

німумом. Цю просту, але важливу операцію, з якою прийдеться

мати справу далі, розглянемо на наступних прикладах.

У вершину д (рис. 2.13а) заходять дві дуги: ад і бд. Для

оцінки цієї вершини за мінімуммом складемо спочатку «довжи-

ну» дуги ад із числом, написаним у вершини а, тобто 7+5, а по-

тім складемо «довжину» дуги бд із числом, написаним біля вер-

шини б, тобто 9 + 4, і із двох отриманих сум (12 і 13) виберемо

найменшу. Цю найменшу суму 12 запишемо у вершини д (рис.

2.13б) і відзначимо дугу ад, що дала нам це найменше число

(наприклад, перекреслимо її двома рисками).

У вершину е заходять три дуги: бе, ве і ге. Для оцінки цієї

вершини за мінімумом зробимо ті ж нескладні операції, як і в

попередньому випадку, тобто для кожної із цих трьох дуг скла-

демо її «довжину» і число, написане на початку дуги. З отрима-

них трьох сум (5 + 4 = 9; 8 + 3 = 11 і 10 + 4 = 14) виберемо най-

меншу — 9, запишемо її у вершини е і відзначимо двома риска-

ми дугу бе, що привела до найменшої суми (рис. 2.13б).

Рисунок 2.13. Оцінка за мінімумом вершин графа

В останню вершину ж заходять дві дуги: дж і еж. Щоб

оцінити цю вершину за мінімумом, складемо спочатку «довжи-

ну» дуги дж із числом, що ми записали біля вершини д, а потім

складемо «довжину» дуги еж із числом, що ми записали біля

вершини е. З отриманих двох сум (5 + 12 = 17 і 6 + 9 = 15) вибе-

ремо найменшу, напишемо її у вершини ж і відзначимо дугу еж

(рис. 2.13б).

На цьому і закінчується оцінка за мінімумом усіх вершин

розглянутого графа. (Для наочності на рис. 2.13б усі результати

оцінок вершин за мінімумом обведені кружками.)

Перейдемо тепер до розгляду трохи більше складного гра-

фа, наведеного на рис. 2.14а. У цьому графі є 11 вершин

(а,б,...,л) і 24 дуги (аб, ав, ... , кл). Над кожною дугою зазначена

її «довжина», а перша (початкова) вершина а позначена нулем.

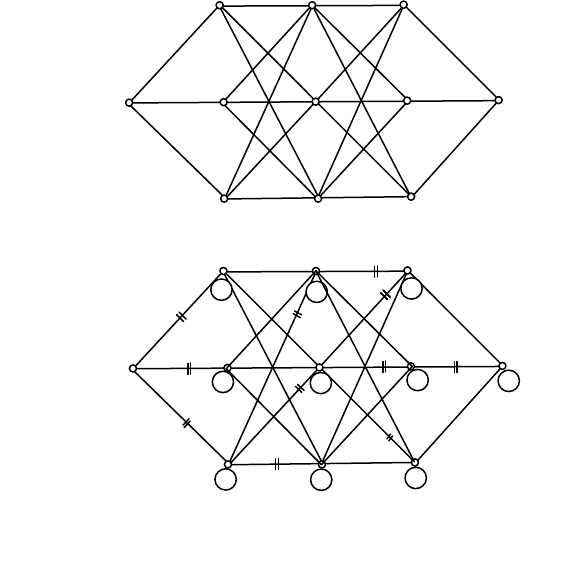
У цьому і у всіх інших аналогічних графах дуги можуть

з'єднуватися одна з іншою тільки у відповідних вершинах і ніде

більше. Тому перехрещування дуг, що виходять на кресленні, у

просторі між , не повинні розглядатися як їхнє з'єднання.

Тому що дуги графа, наведеного на рис. 2.14а, не мають

стрілок, то за прийнятої умови вони всі спрямовані зліва напра-

Рисунок 2.14. Відшукання найкоротшого шляху в графі