Бронов С.А. Исследование операций

Подождите немного. Документ загружается.

Бронов, С. А. Исследование операций: конспект лекций

B , а любую другую стратегию, и тогда компания A вообще потеряет часть

рынка или выиграет меньше, чем найденное максиминное значение.

Аналогично можно проанализировать матрицу платежей с точки зрения

компании B:

%8%9

минимакс

%8столбцов максимумы

%5%9%4%2

%8%6%6

%3%9%2%8

4321



BBBB

В данном случае приходится выбирать минимакс — формально мини-

мальную величину из максимальных (по столбцам). Таким образом, для ком-

пании B наилучшей стратегией является стратегия

B , при которой она теря-

ет лишь 5% рынка. Вообще говоря, есть такие сочетания стратегий, когда

компания B может даже выиграть 9% рынка — при сочетании стратегий

[

A ,

B ], но рассчитывать на это тоже нецелесообразно, так как при

B ком-

пания A может выбрать стратегию

A и тогда проигрыш для компании B со-

ставит уже 9%, а не 5%, как в наилучшем (наименее худшем для неё) случае.

Точка [

A ,

B ] называется седловой точкой — в ней обеспечиваются

наилучшие результаты для обоих игроков.

В рассмотренном выше примере используются точные платежи и выби-

раются однозначные стратегии — они называются чистыми стратегиями.

Если можно выбрать не одну, а несколько стратегий, то их называют сме-

шанными.

5.2 Матричные игры со смешанными стратегиями

Матричные игры — это игры, в которых присутствует матрица плате-

жей. Смешанные стратегии — это более одной стратегий, выбор которых

возможен с некоторой вероятностью. Поиск оптимальных стратегий каждого

из двух игроков ведётся с учётом вероятности выбора ими той или иной соб-

ственной стратегии. Решение можно находить методами линейного програм-

мирования или графически. Графическое решение помогает понять смысл

метода, но применимо только в случае, если один из игроков использует не

более двух стратегий (второй игрок может использовать любое количество

стратегий).

Общий принцип нахождения решения следующий. Составляется матри-

ца платежей:

Бронов, С. А. Исследование операций: конспект лекций

qqqAaa

qqqAa

,22,21,2212

,12,11,111





где играют игрок A против игрока B.

У игрока A существует лишь две возможные стратегии —

A (ею он мо-

жет воспользоваться с вероятностью

a ) и

A (ею он может воспользоваться

с вероятностью

a ). Поскольку имеется всего две стратегии, то должно вы-

полняться условие

1 aa





У игрока B существует

возможных стратегий —

B (ею он может вос-

пользоваться с вероятностью

b ),

B (ею он может воспользоваться с вероят-

ностью

b ) и т. д. вплоть до стратегии

B (ею он может воспользоваться с

вероятностью

b ). Должно выполняться условие 1





bbb



"Смешанность" стратегий означает, что игрок A в процессе игры смеши-

вает обе свои стратегии

A и

A в пропорции, заданной соответствующими

вероятностями

a и

a . Выбор конкретной стратегии осуществляется слу-

чайным образом, но из 100 выборов

100 a



раз будет выбрана стратегия

A , а

100 a



раз — стратегия

A .

Игрок B смешивает свои стратегии

B ,

B ,…,

B также случайным обра-

зом, но с соблюдением пропорций, заданных вероятностями

b ,

b ,…,

b .

В этом случае ожидаемый выигрыш игрока A, соответствующий

-ой

чистой стратегии игрока B, вычисляется следующим образом:

jjjj

qaqqW

,21,2,1

)(











Следовательно, игрок A выбирает величину

a , которая максимизирует

минимум ожидаемых выигрышей:

])[(minmax

,21,2,11

jjj

qaqqa











Данный метод рассматривается далее на простом примере.

Пример 5.2. Для игры 2×4 составлена матрица платежей игроку A игро-

ком B:

6234

1322

4321

BBBB



Бронов, С. А. Исследование операций: конспект лекций

Задача: определить пропорции, в которых должны смешивать свои стра-

тегии игроки для минимизации рисков. Ограничение вариантов одного из иг-

роков до двух позволяет графически проиллюстрировать решение задачи.

Для решения задачи составляется таблица ожидаемых выигрышей игро-

ка A в зависимости от стратегии, выбранной игроком B:

67)1(6)1()(4

2)1(23)(3

3)1(32)(2

42)1(42)(1

игрока выигрыш Ожидаемый

игрока

стратегия Чистая

1114,214,24,1

1113,213,23,1

1112,212,22,1

1111,211,21,1







aaaqaqq

Т. е. ожидаемый выигрыш представляется прямой: каждой стратегии иг-

рока B соответствует своя прямая, отражающая возможный выигрыш игрока

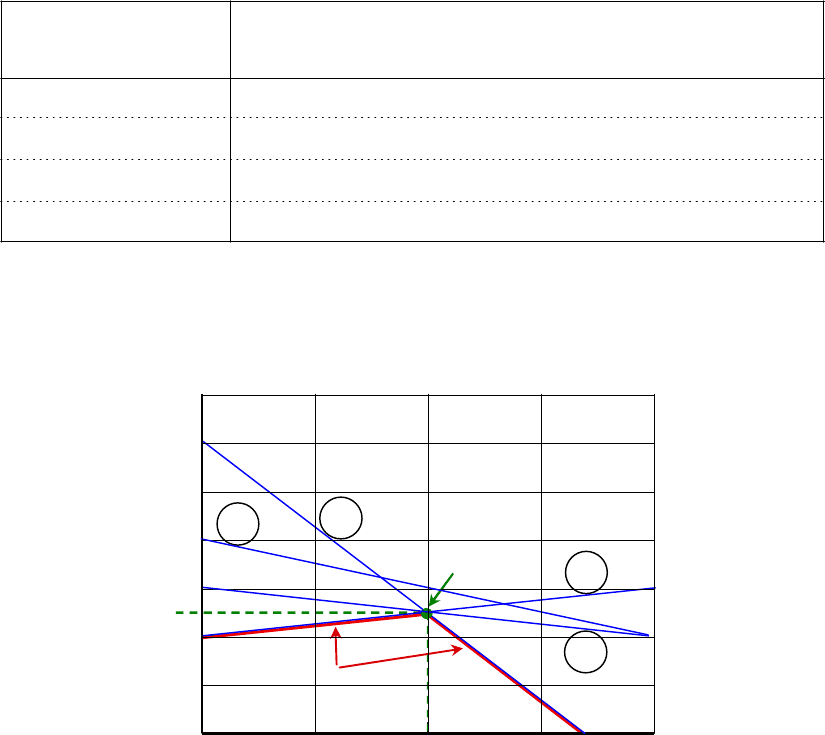
A, что может быть представлено графически (Рисунок 5.1).

Нижняя огибающая

максимин

Рисунок 5.1 — Графическое решение матричной игры двух лиц

с нулевой суммой при смешанных стратегиях (Ошибка! Источник ссылки

не найден.)

На графике (Рисунок 5.1) изображены четыре прямые линии, соответ-

ствующие четырём представленным в таблице стратегиям игрока B. Необхо-

димо определить наилучший результат из наихудших. Для этого:

1) строится нижняя огибающая, которая обеспечивает соответствующий

выигрыш игроку A, не зависимо от то стратегии, выбранной игроком B;

2) находится наивысшая точка этой огибающей (в данном случае при

5,0



a ).

Эта точка определяется пересечением прямых 3 и 4, т. е. оптимальным

решением для игрока A является смешивание стратегий

A и

A в равных

Бронов, С. А. Исследование операций: конспект лекций

долях (с 5,0



a , 5,01







aa ). В реальной игре необходимо, например,

поочерёдно менять стратегии. Выигрыш для игрока A составит в соответ-

ствии, например, с уравнением прямой 3 (или уравнение прямой 4):

5,225,02











Теперь можно оценить оптимальную стратегию игрока B. Она тоже

должна быть смешанной и зависеть от стратегий игрока B, которых две:

B и

B . Это означает, что для остальных стратегий: 0



bb и тогда

1 bb





т. е. следует искать вероятность

b (а через неё и

b ).

В этом случае ожидаемый выигрыш игрока B, соответствующий

-ой

чистой стратегии игрока A, вычисляется следующим образом:

4,34,3,

)(

kkkk

qbqqV







Следовательно, игрок B выбирает величину

b , которая максимизирует

минимум ожидаемых выигрышей:

])[(minmax

4,34,3,3

kkk

qbqqb







Для этого составляется своя таблица:

646)62()(2

14)1()]1(3[)(1

игрока выигрыш Ожидаемый

игрока

стратегия Чистая

334,234,23,2

334,134,13,1





bbqbqq

В данном случае нет необходимости делать чертёж, так как прямых все-

го две и их легко проанализировать аналитически. Необходимо найти точку

их пересечения, для чего следует их приравнять друг другу и получить урав-

нение относительно вероятности использования стратегии

B :

6414









bb , 1644







bb ,

b .

Тогда вероятность, соответствующая другой используемой стратегии —

B :

 bb .

Таким образом, наилучшим решением для игрока A является смешива-

ние его обеих стратегий

A и

A в одинаковой пропорции (1:1), а для игрока

A и

A — смешивание стратегий

B и

B , причём на каждые 8 сеансов иг-

ры следует 7 раз применять стратегию

B и 1 раз стратегию

B .

Бронов, С. А. Исследование операций: конспект лекций

Такие задачи можно решать также методами линейного программирова-

ния, особенно, если каждый игрок использует по несколько стратегий.

Бронов, С. А. Исследование операций: конспект лекций

6 Динамическое программирование

6.1 Детерминированное динамическое программирование

6.1.1 Общие принципы детерминированного динамического

программирования

Динамическое программирование предлагает способ решения много-

мерной задачи оптимизации путём декомпозиции (разбиения) её на ряд более

мелких задач — по числу переменных, по которым выполняется оптимиза-

ция. Таким образом, вместо решения одной задачи, включающей

перемен-

ных, решается

подзадач для одной переменной — своей для каждой зада-

чи. На каждом этапе общего решения могут быть свои формулировки опти-

мизационной задачи, что делает метод динамического программирования

универсальным.

Слово динамический в назывании метода присутствует потому, что ре-

шение на каждом следующем этапе опирается на решение, полученное на

предыдущем этапе. Слово программирование в назывании метода присут-

ствует потому, что его реализация выполняется в виде некоторой программы

вычислений, т. е. это не связано с программированием на алгоритмических

языках, хотя представление метода в виде компьютерной программы суще-

ственно облегчает его использование, особенно при большом числе шагов.

Вычисления в методе динамического программирования выполняются

рекуррентно, т. е. результаты решения предыдущей задачи являются исход-

ными данными для последующей. Способ вычисления рекуррентных выра-

жений зависит от конкретной задачи оптимизации (математической модели

процесса). Кроме того, для связи соседних подзадач, возможно, необходимо

учитывать одинаковые (хотя бы в некоторой части) ограничения.

Пример 6.1. Задача о кратчайшем пути.

Необходимо выбрать кратчайший путь между двумя городами при

наличии известной сети дорог (Рисунок 6.1). Начальный пункт — город в уз-

ле 1, конечный пункт — город в узле 7. Прямого пути между этими городами

нет и приходится двигаться через промежуточные узлы 2, 3, 4, 5 и 6. Каков

маршрут этого движения для обеспечения минимальной длительности?

Эту задачу можно решить путём полного перебора всех вариантов, так

как она небольшая. Но в случае большого числа промежуточных узлов зада-

ча может стать очень громоздкой и тогда следует применить специальные

методы, например, метод динамического программирования.

Для решения задачи методом динамического программирования следует

разделить её на подзадачи. В данном случае достаточно логичным представ-

ляется деление в соответствии с приведённой схемой (Рисунок 6.2).

Бронов, С. А. Исследование операций: конспект лекций

7 км

8 км

5 км

12 км

7 км

8 км

6 км

13 км

9 км

Рисунок 6.1 — Сеть дорог для задачи (Пример 6.1).

Исходные условия

7 км

12 км

8 км

13 км

9 км

8 км

5 км

7 км

17 км

12 км

5 км

7 км

0 км

8 км

5 км

6 км

9 км

17 км

12 км

21 км

7 км

8 км

Этап 1

Этап 2

Этап 3

Рисунок 6.2 — Сеть дорог для задачи о кратчайшем пути (Пример 6.1).

Разбиение на этапы

В методе динамического программирования выделяют два алгоритма:

алгоритм прямой прогонки и алгоритм обратной прогонки.

Алгоритм прямой прогонки

В алгоритме прямой прогонки движение происходит от первого узла к

последнему.

Этап 1. Исходный узел 1; последующие узлы 2, 3 и 4.

Определятся пути от исходного узла до каждого из последующих узлов:

 путь (1,2) из узла 1 до узла 2 равен 7 км;

 путь (1,3) из узла 1 до узла 3 равен 8 км;

 путь (1,4) из узла 1 до узла 4 равен 5 км.

Этап 2. Исходные узлы 2, 3 и 4; последующие узлы 5 и 6.

Бронов, С. А. Исследование операций: конспект лекций

Определяются кратчайшие пути от каждого исходного узла до каждого

последующего с учётом предыдущего пути.

Для узла 5 существует три возможных пути: (2,5), (3,5) и (4,5). К ним

нужно приплюсовать ранее найденные пути до узлов 2, 3 и 4:

 путь (1,2)+(2,5)=7+12=19 км;

 путь (1,3)+(3,5)=8+8=16 км;

 путь (1,4)+(4,5)=5+7=12 км,

из которых кратчайшим является путь (4,5)=12 км.

Для узла 6 существует два возможных пути: (3,6) и (4,6). К ним нужно

приплюсовать ранее найденные пути до узлов 3 и 4:

 путь (1,3)+(3,6)=8+9=17 км;

 путь (1,4)+(4,6)=5+13=18 км,

из которых кратчайшим является путь (3,6)=17 км.

Итоговые результаты этапа 2:

 кратчайший путь к узлу 5 равен 12 км (4,5);

 кратчайший путь к узлу 6 равен 17 км (3,6).

Этап 3. Исходные узлы 5 и 6; конечный узел 7.

Определяются кратчайшие пути от каждого исходного узла до конечно-

го с учётом предыдущего пути.

Для узла 7 существует два пути: (5,7) и (6,7). К ним нужно добавить ра-

нее определённые кратчайшие пути (4,5) до узла 5 и (3,6) до узла 6:

 путь (4,5)+(5,7)=12+9=21 км;

 путь (3,6)+(6,7)=17+6=23 км,

из которых кратчайшим является путь 21 км из узла 5.

Окончательный результат: кратчайшее расстояние (1,7) равно 21 км;

переход между узлами 1 и 7 отыскивается следующим образом: соединяются

между собой кратчайшие пути, наёденные на всех этапах:

(1,7)=(1,4)+(4,5)+(5,7)=(1)→(4)→(5)→(7)=5+7+9=21 км

Таким образом, формально при рассмотрении путей (в скобках) объеди-

няются соседние одинаковые узлы.

Обобщённая рекуррентная формула вычисления пути для алгоритма

прямой прогонки:

1i

x ,

x — узлы, между которыми определено кратчайшее расстояние на

этапе

;

)(

xf — кратчайшее расстояние до узла

x ;

),(

1 ii

xxd



— расстояние от узла

1i

x до узла

x .

Тогда )(

xf вычисляется на основе значений )(

11  ii

xf :

)}(),(min{)(

111 





iiiiii

xfxxdxf ,





Бронов, С. А. Исследование операций: конспект лекций

0)(



xf ,

где

— число этапов (подзадач); в рассмотренном примере



Алгоритм обратной прогонки

В алгоритме обратной прогонки движение происходит от последнего уз-

ла к первому.

Этап 3. Последующий (конечный) узел 7; предыдущие узлы 5 и 6.

Определяются пути от каждого предыдущего узла 5 и 6 до конечного:

 путь (5,7) из узла 5 до узла 7 равен 9 км;

 путь (6,7) из узла 6 до узла 7 равен 6 км.

Этап 2. Последующие узлы 5 и 6; предыдущие узлы 2, 3 и 4.

Определяются кратчайшие пути от каждого предыдущего узла до каж-

дого последующего с учётом последующего пути.

Для узла 5 существует три возможных пути: (2,5), (3,5) и (4,5). К ним

нужно приплюсовать ранее найденный путь до узла 7 от узла 5:

 путь (2,5)+(5,7)=12+9=21 км;

 путь (3,5)+(5,7)=8+9=17 км;

 путь (4,5)+(5,7)=7+9=16 км,

из которых кратчайшим является путь (4,5)=16 км.

Для узла 6 существует два возможных пути: (3,6) и (4,6). К ним нужно

приплюсовать ранее найденный путь до узла 7 от узла 6:

 путь (3,6)+(6,7)=9+6=15 км;

 путь (4,6)+(6,7)=13+6=19 км,

из которых кратчайшим является путь (3,6)=15 км.

Итоговые результаты этапа 2:

 кратчайший путь от узла 5 равен 16 км (4,5);

 кратчайший путь от узла 6 равен 15 км (3,6).

Этап 1. Последующие узлы 2, 3 и 4; предыдущий (начальный) узел 1.

Определяются кратчайшие пути от предыдущего узла до каждого после-

дующего с учётом кратчайшего последующего пути.

До каждого из узлов 2, 3, 4 существует лишь по одному возможному пу-

ти от узла 1: (1,2), (1,3) и (1,4). Если мы находимся в узле 5, то кратчайшим

является путь (4,5), если в узле 6, то путь (3,6). Поэтому имеется, не три, а

два варианта пути:

 путь (1,4)+(4,5)=5+16=21 км;

 путь (1,3)+(3,6)=8+15=23 км,

из которых кратчайшим является путь (1)+(4,5)=21 км.

Окончательный результат: кратчайшее расстояние (1,7) равно 21 км;

переход между узлами 1 и 7 отыскивается следующим образом: соединяются

между собой кратчайшие пути, наёденные на всех этапах:

Бронов, С. А. Исследование операций: конспект лекций

(1,7)=(1,4)+(4,5)+(5,7)=(1)→(4)→(5)→(7)=5+7+9=21 км

Таким образом, результат такой же, что и в случае алгоритма прямой

прогонки. Это естественно, так как расстояние не зависит от направления

движения: от узла 1 к узлу 7 или наоборот.

Обобщённая рекуррентная формула вычисления пути для алгоритма об-

ратной прогонки:

x ,

1i

x — узлы, между которыми определено кратчайшее расстояние на

этапе

;

)(

xf — кратчайшее расстояние до узла

x ;

),(

1ii

xxd — расстояние от узла

x до узла

1i

x .

Тогда )(

xf вычисляется на основе значений )(

11  ii

xf :

)}(),(min{)(

111 





iiiiii

xfxxdxf ,





0)(



xf ,

где

— число этапов (подзадач); в рассмотренном примере



Алгоритмы прямой и обратной прогонки эквивалентны друг другу по

получаемому результату, но не по количеству вычислений. В данном случае

в алгоритме прямой прогонки потребовалось 12 вычислений, а в алгоритме

обратной прогонки 11 вычислений (и дополнительно в обоих случаях — опе-

рации по выбору минимума по числу этапов, одинаковому для обоих алго-

ритмов). В более сложных задачах разница в количестве вычислений может

быть ещё больше. Поэтому оба алгоритма используются на практике. Оче-

видно, что в данном случае можно перенаправить направление движения (и

соответствующие стрелки) от узла 7 к узлу 1 и тогда первый алгоритм будет

формально считаться алгоритмом обратной прогонки, а второй — прямой

прогонки.

В терминах динамического программирования

x называются состоя-

ниями системы на этапе

Принцип оптимальности: на каждом этапе оптимальная стратегия

определяется независимо от стратегий, использованных на предыдущих эта-

пах.

Этот принцип называется также принципом Беллмана, впервые предло-

жившего метод динамического программирования.

При использовании метода динамического программирования выделяют

три составляющих этого метода:

1) определение этапов;

2) определение на каждом этапе вариантов решения (альтернатив);

3) определение состояний на каждом этапе.

При определении этапов приходится решать следующие задачи:

1) найти соотношения, связывающие этапы в единый процесс;