Бронов С.А. Исследование операций

Подождите немного. Документ загружается.

Бронов, С. А. Исследование операций: конспект лекций

няется ход или параметры исследуемого случайного процесса. В этом случае

можно провести последовательно серию испытаний при различных ситуаци-

ях и затем попробовать выявить закономерности процесса. Это может ока-

заться существенно проще, чем аналитически аппроксимировать составляю-

щие исследуемого процесса, так как часто такая аппроксимация требует спе-

циальных исследований и не всегда возможна.

Случайности в разных частях модели причудливо сочетаются друг с

другом, поэтому получаемая модель обычно имеет большое число возмож-

ных ветвлений. Это приводит к сравнительно простой модели сравнительно

сложного процесса, когда появляется возможность учесть самые разнообраз-

ные факторы весьма простыми средствами. Кроме случайностей, в модели

могут присутствовать и детерминированные фрагменты процесса с жёстко

заданными причинно-следственными связями.

При сложности исследуемого процесса простота его модели связана с

тем, что нет необходимости вручную специально просчитывать все возмож-

ные варианты — эту работу выполняет сама программа. В процессе счёта

фиксируются все события, величины, параметры, которые затем подвергают-

ся статистической обработке и отображаются тем или иным образом.

2.4.2 Дискретно-событийное моделирование

При имитационном моделировании процессы развиваются в функции от

некоторой независимой переменной. Вообще говоря, она может иметь раз-

личный физический смысл, но очень часто независимой переменной является

время. Во-первых, в жизни именно время является тем, что ни от чего не за-

висит, но на всё влияет. Во-вторых, многие факторы можно отразить с по-

мощью времени: например, сложность выполнения работы можно оценить

затрачиваемым на неё временем.

Процессы протекают во времени по-разному и цели их моделирования

также могут быть разными. Например, если автобус едет по маршруту, то

может казаться интересно, как меняется скорость его движения, когда он

отъезжает от остановки, подъезжает к перекрёстку, тормозит перед останов-

кой и т. д. При этом можно использовать функциональное моделирование на

основе законов механики. Это можно сделать на основе решения системы

дифференциальных уравнений, описывающих динамику механических тел

(законы Ньютона и другие физические законы), и может быть необходимо,

например, для исследования расхода горючего, износа шин и тому подобных

явлений. Если же исследуется объём перевозок, потоки пассажиров, получа-

емые доходы и т. п., то достаточно лишь самого факта и времени появления

автобуса в нужном месте, т. е. интерес представляет событие. Между сосед-

ними во времени событиями имеются временные промежутки, в которых ни-

каких событий не происходит. Следовательно, в программной модели все по-

Бронов, С. А. Исследование операций: конспект лекций

следовательные события могут протекать непосредственно друг за другом, а

время между ними определяется расчётным путём. Это можно проиллюстри-

ровать следующим образом.

При функциональном моделировании (например, при численном инте-

грировании системы дифференциальных уравнений) вначале определяется

время (начальное время

t , шаг интегрирования

, новое время tt Д



), а

затем вычисляются все переменные. При этом ось времени — равномерная

(по крайней мере, равномерным является шаг вывода).

Событие 2

Событие 3

Событие 4

Событие 1

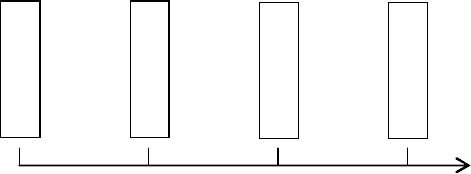
Рисунок 2.1 — Ось времени при функциональном моделировании

(промежутки времени между соседними событиями одинаковы)

При имитационном моделировании процесс привязки ко времени осу-

ществляется иначе (Рисунок 2.2):

Время или задано точно, или разыгрывается случайным образом в рам-

ках существующих условий с помощью генератора случайных чисел. Этому

времени соответствует какое-то событие. Если оно детерминированное (т. е.

происходит обязательно), то оно просто фиксируется для заданного времени

и программа переходит к следующему моменту времени, известному для

следующего события. Если событие случайное, то возможность его появле-

ния разыгрывается в этот момент времени и процесс получает новое направ-

ление развития в зависимости от результата розыгрыша.

Таким образом, при имитационном моделировании приращение времени

производится сразу — ещё до момента наступления очередного события

без промежуточных значений. Поэтому ось времени оказывается неравно-

мерной: интервал времени между первым и вторым событиями может со-

ставлять, например, 0,1 с, а между вторым и третьим, например, 1000 с.

Если в модели заранее заданы времена наступления всех событий, то эти

времена вычисляются сразу, а затем накладываются одно на другое и полу-

чается диаграмма событий во времени.

Бронов, С. А. Исследование операций: конспект лекций

Событие 2

Событие 3

1000

Событие 1

Событие 4

1002

Событие 2

Событие 3

Событие 4

Событие 1

1000

1002

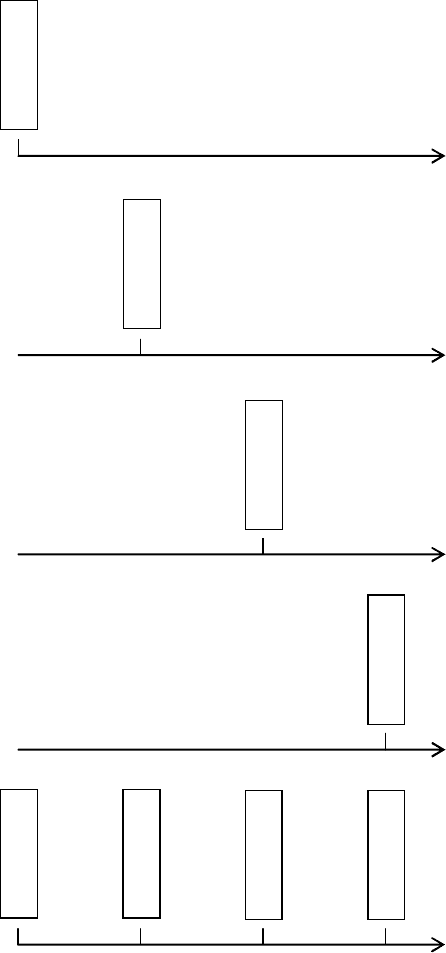
Рисунок 2.2 — Ось времени при дискретно-событийном моделировании

(промежутки времени между соседними событиями разные)

Если возможно ветвление процесса, т. е. в зависимости от условий мо-

жет происходить одно или другое событие, то программа рассчитывает вре-

мена событий до точки ветвления, затем выбирает направление развития

процесса и рассчитывает времена событий на этом направлении до следую-

щей точки возможного ветвления.

Таким образом, всегда рассчитываются только те события, которые про-

исходят, и тем самым экономится время счёта.

Бронов, С. А. Исследование операций: конспект лекций

Такое моделирование называют дискретно-событийным: дискрет-

ным — по отношению ко времени (используются времена только в точках

событий) и событийным — по отношению к характеру моделируемых эле-

ментов (ими являются именно события). При имитационном моделировании

организационных объектов используется именно дискретно-событийная

форма, которая:

во-первых, отвечает сути изучаемых процессов, главным в которых яв-

ляется последовательность событий (которые, разумеется, могут иметь свои

параметры);

во-вторых, является весьма экономичным, так как программа считает

только в точках изменения состояния модели — в моменты событий (вообще

говоря, состояние модели может и не измениться, если ожидаемое событие

не произошло из-за невыполнения каких-то условий);

в-третьих, весьма точна в отношении начала и завершения событий, так

как времена всегда рассчитываются без погрешностей.

Сами события могут иметь различную физическую природу и различное

представление в модели. Событием может быть появление в модели какого-

то объекта (например, приход посетителя), формирование сигнала времени,

совпадение каких-то условий и др.

Бронов, С. А. Исследование операций: конспект лекций

3 Метод анализа иерархий Саати

Метод анализа иерархий Томаса Саати предназначен для ранжирования,

т. е. распределения объектов в порядке их значимости по одному или не-

скольким одновременно учитываемым критериям. При этом используются

экспертные оценки значимости этих объектов.

Такую задачу можно решать разными способами. Например, эксперты

могут просто оценивать объекты в баллах (как это делается, например, в

школе или в фигурном катании или), например по 5-балльной, 20-балльной

шкалам, а затем располагать эти объекты в соответствии с присуждёнными

баллами. Недостатком этого способа является необходимость учёта взаимно-

го соотношения сразу между всеми объектами группы, что обычно затрудни-

тельно.

Наряду с указанным существует также метод парных сравнений, кото-

рым гораздо удобнее пользоваться при таких оценках. Сущность парных

сравнений заключается в том, что в группе с любым количеством объектов

(например, в группу входят объекты A, B и C) по очереди сравниваются ка-

кие-то пары объектов (например, объект A с объектом B, объект B с объектом

C, объект A с объектом C) и определяется превосходство первого по сравне-

нию со вторым по какому-либо критерию, например:

 объект A лучше объекта B в 2 раза (соответственно, объект B хуже

объекта A в 2 раза или формально — "лучше" в 1/2 раза);

 объект A лучше объекта C в 3 раза (соответственно, объект C хуже

объекта A в 3 раза или формально — "лучше" в 1/3 раза);

 объект B лучше объекта C в 5 раз (соответственно, объект C хуже объ-

екта B в 5 раз или формально — "лучше" в 1/5 раза).

Что означает "лучше", зависит от ситуации, например: привлекательнее,

функциональнее, красивее, вкуснее и т. д. — важно лишь, что при этом не-

возможно использовать количественные шкалы (метры, секунды, килограм-

мы и т. п.). Совсем другая ситуация — с ростом, временем, массой и другими

характеристиками, которые измеряются в некоторых универсальных количе-

ственных шкалах и легко сопоставляются друг с другом в соответствующих

единицах измерения.

По договорённости на первом месте всегда располагают тот объект, ко-

торый лучше. Эти результаты можно свести в таблицу (0). В такой форме

можно представлять группу, содержащую любое количество сравниваемых

объектов, так как парность сравнения связана с двухмерностью таблицы, а

не с числом объектов в группе.

Бронов, С. А. Исследование операций: конспект лекций

Таблица 3.1 — Парные сравнения между тремя объектами

A B C

2 3

1/2

1/3

1/5

Видно, что столбцы и строки таблицы принадлежат одним и тем же объ-

ектам (A, B и C). По главной диагонали этой таблицы располагается 1, так как

в соответствующих ячейках помещены сравнения объектов с самими собой

(A сравнивается с A, B сравнивается с B, C сравнивается с C). Поэтому глав-

ная диагональ любой таблицы парных сравнений всегда содержит только

единицы. В остальных ячейках размещаются симметричные относительно

главной диагонали значения: если в ячейке ниже диагонали размещено зна-

чение N, то в симметричной ей ячейке выше главной диагонали — значение

1/N. Поэтому только половина таблицы парных сравнений нуждается в за-

полнении — вторая половина заполняется автоматически. Число N обычно

выбирается в диапазоне от 1 до 10, т. е. считается, что превосходство одного

объекта над вторым более чем в 10 раз должно приводить к отбрасыванию

малозначащих объектов. Но в реальности никаких ограничений на число N

нет. При записи оценок спускаются по строкам вниз и записывают в общем

виде: X лучше Y в N раз, где X — объект по строкам, а Y — объект по столб-

цам, т. е. для определённости принято, что объект в строке лучше объекта в

столбце.

Пример 3.1. Отдел кадров подбирает для работы в фирме сотрудника из

трёх претендентов (Антонов, Воробьёв, Семёнов), пользуясь при этом одним

критерием — навыками выполнения поручаемой работы. При этом эксперты

отдела кадров затрудняются сразу ранжировать претендентов по их способ-

ностям, а разбивают их на пары и выполняют сравнения между ними внутри

каждой пары. Эти результаты можно записать в виде таблицы (0). Чтобы вы-

явить, как именно выглядит окончательное ранжирование, можно выполнить

следующие вычисления.

Прежде всего, необходимо нормировать таблицу. Для этого выполня-

ются следующие операции:

1) определяют сумму каждого столбца S:

А В С А В С

2 1/2

2 0,5

1/2

5 0,5

2 1/5

2 0,2

3,5

3,2

6,5

где в ячейках правой части таблицы значения вычисляются следующим обра-

зом:

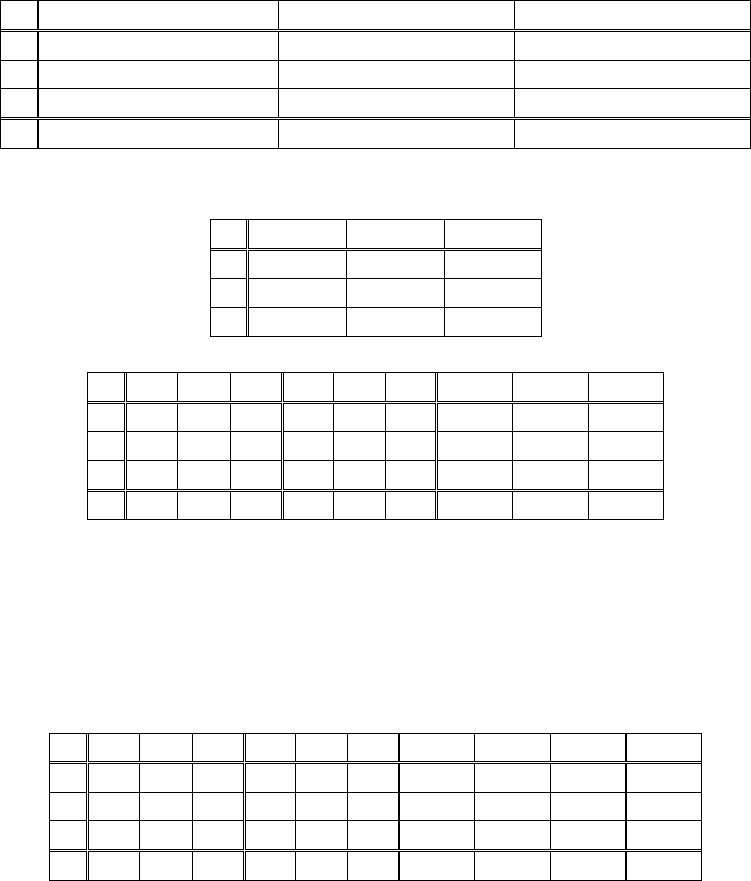
Бронов, С. А. Исследование операций: конспект лекций

А В С

A,A

=1 W

=2 W

=0,5

=0,5 W

B,B

=1 W

=2 W

=0,2 W

C,C

= W

A,A

+ W

B,A

C,A

= W

A,B

+ W

B,B

C,B

= W

A,C

+ W

B,C

C,C

2) значение в каждой ячейке пересчитывают, при этом исходное значе-

ние делят на сумму в нижней ячейке соответствующего столбца (строка S):

А В С

A,A

A,B

A,C

B,A

B,B

B,C

C,A

C,B

C,C

в результате таблица имеет вид:

А В С А В С А В С

2 1/2

2 0,5

0,286

0,625

0,077

1/2

5 0,5

5 0,143

0,313

0,769

2 1/5

2 0,2

0,571

0,063

0,154

3,5

3,2

6,5

1,000

1,001

1,000

Характерно, что сумма каждого столбца в результате оказывается равна

1 (с некоторой погрешностью округления), что и означает нормирование мат-

рицы парных сравнений.

Для окончательного ранжирования необходимо вычислить значение

окончательного весового коэффициента w каждого из объектов в каждой

строке:

А В С А В С А В С w

2 1/2

2 0,5

0,286

0,625

0,077

0,329

1/2

5 0,5

5 0,143

0,313

0,769

0,408

2 1/5

2 0,2

0,571

0,063

0,154

0,263

3,5

3,2

6,5

1,000

1,001

1,000

где окончательные весовые коэффициенты для объектов:

=(0,286+0,625+0,077)/3=0,329;

=(0,143+0,313+0,769)/3=0,408;

=(0,571+0,063+0,154)/3=0,263.

Характерным является то, что сумма последнего столбца (т. е. всех пе-

речисленных выше окончательных весовых коэффициентов) также равна 1 (с

некоторой погрешностью округления), т. е. окончательные весовые коэффи-

циенты также являются нормированными, что означает приведение их к еди-

ной шкале.

Судя по полученным значениям весовых коэффициентов, объекты сле-

дует расположить в следующем порядке: w

, w

. Т. е. наилучшим реше-

нием является выбор объекта B (Воробьёв) с наибольшим весовым коэффи-

циентом w

=0,408.

Очевидно, что при числе объектов 3 можно было бы использовать обыч-

ную оценку в баллах, но с увеличением числа объектов это будет всё более

затруднительно.

Бронов, С. А. Исследование операций: конспект лекций

Пример 3.2. Отдел кадров подбирает для работы в фирме сотрудника из

трёх претендентов (Иванов, Петров, Михайлов), пользуясь при этом тремя

критериями (собеседование, опыт работы, рекомендации), значимость кото-

рых различна; оценка значимости критериев и выбор претендента выполня-

ются методом парных сравнений.

Эксперты отдела кадров оценивают значимость критериев в соответ-

ствии с собственным опытом набора персонала (0), т. е. в их представлении:

 собеседование (С) имеет большее значение, чем опыт (О) — в данном

случае в 2 раза;

 рекомендации (Р) имеет гораздо большее значение, чем собеседование

(С) — в данном случае в 3 раза;

 опыт (О) имеет гораздо большее значение, чем рекомендации (Р) — в

данном случае в 5 раз.

В соответствии с выше изложенной процедурой выполняется нормиро-

вание матрицы парных сравнений и расчёт усреднённых весовых коэффици-

ентов.

Таблица 3.2 — Парные сравнения для сравнительной оценки критериев

выбора

С О Р С О Р С О Р w

2 1/3

2 0,333

0,222

0,625

0,053

0,300

1/2

5 0,5

5 0,111

0,313

0,790

0,405

3 1/5

3 0,2

0,667

0,063

0,158

0,296

S 4,5

3,2

6,333

1,000

1,001

Далее эксперты сравнивали между собой пары претендентов (Иванова с

Петровым, Иванова с Михайловым и Петрова с Михайловым) с использова-

нием каждого из критериев — собеседования (С), опыта работы (О) и нали-

чия рекомендаций (Р). Были получены три соответствующие таблицы пар-

ных сравнений.

Таблица 3.3 — Парные сравнения претендентов по результатам собесе-

дования

И П М И П М И П М w

4 1/2

4 0,5

0,308

0,769

0,077

0,385

1/4

5 0,25

5 0,077

0,192

0,769

0,346

2 1/5

2 0,2

0,615

0,038

0,154

0,269

S 3,25

5,2

6,5

1,000

0,999

1,000

Бронов, С. А. Исследование операций: конспект лекций

Таблица 3.4 — Парные сравнения претендентов по опыту работы

И П М И П М И П М w

2 1/4

2 0,25

0,182

0,625

0,040

0,282

1/2

5 0,5

5 0,091

0,313

0,800

0,401

4 1/5

4 0,2

0,727

0,063

0,160

0,317

S 5,5

3,2

6,25

1,000

1,001

1,000

Таблица 3.5 — Парные сравнения претендентов по рекомендациям

И П

М И П

М И П М w

3 1/3

3 0,333

0,231

0,500

0,182

0,304

1/3

1/2

0,333

0,5 0,077

0,167

0,273

0,172

3 2

0,692

0,333

0,546

0,524

S 4,333

6 1,833

1,000

1,001

1,000

В таблицах введены обозначения: И — Иванов, П — Петров, М — Ми-

хайлов; w

, w

— весовые коэффициенты для Иванова, Петрова и Михай-

лова по соответствующим критериям.

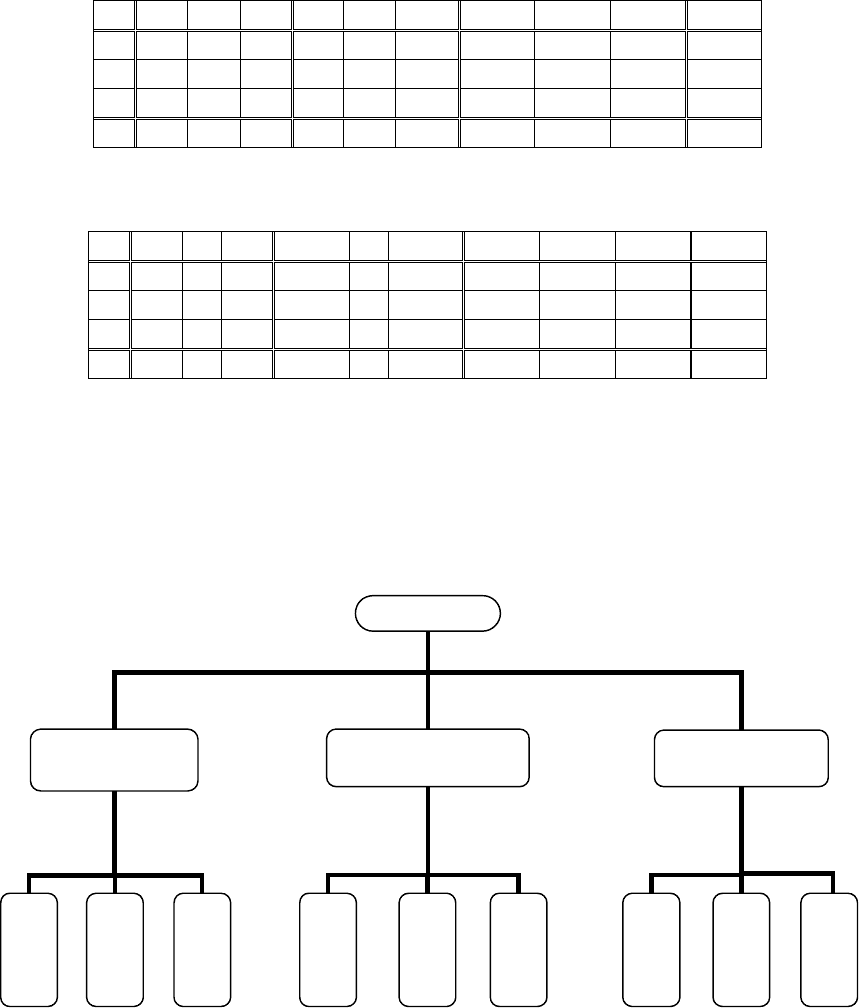
Схема расчёта по методу анализа иерархий Саати представлена ниже

(Рисунок 3.1).

Рисунок 3.1 — Схема расчёта по методу анализа иерархий Саати

Окончательный расчёт выполняется по формулам:

Иванов: (w

·w

СИ

·w

ОИ

·w

РИ

(0,300·0,385+0,405·0,282+0,296·0,304)=0,32

Петров: (w

·w

СП

·w

ОП

·w

РП

(0,300·0,346+0,405·0,401+0,296·0,172)=0,317

Михайлов: (w

·w

СМ

·w

ОМ

·w

РМ

(0,300·0,269+0,405·0,317+0,296·0,524)=0,364

Выбор

Собесе

дование

=0,300

Опыт работы

=0,405

Рекомен

дации

=0,296

Иванов

СИ

=0,385

Петров

СП

=0,346

Михайлов

СМ

=0,269

Иванов

ОИ

=0,282

Петров

ОП

=0,401

Михайлов

ОМ

=0,317

Иванов

РИ

=0,304

Петров

РП

=0,172

Михайлов

РМ

=0,524

Бронов, С. А. Исследование операций: конспект лекций

По результатам расчётов выбирается Михайлов с наивысшей оценкой

0,364.

Одна из проблем данного анализа — неточность экспертных оценок. В

связи с этим возникает необходимость оценки чувствительности решения к

этим неточностям. Эту проблему можно решать, например, следующим обра-

зом. Необходимо для каждой оценки изменить числовое значение на ±1 и пе-

ресчитать результат. Возможно, при этом ранжирование изменится. Очевид-

но, потребуется N(N−1) дополнительных вычислений. Если во всех получен-

ных результатах выбор будет один и тот же, то процедура нечувствительна к

ошибкам. Если результаты будут разными, то система чувствительна и мож-

но количественно оценить чувствительность, например, с помощью процент-

ного отношения.