Бродецкий Г.Л. Системный анализ в логистике. Выбор в условиях неопределенности

Подождите немного. Документ загружается.

201

значение с = 0,8. Кроме того, для более эффективной адаптации линий уровня такого критерия к своим

предпочтениям ЛПР для параметра γ, в отличие от предыдущей модификации производного критерия

Гурвица, выбирает значение γ= 0,4.

Шаг 1. Напомним, что соответствующая утопическая точка в поле полезностей применительно к

этой задаче имеет координаты:

= (7; 9; 6; 12).

Максимальная координата этой точки, как видим, составляет 12. Далее, как и в примере 6.1, по

формуле (*) определяем показатели

 для величин «сдвигов» по j-ой координатной оси в пространстве

доходов (для случая 100%-ой реализации таких сдвигов). Они остаются прежними:

 = 12 – 7 = 5;

 = 12 – 9 = 3;

 = 12 – 6 = 6;

 = 12 – 12 = 0.

После этого определяем показатели )(



 с учетом требований ЛПР применительно к частичной

реализации соответствующего сдвига (40% вместо 100% при указанных значениях

 ):

Показатели соответствующих сдвигов )(



 по координатным осям в пространстве доходов с

учетом требований ЛПР применительно к частичной реализации соответствующего сдвига (40% вместо

100%) будут такими:

)(



 = 0,4∙5 = 2,0; )(



 = 0,4∙3 = 1,2;

)(



 = 0,4∙6 = 2,4; )(



 = 0,4∙0 = 0.

Поэтому, реализуя процедуры модификации, вполне аналогичные тем, которые были представлены

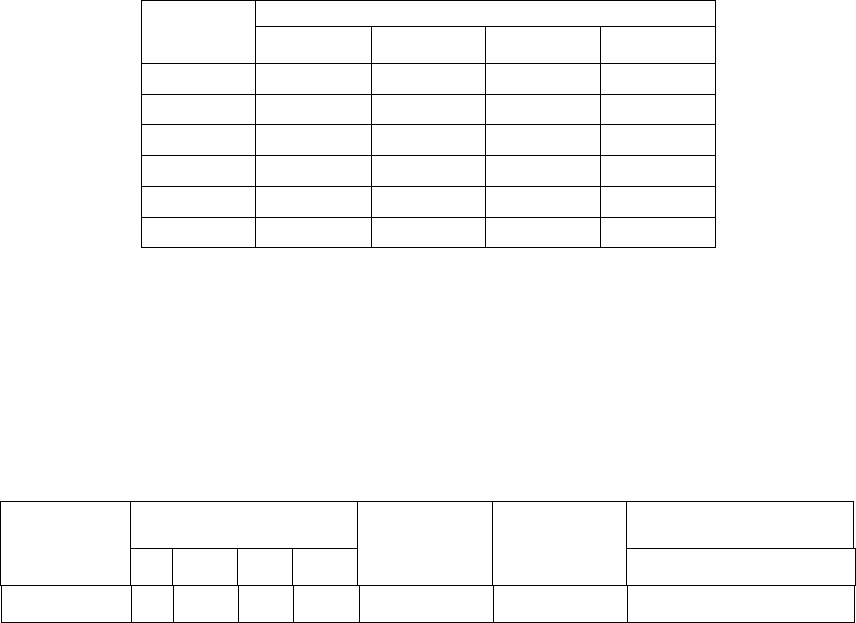
в примере 6.1, с учетом формул перехода (****), получаем следующую модифицированную матрицу

полезностей:

Доходы при событиях:

Решения



7 5,2 5,4 3

8 3,2 8,4 4

-1 7,2 4,4 12

5 10,2 3,4 5

9 2,2 7,4 3

8 7,2 3,4 4

Шаг 2. На этом шаге для указанной новой модифицированной матрицы полезностей реализуем

процедуры представленного в главе 2 традиционно используемого на практике производного HW-критерия.

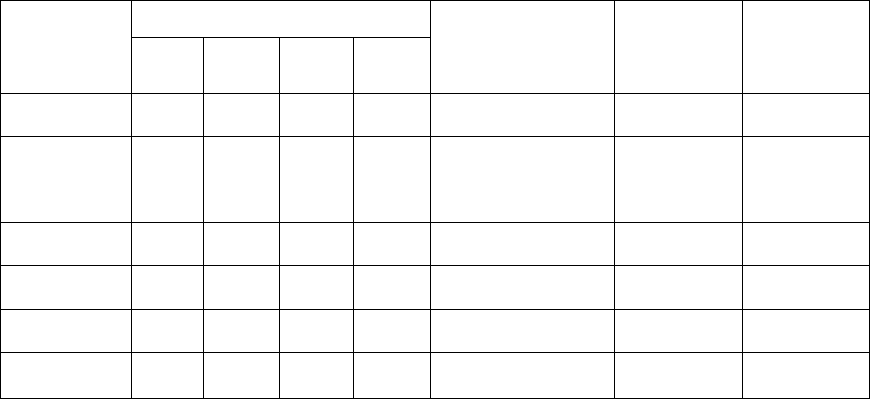
Они определяют элементы трех дополнительных столбцов, которые дописываем к этой матрице. А именно,

в первом выписаны показатели классической «крайней» пессимистической позиции (крайне осторожная

позиция) для анализируемых решений. Во втором - представлены соответствующие показатели

классической «крайней» оптимистической позиции для таких альтернатив. Наконец, в третьем столбце -

синтезированный средневзвешенный показатель критерия Гурвица с учетом заданных «весов» для

указанных крайних позиций в рамках модифицированной матрицы.

Доходы при событиях:

Синтезированный

показатель

Решения



Показатель

осторожной

позиции

Показатель

позиции

оптимизма

критерия

7 5,2 5,4 3

0.8∙3+0,2∙7 =3,8

202

8 3,2 8,4 4

3,2

8,4

0.8∙3,2+0,2∙8,4=4,24

-1 7,2 4,4 12

-1

0.8∙(-1) +0,2∙12 =1,6

5 10,2 3,4 5

3,4

10,2

0.8∙3,4+0,2∙10,2=4,76

9 2,2 7,4 3

2,2

0.8∙2,2+0,2∙9 =3,56

8 7,2 3,4 4

3,4

0.8∙3,4+0,2∙8 =4,32

Шаг 3. Находим самый большой элемент в третьем дополнительном столбце модифицированной

матрицы полезностей. Он равен 4,76 (и выделен в дополнительном столбце матрицы). Соответствующее

альтернативное решение (альтернатива X

) является оптимальным выбором по модифицированному

γ(УТ)

-критерию (при γ = 0,4 и с = 0,8).

ЗАМЕЧАНИЕ. Если сравнивать полученный здесь результат с результатом выбора по

традиционному HW-критерию (без указанной γ(УТ)-модификации, - см., в частности, аналогичную модель

примера 2.1) видим, что оптимальный выбор изменяется. А именно, здесь модифицированный HW

γ(УТ)

критерий выбрал альтернативу X

, в то время как традиционный HW-критерий при том же весовом

коэффициенте «с» будет выбирать альтернативу X

. Более того, изменилось и ранжирование анализируемых

альтернатив (по убыванию предпочтения):

, X

Это, естественно, обусловлено соответствующей модификацией, которая (при γ = 0,4) изменила линии

уровня критерия, нацелив их «частично» на утопическую току поля полезностей. Такая модификация была

реализована в соответствии с особенностями, которые были заданы ЛПР. Разумеется, снова требуется

подчеркнуть, что менеджерам необходимо понимать специфику представленной здесь модификации HW-

критерия Гурвица и уметь использовать ее, чтобы более эффективно адаптировать линии уровня критерия

применительно к системе предпочтений ЛПР.

Как и в случае предыдущей модели, проиллюстрируем теперь соответствующие возможности для

оценки приемлемых значений коэффициента γ ( ]1;0[





) в рамках рассматриваемой модификации. При

этом напомним, что возможности оценки и выбора параметра «с» (весового коэффициента для синтеза

единого показателя критерия по указанным показателям двух крайних позиций) применительно к

конкретным ЛПР в рамках критерия Гурвица уже были проиллюстрированы ранее в главе 2.

Возможность оценки и выбора параметра γ для конкретного ЛПР

при γ(УТ)-модификации в рамках критерия Гурвица

Как и для классического ММ-критерия, в этом пункте дополнительно отметим ещё одну

особенность, связанную с возможностями использования представленного HW

γ(УТ)

-критерия. А именно,

зная выбор конкретного ЛПР, который был сделан им применительно к определённой задаче принятия

решений в условиях неопределённости, и при этой модификации можно получать оценки для допустимых

значений параметра γ применительно к системе предпочтений этого ЛПР. Другими словами, можно

определять, на сколько процентов следует реализовать «сдвиг» семейства линий уровня критерия к

утопической точке поля полезностей, чтобы адаптироваться к системе предпочтений ЛПР. Такой подход

позволяет оценивать и уточнять применительно к конкретному ЛПР (по результатам известных бывших и

последующих выборов) соответствующий характер линий уровня критерия Гурвица. В частности, по

значениям указанного параметра можно интерпретировать степень склонности ЛПР к более

оптимистическим решениям (ближайшим к утопической точке поля полезностей) и степень склонности ЛПР

к осторожным классическим решениям. Для иллюстрации соответствующего подхода к оценке параметра

«γ» рассмотрим следующее дополнение к примеру 6.2.

ПРИМЕР 6.2 (Дополнение: иллюстрация процедур оценки коэффициента γ в формате

предпочтений ЛПР для критерия Гурвица). Рассмотрим упрощенную ситуацию, которая обсуждалась

выше в качестве условного примера, когда после формализации задачи принятия решений в условиях

неопределенности было выделено множество }4,1,{ j



из 4-х случайных событий. При этом,

напомним, выбиралось лучшее решение из шести альтернативных решений }6,1,{ iX

Пусть, например, в рамках этой ситуации известно, что некоторое ЛПР выбирает только именно

альтернативу X

. Оценим возможный диапазон значений для параметра γ применительно к этому ЛПР. Для

этого предварительно дополним исходную матрицу полезностей примера тремя дополнительными

столбцами, в которых представим соответствующие требуемые показатели в рамках рассматриваемой

здесь модификации. Элементы последнего третьего столбца для компактности записи представим сначала

203

только в виде обозначений для соответствующих функций переменной γ в области ]1;0[





Необходимые процедуры представлены ниже:

Доходы при событиях: Решения



Показатель

позиции

пессимизма

Показатель

позиции

оптимизма

Показатель

γ(УТ)-

критерия

5 4 3 3

3 5+2∙γ f

6 2 6 4

Min{2+3∙γ; 4} 6+2,4∙γ f

-3 6 2 12

-3 + 5∙γ 12 f

3 9 1 5

Min{1+6∙γ; 5} 9+1,2∙γ f

7 1 5 3

Min{1+3∙γ; 3} 7+2∙γ f

6 6 1 4

Min{1+6∙γ; 4} 6+2∙γ f

Для соответствующих показателей третьего столбца модифицированной матрицы полезностей

имеем (при ]1;0[





= f

(γ) = 0,8∙3 + 0,2∙(5 +2∙γ)

= f

(γ) = 0,8∙ Min{2+3∙γ; 4} + 0,2∙(6 +2,4∙γ)

= f

(γ) = 0,8∙(-3 + 5∙γ) + 0,2∙12

= f

(γ) = 0,8∙ Min{1+6∙γ; 5} + 0,2∙(9 +1,2∙γ)

= f

(γ) = 0,8∙ Min{1+3∙γ; 3} + 0,2∙(7 +2∙γ)

= f

(γ) = 0,8∙ Min{1+6∙γ; 4} + 0,2∙(6 +2∙γ)

Теперь воспользуемся тем, что согласно условию, ЛПР выбирает только именно альтернативу X

. В

контексте данного модифицированного HW

γ(УТ)

-критерия это означает, что значение показателя

составляющее 0,8∙ Min{1+6∙γ; 5} + 0,2∙(9 +1,2∙γ) (см. строку, соответствующую альтернативе X

) оказалось

самым большим (из всех показателей дополнительного столбца). Следовательно, можно выписать

соответствующую систему линейных неравенств относительно неизвестного значения γ. В веденных

обозначениях интересующая нас система неравенств имеет следующий вид:

> f

204

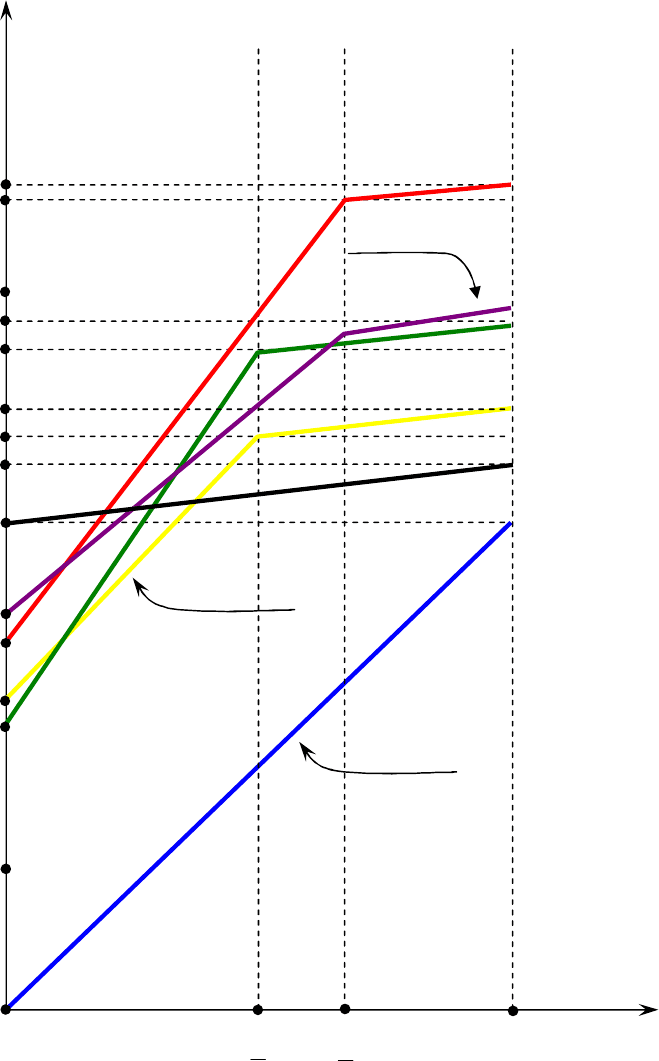
Ее решение представлено на рис. 6.6 (графическим методом). Для удобства работы с

представленными там графиками введенных выше функций f

- f

приведем дополнительно необходимые

расчеты применительно к использованным на рис. 6.6 значениям этих функций в указанных на рисунке

точках. А именно:

 для f

(0) = 0,8∙3 + 0,2∙5 = 3,4

5,96

6,04

4,8

4,6

4,2

3,8

3,4

2,8

2,6

2,2

Рис. 6.6. Показатели альтернатив для

γ(УТ)

критерия при

= 0,8

как функции f

– f

переменного γ



[0; 1].

205

(1) = 0,8∙3 + 0,2∙7 = 3,8

 для f

(0) = 0,8∙2 + 0,2∙6 = 2,8

(⅔) = 0,8∙4 + 0,2∙7,6 = 4,72

(1) = 0,8∙4 + 0,2∙8,4 =4,88

 для f

(0) = 0,8∙(-3) + 0,2∙12 = 0

(1) = 0,8∙ + 0,2∙12 = 4

 для f

(0) = 0,8∙1 + 0,2∙9 = 2,6

(⅔) = 0,8∙5 + 0,2∙9,8 = 5,96

(1) = 0,8∙5 + 0,2∙10,2 = 6,04

 для f

(0) = 0,8∙1 + 0,2∙7 = 2,2

(⅔) = 0,8∙3 + 0,2∙8,(3) = 4,0(6)

(1) = 0,8∙3 + 0,2∙9 = 4,2

 для f

(0) = 0,8∙1 + 0,2∙6 = 2

(1/2) = 0,8∙4 + 0,2∙7 = 4,6

(1) = 0,8∙4 + 0,2∙8 = 4,8

Из рис. 6.6 видно, что для решения указанной выше системы неравенств в области ]1;0[





достаточно рассмотреть решение только одного неравенства

> f

причем именно в указанной области изменения параметра γ. Поэтому решаем неравенство

0,8∙ Min{1+6∙γ; 5} + 0,2∙(9 +1,2∙γ) > 0,8∙3 + 0,2∙(5 +2∙γ).

После упрощения получаем следующее неравенство

4,4∙γ > 0,8.

Его решение дает

γ > 0,1(8).

Соответственно решение интересующей нас системы неравенств будет следующим:

]1);8(1,0(





Итак, приемлемым для такого ЛПР будет некоторое значение



из области ]1);8(1,0(





, т.к. в

рассматриваемой ситуации оптимальный выбор по модифицированному HW

γ(УТ)

-критерию будет давать

именно только альтернативу X

. Продолжая аналогичные процедуры, но уже применительно к другим

ситуациям бизнеса, естественно, можно уточнять для этого ЛПР соответствующую оценку неизвестного

коэффициента



Обратим и здесь внимание на то, что представленная модификация HW

γ(УТ)

-критерия также не

претендует на «универсальность» (как и представленная выше в этой главе модификация ММ

γ(УТ)

-критерия).

Другими словами, и здесь подчеркнем, что на практике не исключены следующие ситуации.

Альтернативное решение, которое предпочитает ЛПР, может оказаться таким, что оно не будет выбрано

модифицированным HW

γ(УТ)

-критерием ни при каком значении коэффициента ]1;0[





. Соответственно

206

для адаптации к предпочтениям такого ЛПР менеджеру понадобятся модификации, но уже применительно к

другим производным критериям принятия решений в условиях неопределенности. Проиллюстрируем это

положение применительно к рассматриваемой в этом примере ситуации.

Напомним, что в главе 2, рассматривая аналогичный пример (пример 2.2 Дополнение), было

отмечено, что ни при каком значении «весового» коэффициента С соответствующий традиционный HW-

критерий не выбирает альтернативу Х

(кстати, подчеркнем, что она не является доминируемой). Проверим,

изменится ли указанная особенность, если в такой ситуации перейти от традиционного критерия Гурвица к

его модификации на основе γ(УТ)-преобразования.

Сначала обратимся к случаю, когда после соответствующих уточнений ЛПР уже выбрало

следующее приемлемое значение коэффициента γ:

γ = 0,5.

Применительно к указанной ситуации рассмотрим следующее продолжение предыдущего примера.

Подчеркнем, что мы анализируем здесь ситуацию, когда ЛПР предпочитает именно альтернативу X

. Кроме

того, как уже подчеркивалось, нам известно, что в классе модифицированных HW

γ(УТ)

-критериев принятия

решений в условиях неопределенности соответствующее γ(УТ)-преобразование необходимо

рассматривать применительно к случаю γ = 0,5.

Пусть требуется определить, при каком значении «весового» коэффициента С (С



[0; 1])

оптимальный выбор на основе такого модифицированного HW

γ(УТ)

-критерия будет соответствовать

предпочтениям ЛПР, т.е. будет выбрана именно альтернатива X

. Поскольку анализируется γ(УТ)-

преобразование при γ = 0,5, то соответствующая модифицированная матрица полезностей будет такая же,

как и в примере 6.1. А именно:

Доходы при событиях:

Решения



7,5 5,5 6 3

8,5 3,5 9 4

-0,5 7,5 5 12

5,5 10,5 4 5

9,5 2,5 8 3

8,5 7,5 4 4

Еще раз напомним, что мы анализируем ситуацию, когда известно, что ЛПР предпочитает именно

альтернативу X

. Оценим возможный диапазон значений для «весового» показателя С применительно к

этому ЛПР в рамках модифицированного HW

γ(УТ)

-критерия. Для этого предварительно дополним матрицу

тремя столбцами. В первом представим слагаемое для показателя критерия Гурвица, обусловливаемое

учетом «крайней» пессимистической позиции. Во втором – слагаемое, обусловливаемое учетом «крайней»

оптимистической позиции. В третьем – результирующий показатель соответствующей модификации

критерия Гурвица, по наибольшему значению которого, как раз и осуществляется выбор наилучшего

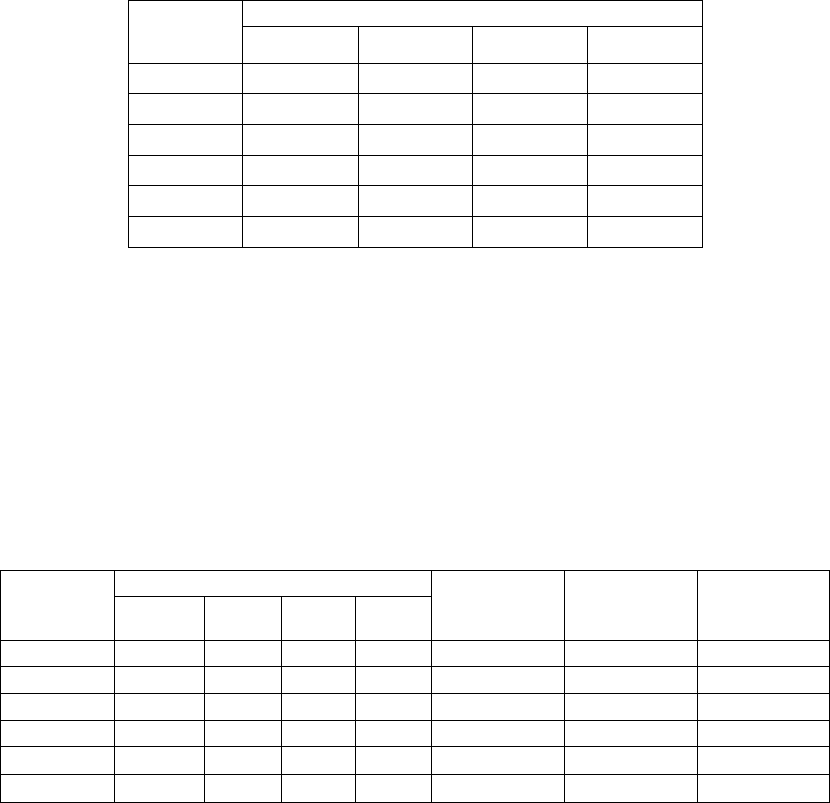
решения. Соответствующие процедуры представлены ниже. Для компактной записи элементы последнего

третьего столбца представлены как функции соответствующей переменной «с» и вынесены за пределы

таблицы:

Доходы при событиях:

Решения



Учет

позиции

пессимизма

Учет

позиции

оптимизма

Показатель

критерия

Гурвица

7,5 5,5 6 3 с∙3 (1-с)∙7,5 f

(c)

8,5 3,5 9 4 с∙3,5 (1-с)∙9 f

(c)

-0,5 7,5 5 12 с∙ (-0,5) (1-с)∙ 12 f

(c)

5,5 10,5 4 5 с∙4 (1-с)∙10,5 f

(c)

9,5 2,5 8 3 с∙2,5 (1-с)∙9,5 f

(c)

8,5 7,5 4 4 с∙4 (1-с)∙8,5 f

(c)

207

Здесь для введенных в таблице функций имеем -

Теперь воспользуемся тем, что согласно условию, ЛПР выбирает альтернативу X

. В контексте

данного критерия это означает, что показатель - 4,5∙с + 8,5 , соответствующий этой альтернативе, оказался

самым большим из всех показателей третьего дополнительного столбца. Следовательно, можно выписать

следующую систему линейных неравенств относительно неизвестного значения интересующего ЛПР

параметра с:

- 4,5∙с + 8,5 > - 4,5∙с + 7,5

- 4,5∙с + 8,5 > - 5,5∙с + 9

- 4,5∙с + 8,5 > - 12,5∙с + 12

- 4,5∙с + 8,5 > - 6,5∙с + 10,5

- 4,5∙с + 8,5 > - 7∙с + 9,5

Предпоследнее неравенство после элементарного упрощения имеет вид с > 1. Следовательно в

области с



[0; 1] интересующая нас система неравенств не имеет решения. Итак, как видим, в рамках

анализируемой ситуации при γ = 0,5 соответствующее γ(УТ)-преобразование не помогает адаптировать

линии уровня критерия Гурвица таким образом, чтобы соответствовать предпочтениям ЛПР (чтобы

выбирать альтернативу X

в качестве оптимальной).

Однако, тем не менее, может быть такому ЛПР (предпочитающему именно альтернативу X

рамках рассматриваемого примера) следует искать приемлемое γ(УТ)-преобразование линий уровня

критерия Гурвица при других значениях коэффициента γ? Покажем, что в нашем примере указанное

требование не будет выполнено, ни при каких значениях коэффициента γ из области значений γ



[0; 1].

Для этого нам, в частности, будет достаточно доказать, что при любом γ



[0; 1] и любом С



[0; 1]

альтернатива X

будет иметь такой показатель соответствующего модифицированного критерия, который

будет меньшим, чем показатель другой альтернативы, например, альтернативы X

. С этой целью обратим

внимание на следующее. При любом фиксированном γ



[0; 1] альтернативы X

и X

характеризуются

показателями:

Альтернативы



3 + 5∙γ 9+ 3∙γ 1 + 6∙γ 5

6 + 5∙γ 6 + 3∙γ 1 + 6∙γ 4

Далее, при любом С



[0; 1] оба слагаемые для результирующего показателя модифицированного

критерия, которые соответствуют «крайним» позициям пессимизма и оптимизма, будут определяться

следующим образом:

208

Альтернативы Позиция пессимизма Позиция оптимизма

С∙





5;61min





(9+3∙γ)∙(1-С)

С∙





4;61min





(6+5∙γ)∙(1-С)

Теперь уже легко видеть, что суммарный показатель (как сумма указанных слагаемых для каждого

из альтернативных решений) в рамках рассматриваемого HW

γ(УТ)

-критерия для альтернативы X

всегда

будет больше, чем аналогичный суммарный показатель для альтернативы X

. Действительно, каждое

отдельное слагаемое в результирующем показателе HW

γ(УТ)

-критерия для альтернативы X

, как видим,

является более предпочтительным. Следовательно, и их сумма всегда будет большей для альтернативы X

(по сравнению с альтернативой X

Таким образом, представленный здесь модифицированный HW

γ(УТ)

-критерий не может быть

приемлемым в любых ситуациях. Как видим, еще раз подтверждается уже проиллюстрированное выше

положение. А именно: чем больше будет резерв возможных модификаций указанного типа в арсенале

менеджера, тем более эффективными могут быть процедуры адаптации линий уровня критерия к системе

предпочтений ЛПР. В следующем пункте рассмотрим соответствующие процедуры γ(УТ)-преобразований

линий уровня критерия применительно к критерию произведений.

4. γ(УТ)-модификация для критерия произведений

(Р

γ(УТ)

-критерий)

Соответствующие процедуры γ(УТ)-модификации, которые обусловливают именно частичный

сдвиг семейства линий уровня критерия (к утопической точке поля полезностей), применительно к Р-

критерию произведений реализуются аналогично процедурам такого типа, представленным выше для ММ-

критерия и HW-критерия. Получаемый в результате указанной модификации новый модифицированный

критерий принятия решений в условиях неопределенности далее обозначаем кратко как Р

γ(УТ)

-критерий.

Таким образом, алгоритм оптимизации решения в рамках указанного Р

γ(УТ)

-критерия можно

формализовать такими же шагами. На начальном шаге уточняется конкретное значение коэффициента γ

( ]1;0[





), выбор которого должен быть реализован в соответствии с системой предпочтений ЛПР в

пространстве доходов. Дальнейшие шаги - следующие.

Шаг 1. Применительно к исходной матрице полезностей, которую формализовали для

соответствующей задачи оптимизации решения в условиях неопределенности, по формулам (*), (**) и (***)

реализуются процедуры требуемой γ(УТ)-модификации. В результате получается новая модифицированная

матрица полезностей.

Шаг 2. Для указанной новой модифицированной матрицы полезностей реализуются процедуры

классического Р-критерия. Это означает, что к такой матрице дописывается дополнительный столбец. Его

элементы определяются как произведение элементов соответствующей строки указанной матрицы.

Замечание. Предварительно, если это необходимо, реализуются соответствующие дополнительные

процедуры «модификации новой полученной матрицы полезностей на положительность», т.к. при

использовании Р-критерия имеются соответствующие ограничения.

Шаг 3. По элементам дополнительного столбца модифицированной матрицы полезностей

определяется наилучшее / оптимальное решение. А именно, это – решение, которому соответствует

наилучший (наибольший) показатель в дополнительном столбце указанной матрицы.

Для формального представления семейства линий уровня Р

γ(УТ)

-критерия напомним и уточним

следующую особенность. В контексте соответствующих правил теории принятия решений в условиях

неопределенности процедуры оптимизации, которые соответствуют критерию произведений, требуют иного

представления. Для “линий уровня”, которые характеризуют решение

X , они задаются не как

произведение элементов i-ой строки матрицы полезностей, а как среднее геометрическое таких элементов.

Поскольку затем выбирается решение, для которого такой показатель будет максимальным, то переход к

использованию (на практике) именно показателя произведения (а не среднего геометрического) не изменит

выбора. Тем не менее, представление аппарата линий уровня этого критерия для иллюстрации положений

теории удобно реализовать именно на основе указанного среднего геометрического показателя.

Соответственно, в рамках рассматриваемого здесь Р

γ(УТ)

-критерия семейство линий уровня

критерия будет определяться равенствами типа:

209





Kzvu

zvu



***

;...;;



Здесь

o К – показатель линии уровня;

o γ - выбранный ЛПР показатель коэффициента для частичного сдвига линий уровня

критерия к утопической точке поля полезностей;

o ∆

- соответствующие показатели (применительно к каждой координатной оси),

добавление которых к аргументам критериальной функции, обеспечивает именно100%-ый

сдвиг семейства линий уровня критерия к утопической точке поля полезностей

(





zvu ;...;



Пусть

– вариант возможного решения ЛПР );,...,2,1( mi



– вариант возможной ситуации );,...,2,1( nj



a – доход / прибыль для ЛПР, если будет принято решение i, а ситуация сложится j-ая;



)(

a – соответствующая исходная матрица полезностей для задачи оптимизации.





- требуемые «добавки» к элементам j-го столбца исходной матрицы полезностей при реализации

процедур γ(УТ)-модификации (в рамках предпочтений ЛПР).

Тогда для целевой функции модифицированного критерия имеем:

}{max

)(

УТ

KZ 



где

iji







}{



причем для всех i и j , т.е. для всех элементов новой модифицированной матрицы полезностей

предполагается выполненным неравенство

jij

a 



> 0.

Графическую интерпретацию для семейства линий уровня этого критерия, а также

соответствующие особенности выбора оптимального решения, представьте самостоятельно.

Для иллюстрации численных процедур этого метода рассмотрим (для удобства сравнения

результатов) уже знакомый нам пример.

ПРИМЕР 6.3. Для удобства изложения опять напомним исходные данные в рамках

рассматриваемого примера. А именно, после формализации задачи принятия решений выделено множество

}4,1,{ j



из 4-х случайных событий, которые необходимо учитывать в рамках соответствующих

решений. Кроме того, пусть анализируются 6 альтернативных решений }6,1,{ iX

, из которых требуется

выбрать наилучшее. При этом соответствующая матрица полезностей имеет вид:

Доходы при событиях:

Решения



5 4 3 3

6 2 6 4

-3 6 2 12

3 9 1 5

7 1 5 3

6 6 1 4

210

Найдем наилучшее решение по Р

γ(УТ)

-критерию применительно к ситуации, когда, например, ЛПР

для параметра γ (в рамках указанной модификации классического критерия пессимизма) выбирает значение

γ= 0,8.

Шаг 1. Сначала подчеркнем, что соответствующая утопическая точка в поле полезностей

применительно к этой задаче остается прежней (см. примеры 6.1 - 6.2), т.е. имеет координаты:

= (7; 9; 6; 12).

Соответственно и показатели

 для величин «сдвигов» по j-ой координатной оси в пространстве

доходов (для случая 100%-ой реализации таких сдвигов), определяемые формулами (*), остаются

прежними:

 = 12 – 7 = 5;

 = 12 – 9 = 3;

 = 12 – 6 = 6;

 = 12 – 12 = 0.

После этого определяем показатели )(



 =





с учетом требований ЛПР применительно к

частичной реализации соответствующего сдвига (здесь в этом примере - 80% вместо 100% при указанных

значениях

 ):

)(



 = 0,8∙5 = 4; )(



 = 0,8∙3 = 2,4;

)(



 = 0,8∙6 = 4,8; )(



 = 0,8∙0 = 0.

Наконец, с учетом формул (****) для перехода к новым элементам матрицы, выписываем

соответствующую модифицированную матрицу полезностей:

Доходы при событиях:

Решения



9 6,4 7,8 3

10 4,4 10,8 4

1 8,4 6,8 12

7 11,4 5,8 5

11 3,4 9,8 3

10 8,4 5,8 4

Шаг 2. Для указанной новой модифицированной матрицы полезностей реализуем процедуры

интересующего нас Р-критерия. Подчеркнем, что все элементы новой модифицированной матрицы

полезностей являются положительными. Соответственно предварительные процедуры «модификации на

положительность» не требуются. Произведения элементов матрицы по строкам представлены в

соответствующем дополнительном ее столбце.

Доходы при событиях:

Решения



Показатель

γ(УТ)

критерия