Бродецкий Г.Л. Системный анализ в логистике. Выбор в условиях неопределенности
Подождите немного. Документ загружается.


191
Дополнительно в этом пункте отметим ещё одну особенность, связанную с возможностями
использования представленного ММ
γ(УТ)
-критерия. А именно, зная выбор конкретного ЛПР, который был
сделан им применительно к определённой задаче принятия решений в условиях неопределённости, можно
получать оценки для допустимых значений параметра γ применительно к системе предпочтений этого ЛПР.
Другими словами, можно определять, на сколько процентов следует реализовать «сдвиг» семейства линий
уровня критерия к утопической точке поля полезностей с учетом системы предпочтений ЛПР. Такой подход
позволяет оценивать и уточнять применительно к конкретному ЛПР (по результатам известных бывших и
последующих выборов) соответствующий характер его линий уровня. В частности, по значениям
указанного параметра можно интерпретировать степень склонности ЛПР к более оптимистическим
решениям (ближайшим к утопической точке поля полезностей) и степень склонности ЛПР к осторожным
классическим решениям. Для иллюстрации соответствующего подхода к оценке параметра «γ» снова
вернемся к условиям нашего примера.
ПРИМЕР 6.1 (Дополнение: иллюстрация процедур оценки коэффициента γ в формате
предпочтений ЛПР для критерия пессимизма). Рассмотрим упрощенную ситуацию, которая обсуждалась
выше в качестве условного примера, когда после формализации задачи принятия решений в условиях
неопределенности было выделено множество }4,1,{ j
j
из 4-х случайных событий. При этом,
напомним, выбиралось лучшее решение из 6 альтернативных решений }6,1,{ iX
i
.
Пусть, например, в рамках этой ситуации известно, что некоторое ЛПР выбирает только именно
альтернативу X
4
. Оценим возможный диапазон значений для параметра γ применительно к этому ЛПР. Для
этого предварительно дополним исходную матрицу полезностей примера одним дополнительным
столбцом, в котором представим показатели ММ
γ(УТ)
-критерия как функции переменной γ в области
]1;0[
. Соответствующие процедуры представлены ниже:
Доходы при событиях:
Решения
1
2
3
4
Показатель
ММ
γ(УТ)
-критерия как
функция
от γ
X
1
5 4 3 3
3 (при любом ]1;0[
)
X
2
6 2 6 4
min {2+3∙γ; 4}
X
3
-3 6 2 12
-3 + 5∙γ
X
4
3 9 1 5
min {1+6∙γ; 5}
X
5
7 1 5 3
min {1+3∙γ; 3}
X
6
6 6 1 4
min {1+6∙γ; 4}
Теперь воспользуемся тем, что согласно условию, ЛПР выбрало альтернативу X
4
. В контексте
данного модифицированного ММ
γ(УТ)
-критерия это означает, что показатель min {1+6∙γ; 5} (см. строку,
соответствующую альтернативе X
4
) оказался самым большим из всех показателей дополнительного
столбца. Следовательно, можно выписать следующую систему линейных неравенств относительно
неизвестного значения γ:
min {1+6∙γ; 5} > 3;
min {1+6∙γ; 5} > min {2+3∙γ; 4};
min {1+6∙γ; 5} > -3 + 5∙γ;
min {1+6∙γ; 5} > min {1+3∙γ; 3};
min {1+6∙γ; 5} > min {1+6∙γ; 4}.
192
Решение этой системы неравенств представлено на рис. 6.3 (графическим методом). Для удобства
приняты следующие сокращения:
f
1
= f
1
(γ) = 3;
f
2
= f
2
(γ) = min {2+3∙γ; 4};
f
3
= f
3
(γ) = -3 + 5∙γ;
f
4
= f
4
(γ) = min {1+6∙γ; 5};
f
5
= f
5
(γ) = min {1+3∙γ; 3};
f
6
= f
6
(γ) = min {1+6∙γ; 4}.
При этом легко видеть, что в этих специальных обозначениях интересующая нас система
неравенств имеет следующий вид:
f
4
> f
1
f
4
> f
2
f
4
> f
3
f
4
> f
5
f
4
> f
6
Рисунок 6.3 наглядно иллюстрирует, что решением указанной системы неравенств является
следующая область значений параметра γ:
]1;5,0(
.
Итак, приемлемым для такого ЛПР будет некоторое значение
из области ]1;5,0(
, т.к. в
рассматриваемой ситуации оптимальный выбор по модифицированному ММ
γ(УТ)
-критерию будет давать
именно только альтернативу X
4
. Продолжая аналогичные процедуры, но уже применительно к другим
ситуациям бизнеса, можно далее уточнять для этого ЛПР соответствующую оценку неизвестного
коэффициента
.
Представленная модификация ММ
γ(УТ)
-критерия не претендует на исключительную
универсальность. Другими словами, мы должны специально подчеркнуть, что на практике не исключены
следующие ситуации. Альтернативное решение, которое предпочитает ЛПР (соответственно оно,
естественно, будет недоминируемым), может оказаться таким, что оно не будет выбрано
модифицированным ММ
γ(УТ)
-критерием ни при каком значении коэффициента ]1;0[
. Для адаптации к
предпочтениям такого ЛПР менеджеру возможно понадобятся аналогичные модификации, но уже
применительно к другим критериям принятия решений в условиях неопределенности. Проиллюстрируем
это положение применительно к рассматриваемой в этом примере ситуации.
Предварительно напомним, что во введении уже подчеркивалось, что различные ЛПР имеют,
вообще говоря, различное отношение к риску (а соответственно и к возможным отклонениям конечного
экономического результата). Поэтому в одной и той же ситуации их предпочтения могут существенно
отличаться.
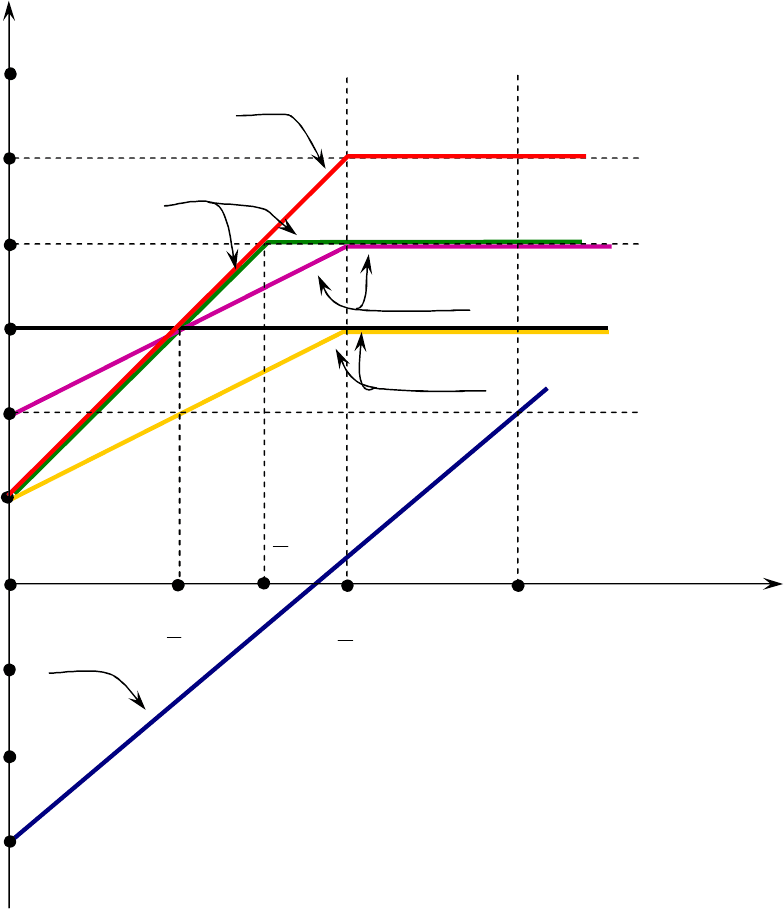
193
Итак, рассмотрим здесь теперь ситуацию, когда в условиях этого примера ЛПР предпочитает,
например, только именно альтернативу X
5
, а не какую-нибудь другую альтернативу из анализируемого
множества альтернативных решений. Подчеркнем, что никакое другое решение не доминирует при этом
альтернативу X
5
. Тогда соответственно необходимо рассматривать систему неравенств, которая
применительно к введенным ранее обозначениям будет иметь вид:
f
5
> f
1
f
5
> f
2
f
5
> f
3
f
5
> f
4
f
5
> f
6
γ
6
5
4
3
2
1
-
3
-
2
-
1
0
f
f
3
f
4
f
1
f
6
f
2
f
5
3
1
2
1
3
2
1
Рис. 6.3. Графическое решение системы неравенств
(в области
]1;0[
)
194
Из рис. 6.3 легко видеть, что указанная система неравенств не имеет решения в области ]1;0[
.
Действительно, при любом значении коэффициента γ (в указанной области ]1;0[
) выполнено строгое
неравенство f
2
> f
5
. Поскольку при оптимизации альтернативного решения выбирается наибольший такой
показатель, то этого неравенства достаточно, чтобы понять, что в рамках нашего примера альтернатива X
5
,
не будет выбрана в качестве оптимальной, ни при каком значении параметра ]1;0[
.
Наконец, дополнительно подчеркнем также следующее.
Пусть в условиях этого дополнения к примеру 6.1 анализируется ситуация, когда ЛПР наверняка
предпочитает только именно альтернативу X
2
(а не X
4
и не X
5
). Тогда потребуется решать следующую
систему неравенств
f
2
> f
1
f
2
> f
3
f
2
> f
4
f
2
> f
5
f
2
> f
6
Из рис. 6.3 видно, что указанная система неравенств не имеет решения. Соответственно выбрать
приемлемое значение параметра
для такого ЛПР не представляется возможным.
Модифицируем это условие в рамках нашего примера следующим образом. Пусть в условиях этого
дополнения к примеру 6.1 анализируется ситуация, когда ЛПР предпочитает альтернативу X
2
, но строгой
уверенности в этом у него нет. Тогда соответствующая система неравенств будет нестрогой. Легко видеть,
что в этом случае получаем единственное решение: γ = 1/3.
Означает ли это, что модифицированный ММ
γ(УТ)
-критерий при γ = 1/3 , как раз, и соответствует
системе предпочтений указанного ЛПР? Вряд ли. Столь жесткие такие требования к приемлемому
значению коэффициента γ в рамках указанной модификации при первой же «выборке», скорее всего,
подчеркивают следующее. В этом случае, как и в случае выбора альтернативы X
5
, для более адекватной
адаптации к системе предпочтений ЛПР следует, возможно, рассматривать аналогичные модификации, но
уже применительно к другим критериям принятия решений в условиях неопределенности.
Рассмотренную здесь модификацию ММ
γ(УТ)
-критерия имеет смысл анализировать для таких ЛПР,
которые в условиях примера 6.1, если и сомневаются в выборе оптимального решения, то только
применительно к альтернативам X
1
, X
4
и X
6
(остальные для них без сомнения явно неприемлемы). Как
видим, выбор для ЛПР приемлемого критерия или соответствующей его модификации может потребовать
от менеджера тщательного и кропотливого анализа. При этом менеджеру необходимо владеть всем
арсеналом доступных для выбора критериев принятия решений в условиях неопределенности, а также всеми
наборами соответствующих приемов и методов модификации таких критериев.
Соответствующие γ(УТ)-модификации будут далее представлены применительно к остальным
указанным в начале главы критериям.
Дополнительная специфика процедур выбора наилучшего решения
на основе ММ
γ(УТ)
-критерия
Как и в случае рассмотренного в первой главе классического ММ-критерия, отметим здесь
дополнительно важную особенность, характерную для процедур оптимального выбора по
модифицированному ММ
γ(УТ)
-критерию. Соответствующая особенность еще раз подчеркнет, что термин
«крайний» для классического ММ-критерия и в этом случае специальной модификации также может иметь
дополнительную специфическую смысловую нагрузку, вполне аналогичную той, которая была отмечена в
первой главе.
А именно, и в этом случае линии уровня представленного здесь модифицированного критерия
занимают «крайнее» положение по отношению к соответствующим конусам предпочтений. Тот факт, что
вершины таких угловых линий уровня смещены относительно биссектрисы главного координатного угла (в
отличие от ММ-критерия, чтобы «сместить» выбор ближе к утопической точке поля полезностей), не
195
устраняет отмеченную ранее особенность выбора наилучших решений, обусловливаемую соответствующим
«крайним» положением для линий уровня критерия. Поэтому, указанная особенность снова относится к
ситуации, когда окажется, что максимальное значение целевой функции (теперь - функции Z
ММ γ(УТ)
)
соответствующего модифицированного ММ
γ(УТ)
-критерия достигается не на одном единственном решении
из множества Х
1
- Х
m
, а одновременно на нескольких альтернативных решениях, представленных в матрице
полезностей.
Действительно, если при реализации алгоритма ММ
γ(УТ)
-критерия будет найдено несколько
альтернатив с одинаковым наилучшим значением показателя указанной целевой функции, то снова, как и
для ММ-критерия, можно столкнуться с противоречивой ситуацией. А именно: пусть, например, оказалось,
что решения
*
X и
**
X имеют одинаковый (причем, - наилучший для всего множества анализируемых
альтернативных решений) показатель соответствующей целевой функции Z
ММ γ(УТ)
. Тогда снова возможны
следующие случаи.
1. Одно из этих решение может оказаться доминируемым. Разумеется, ЛПР не станет его
использовать. Поэтому в такой ситуации в качестве оптимального решения всегда будет принято
доминирующее его решение.
2. Среди этих решений
*
X и
**
X может не быть доминируемых. Соответственно, любая из этих
альтернатив может быть принята в качестве оптимального решения по ММ
γ(УТ)
-критерию.
Графические иллюстрации таких ситуаций приведите самостоятельно (они вполне аналогичны тем,
которые были проиллюстрированы ранее в главе 1).
Соответственно и алгоритм выбора оптимального решения на основе ММ
γ(УТ)
-критерия должен быть
дополнен процедурой идентификации решения на оптимальность. Ее формализация здесь опускается. Такая
процедура также полностью соответствует приведенной выше такой процедуре применительно к ММ-
критерию.
ПРИМЕР 6.1 (Специальное дополнение: иллюстрация процедур идентификации оптимального
решения для ММ
γ(УТ)
-критерия). Пусть в условиях примера 6.1 множество анализируемых альтернативных
решений содержит не шесть, а девять альтернативных решений Х
1
- Х
9
, которые представлены
соответствующей матрицей полезностей:
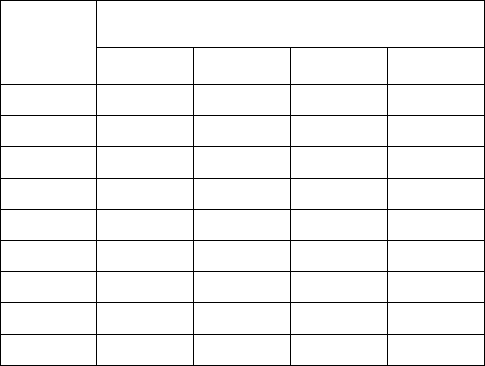
Доходы при событиях:
Решения
1
2
3
4
X
1
5 4 3 3
X
2
6 2 6 4
X
3
-3 6 2 12
X
4
3 9 1 5
X
5
7 1 5 3
X
6
6 6 1 4
X
7
2 5 -3 12
X
8
2 9 3 5
X
9
2 8 3 5
Реализуем процедуры модифицированного ММ
γ(УТ)
-критерия при γ = 0,5 для нахождения
соответствующего оптимального альтернативного решения.
Шаг 1. Для утопической точки соответствующего поля полезностей координаты остаются
прежними (как и непосредственно в примере 6.1):
Х
У
= (7; 9; 6; 12).
Соответственно при γ = 0,5 получаем такие же показатели для «частичных сдвигов» )(
*
j
по
координатным осям в пространстве доходов, как и те, которые были найдены ранее, - непосредственно в
примере 6.1:
)(
*
1
= 0,5∙5 = 2,5; )(
*
2
= 0,5∙3 = 1,5;
196
)(
*
3
= 0,5∙6 = 3; )(
*
4
= 0,5∙0 = 0.
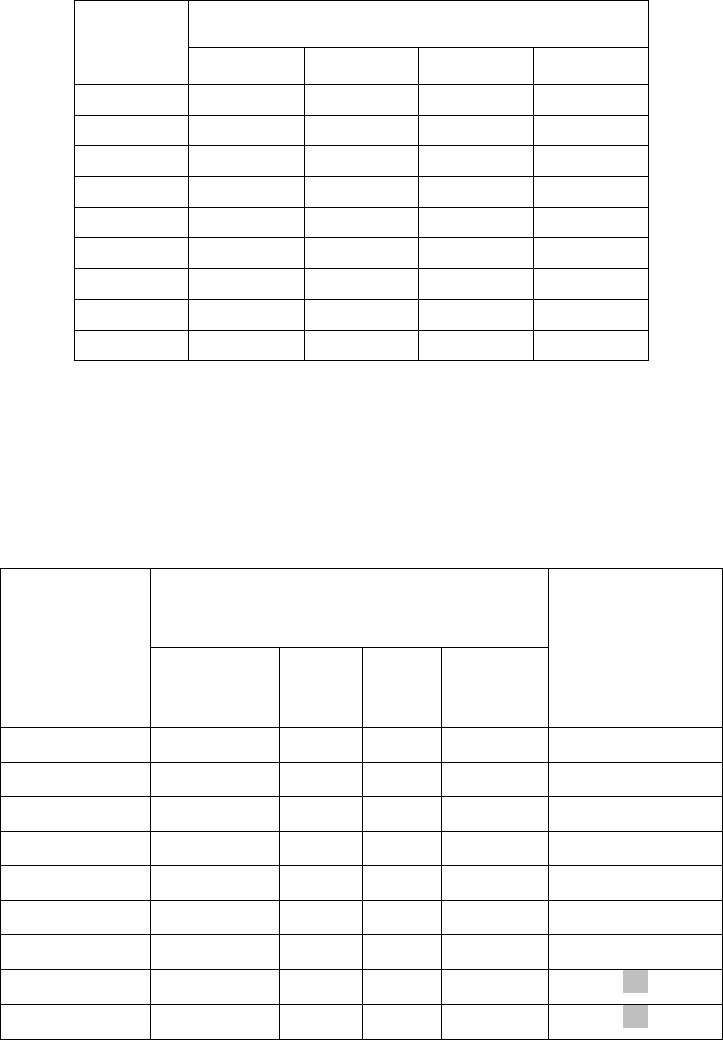
Поэтому для модифицированной матрицы полезностей в этом случае имеем:
Доходы при событиях:
Решения
1
2
3
4
X
1
7,5 5,5 6 3
X
2
8,5 3,5 9 4
X
3
-0,5 7,5 5 12
X
4
5,5 10,5 4 5
X
5
9,5 2,5 8 3
X
6
8,5 7,5 4 4
X
7
4,5 6,5 0 12
X
8
4,5 10,5 6 5
X
9
4,5 9,5 6 5
Шаг 2. Для указанной новой модифицированной матрицы полезностей в соответствии с алгоритмом
оптимизации реализуем требуемые процедуры классического ММ-критерия. Они представлены элементами
соответствующего дополнительного столбца: его дописываем к такой модифицированной матрице
полезностей.
Доходы при событиях:
Решения
1
2
3
4
Показатель
ММ
γ(УТ)
-критерия
X
1
7,5 5,5 6 3
3
X
2
8,5 3,5 9 4
4
X
3
-0,5 7,5 5 12
-0,5
X
4
5,5 10,5 4 5
4
X
5
9,5 2,5 8 3
3
X
6
8,5 7,5 4 4
4
X
7
4,5 6,5 0 12
0
X
8
4,5 10,5 6 5
4,5
X
9
4,5 9,5 6 5
4,5
Итак, в этой ситуации, как видим, наилучшее значение показателя ММ
γ(УТ)
-критерия достигается
одновременно у двух альтернатив: X
8
и X
9
(показатель равен 4,5 и выделен в дополнительном столбце
матрицы). Реализация требуемых в таком случае процедур идентификации этих решений на оптимальность
приводит к следующему. Альтернатива X
8
доминирует альтернативу X
9
. Поэтому последняя из указанных
альтернатив не может быть принята в качестве оптимальной. Соответственно, в этой ситуации оптимальным
решением по модифицированному ММ
γ(УТ)
-критерию является альтернативное решение X
8
.
197
3. γ(УТ)-модификация для критерия Гурвица
(HW
γ(УТ)
-критерий)
Представим особенности реализации соответствующих процедур γ(УТ)-модификации, которые
обусловлены именно частичным сдвигом семейства линий уровня критерия (к утопической точке поля
полезностей), применительно к HW-критерию Гурвица. Получаемый в результате такой модификации
новый модифицированный критерий принятия решений в условиях неопределенности обозначаем кратко
как HW
γ(УТ)
-критерий.
Подчеркнем, что в такой ситуации алгоритм оптимизации альтернативного решения в рамках
указанного HW
γ(УТ)
-критерия можно характеризовать следующими шагами.
На начальном шаге (как и в предыдущем случае) уточняется конкретное значение коэффициента γ
( ]1;0[
), выбор которого (см. далее иллюстрацию в примере 6.2 - Дополнение) должен быть реализован
ЛПР в соответствии со своей системой предпочтений в пространстве доходов. Кроме того, в соответствии с
рекомендациями главы 2 формализуется значение приемлемого для ЛПР «весового» коэффициента С в
рамках технологии критерия Гурвица. Дальнейшие процедуры можно представить следующими шагами.
Шаг 1. Применительно к исходной матрице полезностей, которую формализовали для
соответствующей задачи оптимизации решения в условиях неопределенности, по формулам (*), (**) и (***)
реализуются процедуры требуемой γ(УТ)-модификации. В результате получается новая модифицированная
матрица полезностей.
Шаг 2. Для указанной новой модифицированной матрицы полезностей реализуются процедуры
описанного в главе 2 HW-критерия Гурвица. Это означает, что к такой матрице дописываются три
дополнительных столбца. А именно:
4. первый – для оценок по классическому ММ-критерию (напомним, что его элементы определяются
как самые плохие, т.е. наименьшие, из возможных конечных экономических результатов при
соответствующем решении);
5. второй – для оценок по классическому Н-критерию (напомним, что его элементы определяются
как самые хорошие, т.е. возможные наибольшие конечные экономические результаты при
соответствующем решении);
6. третий – для результирующих “взвешенных” оценок модифицированной матрицы по HW-
критерию с учетом выбранных «весов» применительно к первым двум из указанных выше типов
оценок.
Шаг 3. По элементам синтезированного третьего дополнительного столбца модифицированной
матрицы полезностей определяется наилучшее / оптимальное альтернативное решение. А именно, это –
решение, которому соответствует наилучший (наибольший) показатель в дополнительном столбце
указанной матрицы.
Соответственно, в рамках рассматриваемого здесь HW
γ(УТ)
-критерия семейство линий уровня
критерия будет определяться равенствами типа:
***
;...;;min
zvu
zvuс
Кzvuс
zvu
***
;...;;min)1(
Здесь
o К – показатель линии уровня;
o γ - выбранный ЛПР показатель коэффициента для «частичного» сдвига линий уровня
критерия к утопической точке поля полезностей;
o ∆
α
- соответствующие показатели (применительно к каждой координатной оси),
добавление которых к аргументам критериальной функции, обеспечивает именно100%-ый
сдвиг семейства линий уровня критерия к утопической точке поля полезностей
(
zvu ;...;
).
Пусть
i
– вариант возможного решения ЛПР );,...,2,1( mi
j
– вариант возможной ситуации );,...,2,1( nj
ij
a – доход / прибыль для ЛПР, если будет принято решение i, а ситуация сложится j-ая;

198
A
)(
ij
a – соответствующая исходная матрица полезностей для задачи оптимизации.
*
j
- требуемые «добавки» к элементам j-го столбца исходно матрицы полезностей при реализации
процедур γ(УТ)-модификации (в рамках предпочтений ЛПР).
Тогда для целевой функции модифицированного HW
γ(УТ)
-критерия имеем:
}{max
)(
i
i
УТ
HW
KZ
,
где
**
max)1(}{min
jij
j
j
aсaсK
ij
j
i
;
с - соответствующий “весовой” коэффициент, который выбирается ЛПР;
γ - соответствующий коэффициент для γ(УТ)-преобразования,
который адаптирован к предпочтениям ЛПР.
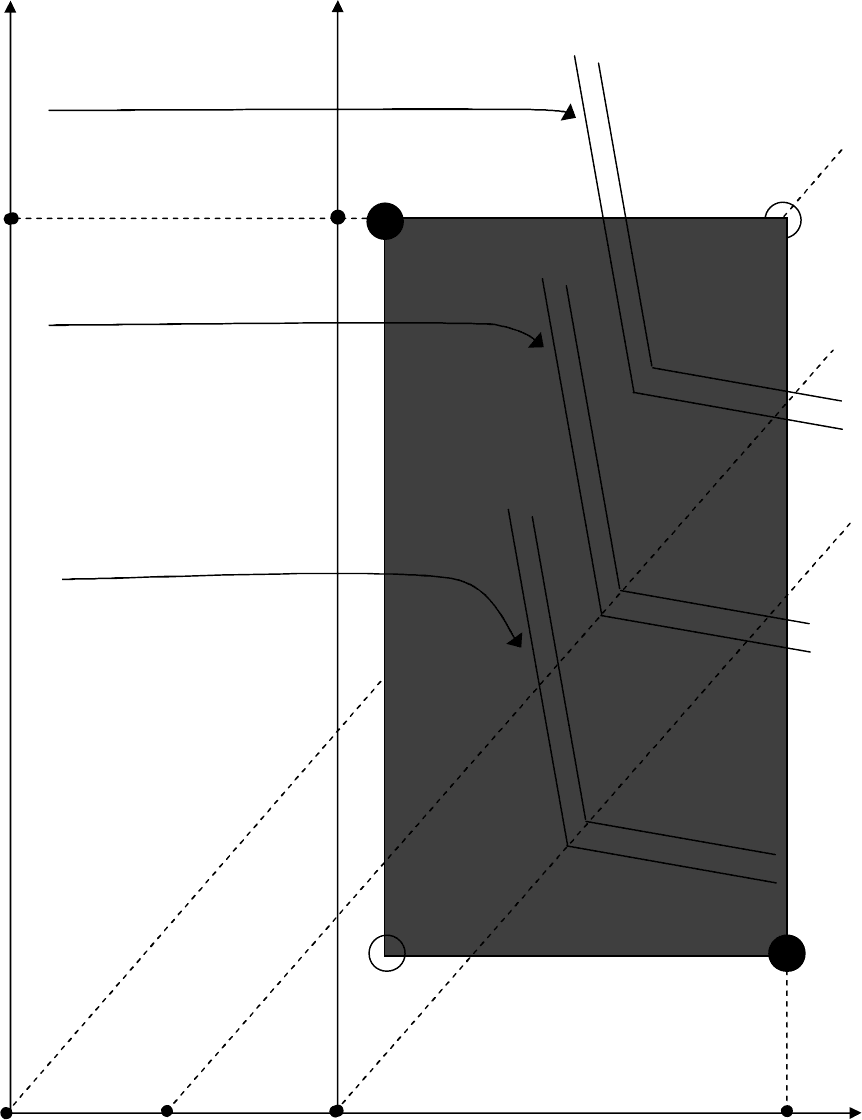
Графическая интерпретация для семейства линий уровня этого критерия, а также соответствующие
особенности выбора оптимального решения, представлены на рис. 6.4 и 6.5.
Иллюстрацию численных процедур этого метода рассмотрим (для удобства сравнения результатов)
на том же примере, который уже был использован выше.
ПРИМЕР 6.2. Для удобства изложения напомним исходные данные в рамках рассматриваемого
примера. А именно, после формализации задачи принятия решений выделено множество }4,1,{ j
j
из 4-
х случайных событий, которые необходимо учитывать в рамках соответствующих решений. Кроме того,
пусть анализируются 6 альтернативных решений }6,1,{ iX
i
, из которых требуется выбрать наилучшее.
При этом соответствующая матрица полезностей имеет вид:
Доходы при событиях:
Решения
1
2
3
4
X
1
5 4 3 3
X
2
6 2 6 4
X
3
-3 6 2 12
X
4
3 9 1 5
X
5
7 1 5 3
X
6
6 6 1 4
199
Линии уровня
HW
-
критерия
при γ=1 (100%-й сдвиг)
Линии уровня
HW
-
критерия
при γ=0.5 (50%-й сдвиг)
Линии уровня
HW
-
критер
ия
при γ=0 (без сдвига)
U
max
нов
vax
U
U
V
нов
V
1
нов
V
max
max
V
нов
1
0
нов
5.0
0
0
45
0
УТ
Рис. 6.4. Иллюстрация частичного сдвига линий уровня HW-критерия
200
Найдем наилучшее решение по модифицированному HW
γ(УТ)
-критерию применительно к ситуации,
когда, например, для «весового» коэффициента «с» в рамках технологии критерия Гурвица ЛПР выбирает
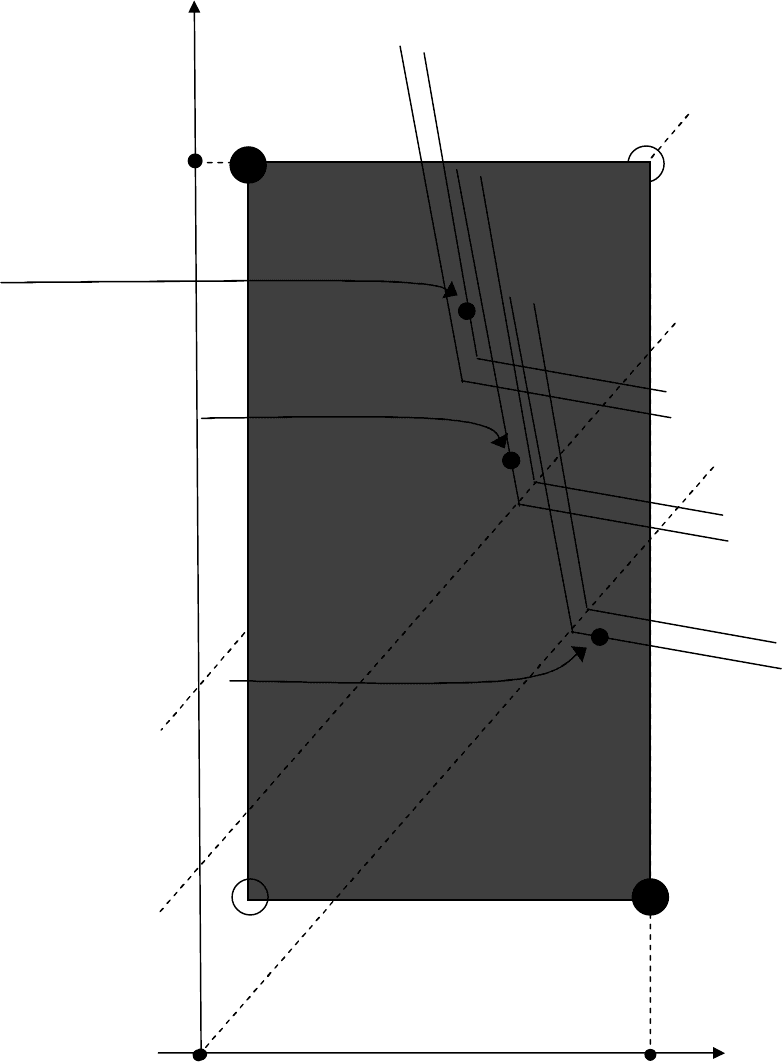
Рис. 6.5. Иллюстрация оптимального выбора по модифицированному
HW-критерию при сдвиге его линий уровня
Выбор по
HW
(γ=1)
-критерию
U
max
U
V
max
V
0
45
0
УТ
Выбор по
HW
(γ=0,5)
-критерию
Выбор по
HW
(γ=0)
-критерию
