Brewster H.D. Mathematical Physics
Подождите немного. Документ загружается.


122
Linear
Algebra
A=
(~1
:J.
We note that x is a diagonal matrix.
Now,
we
seek a transformation between x and y that will transform the
coupled system into the uncoupled system. Thus, we define the transformation
x=Sy.
Inserting this transformation into the coupled system we have
d
-x
=Ax
=>
dt
d
-Sy
=ASy=>
dt
d
S
dtY
=ASy.
Multiply both sides by
S-l.
[We can do this
if
we
are dealing with
an
invertible transformation, i.e., a transformation in which we can get y from x
as y = S-lx.] We obtain
Noting that
d
dt y
= S-lASy.
d
-y=Ay
dt '
we have A = S-lAS.
The expression
S-lAS
is called a similarity transformation
of
matrix A.
So, in order to uncouple the system, we seek a similarity transformation
that
results in a diagonal matrix. This process is called the diagonalization
of
matrix
A.
We do not know S, nor do
we
know A. We can rewrite this equation as
AS=SA.
We can solve this equation
if
S is real symmetric, i.e,
ST
=
S.
[In the case
of
complex matrices, we need the matrix to be Hermitian,
ST
= S where the
bar denotes complex conjugation. We first show that
SA =
AS.
We look
at
the
ijth component
of
SA
and rearrange the terms in the matrix product.
n
=
LSikAjlkj
k=l
n
=
LAjljkSL
k=l

Linear
Algebra
n
=
IAjkS
ki
= (AS)ij
k=1
This result leads us to the fact that S satisfies the equation
AS=AS:
Therefore, one has that the columns
of
S (denoted v) satisfy an
equation
of
the form
Av
=
Av.
123
This is an equation for vectors v and numbers A given matrix A. It is
called an eigenvalue problem. The vectors are called eigenvectors and the
numbers,
A,
are called eigenvalues. In principle, we can solve the eigenvalue
problem and this will lead
us
to solutions
of
the uncoupled system
of
differential
equations.
Example
of
an
Eigenvalue
Problem
We will determine the eigenvalues and eigenvectors for
(
1
-2)'
A =.
-3
2
In order to find the eigenvalues and eigenvectors
of
this equation, we
need to solve
Av
=
Av.
Let v
=(:J
. Then the eigenvalue problem can be written out. We have
that
Av
=
Av.
(
VI
-
2V
2)
(Avl)
-3vI +
2v2
=
Av2
.
So, we see that our system becomes
VI
-
2v2
=
Av
l
,
-3v
I
+
2v2
=
Av
2
·
This can be rewritten as
(1
-
A)v
I
-
2v2
=
0,
-3v
I
+
(2
-
A)v
2
=
O.
This is a homogeneous system. We can try to solve it using elimination,
as we had done earlier when deriving Cramer's Rule. We find that multiplying
the first equation by 2 -
A,
the second by 2 and adding, we get
[(1
-
1.,)(2
-
A)
-
6]vI
=
0:
If
the factor
in
the brackets is not zero, we obtain
VI
=
O.
Inserting this

124
Linear
Algebra
into the system gives v
2
= 0 as well. Thus, we find v is the zero vector. However,
this does not get us anywhere.
We
could have guessed this solution. This simple
solution is the solution
of
all eigenvalue problems and is called
the
trivial
solution. When solving eigenvalue problems,
we
only look for nontrivial
solutions!
So, we have to stipulate that the factor in the brackets is zero.
This
means
that
VI
is still unknown.
This
situation will always
occur
for eigenvalue
problems. The general eigenvalue problem can be written as
AV-AV
= 0,
or
by
inserting the identity matrix,
Av
-
/Jv
=
O.
Finally, we see that
we
always get a homogeneous system,
(A
- Al)v =
O.
The
factor that has to
be
zero
can
be seen now as the determinant
of
this
system. Thus,
we
require
det(A -
AI)
=
O.
We write out this condition for the example
at
hand. We have
that
I
I-A
-21
=
-3
2-A
O.
This will always be the starting point in solving eigenvalue problems.
Note
that the matrix is A with
A'S
subtracted from the diagonal elements.
or
Computing the determinant,
we
have
(l
- A)(2 -
A)
- 6 = 0,
A2
-
3A-
4 =
O.
We therefore have obtained a condition on the eigenvalues! It is a quadratic
and
we
can factor it:
(A
- 4
)(A
+
1)
=
O.
So, our eigenvalues are A = 4,
-I.
The
second step is to find the eigenvectors.
We
have to do this for each
eigenvalue.
We
first insert A = 4 into
our
system:
-3v
I
-
2v2
=
0,
-3v\
-
2v2
=
O.
Note that these equations are the same. So,
we
have one equation in two
unknowns.
We
will not get a unique solution. This is typical
of
eigenvalue
problems. We can pick anything we want for v
2
and then determine
VI'
For
example, v
2
-
I gives
VI
=
-2/3.
A nicer solution would be v
2
= 3 and
VI
=
-2:
These vectors are different, but they point in the same direction in the
VI
v
2
plane.
For
A =
-1,
the
system becomes

Linear
Algebra
2vI -
2v2
= 0,
-3v
I
+ 3v
2
=
o.
125
While these equations do not at first look the same,
we can
divide
out
the
constants and see that
once
again
we
get the same equation,
vI
= v
2
·
Pickingv
2
=
1,
we
get
vI
=
1.
In summary, the solution to
our
eigenvalue problem is
A=4'V=(~1)
A=-l,V=G)
Eigenvalue Problems
In the last subsection
we
were
introduced to eigenvalue problems as a
way
to obtain a solution to a
coupled
system
of
linear differential equations.
Eigenvalue problems appear in
many
contexts in physical applications. In the
next subsection
we
will look at
another
problem
that
is a bit more geometric
and will give us more insight into the process
of
diagonalization.
We
seek
nontrivial solutions to
the
eigenvalue problem
Av=
AV.
We
note
that
v = 0 is an obvious solution. Furthermore, it does not lead
to anything useful. So, it is a trivial solution. Typically,
we
are given the matrix
A and have to determine the eigenvalues,
A,
and the associated eigenvectors,
v,
satisfying the above eigenvalue problem.
For
now we begin
to
solve the eigenvalue problem for v =
(:~)
. Inserting
this into equation,
we
obtain the homogeneous algebraic system
(a -
A)V
I
+ bv
2
=
0,
eV
I
+
(d
-
A)v2=
o.
The
solution
of
such a system would be unique
if
the determinant
of
the
system is not zero. However, this
would
give the trivial solution
VI
= 0, v
2
=
o.
To
get a nontrivial solution,
we
need to force the determinant to be zero. This
yields the eigenvalue equation
o
l
a-A
b I
= = (a - A)(d -
A)
- be.
e
d-A
This
is a
quadratic
equation
for the
eigenvalues
that
would
lead
to
nontrivial solutions.
If
we
expand the right side
of
the equation, we find that
A2
- (a + d)A +
ad
- be =
O.
This is the same equation as the characteristic equation for the general

126
Linear
Algebra
constant coefficient differential equation. Thus, the eigenvalues correspond
to the solutions
of
the characteristic polynomial for the system.
Once
we
find the eigenvalues, then there are possibly an infinite number
solutions to the algebraic system.
We
will see this in the examples.
The method for solving eigenvalue problems, as you have seen, consists
of
just
a few simple steps. We list these steps as follows:
• Write the coefficient matrix,
• Find the eigenvalues from the equation det(A -
II)
= 0, and,
• Solve the linear system
(A
-lJ)v
= 0 for each
A:
Rotations of Conics
You
may have seen the general form for
the
equation
of
a conic in
Cartesian coordinates in your calculus class.
It
is given by
Ax2 +
2Bxy
+
Cy
+
Ex
+
Fy
= D.
This equation
can
describe a variety
of
conics (ellipses, hyperbolae
and
parabolae) depending
on
the constants.
The
E
and
F terms result from a
translation
of
the origin and the B
term
is
the
result
of
a rotation
of
the
coordinate system. We leave it to the reader to show that coordinate translations
can
be made to eliminate the linear terms. So,
we
will set E = F = 0 in
our
discussion and
only
consider quadratic equations
of
the
form
Ax2 +
2Bxy
+ Cy2 = D.
If
B = 0, then the resulting equation could be an equation for the standard
ellipse or hyperbola with centre
at
the origin. In the case
of
an ellipse, the
semimajor and semiminor axes lie along the coordinate axes. However, you
could rotate the ellipse and
that
would introduce a B term, as we will see.
This conic equation can be written in matrix form. We note that
(x
y)(B
A
CB)(Xy)
= Ax2 +
2Bxy
+
Cy:
In short hand matrix form,
we
thus have for
our
equation
x
T
Qx
=D,
where Q is the matrix
of
coefficients A, B, and
C.
We
want
to determine the transformation
that
puts this conic into a
coordinate system in which there is no
B term. Our goal is to obtain
an
equation
of
the form
A'x'2 + C' y'2=
D'
in the new coordinates yT = (x',
y').
The matrix form
of
this equation is given
as
T(A'
0)
,
y 0
C'
y=D.
We
will denote the diagonal matrix
by
A.

Linear
Algebra
So, we let
x=Ry,
127
where R is a rotation matrix. Inserting this transformation into our equation
we find that
x
T
Qx
= (Ry)TQRy
=
yT
(RT
QR)y.
Comparing this result to to desired form, we have
A=RTQR.
Recalling
that
the
rotation
matrix
is
an
orthogonal
matrix,
RT
=
kl,
we
have
A=kIQR.
Thus, the problem reduces to that
of
trying to diagonalize the matrix
Q.
The eigenvalues
of
Q will lead to the constants in the rotated equation and the
eigenvectors, as we will see, will give the directions
of
the principal axes (the
semimajor and semiminor axes). We will first show this
in
an example.
Example: Determine the principle axes
of
the ellipse given by
13x
2
-
10xy +
By
-72
=
o.
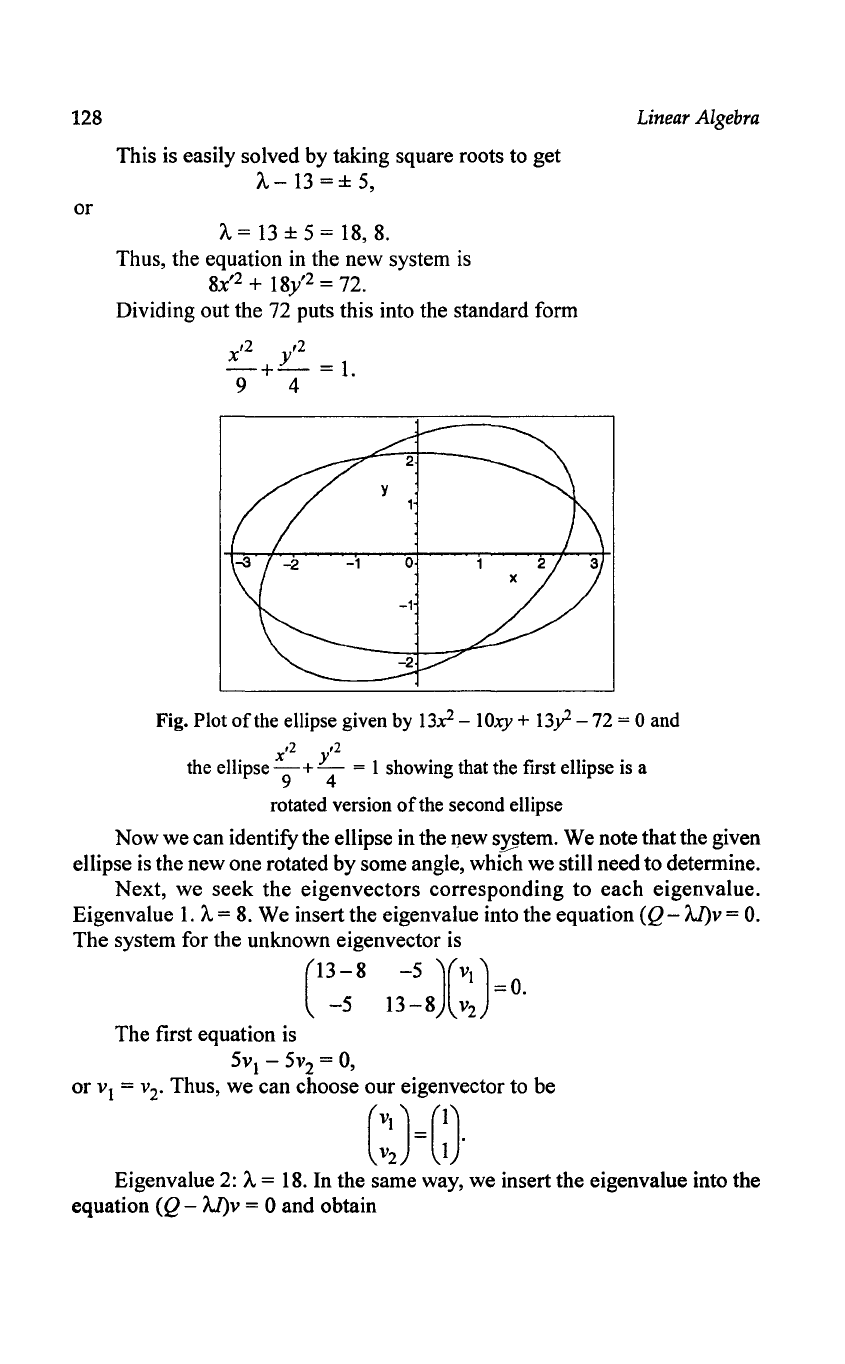
A plot
of
this conic
in
figure shows that it is an ellipse. However, we
might not know this without plotting it.
If
the equation were in standard form,
we could identify its general shape. So, we will use the method outlined above
to find a coordinate system
in
which the ellipse appears in standard form.
The coefficient matrix for this equation
is
given by
Q=(~~
~:).
We seek a solution to the eigenvalue problem:
Qv
=
Av.
Recall, the first
step is to get the eigenvalue equation from det(Q
-IJ)
=
0:
For this
Fig. Plot
of
the Ellipse Given by
13x2
- IOxy +
13y
-
72
= 0
problem we have
1
13-"-
-51
=
-5
13-"-
O.
So, we have to solve
(13 -
A)2
- 25 =
O.
128
or
This is easily solved by taking square roots to get
A-13
=±
5,
A =
13
± 5 = IS,
S.
Thus, the equation in the new system
is
Sx'2
+ ISy'2 = 72.
Dividing out the 72 puts this into the standard form
X,2
y,2
-+-
=1.
9 4
Linear
Algebra
Fig. Plot
ofthe
ellipse given by
13.x2
-
lOxy
+
By
- 72 = 0 and
,2
,2
the ellipse
x9
+
Y4
= 1 showing that the first ellipse is a
rotated version
of
the second ellipse
Now we can identify the ellipse in the new s}'§tem. We note that the given
ellipse
is
the new one rotated by some angle, which
we
still need to determine.
Next,
we
seek
the eigenvectors corresponding
to
each
eigenvalue.
Eigenvalue
1.
A =
S.
We insert the eigenvalue into the equation
(Q
-
Ai)v
=
O.
The system for the unknown eigenvector
is
(
13
-S
-5
)(VI)
=0.
-5
13-S
v2
The first equation is
5v
I
-
5v
2
= 0,
or
vI
= v
2
• Thus, we can choose our eigenvector to be
GJ=G}
Eigenvalue
2:
A = IS. In the same way, we insert the eigenvalue into the
equation
(Q
- Ai)v = 0 and obtain

Linear
Algebra
129
(13~518
13~18)(~)=O.
The first equation is
-5v
1
-
5v
2
=
0,
or
vI
=
-v
2
.
Thus, we can choose our eigenvector to be
(:J=(
~l).
We superimpose the eigenvectors on our original ellipse. We see that the
eigenvectors point in directions along the semimajor and semiminor axes and
indicate the angle
of
rotation. Eigenvector one is at a 45° angle. Thus, our
ellipse is a rotated version
of
one
in
standard position. Or, we could define
new axes that are at
45° to the standard axes and then the ellipse would take
the standard fonn in the new coordinate system. A general rotation
of
any
conic can be perfonned. Consider the general equation:
Ax2
+ 2Bxy +
cy2+
Ex
+ Fy = D.
We would like to find a rotation that puts it in the fonn
"'lx'2 +
~y'2
+
Ex'
+ F'y' =
D.
We use the rotation matrix
A =(COS9
-sin9)
Re
sin9 cos9
and define
x'
=
Rl
x,
or
x =
Rex'.
The general equation can be written in matrix fonn:
x
T
Qx+
fx
=D,
where Q is the usual matrix
of
coefficients A,
B,
and C and f = (E, F).
Transfonning this equation gives
x'T
k1e
QReX'+
fReX'
= D
The resulting equation is
of
the fonn
A'x'2 + 2B'x'y'+ C' y'2 +
Ex'
+
F'
y'
= D,
where
B'
= 2( C -
A)
sin9 cos9 + 2B(2 cos9
2
-
1).
If
we want the nonrotated fonn, then we seek an angle 9 such that
B' =
o.
Noting that 2 sin 9 cos 9 = sin29 and 2 cos 9
2
- 1 = cos 29, this gives
tan(29) =
A - C
A-C
tan(29)
=--.
B
So, in our previous example, with A = C =
13
and B =
-5,
we have tan(29)
=
00.
Thus, 29 = 7tl2,
or
9 = x/4:
Finally, we had noted that knowing the coefficients in the general quadratic
is enough to detennine the type
of
conic represented without doing any plotting.
130
Linear
Algebra
This is based on the fact that the determinant
of
the coefficient matrix is
invariant under rotation.
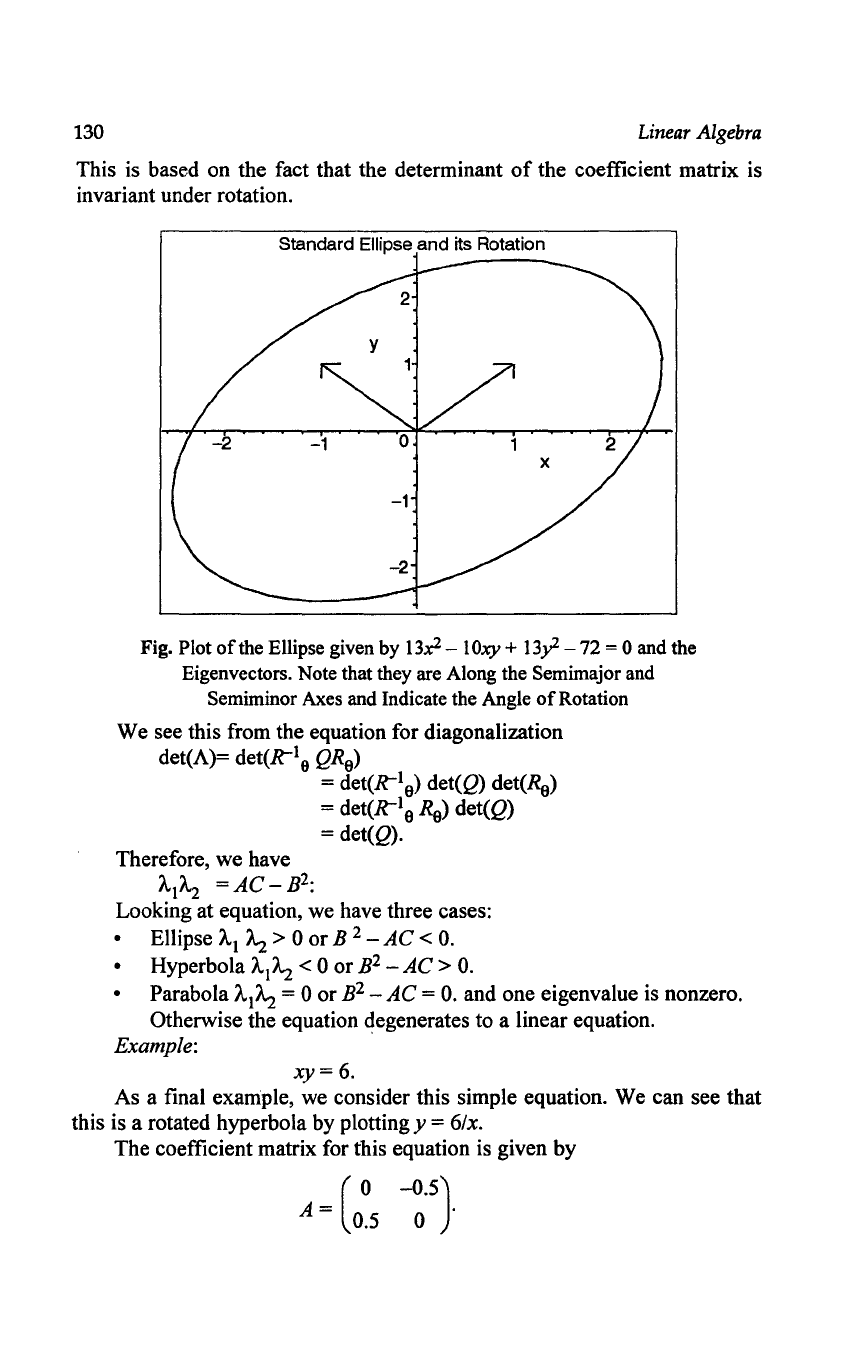
Standard Ellipse
and
its Rotation
Fig. Plot
of
the Ellipse given
by
13x2
- lOxy +
13y
-72 = 0 and the
Eigenvectors. Note that they are Along the Semimajor and
Semiminor Axes and Indicate the Angle
of
Rotation
We see this from the equation for diagonalization
det(A)=
det(JtI
e QRe)
=
det(JtI
e)
det(Q) det(R
e
)
=
det(JtI
e
Re)
det(Q)
= det(Q).
Therefore, we have
AIA2
=AC-B2:
Looking at equation, we have three cases:
• Ellipse
Al
~ > 0 or B 2 -
AC
<
O.
• Hyperbola
Al
~
< 0 or
B2
-
AC
>
O.
• Parabola
AI~
= 0 or
B2
-
AC
=
O.
and one eigenvalue is nonzero.
Otherwise the equation degenerates to a linear equation.
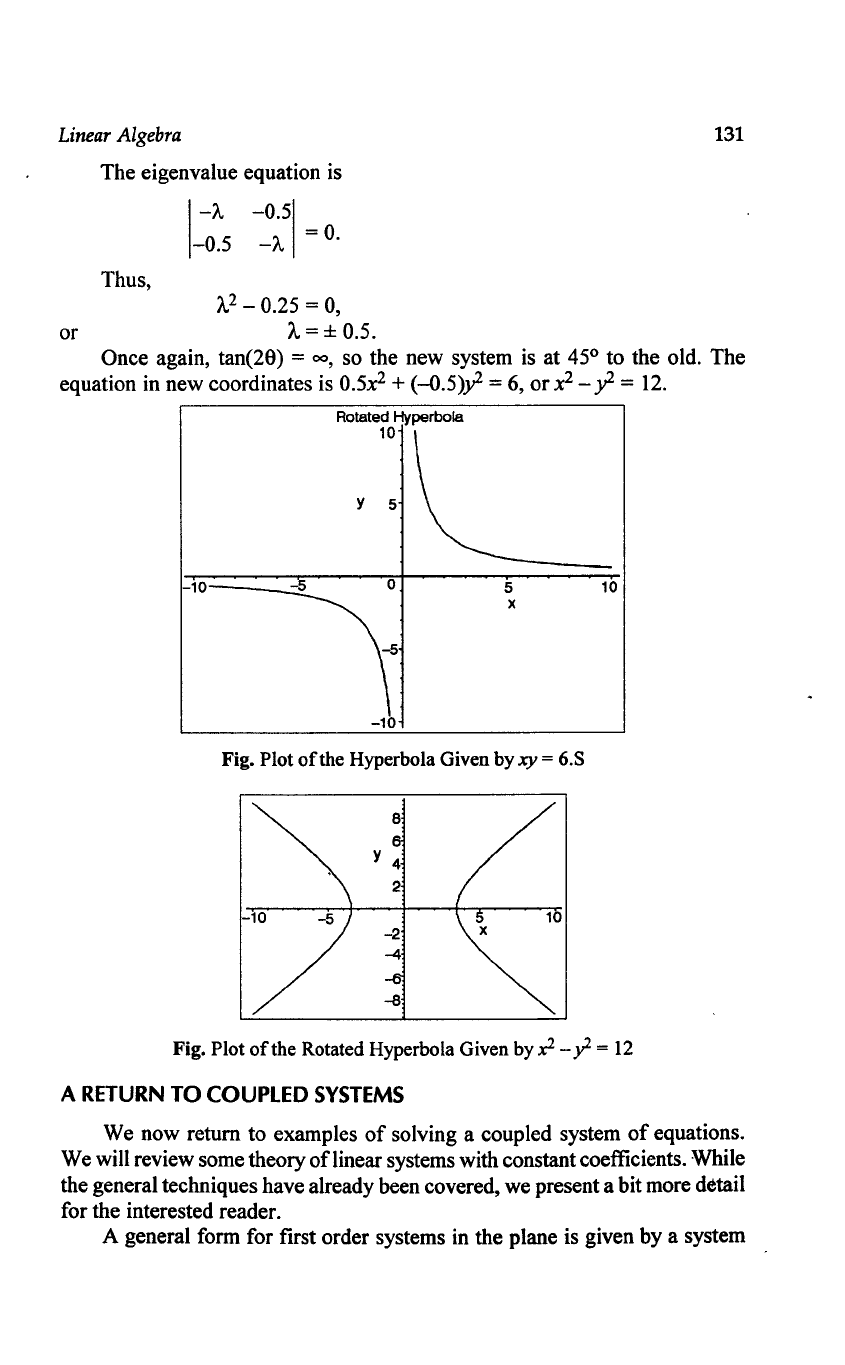
Example:
xy=6.
As a final example, we consider this simple equation. We can see that
this is a rotated hyperbola by plottingy =
6/x.
The coefficient matrix for this equation is given by
=
(0
-0.5).
A
0.5
0
Linear
Algebra
The eigenvalue equation is
Thus,
or
I
-A
-0.51
=
-0.5
-A
O.
')..2
_ 0.25 = 0,
')..=±0.5.
131
Once again, tan(29) = 00, so the new system is at 45° to the old. The
equation in new coordinates is
0.5.x2
+ (-O.5)y2 = 6, or.x2 -
y2
= 12.
Rotated Hyperbola
10
Y 5
-10---...:=-"
5
x
Fig. Plot
of
the Hyperbola Given by
xy
= 6.S
10
Fig. Plot
of
the Rotated Hyperbola Given by
x2
-
Y.
=
12
A
RETURN
TO
COUPLED
SYSTEMS
We now return to examples
of
solving a coupled system
of
equations.
We will review some theory
of
linear systems with constant coefficients. While
the general techniques have already been covered, we present a bit more detail
for the interested reader.
A general form for first order systems in the plane is given by a system
