Brewster H.D. Mathematical Physics
Подождите немного. Документ загружается.

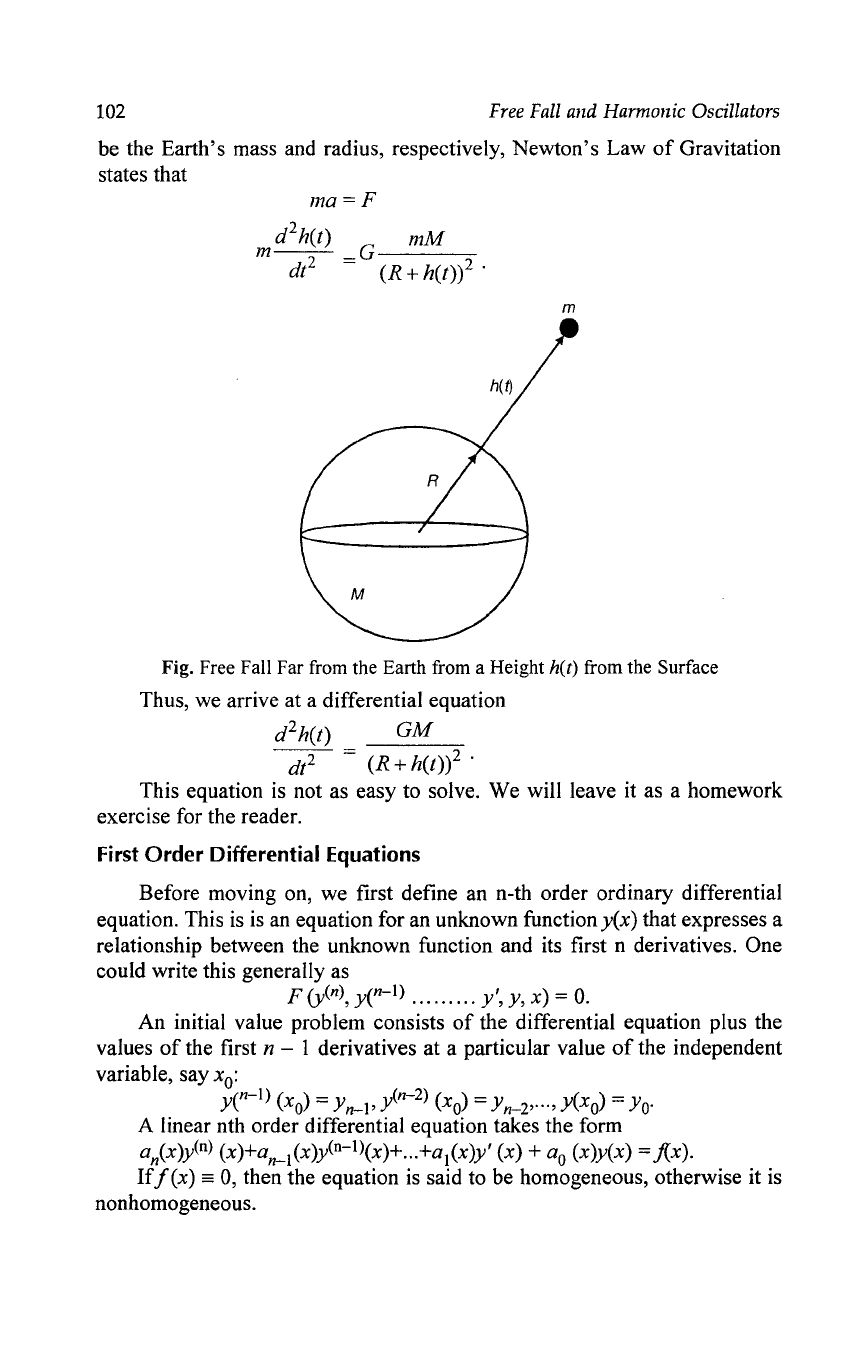
102
Free Fall alld Harmollic Oscillators
be the Earth's mass
and
radius, respectively, Newton's Law
of
Gravitation
states that
ma=F
d
2
h(t)
mM
m--
_
G----::--
dt
2
-
(R
+
h(t»2
.
m
Fig. Free Fall Far from the Earth from a Height h(t) from the Surface
Thus, we arrive at a differential equation
d
2
h(t)
GM
---:iT
= (R +
h(t»2
.
This equation
is
not as easy to solve. We will leave
it
as a homework
exercise for the reader.
First
Order
Differential Equations
Before moving on, we first define an n-th order ordinary differential
equation. This
is is
an
equation for an unknown
functiony(x)
that expresses a
relationship between the unknown function and its first n derivatives.
One
could write this generally
as
F
(y(n),
y(n-I)
.........
y',
y,
x)
=
0.
An initial value problem consists
of
the differential equation plus the
values
of
the first n - 1 derivatives at a particular value
of
the independent
variable, say
xo:
y(n-I) (xo) = Yn-I'
y(n-2)
(xo) = Yn-2'···' y(xo) =
Yo·
A linear nth order differential equation takes the form
an(x)y(n) (x)+an-l(x)y(n-l)(x)+
...
+a
l
(x)y' (x)
+
aD
(x)y(x) =
fix).
IfJex)
==
0,
then the equation
is
said to
be
homogeneous, otherwise it
is
nonhomogeneous.

Free
Fall
and
Harmonic
Oscillators
103
We
will return
to
these definitions as we explore a variety
of
examples.
However, we will start with the simplest
of
ordinary differential equations.
Typically, the first differential equations encountered are first order
equations. A first order differential equation takes the form
F (y', y,
x)
=
O.
There are two general forms for which one can formally obtain a solution.
The first is the separable case and the second
is
a linear first order equation.
We indicate that we can formally obtain solutions, as one can indicate the
needed integration that leads to a solution. However, these integrals are not
always reducible to elementary functions nor does one necessarily obtain
explicit solutions when the integrals are doable.
A first order equation is separable
if
it can be written the form
dy
dx =
J(x)g(y).
Special cases result when
eitherJ(x)
= 1 or g(y) =
1.
In the first case the
equation is said to be autonomous.
The general solution to equation
is
obtained
in
terms
of
two integrals:
fg~:)
=
fJ(x)dx+C,
where C
is
an integration constant. This yields a family
of
solutions to the
differential equation corresponding to different values
of
C.
If
one can solve
equation for
y(x), then one obtains an explicit solution. Otherwise, one has a
family
of
implicit solutions.
If
an initial condition is given as well, then one
might be able to find a member
of
the family that satisfies this condition, which
is often called a particular solution.
Example:
y'
= 2xy,
yeO)
= 2.
Applying, one has
f;
= f
2xdx
+
C
.
Integrating yields
In
lYl
=
:xl
+
C.
Exponentiating, one obtains the general solution,
y(x) =
eX
2
+
C
=
AeX
2
,
where A = e
C
.
(Note that since C is arbitrary, then so is e
C
.
Thus, there is no loss in
generality using A instead
of
e
C
.).
Next, one seeks a particular solution
satisfying the initial condition. For
yeO)
=
2,
one finds that A =
2.
So, the
particular solution is
y(x) =
2eX
2
.
Example:
Y.Y'
=
-x.

104
Free
Fall
and
Harmonic
Oscillators
Following the same procedure as in the last example, one obtains.
fydy
=-
f
xdx
+
C
=>
i
=_x
2
+A,
where A = 2e.
Thus,
we
obtain
an
implicit
solution.
Writing
the
solution
as
xl +
y2
= A, we see that this
is
a family
of
circles for A > 0 and the origin
for
A =
O.
Thesecond type
of
first order equation encountered
is
the linear
first order differential equation
in
the form
Yo
(x) + p(x)y(x) = q(x).
In
this case one seeks an integrating factor, flex), which
is
a function that
one can multiply through the equation making the left side a perfect derivative.
Multiplying the equation by
fl, the resulting equation becomes
d
dx (flY) = flq·
The integrating factor that works
is
fleX)
= exp(fp(x)dx). The resulting
equation
is
then easily integrated to obtain
y(x)
=_1_[
fX
~l(S)q(S)dS
+
c].
flex)
Example:
xy'
+ y = x, x > 0
y(l)
=
o.
One first notes that this
is
a linear first order differential equation. Solving
for
y', one can see that it
is
not separable. However, it
is
not in the standard
form. So, we first rewrite the equation as
dyl
-+-y
=
1.
dx x
Next, we determine the integrating factor
[
f
x dS]
Inx
fl (x) = exp
~
= e = x .
MUltiplying equation by the flex) =
x,
we actually get back the original
equation! In this case we have found
thatxy'+
y must have been the derivative
of
something to start. In fact,
or
(xy) , =
xy'
+
x.
Therefore, equation becomes
(xy)' =
x.
Integrating one obtains
1 2
xy=
-x
+,C
2 '
1
Inserting this solution into the initial condition, 0 =
'2
+ C.

Free
Fall
and
Harmonic
Oscillators
105
1
Therefore, C =
-2"
. Thus, the solution
ofthe
initial value problem
is
y(x)
=
~(x-~).
There are other first order equations that one can solve for closed form
solutions. However, many equations are not solvable, or one
is
simply
interested
in
the behaviour
of
solutions.
In
such cases one turns to direction
fields.
Terminal Velocity
Now let's return to free fall. What
if
there
is
air resistance? We first need
to model the air resistance. As an object falls faster and faster, the drag force
becomes greater. So, this resistive force
is
a function
of
the velocity. There
are a couple
of
standard models that people use to test this. The idea
is
to
write
F =
ma
in
the form
mji =
-111g
+
l(v),
where 1 (v) gives the resistive force and mg
is
the weight. Recall that this
applies to free
fall near the Earth's surface. Also, for
it
to be
resistive,j(v)
should oppose the motion.
If
the body
is
falling,
then/(v)
should be positive.
Ifit
is
rising,
then/(v)
would have to be negative to indicate the opposition to
the motion.
On common determination derives from the drag force on an object
moving through a fluid. This force
is
given by
I 2
j{v)
=2"CA
p
v ,
where C
is
the drag coefficient, A is the cross sectional area and p
is
the fluid
density. For laminar flow the drag coefficient
is
constant.
Unless you are into aerodynamics, you do not need to get into the details
of
the constants. So, it
is
best to absorb all
of
the constants into one to simplify
the computation. So, we will write
/ (v) = bv
2
.
Our equation can then be
rewritten as
. - kv
2
v -
-g,
where k = blm. Note that this
is
a first order equation for v(l). It
is
separable
too!
Formally, we can separate the variables and integrate the time out to obtain
f
dz
t +
K=
kz2
.
-g
(Note. We used an integration constant
ofK
since C
is
the drag coefficient
in
this problem.)
Ifwe
can do the integral, then we have a solution for
v.

106
Free
Fall
and
Harmonic
Oscillators
In
fact, we can do this integral. You need to recall another common method
of
integration, which we have not reviewed yet. Do you remember Partial
Fraction Decomposition?
It
involves factoring the denominator in our integral.
Of
course, this
is
ugly because our constants are represented by letters and are
not specific numbers. Letting a
2
= g/k, we can write the integrand as
kz2
- g = k
z2
~
a
2
=
2~k
[z
~
a - z
~
a].
Now, the integrand can be easily integrated giving
1
Iv-al
t+K=--ln
--
.
2ak
v+a
Solving for
v,
we have
1_Ae
2akt
vet) =
2akt
a ,
>
l+Ae
where A
==
e
K
.
A can be determined using the initial velocity.
There are other forms for the solution in terms
of
a tanh function, which
the reader can determine as an exercise.
One important conclusion is that for
large times, the ratio
in
the solution approaches
-1.
Thus, v
~
- a = -
Jf
. This means that the falling object will reach a
terminal velocity.
As a simple computation, we can determine the terminal velocity. We
will take an
80 kg skydiver with a cross sectional area
of
about 0.093 m
2
.
(The skydiver is falling head first.) Assume that the air density is a constant
1.2 kgim
3
and the drag coefficient is C = 2.0. We first note that
Vterminal
=-Jf
=
-1~~~
.
So,
Vterminal =
2(70)(9.8) =
78m/
s
(2.0)(0.093)(1.2)
This is about 175 mph, which is slightly higher than the actual terminal
velocity
of
a sky diver. One would need a more accurate determination
ofC.

Chapter
4
Linear
Algebra
Calculus has its roots in physics and has become a very useful tool for
modelling the physical world. Another very important area
of
mathematics is
linear algebra.
VECTOR
SPACES
Much
of
the discussion and terminology that we will use comes from the
theory
of
vector spaces. Until now you may only have dealt with finite
dimensional vector spaces.
Even then, you might only be comfortable with vectors
in
two and three
dimensions. We will review a little
of
what we know about finite dimensional
vector spaces.
The notion
of
a vector space
is
a generalization
of
the three dimensional
vector spaces that you have seen in introductory physics and calculus. In three
dimensions, we have objects called vectors, which you first visualized as arrows
of
a specific length and pointing in a given direction. To each vector, we can
associate a point in a three dimensional Cartesian system. We
just
attach the
tail
of
the vector v to the origin and the head lands
at
some point, (x, y, z). We
then used the unit vectors
i, j and k along the coordinate axes to write the
vector in the form
v =
xi
+
yj
+ zk.
Having defined vectors, we then learned how to add vectors and multiply
vectors by numbers,
or
scalars.
Under these operations, we expected to get back new vectors. Then we
learned that there were two types
of
multiplication
of
vectors. We could
mUltiply two vectors
to get either a scalar or a vector. This lead to the operations
of
dot and cross products, respectively.
The dot product was useful for determining the length
of
a vector, the
angle between two vectors, or
if
the vectors were orthogonal.
In physics you first learned about vector products when you defined work,
W = F .
r.
Cross products were useful
in
describing things like torque,
't
= r x
F,
or
the force on a moving charge
in
a magnetic field, F = qv x
B.
We will
return to these more complicated vector operations later when reviewing

108 Linear Algebra
Maxwell's equations
of
electrodyn-amics.
The
basic concept
of
a vector
can be generalized
to
spaces
of
more
than
three dimensions.
You
may first have seen this in your linear algebra class. The properties
outlined roughly above need
to
be preserved.
So,
we
have to
start
with a space
of
vectors
and
the
operations between
them. We also need a set
of
scalars, which generally come from some field.
However, in
our
applications the field
will
either be the set
of
real numbers
or
the set
of
complex numbers.
A vector space Vover a field
Fis a set
that
is
closed under addition
and
scalar multiplication and satisfies the following conditions:
For
any
u,
v,
IV E V
and
a,
bE
F
• u + v = v + U.
• (u + v) + w = u + (v +
IV).
• There exists a 0 such
that
0 + v =
v.
• There exists a
-v
such
that
v +
(-v)
=
0:
• a(bv) = (ab)v.
(a
+ b)v = av + bv.
•
a(u
+ v) =
au
+ bv.
•
l(v)=v.
In three dimensions the unit vectors
i,j
and
k play
an
important role. Any
vector in
the
three dimensional space can be written as a linear combination
of
these vectors,
v
=xi+yj+zk.
In fact, given any three non-coplanar vectors,fa
(,
a
2
,
a:,f5,
all vectors can
be written as a linear combination
of
those vectors,
v = c(a( + c
2
a( + c
3
a(.
Such vectors are said
to
span
the
space
and
are called a basis for
the
space. We can generalize these ideas.
In
an
n-dimensional vector space any
vector in the space can be represented as the sum over n linearly independent
vectors (the equivalent
of
non-coplanar vectors). Such a linearly independent
set
of
vectors
{Vj
}
~=1
satisfies the condition
n
ICjVj
=0
<=>
Cj
=0
j=l
Note
that
we
will
often use summation notation instead
of
writing
out
all
of
the terms in the sum.
The
standard
basis in
an
n-dimensional vector space
is
a generalization
ofthe
standard
basis in three dimensions
(i,j
and
k). We define

Linear
Algebra
ek
=
(0,
..
,0,
..2-,
,0,
..
,0),k = I,··,n.
kth
space
Then,
we
can
expand
any v E Vas
n
l'
=Lukek>
k=I
where the
l'k'S
are called
the
components
of
the
vector in this basis.
109
Sometimes we will write v as
an
n-tuple
(vI'
v
2
' ... ,v
n
).
This
is
similar
to
the
ambiguous use
of
(x,
y,
z)
to
denote
both
vectors in as well as
to
represent
points in the three dimensional space.
The
only
other
thing
we will need
at
this
point
is
to
generalize
the
dot
product. Recall that there are two forms for the dot product
in
three dimensions.
First, one has that
U . v =
uv
cos
e,
where U and v denote the length
of
the vectors. The other form
is
the component
form:
3
u·
v = uIv
I
+ u
2
v
2
+ u
3
v
3
= LUkUk·
k=I
Of
course, this form
is
easier to generalize. So,
we
define the scalar product
between two n-dimensional vectors as
3
< u,v > = LUkUk·
k=I
,Actually,
there
are
a
number
of
notations
that
are
used in
other
texts.
One
can write the scalar product as
(u,
v)
or
even in the Dirac bra-ket notation
<ulv>.
We note
that
the
(real) scalar
product
satisfies
some
simple properties.
For
vectors
v,
wand
real scalar a
we
have
• <
v,
v
>~
°
and
<
v,
v > = 0 if
and
only
if
v =
O.
•
<v,w>=<w,v>.
• <
(l
v,
W > =
a.
<
v,
w
>.
While it does
not
always make sense
to
talk about angles between general
vectors in higher dimensional vector spaces, there
is
one concept
that
is
useful.
It
is
that
of
orthogonality, which in three dimensions
is
another way
of
saying
the vectors are perpendicular
to
each other. So, we also say
that
vectors U
and
v are orthogonal if
and
only
if
<
u,
v
>=
O.
If
{ak}
k=I,
is
a set
of
basis vectors
such that
<apa,,>=O,k*J,
then it
is
called
an
orthogonal basis.
If
in
addition
each basis vector
is
a
unit
vector,
then
one
has
an
orthonormal basis. This generalization
of
the unit basis can be expressed more

110 Linear Algebra
compactly.
We
will
denote
such
a
basis
of
unit
vectors
by
e
j
for
j = 1
...
n.
Then,
<
e
p
e k > = 0 k'
where we have introduced the Kronecker delta
{
O,
}::f::-k
O;k
==
1,
} = k
The
process
of
making
basis
vectors
have
unit
length
is
called
normalization. This
is
simply done by dividing by the length
of
the vector.
Recall that the length
ofa
vector,
v,
is obtained as v
=~.
So,
if
we want to
find a unit vector in the direction
of
v,
then we simply normalize it as
v
v=
-.
u
Notice
that
we used a
hat
to indicate
that
we have a
unit
vector.
FUl1hermore,
if{aj
}J=l, is a set
of
orthogonal basis vectors, then
a,
. 1
e
j
=
~<
aj,a;
>
,j
= ...
n.
Let{adk=l'
be a set
of
011hogonal basis vectors for vector space
V.
We
know
that
any
vector
v
can
be
represented
in
terms
of
this
basis,
v =
I;=l
ukak
Ifwe
know the basis and vector, can we find the components?
The answer
is
yes. We can use the scalar product
ofv
with each basis element
aj"
Using the properties
of
the scalar product, we have for} =
1,
... , n
and
n
< a.,
v>
=
<aj,IUkak
>
;
k=l
n
=
IUk
<aj,ak
>.
k=l
Since we know the basis elements, we can easily compute the numbers
Ajk
==
<
aJ'
a
k
>
b
j
==
<
aj'
v >.
Therefore, the system for the vk's is a linear algebraic system, which takes
the form

Linear Algebra
111
We can write this set
of
equations in a more compact form. The set
of
numbers A 'k,j, k = I,
...
n are the elements
of
an n x n matrix A with
Alk
being
an
element
in
the
jth
row and kth column. Also, Vj and h
J
can be written as
column vectors,
v and
h,
respectively. Thus, system can be written
in
matrix
form as
Av=
h.
However, if the basis
is
orthogonal, then the matrix A
Jk
==
< aJ' a
k
>
is
diagonal and the system
is
easily solvable. Recall that two vectors are
orthogonal
if
and only
if
< ai' {1j> = 0, i
*-
j.
Thus,
in
this case we have that
< a
j
,
v>
=
'}
<
(~,
a
J
>,j
=
1,
...
,11.
or
V·=
J
<aj,a
j
>
In
fact,
if
the basis
is
orthonormal, i.e., the basis consists
of
an
olthogonal
set
of
unit vectors, then A
is
the identity matrix and the solution takes on a
simpler form:
v
=<a
v>
J
J'
y
(x.
y)
x
Fig. Vector v
in
a standard coordinate system.
LINEAR
TRANSFORMATIONS
A main theme
in
linear algebra
is
to study linear transformations between
vector spaces. These come
in
many forms and there are an abundance
of
applications
in
physics. For example, the transformation between the spacetime
coordinates
of
observers moving
in
inertial frames
in
th~
theory
of
special
relativity constitute such a transformation.
A simple example often encountered
in
physics courses
is
the rotation by
a fixed angle. This
is
the description
of
points
in
space using two different
coordinate bases, one
just
a rotation
of
the other by some angle. We begin
