Brennen Ch.E. Fundamentals of Multiphase Flow
Подождите немного. Документ загружается.


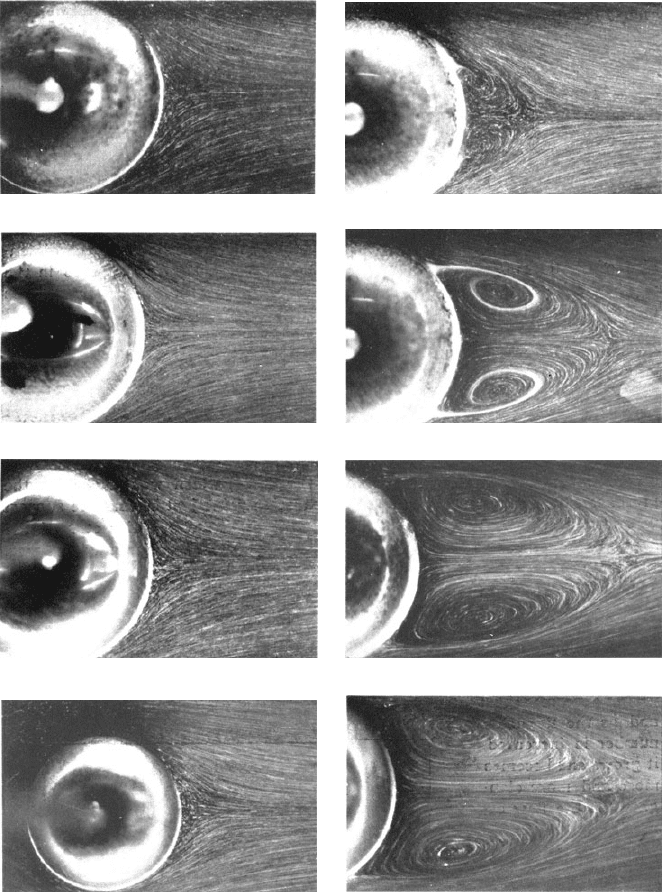
lutions are numerous. Experimentally, it is found that a recirculating zone
(or vortex ring) develops close to the rear stagnation point at about Re =30
(see Taneda 1956 and figure 2.4). With further increase in the Reynolds
number this recirculating zone or wake expands. Defining locations on the
surface by the angle from the front stagnation point, the separation point
moves forward from about 130
◦
at Re = 100 to about 115
◦
at Re = 300. In
the process the wake reaches a diameter comparable to that of the sphere
when Re ≈ 130. At this point the flow becomes unstable and the ring vor-
tex that makes up the wake begins to oscillate (Taneda 1956). However, it
continues to be attached to the sphere until about Re = 500 (Torobin and
Gauvin 1959).
At Reynolds numbers above about 500, vortices begin to be shed and
then convected downstream. The frequency of vortex shedding has not been
studied as extensively as in the case of a circular cylinder and seems to vary
more with Reynolds number. In terms of the conventional Strouhal number,
Str, defined as
Str =2fR/W (2.22)
the vortex shedding frequencies, f, that Moller (1938) observed correspond
to a range of Str varying from 0.3atRe = 1000 to about 1.8atRe = 5000.
Furthermore, as Re increases above 500 the flow develops a fairly steady
near-wake behind which vortex shedding forms an unsteady and increasingly
turbulent far-wake. This process continues until, at a value of Re of the order
of 1000, the flow around the sphere and in the near-wake again becomes
quite steady. A recognizable boundary layer has developed on the front of
the sphere and separation settles down to a position about 84
◦
from the
front stagnation point. Transition to turbulence occurs on the free shear
layer (which defines the boundary of the near-wake) and moves progressively
forward as the Reynolds number increases. The flow is similar to that of the
top picture in figure 2.2. Then the events described in the previous section
occur with further increase in the Reynolds number.
Since the Reynolds number range between 0.5 and several hundred can
often pertain in multiphase flows, one must resort to an empirical formula
for the drag force in this regime. A number of empirical results are available;
for example, Klyachko (1934) recommends
F
1
= −6πρ
C
ν
C
WR
1+
Re
2
3
6
(2.23)
which fits the data fairly well up to Re ≈ 1000. At Re = 1 the factor in the
59
Re =9.15 Re =37.7
Re =17.9 Re =73.6
Re =25.5 Re = 118
Re =26.8 Re = 133
Figure 2.4. Streamlines of steady flow (from left to right) past a sphere at
various Reynolds numbers (from Taneda 1956, reproduced by permission
of the author).
60

square brackets is 1.167, whereas the same factor in equation 2.20 is 1.187.
On the other hand, at Re = 1000, the two factors are respectively 17.7and
188.5.
2.2.3 Molecular effects
When the mean free path of the molecules in the surrounding fluid, λ,be-
comes comparable with the size of the particles, the flow will clearly deviate
from the continuum models, that are only relevant when λ R. The Knud-
sen number, Kn = λ/2R, is used to characterize these circumstances, and
Cunningham (1910) showed that the first-order correction for small but finite
Knudsen number leads to an additional factor, (1 + 2AKn), in the Stokes
drag for a spherical particle. The numerical factor, A, is roughly a constant
of order unity (see, for example, Green and Lane 1964).
When the impulse generated by the collision of a single fluid molecule
with the particle is large enough to cause significant change in the particle
velocity, the resulting random motions of the particle are called Brownian
motion (Einstein 1956). This leads to diffusion of solid particles suspended
in a fluid. Einstein showed that the diffusivity, D, of this process is given by
D = kT/6πµ
C
R (2.24)
where k is Boltzmann’s constant. It follows that the typical rms displace-
ment of the particle in a time, t,isgivenby(kTt/3πµ
C
R)
1
2
.Brownian
motion is usually only significant for micron- and sub-micron-sized parti-
cles. The example quoted by Einstein is that of a 1 µm diameter particle
in water at 17
◦
C for which the typical displacement during one second is
0.8 µm.
A third, related phenomenon is the response of a particle to the collisions
of molecules when there is a significant temperature gradient in the fluid.
Then the impulses imparted to the particle by molecular collisions on the
hot side of the particle will be larger than the impulses on the cold side. The
particle will therefore experience a net force driving it in the direction of the
colder fluid. This phenomenon is known as thermophoresis (see, for example,
Davies 1966). A similar phenomenon known as photophoresis occurs when
a particle is subjected to nonuniform radiation. One could include in this
list the Bjerknes forces described in the section 3.4 since they constitute
sonophoresis, namely forces acting on a particle in a sound field.
61

2.3 UNSTEADY EFFECTS
2.3.1 Unsteady particle motions
Having reviewed the steady motion of a particle relative to a fluid, we must
now consider the consequences of unsteady relative motion in which either
the particle or the fluid or both are accelerating. The complexities of fluid
acceleration are delayed until the next section. First we shall consider the
simpler circumstance in which the fluid is either at rest or has a steady
uniform streaming motion (U = constant) far from the particle. Clearly the
second case is readily reduced to the first by a simple Galilean transformation
and it will be assumed that this has been accomplished.
In the ideal case of unsteady inviscid potential flow, it can then be shown
by using the concept of the total kinetic energy of the fluid that the force
on a rigid particle in an incompressible flow is given by F
i
,where
F
i
= −M
ij
dV
j
dt
(2.25)
where M
ij
is called the added mass matrix (or tensor) though the name
induced inertia tensor used by Batchelor (1967) is, perhaps, more descrip-
tive. The reader is referred to Sarpkaya and Isaacson (1981), Yih (1969), or
Batchelor (1967) for detailed descriptions of such analyses. The above men-
tioned methods also show that M
ij
for any finite particle can be obtained
from knowledge of several steady potential flows. In fact,
M
ij
=
ρ
C
2
volume
of f luid
u
ik
u
jk
d(volume) (2.26)
where the integration is performed over the entire volume of the fluid. The
velocity field, u
ij
, is the fluid velocity in the i direction caused by the steady
translation of the particle with unit velocity in the j direction. Note that
this means that M
ij
is necessarily a symmetric matrix. Furthermore, it is
clear that particles with planes of symmetry will not experience a force
perpendicular to that plane when the direction of acceleration is parallel to
that plane. Hence if there is a plane of symmetry perpendicular to the k
direction, then for i = k, M
ki
= M
ik
= 0, and the only off-diagonal matrix
elements that can be nonzero are M
ij
, j = k, i = k. In the special case of
the sphere all the off-diagonal terms will be zero.
Tables of some available values of the diagonal components of M
ij
are
given by Sarpkaya and Isaacson (1981) who also summarize the experi-
mental results, particularly for planar flows past cylinders. Other compila-
tions of added mass results can be found in Kennard (1967), Patton (1965),
62
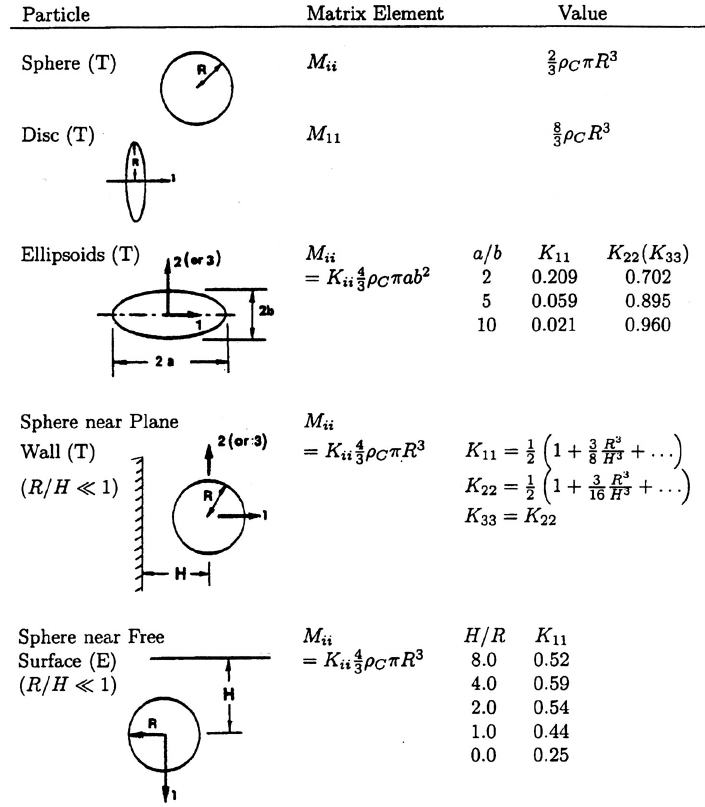
Table 2.1. Added masses (diagonal terms in M
ij
) for some three-dimensional
bodies (particles): (T) Potential flow calculations, (E) Experimental data
from Patton (1965).
and Brennen (1982). Some typical values for three-dimensional particles are
listed in Table 2.1. The uniform diagonal value for a sphere (often referred to
simply as the added mass of a sphere) is 2ρ
C
πR
3
/3 or one-half the displaced
mass of fluid. This value can readily be obtained from equation 2.26 using
the steady flow results given in equations 2.7 to 2.10. In general, of course,
there is no special relation between the added mass and the displaced mass.
63

Consider, for example, the case of the infinitely thin plate or disc with zero
displaced mass which has a finite added mass in the direction normal to the
surface. Finally, it should be noted that the literature contains little, if any,
information on off-diagonal components of added mass matrices.
Now consider the application of these potential flow results to real viscous
flows at high Reynolds numbers (the case of low Reynolds number flows will
be discussed in section 2.3.4). Significant doubts about the applicability of
the added masses calculated from potential flow analysis would be justified
because of the experience of D’Alembert’s paradox for steady potential flows
and the substantial difference between the streamlines of the potential and
actual flows. Furthermore, analyses of experimental results will require the
separation of the added mass forces from the viscous drag forces. Usually
this is accomplished by heuristic summation of the two forces so that
F
i
= −M
ij
dV
j
dt
−
1
2
ρ
C
AC
ij
|V
j
|V
j
(2.27)
where C
ij
is a lift and drag coefficient matrix and A is a typical cross-
sectional area for the body. This is known as Morison’s equation (see Morison
et al. 1950).
Actual unsteady high Reynolds number flows are more complicated and
not necessarily compatible with such simple superposition. This is reflected
in the fact that the coefficients, M
ij
and C
ij
, appear from the experimental
results to be not only functions of Re but also functions of the reduced
time or frequency of the unsteady motion. Typically experiments involve
either oscillation of a body in a fluid or acceleration from rest. The most
extensively studied case involves planar flow past a cylinder (for example,
Keulegan and Carpenter 1958), and a detailed review of this data is included
in Sarpkaya and Isaacson (1981). For oscillatory motion of the cylinder with
velocity amplitude, U
M
,andperiod,t
∗
, the coefficients are functions of both
the Reynolds number, Re =2U
M
R/ν
C
, and the reduced period or Keulegan-
Carpenter number, Kc = U
M
t
∗
/2R. When the amplitude, U
M
t
∗
,islessthan
about 10R (Kc < 5), the inertial effects dominate and M
ii
is only a little less
than its potential flow value over a wide range of Reynolds numbers (10
4
<
Re < 10
6
). However, for larger values of Kc, M
ii
can be substantially smaller
than this and, in some range of Re and Kc, may actually be negative. The
values of C
ii
(the drag coefficient) that are deduced from experiments are
also a complicated function of Re and Kc. The behavior of the coefficients
is particularly pathological when the reduced period, Kc, is close to that of
vortex shedding (Kc of the order of 10). Large transverse or lift forces can be
generated under these circumstances. To the author’s knowledge, detailed
64

investigations of this kind have not been made for a spherical body, but one
might expect the same qualitative phenomena to occur.
2.3.2 Effect of concentration on added mass
Though most multiphase flow effects are delayed until later chapters it is
convenient at this point to address the issue of the effect on the added mass
of the particles in the surrounding mixture. It is to be expected that the
added mass coefficient for an individual particle would depend on the void
fraction of the surrounding medium. Zuber (1964) first addressed this issue
using a cell method and found that the added mass, M
ii
, for spherical bubbles
increased with volume fraction, α, like
M
ii
(α)
M
ii
(0)
=
(1 + 2α)
(1 − α)
=1+3α + O(α
2
) (2.28)
The simplistic geometry assumed in the cell method (a concentric spheri-
cal shell of fluid surrounding each spherical particle) caused later researchers
to attempt improvements to Zuber’s analysis; for example, van Wijngaarden
(1976) used an improved geometry (and the assumption of potential flow)
to study the O(α) term and found that
M
ii
(α)
M
ii
(0)
=1+2.76α + O(α
2
) (2.29)
which is close to Zuber’s result. However, even more accurate and more
recent analyses by Sangani et al. (1991) have shown that Zuber’s original
result is, in fact, remarkably accurate even up to volume fractions as large
as 50% (see also Zhang and Prosperetti 1994).
2.3.3 Unsteady potential flow
In general, a particle moving in any flow other than a steady uniform stream
will experience fluid accelerations, and it is therefore necessary to consider
the structure of the equation governing the particle motion under these
circumstances. Of course, this will include the special case of acceleration of
a particle in a fluid at rest (or with a steady streaming motion). As in the
earlier sections we shall confine the detailed solutions to those for a spherical
particle or bubble. Furthermore, we consider only those circumstances in
which both the particle and fluid acceleration are in one direction, chosen
for convenience to be the x
1
direction. The effect of an external force field
65

such as gravity will be omitted; it can readily be inserted into any of the
solutions that follow by the addition of the conventional buoyancy force.
All the solutions discussed are obtained in an accelerating frame of refer-
ence fixed in the center of the fluid particle. Therefore, if the velocity of the
particle in some original, noninertial coordinate system, x
∗
i
,wasV (t)inthe
x
∗
1
direction, the Navier-Stokes equations in the new frame, x
i
,fixedinthe
particle center are
∂u
i
∂t
+ u
j
∂u
i
∂x
j
= −
1
ρ
C
∂P
∂x
i
+ ν
C
∂
2
u
i
∂x
j
∂x
j
(2.30)
where the pseudo-pressure, P , is related to the actual pressure, p,by
P = p + ρ
C
x
1
dV
dt
(2.31)
Here the conventional time derivative of V (t) is denoted by d/dt, but it
should be noted that in the original x
∗
i
frame it implies a Lagrangian deriva-
tive following the particle. As before, the fluid is assumed incompressible
(so that continuity requires ∂u
i
/∂x
i
= 0) and Newtonian. The velocity that
the fluid would have at the x
i
origin in the absence of the particle is then
W (t)inthex
1
direction. It is also convenient to define the quantities r, θ,
u
r
, u
θ
as shown in figure 2.1 and the Stokes streamfunction as in equations
2.6. In some cases we shall also be able to consider the unsteady effects due
to growth of the bubble so the radius is denoted by R(t).
First consider inviscid potential flow for which equations 2.30 may be
integrated to obtain the Bernoulli equation
∂φ
∂t
+
P
ρ
C
+
1
2
(u
2
θ
+ u
2
r
)=constant (2.32)
where φ is a velocity potential (u
i
= ∂φ/∂x
i
)andψ must satisfy the equation
Lψ =0 where L ≡
∂
2
∂r
2
+
sin θ
r
2
∂
∂θ
1
sin θ
∂
∂θ
(2.33)
This is of course the same equation as in steady flow and has harmonic
solutions, only five of which are necessary for present purposes:
ψ =sin
2
θ
−
Wr
2
2
+
D
r
+cosθ sin
2
θ
2Ar
3
3
−
B
r
2
+ E cos θ (2.34)
φ =cosθ
−Wr +
D
r
2
+(cos
2
θ −
1
3
)
Ar
2
+
B
r
3
+
E
r
(2.35)
66
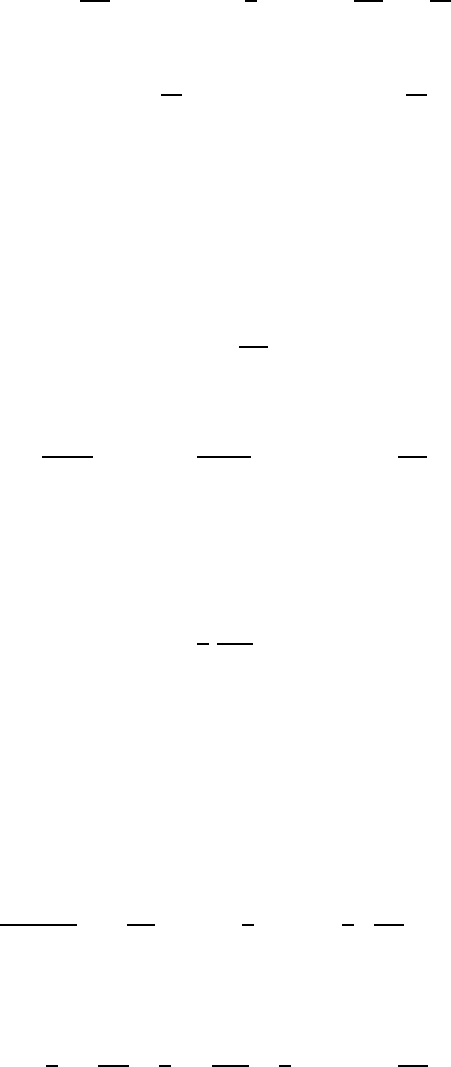
u
r
=cosθ
−W −
2D
r
3
+(cos
2
θ −
1
3
)
2Ar −
3B
r
4
−
E
r
2
(2.36)
u
θ
= − sin θ
−W +
D
r
3
− 2cosθ sin θ
Ar +
B
r
4
(2.37)
The first part, which involves W and D, is identical to that for steady
translation. The second, involving A and B, will provide the fluid velocity
gradient in the x
1
direction, and the third, involving E, permits a time-
dependent particle (bubble) radius. The W and A terms represent the fluid
flow in the absence of the particle, and the D, B, and E terms allow the
boundary condition
(u
r
)
r=R
=
dR
dt
(2.38)
to be satisfied provided
D = −
WR
3
2
,B=
2AR
5
3
,E= −R
2
dR
dt
(2.39)
In the absence of the particle the velocity of the fluid at the origin, r =0,is
simply −W in the x
1
direction and the gradient of the velocity ∂u
1
/∂x
1
=
4A/3. Hence A is determined from the fluid velocity gradient in the original
frame as
A =
3
4
∂U
∂x
∗
1
(2.40)
Now the force, F
1
, on the bubble in the x
1
direction is given by
F
1
= −2πR
2
π
0
p sin θ cos θdθ (2.41)
which upon using equations 2.31, 2.32, and 2.35 to 2.37 can be integrated
to yield
F
1
2πR
2
ρ
C
= −
D
Dt
(WR) −
4
3
RWA +
2
3
R
dV
dt
(2.42)
Reverting to the original coordinate system and using v as the sphere volume
for convenience (v =4πR
3
/3), one obtains
F
1
= −
1
2
ρ
C
v
dV
dt
∗
+
3
2
ρ
C
v
DU
Dt
∗
+
1
2
ρ
C
(U − V )
dv
dt
∗
(2.43)
67

where the two Lagrangian time derivatives are defined by
D
Dt
∗
≡
∂
∂t
∗
+ U
∂
∂x
∗
1
(2.44)
d
dt
∗
≡
∂
∂t
∗
+ V
∂
∂x
∗
1
(2.45)
Equation 2.43 is an important result, and care must be taken not to confuse
the different time derivatives contained in it. Note that in the absence of
bubble growth, of viscous drag, and of body forces, the equation of motion
that results from setting F
1
=0is
1+
2m
p
ρ
C
v
dV
dt
∗
=3
DU
Dt
∗
(2.46)
where m
p
is the mass of the particle. Thus for a massless bubble the accel-
eration of the bubble is three times the fluid acceleration.
In a more comprehensive study of unsteady potential flows Symington
(1978) has shown that the result for more general (i.e., noncolinear) accel-
erations of the fluid and particle is merely the vector equivalent of equation
2.43:
F
i
= −
1
2
ρ
C
v
dV
i
dt
∗
+
3
2
ρ
C
v
DU
i
Dt
∗
+
1
2
ρ
C
(U
i
− V
i
)
dv
dt
∗
(2.47)
where
d
dt
∗
=
∂
∂t
∗
+ V
j
∂
∂x
∗
j
;
D
Dt
∗
=
∂
∂t
∗
+ U
j
∂
∂x
∗
j
(2.48)
The first term in equation 2.47 represents the conventional added mass effect
due to the particle acceleration. The factor 3/2 in the second term due to
the fluid acceleration may initially seem surprising. However, it is made up
of two components:
1.
1
2
ρ
C
dV
i
/dt
∗
, which is the added mass effect of the fluid acceleration
2. ρ
C
vDU
i
/Dt
∗
,whichisabuoyancy-like force due to the pressure gradient asso-
ciated with the fluid acceleration.
The last term in equation 2.47 is caused by particle (bubble) volumetric
growth, dv/dt
∗
, and is similar in form to the force on a source in a uniform
stream.
Now it is necessary to ask how this force given by equation 2.47 should
be used in the practical construction of an equation of motion for a particle.
Frequently, a viscous drag force F
D
i
, is quite arbitrarily added to F
i
to
68
