Brennen Ch.E. Fundamentals of Multiphase Flow

Подождите немного. Документ загружается.

gradient. Inspection of the form of the basic equations (for example the con-

tinuity equation, 1.21 or the momentum equation 1.42) readily demonstrates

that additional averaging terms will be introduced because the average of a

product is diﬀerent from the product of averages. In single phase ﬂows, the

Reynolds stress terms in the averaged equations of motion for turbulent ﬂows

are a prime example of this phenomenon. We will use the name quadratic

rectiﬁcation terms to refer to the appearance in the averaged equations of

motion of the mean of two ﬂuctuating components of velocity and/or volume

fraction. Multiphase ﬂows will, of course, also exhibit conventional Reynolds

stress terms when they become turbulent (see section 1.3 for more on the

complicated subject of turbulence in multiphase ﬂows). But even multiphase

ﬂows that are not turbulent in the strictest sense will exhibit variations in

the velocities due the ﬂows around particles and these variations will yield

quadratic rectiﬁcation terms. These must be recognized and modeled when

considering the eﬀects of locally non-uniform and unsteady velocities on the

equations of motion. Much more has to be learned of both the laminar and

turbulent quadratic rectiﬁcation terms before these can be conﬁdently in-

corporated in model equations for multiphase ﬂow. Both experiments and

computer simulation will be valuable in this regard.

One simpler example in which the ﬂuctuations in velocity have been mea-

sured and considered is the case of concentrated granular ﬂows in which di-

rect particle-particle interactions create particle velocity ﬂuctuations. These

particle velocity ﬂuctuations and the energy associated with them (the so-

called granular temperature) have been studied both experimentally and

computationally (see chapter 13) and their role in the eﬀective continuum

equations of motion is better understood than in more complex multiphase

ﬂows.

With two interacting phases or components, the additional terms that

emerge from an averaging process can become extremely complex. In recent

decades a number of valiant eﬀorts have been made to codify these issues

and establish at least the forms of the important terms that result from these

interactions. For example, Wallis (1991) has devoted considerable eﬀort to

identify the inertial coupling of spheres in inviscid, locally irrotational ﬂow.

Arnold, Drew and Lahey (1989) and Drew (1991) have focused on the ap-

plication of cell methods (see section 2.4.3) to interacting multiphase ﬂows.

Both these authors as well as Sangani and Didwania (1993) and Zhang and

Prosperetti (1994) have attempted to include the ﬂuctuating motions of the

particles (as in granular ﬂows) in the construction of equations of motion for

the multiphase ﬂow; Zhang and Prosperetti also provide a useful compar-

ative summary of these various averaging eﬀorts. However, it is also clear

that these studies have some distance to go before they can be incorporated

into any real multiphase ﬂow prediction methodology.

1.4.3 Averaging in pipe ﬂows

One speciﬁc example of a quadratic rectiﬁcation term (in this case a dis-

crepancy between the product of an average and the average of a product)

is that recognized by Zuber and Findlay (1965). In order to account for the

variations in velocity and volume fraction over the cross-section of a pipe

in constructing the one-dimensional equations of pipe ﬂow, they found it

necessary to introduce a distribution parameter, C

, deﬁned by

αj

α j

(1.84)

where the overbar now represents an average over the cross-section of the

pipe. The importance of C

is best demonstrated by observing that it follows

from equations 1.16 that the cross-sectionally averaged volume fraction,

is now related to the volume ﬂuxes,

and j

,by

+ j

)

(1.85)

Values of C

of the order of 1.13 (Zuber and Findlay 1965) or 1.25 (Wallis

1969) appear necessary to match the experimental observations.

1.4.4 Modeling with the combined phase equations

One of the simpler approaches is to begin by modeling the combined phase

equations 1.24, 1.46 and 1.67 and hence avoid having to codify the mass,

force and energy interaction terms. By deﬁning mixture properties such as

the density, ρ, and the total volumetric ﬂux, j

, one can begin to construct

equations of motion in terms of those properties. But none of the summa-

tion terms (equivalent to various weighted averages) in the combined phase

equations can be written accurately in terms of these mixture properties.

For example, the summations,



and



(1.86)

are not necessarily given with any accuracy by ρj

and ρj

. Indeed, the

discrepancies are additional rectiﬁcation terms that would require modeling

in such an approach. Thus any eﬀort to avoid addressing the mass, force and

energy interaction terms by focusing exclusively on the mixture equations

of motion immediately faces diﬃcult modeling questions.

1.4.5 Mass, force and energy interaction terms

Most multiphase ﬂow modeling eﬀorts concentrate on the individual phase

equations of motion and must therefore face the issues associated with con-

struction of I

, the mass interaction term, F

, the force interaction term,

and E

, the energy interaction term. These represent the core of the prob-

lem in modeling multiphase ﬂows and there exist no universally applicable

methodologies that are independent of the topology of the ﬂow, the ﬂow

pattern. Indeed, eﬀorts to ﬁnd systems of model equations that would be

applicable to a range of ﬂow patterns would seem fruitless. Therein lies the

main problem for the user who may not be able to predict the ﬂow pattern

and therefore has little hope of ﬁnding an accurate and reliable method to

predict ﬂow rates, pressure drops, temperatures and other ﬂow properties.

The best that can be achieved with the present state of knowledge is to at-

tempt to construct heuristic models for I

, F

,andE

given a particular

ﬂow pattern. Substantial eﬀorts have been made in this direction partic-

ularly for dispersed ﬂows; the reader is directed to the excellent reviews

by Hinze (1961), Drew (1983), Gidaspow (1994) and Crowe et al. (1998)

among others. Both direct experimentation and computer simulation have

been used to create data from which heuristic expressions for the interaction

terms could be generated. Computer simulations are particularly useful not

only because high ﬁdelity instrumentation for the desired experiments is of-

ten very diﬃcult to develop but also because one can selectively incorporate

a range of diﬀerent eﬀects and thereby evaluate the importance of each.

It is important to recognize that there are several constraints to which

any mathematical model must adhere. Any violation of those constraints is

likely to produce strange and physically inappropriate results (see Garabe-

dian 1964). Thus, the system of equations must have appropriate frame-

indiﬀerence properties (see, for example, Ryskin and Rallison 1980). It must

also have real characteristics; Prosperetti and Jones (1987) show that some

models appearing in the literature do have real characteristics while others

do not.

In this book chapters 2, 3 and 4 review what is known of the behavior of

individual particles, bubbles and drops, with a view to using this information

to construct I

, F

,andE

and therefore the equations of motion for

particular forms of multiphase ﬂow.

SINGLE PARTICLE MOTION

2.1 INTRODUCTION

This chapter will brieﬂy review the issues and problems involved in con-

structing the equations of motion for individual particles, drops or bubbles

moving through a ﬂuid. For convenience we shall use the generic name par-

ticle to refer to the ﬁnite pieces of the disperse phase or component. The

analyses are implicitly conﬁned to those circumstances in which the interac-

tions between neighboring particles are negligible. In very dilute multiphase

ﬂows in which the particles are very small compared with the global dimen-

sions of the ﬂow and are very far apart compared with the particle size, it

is often suﬃcient to solve for the velocity and pressure, u

,t)andp(x

,t),

of the continuous suspending ﬂuid while ignoring the particles or disperse

phase. Given this solution one could then solve an equation of motion for

the particle to determine its trajectory. This chapter will focus on the con-

struction of such a particle or bubble equation of motion.

The body of ﬂuid mechanical literature on the subject of ﬂows around

particles or bodies is very large indeed. Here we present a summary that

focuses on a spherical particle of radius, R, and employs the following com-

mon notation. The components of the translational velocity of the center

of the particle will be denoted by V

(t). The velocity that the ﬂuid would

have had at the location of the particle center in the absence of the particle

will be denoted by U

(t). Note that such a concept is diﬃcult to extend to

the case of interactive multiphase ﬂows. Finally, the velocity of the particle

relative to the ﬂuid is denoted by W

(t)=V

− U

Frequently the approach used to construct equations for V

(t)(orW

(t))

given U

,t) is to individually estimate all the ﬂuid forces acting on the

particle and to equate the total ﬂuid force, F

,tom

/dt (where m

the particle mass, assumed constant). These ﬂuid forces may include forces

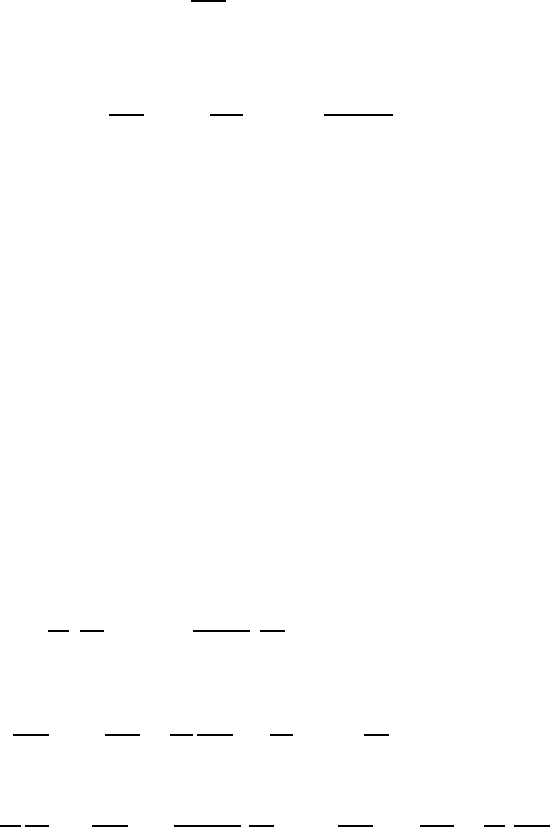
due to buoyancy, added mass, drag, etc. In the absence of ﬂuid acceleration

(dU

/dt = 0) such an approach can be made unambiguously; however, in

the presence of ﬂuid acceleration, this kind of heuristic approach can be

misleading. Hence we concentrate in the next few sections on a fundamental

ﬂuid mechanical approach, that minimizes possible ambiguities. The classical

results for a spherical particle or bubble are reviewed ﬁrst. The analysis is

conﬁned to a suspending ﬂuid that is incompressible and Newtonian so that

the basic equations to be solved are the continuity equation

∂u

∂x

=0 (2.1)

and the Navier-Stokes equations



∂u

∂x



= −

∂p

∂x

− ρ

∂

∂x

(2.2)

where ρ

and ν

are the density and kinematic viscosity of the suspending

ﬂuid. It is assumed that the only external force is that due to gravity, g.

Then the actual pressure is p



= p − ρ

gz where z is a coordinate measured

vertically upward.

Furthermore, in order to maintain clarity we conﬁne our attention to

rectilinear relative motion in a direction conveniently chosen to be the x

direction.

2.2 FLOWS AROUND A SPHERE

2.2.1 At high Reynolds number

For steady ﬂows about a sphere in which dU

/dt = dV

/dt = dW

/dt =0,it

is convenient to use a coordinate system, x

, ﬁxed in the particle as well as

polar coordinates (r, θ) and velocities u

as deﬁned in ﬁgure 2.1.

Then equations 2.1 and 2.2 become

∂

∂r

r sin θ

∂

∂θ

sin θ) = 0 (2.3)

and



∂u

∂t

+ u

∂u

∂r

∂u

∂θ

−



= −

∂p

∂r

(2.4)

+ρ



∂

∂r



∂u

∂r



sin θ

∂

∂θ



sin θ

∂u

∂θ



−

∂u

∂θ



Figure 2.1. Notation for a spherical particle.



∂u

∂t

+ u

∂u

∂r

∂u

∂θ



= −

∂p

∂θ

(2.5)

+ρ



∂

∂r



∂u

∂r



sin θ

∂

∂θ



sin θ

∂u

∂θ



∂u

∂θ

−

sin



The Stokes streamfunction, ψ, is deﬁned to satisfy continuity automatically:

sin θ

∂ψ

∂θ

; u

= −

r sin θ

∂ψ

∂r

(2.6)

and the inviscid potential ﬂow solution is

ψ = −

sin

θ −

sin

θ (2.7)

= −W cos θ −

cos θ (2.8)

=+W sin θ −

sin θ (2.9)

φ = −Wrcos θ +

cos θ (2.10)

where, because of the boundary condition (u

)

r=R

= 0, it follows that D =

−WR

/2. In potential ﬂow one may also deﬁne a velocity potential, φ,such

that u

= ∂φ/∂x

. The classic problem with such solutions is the fact that

the drag is zero, a circumstance termed D’Alembert’s paradox. The ﬂow is

symmetric about the x

plane through the origin and there is no wake.

The real viscous ﬂows around a sphere at large Reynolds numbers,

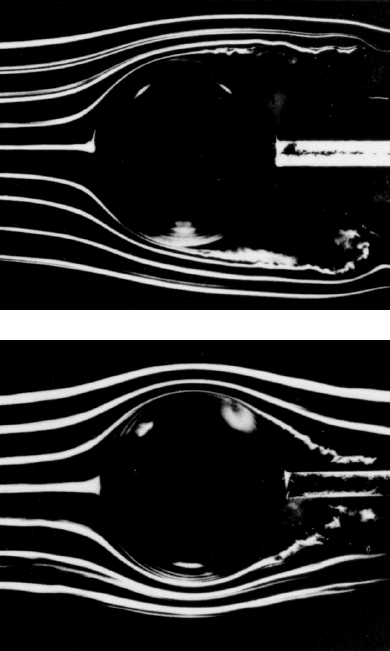
Figure 2.2. Smoke visualization of the nominally steady ﬂows (from

left to right) past a sphere showing, at the top, laminar separation at

Re =2.8 × 10

and, on the bottom, turbulent separation at Re =3.9 × 10

Photographs by F.N.M.Brown, reproduced with the permission of the Uni-

versity of Notre Dame.

Re =2WR/ν

> 1, are well documented. In the range from about 10

3 × 10

, laminar boundary layer separation occurs at θ

∼

◦

and a large

wake is formed behind the sphere (see ﬁgure 2.2). Close to the sphere the

near-wake is laminar; further downstream transition and turbulence occur-

ring in the shear layers spreads to generate a turbulent far-wake. As the

Reynolds number increases the shear layer transition moves forward until,

quite abruptly, the turbulent shear layer reattaches to the body, resulting

in a major change in the ﬁnal position of separation (θ

∼

120

◦

)andinthe

form of the turbulent wake (ﬁgure 2.2). Associated with this change in ﬂow

Figure 2.3. Drag coeﬃcient on a sphere as a function of Reynolds number.

Dashed curves indicate the drag crisis regime in which the drag is very

sensitive to other factors such as the free stream turbulence.

pattern is a dramatic decrease in the drag coeﬃcient, C

(deﬁned as the

drag force on the body in the negative x

direction divided by

πR

from a value of about 0.5 in the laminar separation regime to a value of

about 0.2 in the turbulent separation regime (ﬁgure 2.3). At values of Re

less than about 10

the ﬂow becomes quite unsteady with periodic shedding

of vortices from the sphere.

2.2.2 At low Reynolds number

At the other end of the Reynolds number spectrum is the classic Stokes

solution for ﬂow around a sphere. In this limit the terms on the left-hand side

of equation 2.2 are neglected and the viscous term retained. This solution

has the form

ψ =sin



−

+ Br



(2.11)

=cosθ



−W +



(2.12)

= − sin θ



−W −



(2.13)

where A and B are constants to be determined from the boundary conditions

on the surface of the sphere. The force, F ,ontheparticle in the x

direction

πR



−



(2.14)

Several subcases of this solution are of interest in the present context. The

ﬁrst is the classic Stokes (1851) solution for a solid sphere in which the no-slip

boundary condition, (u

)

r=R

= 0, is applied (in addition to the kinematic

condition (u

)

r=R

= 0). This set of boundary conditions, referred to as the

Stokes boundary conditions, leads to

A = −

,B=+

3WR

and F

= −6πρ

WR (2.15)

The second case originates with Hadamard (1911) and Rybczynski (1911)

who suggested that, in the case of a bubble, a condition of zero shear stress

on the sphere surface would be more appropriate than a condition of zero

tangential velocity, u

. Then it transpires that

A =0 ,B=+

and F

= −4πρ

WR (2.16)

Real bubbles may conform to either the Stokes or Hadamard-Rybczynski

solutions depending on the degree of contamination of the bubble surface,

as we shall discuss in more detail in section 3.3. Finally, it is of interest to

observe that the potential ﬂow solution given in equations 2.7 to 2.10 is also

asubcasewith

A =+

,B=0 and F

= 0 (2.17)

However, another paradox, known as the Whitehead paradox, arises when

the validity of these Stokes ﬂow solutions at small (rather than zero)

Reynolds numbers is considered. The nature of this paradox can be demon-

strated by examining the magnitude of the neglected term, u

∂u

/∂x

,in

the Navier-Stokes equations relative to the magnitude of the retained term

∂

/∂x

∂x

. As is evident from equation 2.11, far from the sphere the

former is proportional to W

R/r

whereas the latter behaves like ν

WR/r

It follows that although the retained term will dominate close to the body

(provided the Reynolds number Re =2WR/ν

 1), there will always be a

radial position, r

,givenbyR/r

= Re beyond which the neglected term will

exceed the retained viscous term. Hence, even if Re  1, the Stokes solution

is not uniformly valid. Recognizing this limitation, Oseen (1910) attempted

to correct the Stokes solution by retaining in the basic equation an approxi-

mation to u

∂u

/∂x

that would be valid in the far ﬁeld, −W∂u

/∂x

.Thus

the Navier-Stokes equations are approximated by

−W

∂u

∂x

= −

∂p

∂x

+ ν

∂

∂x

(2.18)

Oseen was able to ﬁnd a closed form solution to this equation that satisﬁes

the Stokes boundary conditions approximately:

ψ = −WR



sin

R sin

3ν

(1 + cos θ)

2WR



1 − e

2ν

(1−cos θ)



(2.19)

which yields a drag force

= −6πρ





(2.20)

It is readily shown that equation 2.19 reduces to equation 2.11 as Re → 0.

The corresponding solution for the Hadamard-Rybczynski boundary con-

ditions is not known to the author; its validity would be more question-

able since, unlike the case of Stokes boundary conditions, the inertial terms

∂u

/∂x

are not identically zero on the surface of the bubble.

Proudman and Pearson (1957) and Kaplun and Lagerstrom (1957) showed

that Oseen’s solution is, in fact, the ﬁrst term obtained when the method

of matched asymptotic expansions is used in an attempt to patch together

consistent asymptotic solutions of the full Navier-Stokes equations for both

the near ﬁeld close to the sphere and the far ﬁeld. They also obtained the

next term in the expression for the drag force.

= −6πρ



Re +

160





+0(Re

)



(2.21)

The additional term leads to an error of 1% at Re =0.3 and does not,

therefore, have much practical consequence.

The most notable feature of the Oseen solution is that the geometry of

the streamlines depends on the Reynolds number. The downstream ﬂow is

not a mirror image of the upstream ﬂow as in the Stokes or potential ﬂow

solutions. Indeed, closer examination of the Oseen solution reveals that,

downstream of the sphere, the streamlines are further apart and the ﬂow

is slower than in the equivalent upstream location. Furthermore, this eﬀect

increases with Reynolds number. These features of the Oseen solution are

entirely consistent with experimental observations and represent the initial

development of a wake behind the body.

The ﬂow past a sphere at Reynolds numbers between about 0.5andseveral

thousand has proven intractable to analytical methods though numerical so-