Braun J., van der Beek P., Batt G. Quantitative Thermochronology: Numerical Methods for the Interpretation of Thermochronological Data

Подождите немного. Документ загружается.

188 The evolution of passive-margin escarpments

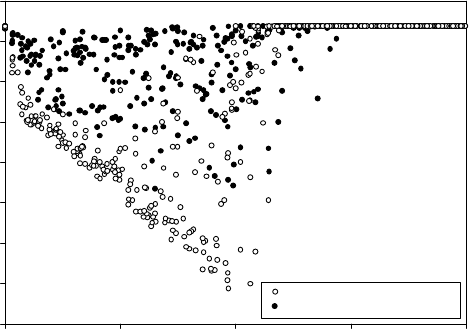
Note the different patterns of age distribution predicted by the respective models

(Figure 12.8): the escarpment-retreat model gives ages clearly decreasing from

the coastline to the escarpment, because the peak of denudation migrates inland

with the escarpment (e.g., Figure 12.6), whereas the plateau-degradation model

predicts less variation in the ages on the coastal strip, which are all close to the

age of break-up.

Braun and van der Beek (2004) performed a sensitivity analysis on the bound-

ary conditions, the initial conditions and the parameters of the landscape-evolution

model (the initial elevation of the escarpment, retreat rate, equivalent elastic

thickness and width of the escarpment zone) in order to test under what cir-

cumstances apatite (U–Th)/He and fission-track data can reliably be used to

infer the evolution of the margin. To do this, they systematically searched the

parameter space, using simplified kinematic models of escarpment development

that simulate the behaviour observed in the Cascade models. Conditions that

are favourable are those necessary to produce sufficient exhumation to reset the

thermochronological system. They include a tall escarpment, a high geothermal

gradient and/or a low flexural rigidity of the lithosphere. Braun and van der

Beek (2004) demonstrated that, to determine the rate and mode of escarpment

migration from low-temperature thermochronology, one needs to collect samples

Distance from coast (km)

0 20406080

(U–Th)/He age (Myr)

100

120

140

160

Plateau-Degradation Scenario

Escarpment-Retreat Scenario

Fig. 12.8. Comparison of the (U–Th)/He ages predicted by the models in Fig-

ure 12.7, as a function of distance from the coastline. After Braun and van der

Beek (2004). Reproduced with permission from the American Geophysical

Union.

12.5 Combining thermochronometers and modelling 189

along transects perpendicular as well as parallel to the escarpment. The tight-

est constraints on escarpment development are provided by (in ascending order)

the minimum thermochronological age encountered seaward of the escarpment,

the location of where the minimum age is found, the slope of the age–distance

relationship (in a direction perpendicular to the coast) and the slope of the age–

elevation relationship (from a transect parallel to the escarpment).

To address the issue of whether limited and error-prone real-world data con-

strain evolutionary scenarios, Braun and van der Beek (2004) used the Neighbour-

hood Algorithm (see Section 8.5) to search the parameter space for best fits to an

existing dataset. They used the Bega Valley region of the SE Australian escarp-

ment as a test case, since this is the only area for which both apatite fission-track

(e.g., Gleadow et al., 2002; Persano, 2003) and (U–Th)/He (Persano et al., 2002;

Persano, 2003) data are currently available. The eastern Australian margin devel-

oped as a result of oblique rifting in the Tasman Sea from ∼95Myr ago onwards,

with oceanic spreading taking place in the Tasman Sea ∼80 Myr ago (Gaina

et al., 1998). The margin is characterised by an approximately 1-km-high escarp-

ment running along its entire length of ∼2500 km and separating a low-elevation

coastal strip from a high-elevation but low-relief upland region. In southernmost

New South Wales, where the data were collected (Figure 12.9), the escarpment is

cut into Paleozoic granites and metamorphic rocks and is located ∼35 km from

the coast. In this area, the escarpment forms a secondary drainage divide between

linear river systems that flow to the Tasman Sea through relatively deeply incised

Longitude

149.0 149.5 150.0

Latitude

–36.6

–36.5

–36.4

–36.3

200

400

600

800

1000

1200

Canberra

Sydney

Melbourne

Fig. 12.9. The topography of the study area along the coast of southeastern

Australia (rectangle in inset) showing the location of (U–Th)/He samples from

Persano et al. (2002). After Braun and van der Beek (2004). Reproduced with

permission from the American Geophysical Union.

190 The evolution of passive-margin escarpments

(a) Plateau-Downwearing Scenario

(b) Escarpment-Retreat Scenario

(°Ckm

–1

)

(°Ckm

–1

)

10 15

(km)

Fig. 12.10. Locations of model runs as a function of the elastic thickness T

and

surface heat flow G

during a Neighbourhood Algorithm search. As the routine

searches the parameter space for best-fit models, the highest density of models

(indicated by the grey discs) corresponds to the locations of local minima in

misfit. After Braun and van der Beek (2004). Reproduced with permission from

the American Geophysical Union.

12.5 Combining thermochronometers and modelling 191

valleys and the Snowy River and its tributaries on the highland plateau, which

flow southwards into the Bass Strait (van der Beek and Braun, 1999).

Whereas (U–Th)/He data are close to the age of break-up (100 Myr) sea-

wards of the escarpment and significantly older inland, apatite fission-track data

are older than the age of break-up throughout the area, although they are also

young towards the coastline. The inversion results (Figure 12.10) show that the

(U–Th)/He data, even though limited, are consistent with low flexural rigidity

and/or a high geothermal gradient during and after break-up. They also require

escarpment development to have occurred during the first 15 Myr after the onset

of rifting, either through downwasting (plateau degradation) or by very rapid

retreat, followed by stabilisation at the present-day escarpment location. In this

setting, the apatite fission-track data, in contrast, cannot provide this constraint,

since rocks have been exhumed from the partial-annealing zone only. This exam-

ple shows the importance of combining different thermochronological datasets to

study rifted-margin evolution and to constrain the numerical models.

Thermochronology in active tectonic settings

The coupling between erosion and tectonics is most likely to be efficient

in regions of ongoing tectonic activity, especially in regions of conti-

nental convergence where the collision between two continents leads to

crustal thickening and, by isostasy, to surface uplift. This uplift causes

relief (i.e. slope) to be created, which triggers erosion by channel inci-

sion or, under colder climatic conditions, the formation of glaciers that

will rapidly reshape the landform.

In this chapter, we are going to investigate the effect of continental

collision on the temperature structure of the crust; we will also present

some of the most widely accepted models for crustal deformation and,

most importantly, describe the respective consequences they have for

the path followed by rock particles as they travel through the orogen,

ultimately to be exposed at the surface. The combination of these pro-

cesses will provide us with appropriate (that is, quantitative) constraints

on the predicted temperature history of particles from which we should

be able to predict cooling ages.

At the end of this chapter we will demonstrate how these predictions

can then be used to constrain the tectonic evolution of an active mountain

belt, including the timing of the onset of convergence, the present-day

rate of convergence and its variation along the strike of the orogen. To

illustrate this approach, we will consider a dataset collected in the South-

ern Alps of New Zealand that has been interpreted using state-of-the-art

quantitative methods (Batt and Braun, 1999; Herman et al., 2006).

13.1 A simple model for continental collision

In many cases, continental collision can be regarded as the end product of the

closure of an oceanic basin bounded on at least one of its sides by a subduction

zone (Willett et al., 1993). Sediment that lies on top of the oceanic crust is

progressively scraped off by the overlying continent and accumulates in the

192

13.1 A simple model for continental collision 193

Accretionary Wedge

Forearc Basin

Lithosphere

Oceanic

Continental

Mantle

Continental Crust

Continental Mantle

Oceanic

Lithosphere

Foreland Basin

Passive-Margin

Sequence

Continental Crust

= V

;

=0; V

(a) Active Margin

(b) Continent–continent Collision

Volcanic Arc

Basement

Fig. 13.1. (a) An accretionary prism in a subduction setting. (b) A conceptual

model for the collision between two continents in which the mantle part of the

lithosphere undergoes subduction while the lighter overlying crust is forced to

thicken. (c) The modelling analogue for these two scenarios. Modified from

Willett et al. (1993). Reproduced with permission from the Geological Society

of America.

subduction trough, forming an accretionary prism (Figure 13.1(a)). The internal

dynamics of the wedge is adequately represented as that of a critical wedge of

frictional material at or near failure (Dahlen et al., 1984).

The concept of a critical wedge can be extended to describe the behaviour of

the continental crust at a convergent plate boundary in the absence of oceanic

lithosphere. Because of their lower density, continental rocks are unlikely to be

subducted into the underlying denser mantle. Rather, it can be considered that

194 Thermochronology in active tectonic settings

(a) Basic Behaviour

ErosionErosion

‘Pro’-Side ‘Retro’-Side

Pro-Shear

Retro-Shear

(b) Exhumation

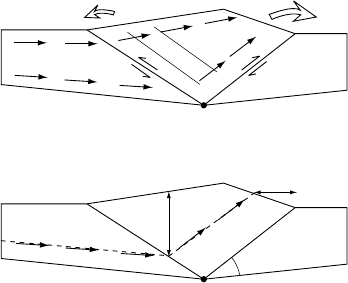
Fig. 13.2. (a) The velocity structure within an actively deforming doubly-vergent

orogenic wedge where tectonic influx is in equilibrium with erosional outflux.

(b) The path of a rock particle.

they will be decoupled from the underlying continental lithospheric mantle and

deformed, as shown in Figure 13.1(b).

During a continental collision of this sort, the crust can be regarded as being

forced to shorten by the presence of a velocity discontinuity along its base that

represents the subduction process in the mantle (Figure 13.1(c)). The shortening

causes the formation of two oppositely dipping shear zones that root in the velocity

discontinuity (Willett et al., 1993) (Figure 13.2(a)). The exact geometry of the

shear zones is a function of the rheology of the crust; i.e. whether it is mostly

brittle or ductile (Willett, 1999b) or whether it is characterised by strain softening

(Beaumont et al., 1996). This dynamic model for the evolution of an orogenic belt

has been termed the doubly-vergent critical-wedge model (Koons, 1990, 1994;

Willett et al., 1993).

Following finite convergence, the system rapidly becomes asymmetrical, with

one of the two shear zones, the one that developed on the side of the collision to

which the velocity discontinuity is attached, accumulating finite strain, with the

other only transiently active and accumulating small strain (Willett et al., 1993).

The static side of the orogen, i.e. the one to which the discontinuity is attached,

is called the retro-side of the orogen; the other, the pro-side (Willett et al.,

1993) (Figure 13.2(a)). As deformation proceeds, surface topography is generated,

which, for a given set of climatic conditions, can be more or less efficiently eroded

away. This results in the net movement of rock particles towards the surface. If

the conditions are such that erosion is efficient, a steady-state situation can be

13.1 A simple model for continental collision 195

(a) Uniform Erosion/Precipitation

Elevation

Precipitation

Exhumation

ErosionErosion

(b) Orographic Precipitation Focussed on Retro-Side

Erosion

Elevation

Precipitation

Exhumation

Dominant

Wind

Direction

Erosion

Dominant

Wind

Direction

Elevation

Precipitation

Exhumation

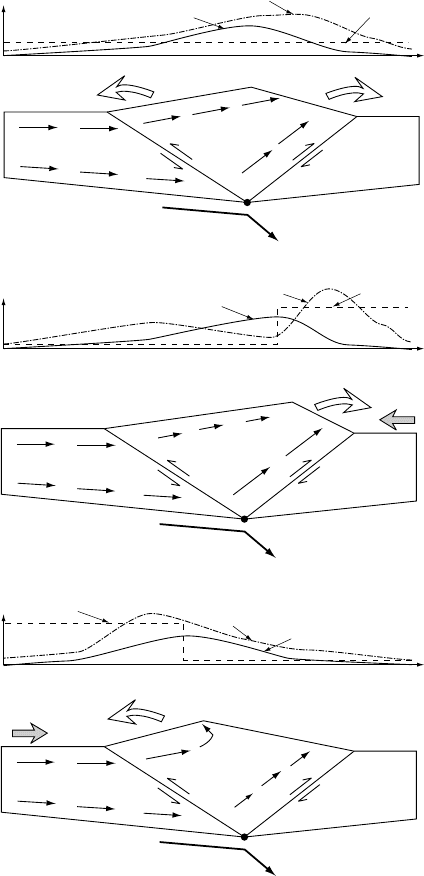
Fig. 13.3. Rock paths in an orogen where erosion is (a) uniform, (b) concentrated

on the retro-side of the orogen and (c) concentrated on the pro-side of the orogen.

196 Thermochronology in active tectonic settings

achieved, in which the collisional flux of rock mass into the orogen is equal to

the erosional flux out of the orogen. In this situation the path of rock particles

through the orogen is relatively simple, as shown in Figure 13.2.

Rocks enter the orogen at a given depth and first experience a relatively slow

increase in pressure and relatively uniform thickening corresponding to their

entry into the broad orogenic wedge (Little, 2004); they traverse the pro-shear,

where they experience a short but intense pulse of reverse shearing; they then

enter the core of the orogen from which they are progressively exhumed by

thrusting along the retro-shear. The important point to notice here is that the

depth reached by rocks as they ‘travel’ through the orogen is maximum for those

rocks that will be exhumed closest to the surface expression of the retro-shear

(Figure 13.2(b)).

The dynamics of this system and, consequently, the geometry of the rock-

particle paths are strongly dependent on the nature and efficiency of the erosional

processes at the surface of the orogen (Willett et al., 1993; Willett, 1999a),

as illustrated in Figure 13.3. For example, if the topography created by the

crustal thickening causes a perturbation in the local climatic conditions such that

orographic effects enhance the level of precipitation on one of the two sides of

the orogen, one can expect greater erosion and thus a higher exhumation rate on

the ‘wet’ side of the mountain belt. This, in turn, can cause the internal force

balance within the orogen to shift and lead to important changes in its dynamics

and thus in the paths followed by rock particles, as shown in Figure 13.3.

This feedback mechanism has been demonstrated in numerous studies based

on numerical models of the coupled tectonics–erosion system (Willett et al.,

1993, 2001; Beaumont et al., 1996; Batt and Braun, 1997; Willett, 1999a) and is

now widely called upon to explain variations in the surface geology of diverse

small mountain belts such as the Southern Alps of New Zealand, Taiwan and the

Olympic Mountains.

13.2 Heat advection in mountain belts

Where exhumation of rocks towards the surface advects heat more rapidly than

it can be dispersed by conductive heat transport, there is a net transfer of heat to

the upper crust, perturbing the thermal structure of the affected region. A one-

dimensional consideration of this phenomenon discussed in Chapter 5 showed

that efficient heat transport occurs in this way when the rate of exhumation,

and the thickness of the layer being exhumed, L, are such that the dimensionless

Péclet number Pe =

EL/ is greater than 1.

Quantification of this process for more complex velocity distributions is not

trivial and cannot realistically be achieved using simple analytical solutions such

13.2 Heat advection in mountain belts 197

as those developed in Section 5.1. A more pragmatic and flexible approach capable

of incorporating the effects of arbitrary material paths and spatial variability in

material properties is required, which invariably involves the numerical solution

of the heat-transfer equation, as explained in Section 5.3 and Chapter 7. In this

section we will simply describe the results obtained in a growing number of studies

(Koons, 1987; Shi et al., 1996; Jamieson et al., 1996; Batt and Braun, 1997, 1999)

in which the temperature histories of rock particles as they travel through an

active mountain belt have been simulated by solving the heat-transport equation

numerically, typically in two dimensions and using a velocity field similar to the

one shown in Figure 13.2. Such a velocity field can be either prescribed or derived

from the numerical solution of the force-balance equation under conditions of

continental convergence and surface erosion. Here we will focus on the results of

these numerical solutions, not the details of how they were obtained. For details

on how one can define a kinematic representation of a tectonic velocity field or

calculate it from a dynamic model (by solution of the force-balance equation),

the reader is referred to Batt and Braun (1997), Braun and Sambridge (1994) or

Herman et al. (2006), among many others.

Advection of heat by the velocity field described in Figure 13.2 leads to an

upward deflection of the isotherms in the central region of the orogen, i.e. in

the region of maximum exhumation between the two conjugate shear zones (Fig-

ure 13.4(b)). The temperature perturbation is partly transferred laterally to the

adjacent regions, causing a noticeable heating of the regions on either side of the

exhuming orogenic plug and a corresponding reduction of the temperature within

the orogenic plug itself. A rock particle passing through the perturbed temperature

field first experiences a moderate increase in temperature as it enters the orogen;

this increase in temperature is accompanied by an increase in pressure that cor-

responds to the entry of the particle into the region of thickened crust. Once the

particle has made its way through the pro-shear, it experiences rapid decompres-

sion during its exhumation; during the early stages of its ascent, however, the

particle experiences little cooling because it traverses a nearly isothermal region

at the core of the orogen. It is only when it approaches the cold free surface of

the orogen that it begins to experience substantial cooling.

This complex history can be illustrated if one plots the trajectory of the particle

in pressure–temperature space, as done in Figure 13.4(a) for four particles that

will end up at different locations along the surface of the orogen. All particles

follow a counter-clockwise P–T trajectory that is made of three main sections:

firstly a period of modest increases in temperature and pressure, followed by a

period of isothermal decompression and, finally, an episode of rapid cooling with

slowly decreasing pressure. The maximum temperature and pressure vary among

the particles and increase on going from the pro- to the retro-side of the orogen.