Braibant S., Giacomelli G., Spurio M. Particles and Fundamental Interactions: An Introduction to Particle Physics
Подождите немного. Документ загружается.

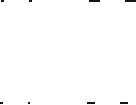
7.3 The Strong Interaction Cross-Section 139
the two reactions pp ! d
C
and pn ! d
0
. The isospin composition of the
initial and final states is
I
p C p
„
ƒ‚…
1
!
d C
C
01
„
ƒ‚ …
1
(7.5)
I
p C n
„
ƒ‚…
0;1
!
d C
0
01
„
ƒ‚…
1
: (7.6)
The initial states are a pure state of isospin 1 for (7.5) and a mixed state, 50% of
isospin 0 and 50% of isospin 1, for (7.6). Both reactions have final states with total
isospin equal to one and occur via strong interaction, which conserves isospin. The
first reaction is allowed, while the second is allowed only for the 50% of the cases
with initial isospin I D 1. It follows that .pp ! d
C
/=.pn ! d
0
/ D 2,as
experimentally observed.
Isospin for quarks. As anticipated, p and n are not fundamental objects, and
are made of .u;d/ quarks. The symmetry in terms of isospin should be reflected
in symmetry in terms of quarks. The .u;d/ quarks can be regarded as members
of a strong isospin doublet (I D 1=2, with I
z
.u/ DC1=2, I
z
.d / D1=2)
similarly to the neutron and proton. As we shall see in Sect. 7.14.5, the masses of
the u and d quarks are almost equal and very small in comparison to the nucleon
mass. The mass of hadrons made of the lighter .u;d/ quarks receive a dominant
contribution from the energy of the strong interaction field to which quarks are
subjected. This interaction mechanism is described by Quantum Chromodynamics
(QCD), Sect. 11.9. The isospin independence of strong interaction reflects the fact
that color forces are independent of the quark flavor.Thes; c; b; t quarks are
strong isospin singlets, with I D 0; their mass is significantly larger than that of
u;d quarks and the mass of hadrons made of heavier quarks is highly dependent on
the quark flavor.
7.3 The Strong Interaction Cross-Section
As discussed in Chap.4, one way to obtain information on the interaction potential
comes from the measurement of the cross-section. In the case of a short-range
potential, that is negligible for r>R
0
(in the case of the Yukawa potential
R
0
a), we expect a purely geometric cross-section. The geometric cross-section
corresponds to the effective area of the target, namely,
D R
2
0
: (7.7)
This is valid when the size of the projectile is negligible compared to that of the
target. The projectile particle wave length is given by the de Broglie length (3.1)

140 7 Hadron Interactions at Low Energies and the Static Quark Model
¯ D„=p D 1:24 fm=2p (GeV/c). Only projectiles with momentum p 1GeV/c
can be considered as point-like with respect to targets with nuclear dimensions
(1fm).
The elastic collisions occur when the projectile and the target remain unchanged
before and after the collision, and have the same energy in the center of mass
(c.m.) system. At high energy, the inelastic collisions are dominant; it is therefore
possible that the incident particle (or the target) be excited, and that new particles are
produced. These new possibilities are accounted for by the inelastic cross-section,
inel
. The total cross-section is the sum of the elastic and inelastic ones, namely,
tot
D
el
C
inel
.
The hypothesis that the nuclear forces are short-range can be qualitatively
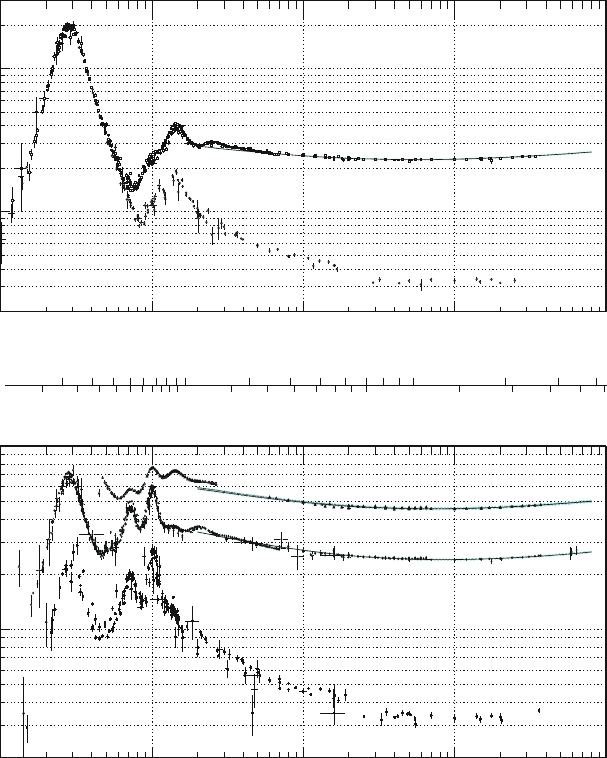
checked by observing Figs. 7.1 and 7.2. The former shows the measurements of
pion-proton cross-sections and the latter the measurements of proton–proton (and
pp) cross-sections as a function of the momentum p
lab
of the incoming projectile
particle. For p
lab
1 GeV/c, the cross-sections vary only slowly with energy, with
a mean value of
pp
' 40 mb and
p
' 25 mb over a wide momentum range.
The quantity R
0
' 1.1 fm and 0.9 fm can be derived from Eq. 7.7 for the two cases.
They correspond respectively to the p p and p interaction ranges.
In the following, we shall see how this assumption is valid only in a first
approximation. We shall also need to change the description at low energy, where
the condition of negligible size of the projectile is no longer satisfied.
7.3.1 Mean Free Path
The mean free path is a useful quantity for the study of long-lived particles
(Table 7.3) propagating in a given medium. Consider a beam of nuclei or long-
lived hadrons with intensity I (cm
2
s
1
) colliding on a target containing N
n
(nuclei
cm
3
). A target layer dx contains N
n
dx (nuclei cm
2
). Due to the collisions with
the target nuclei, the incident beam is attenuated by the quantity
dI D IN
n
dx (7.8)
where is a proportionality factor with the dimensions of an area. One can interpret
this parameter as an estimate of the geometric size of the target nucleus. By
integrating Eq. 7.8 over a finite thickness x, one obtains
I.x/ D I.0/ e
N
n
x
D I.0/ e
x
D I.0/ e
x=
(7.9)
where I.0/ is the intensity of the incident beam before the target; the quantity D
N
n
is the absorption coefficient, while its inverse,
D 1= D 1=N
n
.cm/; (7.10)
is the mean free path or the collision length. Sometimes, the mean free path is
multiplied by the density of the medium, and is expressed as
7.3 The Strong Interaction Cross-Section 141
10
2
10
–1
110
π
–
p
otal
π
±
d
total
π
–
p
elastic
P
lab
GeV/c
10
10
2
Cross section (mb)
⇓
⇓
√s GeV
πd
πp
1.2 2 3 4 5 6 7 8 9 10 20 30 40
2.2 3 4 5 6 7 8 9 10 20 30 40 50 60
10
10
2
10
2
10
–1
1 10
π
+
p
total
π
+
p
elastic
⇓
P
lab
GeV / c
Cross section (mb)
Fig. 7.1 Measurements of the total and elastic cross-sections for
C
p (upper plot),
p,
˙
d
(bottom plot) collisions [P08]
D = D =N
n
.gcm
2
/: (7.11)
In this case, it corresponds to a path (in cm) in a medium with the density of the
water. Equations 7.10 and 7.11 differ only in the units, and both are used to define the
mean free path. The ratio I.x/=I.0/ D e
N
n
x
is called attenuation. The integration
of Eq. 7.8 is possible only if there is no “shadowing effect” of the target nuclei. This
is true in practice because the nuclear size is small (few fm, see Problem 7.10)
compared to the distance between nuclei.
142 7 Hadron Interactions at Low Energies and the Static Quark Model
√s GeV
1.9 2 10
10
3
10
4
10
2
elastic
total
⇓
pp
10
10
2
Cross section (mb)
P
lab
GeV/c
10
–1
10
3
10
4
10
5
10
6
10
7
10
8
10
2
10
1
elastic
total
⇓
p
_
p
10
10
2
Cross section (mb)
P
lab
GeV/c
10
–1
10
3
10
4
10
5
10
6
10
7
10
8
10
2
10
1
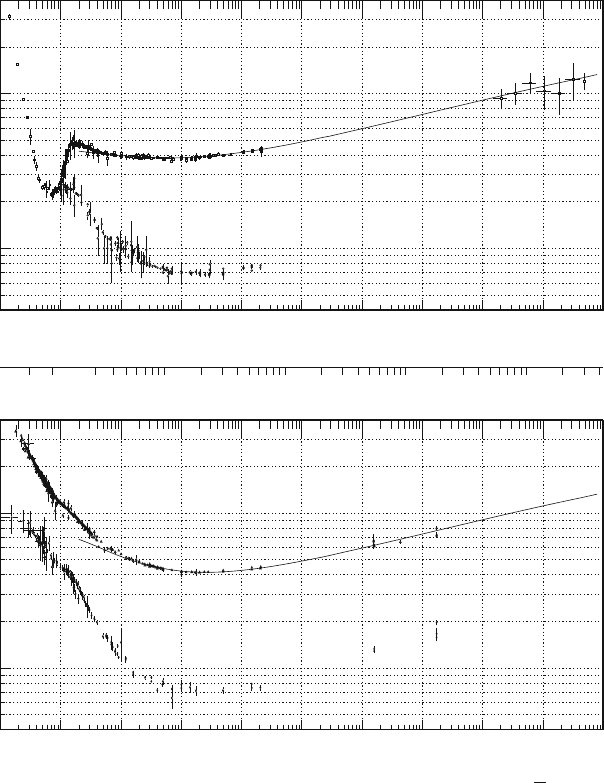
Fig. 7.2 Measurements of the total and elastic cross-sections for pp (upper plot)andpp (lower
plot) collisions [P08]
7.4 Low Energy Hadron-Hadron Collisions
The study of pion-nucleon collisions at low energy (up to a few GeV) has been
historically important in establishing the existence of hadronic resonances and for
the measurements of their masses and quantum numbers.
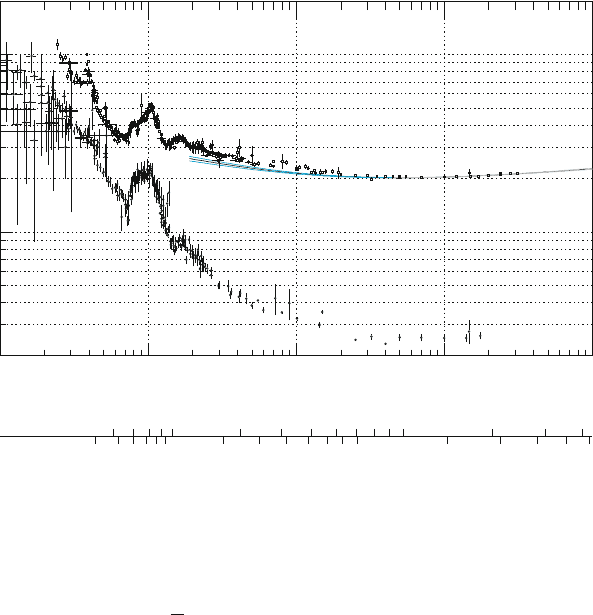
A qualitative idea of the features of hadron-hadron collisions [7G76] can be
obtained by analyzing the measurements of the total and elastic cross-sections
of charged hadrons on hydrogen and deuterium, shown in Figs. 7.1–7.3.For
7.4 Low Energy Hadron-Hadron Collisions 143
Center of mass energy (GeV)
K
±
d
K
±
N
1.6 2 3 4 5 6 7 8 9 10 20 30 40
2.5 3 4 5 6 7 8 9 10 20 30 40 50 60
K
–
p
total
K
–
p
elastic
Cross section (mb)
10
2
10
2
10
3
10
–1
110
10
Fig. 7.3 Measurements of the total and elastic cross-sections for K
p collisions [P08]
c.m. energies smaller than 3 GeV, the total
˙
p; K
p; K
n cross-sections are
characterized by peaks and structures, whose heights decrease with increasing
energy. The K
C
p; pp and pp cross-sections do not have large peaks, and only
present minor structures.
The quantum mechanical formalism used for the study of cross-sections at low
energies is developed in terms of amplitudes and phases of matter waves, in analogy
with the description of optical waves. A fairly detailed description of the formalism
can be found in [P87]. The mathematical function that describes the increases of the
cross-section is derived in Sect. 7.5.
7.4.1 Antibaryons
Baryons, as protons, neutrons and hyperons, are semi-integer spin particles.
According to the Dirac theory, the corresponding charge conjugated states must
exist. These states correspond to antibaryons with opposite fermionic number,
electric charge, magnetic moment and strangeness. The theory is confirmed by
the existence of antileptons, such as the positron .e
C
/,the
C
lepton and the
antineutrinos. To test the Dirac prediction in the hadron system, O. Chamberlain and
E. Segr
`
e (with Wiegand and Ypsilantis) managed, in 1955, to produce antiprotons
with the Bevatron accelerator at the Lawrence Radiation Laboratory in Berkeley.
For this discovery, Segr
`
e and Chamberlain earned the Nobel Prize in 1959.

144 7 Hadron Interactions at Low Energies and the Static Quark Model
Fig. 7.4 Interaction of a K
meson of 4.2 GeV/c momentum, in a bubble chamber filled with
liquid hydrogen. Two charged pions and a
0
are produced in the interaction. The
0
decays
shortly afterwards into a proton and a negative pion (From R.T. Van de Walle, Photo CERN,
Geneva)
An antiproton (p) can be produced in interactions of protons on nuclei through
the reactions pp !
pppp or pn ! pppn that conserve the baryon number and the
electric charge. The reactions only occur if the beam kinetic energy is larger than
6m
p
D 5:6 GeV (Sect. 3.1). The p production is indicated by the presence in the
final state of a particle with the same mass as that of the proton but with an opposite
electric charge. At this energy, many
mesons are produced with a much higher
probability. Particles with mass D m
p
must then be selected by measuring both the
momentum and the speed of the produced particles. The experiment was done using
bending magnets to select negative charged particles and both time-of-flight and
Cherenkov detectors to measure the speed.
Once the method to produce a secondary beam of antiprotons was known, it
was used to produce other antibaryons in p
p annihilations through the reactions
p
p ! baryon C antibaryon. In 1957, Cork, Lamberston and Piccioni discovered
the antineutron (
n) in this way. Shortly after, the
0
was observed in the p
annihilation with liquid hydrogen nuclei in a bubble chamber,
pp !
0
0
.
Other antibaryons were then discovered in the same way: for every baryon, the
corresponding antibaryon was observed. The antibaryons have negative baryon
number, and decay in the charged conjugated states of the corresponding baryons.
For instance, the antineutron decays as
n ! pe
C
e
.
7.4.2 Hadron Resonances
Figure 7.4 shows an event recorded in a hydrogen bubble chamber. An incident K
meson interacts with a proton of the liquid inside the bubble chamber. The K
beam
was selected with the techniques described in Chap. 3. The final state consists of two
7.4 Low Energy Hadron-Hadron Collisions 145
charged and one neutral particle. The neutral one decays into two charged particles.
The event is consistent with the following hypothesis:
K
p !
0
C
,!
p:
(7.12)
This first reaction corresponds to the production of two charged pions and a
0
;the
0
then decays into a proton and a
meson.
However, one can imagine that the reaction (7.12) proceeds through an interme-
diate process, with a much higher probability (i.e., cross-section). In this second
hypothesis, two new resonant states (each of which represents a new particle)are
formed. These resonant states are called ˙
˙
.The˙
˙
, depending on the sign,
decay into
0
C
or
0
; these new reactions yield the same final state as in
(7.12) through the sequence
K
p ! ˙
C
or K
p ! ˙
C
,!
0
C
,!
0
,! p
,! p
:
(7.13)
If this is indeed the case, the mass of the system
0
C
, obtained in (7.13) “peaks”
at a value corresponding to the mass of the new ˙
C
resonant state (the same for the
˙
). To test the hypothesis, many events, for example, the one shown in Fig. 7.4,
must be found and measured. It is necessary to have several photos similar to this
(it is not difficult since this process is governed by the strong interaction, and the
production is abundant). The kinematic variables which can be measured (assuming
that the proton and pion masses are known) are the charged particle momentum and
the emission angles between them.
The “effective mass” of the (
0
C
) system in the final state is (c D 1)
m
2
0
C
D E
2
0
C
p
2
0
C
(7.14)
D .E
0
C E
C
/
2
.
!
p
0
C
!
p
C
/
2
D E
2
0
C E
2
C
C 2E
0
E
C
p
2
0
p
2
C
2p
0
p
C
: (7.15)
Remember that E
2
0
p
2
0
D m
2
0
, E
2
C
p
2
C
D m
2
C
. In addition, one
has p
0
p
C
D p
0
p
C
cos #
,where
is the angle between the emission
directions of the
0
and of the
C
.From(7.15), one obtains
m
2
0
C
D m
2
0
C m
2
C
C 2E
0 E
C
2p
0 p
C
cos
: (7.16)
The
0
and
C
momenta are measured by the curvature radius of the particle in the
magnetic field. The energies E
0
and E
C
are obtained from the masses and the
measured momenta, E
2
0
D m
2
0
C p
2
0
, E
2
C
D m
2
C
C p
2
C
.
A “trick,” due to Dalitz (1953), helps to demonstrate the existence of a resonant
˙
˙
state, quickly decaying into
0
C
or
0
. The invariant mass (7.15)
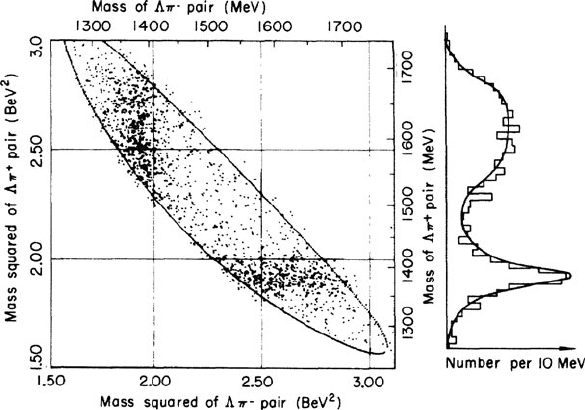
146 7 Hadron Interactions at Low Energies and the Static Quark Model
Fig. 7.5 Two-dimensional diagram (called Dalitz plot) of K
p !
0
C
events for incident
K
of 1.22 GeV/c momentum. Each measured event is represented with a dot in the plot. The
solid line delineates the available phase space, that is, the region of values allowed by the energy
conservation. The mass distribution of the
0
C
is also shown as a projection along the y-axis:
note the peak at 1,385 MeV corresponding to the ˙
C
particle mass. The structure near 1,600 MeV
is a “reflection” of the
resonance, peaking at the mass 1,385 MeV along the x-axis (not
shown) [7S63]
measured on each of many recorded events is plotted along one axis of a two-
dimensional graph (scatter plot). For the second axis, the value of the similar
invariant mass of the
0
system is used. If a resonance is formed (i.e., a particle
with defined mass and quantum numbers), one would expect to find a clustering of
points in the plot.
Figure 7.5 shows the Dalitz diagram (Dalitz Plot) for K
p !
0
C
events.
A horizontal concentration of events corresponding to m
C
D 1;385 MeV and
a vertical concentration corresponding to m
D 1;385 MeV are clearly visible.
The projection along the y axis is also shown. Note the peak at m
C
' 1;385 MeV
and a broader peak at ' 1;600 MeV. The latter is caused by the presence of the
clustering of the m
' 1;385 MeV (it is a so-called “reflection”). The structure
at m
C
D 1;385 MeV corresponds to the ˙
C
(1385).
From Fig. 7.5, it can be deduced that about half of the events of reaction (7.12)
produces
0
C
pairs with a peak at mass 1,385MeV; this means that in 50% of
the cases, the reaction occurs through ˙
C
(1385), giving rise to the chain of events
described in (7.13). In the bubble chamber, the state ˙
C
(1385) cannot be seen
because it has a very short lifetime, of the order of 10
23
s, typical of a hadron
which decays through the strong interaction.

7.4 Low Energy Hadron-Hadron Collisions 147
The lifetime of the state can be estimated using the peak width shown in the
projection along the y-axis in Fig. 7.5. The typical width of these states is
100 MeV. From the uncertainty principle, one can write
'
„
D
6:6 10
22
MeV s
100 MeV
D 6:6 10
24
s 10
23
s:
The ˙
C
(1385) is a state with well defined mass, electric charge, spin and others
quantum numbers. However, because of the short lifetime, it seemed difficult to
call them “a particle.” For this reason, and because of the mathematical form of the
cross-section as a function of energy described in the next paragraph, these short-
lived particles were called resonances.
Clarifications regarding the uncertainty principle. The uncertainty principle
tells us that in Nature, a limit exists on our possible knowledge of the
submicroscopic world, e.g., regarding the dynamics of a particle. For pairs
of conjugated physics variables, for example, energy and time, momentum
and position, there are limitations in the precision of their measurements. For
example, if we measure the position x of an electron with a precision x,we
cannot simultaneously measure the p
x
component of its momentum with un-
limited precision. According to the uncertainty principle, an uncertainty p
x
related to the uncertainty x exists. Similarly, E and t are related through
the uncertainty principle. In the literature, different numerical expressions for
the uncertainty principle are used, that is,
E t
„
2
; „ ; h
p
x
x
„
2
; „ ; h:
From a theoretical point of view, the first expression is better justified
.E t „=2, p
x
x „=2/, because it can be directly derived
from (1) the commutator algebra, (2) the analysis of the wave functions
structure, (3) the quantum harmonic oscillator ground state. This implies
that the uncertainties E; t; x; p
x
have the meaning of standard
deviation, i.e., the mean squared error at the 67% probability. In the case of
the energy (mass) width of a resonance, we can consider that E D =2, i.e.,
the half-width at half-maximum, as coinciding with one standard deviation.
For this reason, the quantity is expressed in MeV (the quantity
i
= is
dimensionless, and expresses the decay probability in the ith channel). For
decay processes, one uses t D D lifetime of the particle at rest. Finally,
one can write
E t '
2
„
2
) „: (7.17)

148 7 Hadron Interactions at Low Energies and the Static Quark Model
In the considered hadronic resonance, ' 100 MeV, yielding to '
0:66 10
23
s. For a resonance of mass m produced with kinetic energy E,the
lifetime is relativistically increased by a factor of D E=m, and D
rest
.
7.5 Breit–Wigner Equation for Resonances
Consider the collision between two hadrons: the incident particle corresponds to a
wave function with de Broglie length ¯, the second hadron is at rest in the laboratory
system. The energy of the incident particle can be varied. If, at some value of ¯ and
for a particular value of the relative angular momentum ` between the two hadrons,
the cross-section passes through a maximum, one can say that there is a hadronic
resonance. The resonance is characterized by
• Defined angular momentum J D ` (for spinless particles).
• Defined parity.
• Defined value of the isospin I .
• Defined mass, equal to the total energy in the center of mass at which there is the
resonance maximum.
• Defined lifetime, as determined by the width at half-maximum ( )ofthecurve.
A resonance implies an increase of the formation probability W (4.28). Figure 7.5
shows a concentration of events in the energy region around 1,385 MeV. An
enhancement of the number of produced events, and consequently of W , with a bell-
shaped distribution as that seen along the y-axis projection of the figure, involves
a similar increase in the production cross-section ( ' W ). In the following, we
shall derive the equation of the curve, called the Breit–Wigner (BW) equation.The
typical BW shape is plotted in Fig. 7.6. Note that the resonance energy E
R
,which
corresponds to the mass of the resonance, coincides with the peak of the function.
However, the width is defined as the difference in energy between the two points
where D
max
=2 (full width at half-maximum).
Fig. 7.6 Shape of the
Breit–Wigner equation. is
the width of the curve at the
ordinate point where
D
max
=2
0.5
1.0
E
R
E
σ/σ
MAX
Γ
