Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

второго п третьего способов. Что касается четвертого способа

то он может иметь значение при некоторых исследованиях и эксое'

рнментах. На производстве этот сиособ в настоящее время не ори-

меняется.

Учитывая сказанное, приведем примеры только второго и третьего

способов уравнивания. Что же касается первого и четвертого спосо-

бов, то ограничимся лишь изложением их теории.

1. Двухгрупповой способ Гаусса

Этот способ заключается в следующем. Условные уравнения раз-

бивают па две группы и под условием \рг-\ — пип решают сначала

уравнения I группы, откуда иаходят первичные поправки

и вводят их в пзмерепные величины. Окончательные значения по-

правок получают как суммы

(VI П.«

где ^ — вторичны е поправки, для отыскания которых всю

заданную систему условных уравнений решают совместпо под усло-

вием !р

*•>"*)

= лип, При этом свободные члены уравнении II группы

вычисляют с результатами измерений, исправленными первпчнммп

поправками ь?,'. Очевидно, что с исправленными результатами изме-

рении свободные члены I группы будут все равны нулю.

Покажем правомерность такого решения па примере четырех ус-

ловных уравнений, разделенных на две груниы, по два уравиеипя:

(VII 1.2)

Выразим поправки через коррелаты. т. е. напишем корреллт-

иые уравнения поправок, решив все уравнения (VIII.2) и (VIII.3)

совместпо.

\Т

012^1

+ + .

. . /VIII А\

С1

= —

..., п). (\ 111.4)

Решим теперь уравнения I группы отдельно под условием \ри'"\ =

= тпш п найдем из этого решения первичные поправки Обозна-

чив коррелаты отдельно решаемых уравнений I группы через к\ н

напишем

ел*?-' «.»*$

=——=• о-ш.5)

Выразим коррелаты /с, и к

через приближенные значения к\.

к\ н поправки к ним

282

н подставим эти выражения в формулу (VII

1.4).

Получим

ЯмЛА-,

4- <чМ

-}. а

л-,

«7= г: 1 Г— '

Р1

или с учетом выражении (VIII.."»)

где

а/

ЛА'

ОЦ^х

—

(»=* 1

и).

(VII 1.6)

(VII 1.7)

Отсюда видно, что для получения вторичных поправок и] нужно

решить нормальные уравнения с неизвестными коррелятами б/г,.

и Матрица коэффициентов этих нормальных уравнений

будет та же, что и для уравнений I и II групп, но свободные члены

будут отличаться, а именно в I группе уравнении это будут нули,

а во II группе — некоторые неизвестные нам цока значения XV%

и Таким образом, имеем

бА

+ (да^)

[?4,я

]

~ [А, +

(1<Г«л1 А?

+ + О

А?

+ [дс

] + И',) -

6А-!-}- [?«

] бА-

+ (?о

оз1

*з-г[уо

а,] А\,+

+ +

Ао

+ 1У

) = О

(дя^^!

[<7а

]

б/с

+ А-з+('?'»1"1-т

Ч-

(1?в

А®

г И',)

—О

На основании (VIII.5) легко видеть, что свободные члены (в круг-

лых скобках) первых двух уравнений (VIII.?) равны пулю. Рас-

смотрим теперь свободные члены последних двух уравнений (VIII.7).

Эти свободные члены можно получить как невязки, если пользо-

ваться исправленными после первого уравнивания рсзультатад>и

измерений. Обозначим новую невязку третьего уравнения через И','

и вычислим ее указанным выше путем

И'з=(*1 К

*п)-

(VIII .8)

Разлагая в ряд эту функцию и ограничиваясь линейными членами

разложения, получаем

\У'

фз (*! '•; \-*я + г'

) -ч-з('|.

т. е.

• <>Ф8 , , . .

- ' '"» = »

-г-«-

Получим значение \а

и\ из равенств

(VI

11.5)

V'. -

</,«„А°-г О^

")•

м +

• Г^пз'',','

(VIII.!))

283

Теперь (У111.9) примет вид

т е. свободный член третьего уравнения системы (VIII.?) можно

получить по формуле (VIII.8), что и требовалось доказать. Анало-

гично можно показать, чго

= (*!+»;, • • + О'ПМО)

Нгак, в двухгругшовом способе Гаусса поправки нужно вы-

числять как суммы

*>1

•=»}+*> г

где первичные поправки щ находят пз решения системы условных

уравпений (УШ.2), а вторпчные V] — по формуле (VIII.С), где 6/^,

бк, к

и находят из системы нормальных уравнений

[7«»«д!

б^-Мдвл!

з]

А"з +

|9Я1«41 *4

+ [у

/г

]

[-70

в4] А,

[(^яз) 6А-,

-+- [7«

«з1

Г«7°зОз1

Аз + ] + IV

[едо^&Ч + ^од]

бА-а-Ь[дя

]

Лз +

|0л

а|] *4

+ = 0 ,

а свободные члепы И з и

IV.!

— нз условных уравнении (первоначаль-

ных, не приведенных к линейному виду), пользуясь результатами

измерепий, исправленными первичными поправками, по формулам

(VIII.8) и (УШЛО).

Таким образом, правомерность двухгрунпового способа Гаусса

доказана. Этот способ может дать некоторую выгоду по сравнению

с обычным способом лишь в том случае, если I группа условных

уравнений распадается на независимые уравнения л поэтому решается

просто. Тогда упрощаются действия в графе IV схемы решения иор-

мальных уравнений коррелат.

Как указано в начале параграфа, двухгрупповой способ Гаусса

необходим для обоснования изложенных ниже способа приближений

и способа Крюгера.

2. Способ приближений Гаусса

Исходя из рассмотренного выше способа, К. Ф. Гаусс предложил

способ приближений для решения условпых уравпений. Как уже го-

ворилось, в двухгрупповом способе сначала отдельно решается

^группа уравнений (УШ.2), откуда походят первичные поправки

о], а затем вычисляют вторичные поправки и] из совместного реше-

ЕИЯ условных уравиешш:

I группа

ТТ [02^1 = 0

II г р у п п а

где И'з и IVI вычислены по формулам (VIII.8) и (УШЛО).

284

(VIII. И)

М1В

М22

•6,125(1

Рассматривая систему условных уравнений (VIII.11) как исход-

ную. вновь применяем к ней двухгрупновой способ Гаусса.

Так как в I группе уравнений

(VI

11.11) все свободные члены

равны нулю, то отдельное решение этих уравнений никаких изме-

нении в поправки не внесет. Поэтому сначала отдельно решают II

группу уравнений (VIII. 11), т. е. уравнения

М + И^О.

1$ результате получим третьи поправки, после впесепия которых

появятся невязки И'! и И''», но исчезнут невязки 1У

' и

Продолжая этот процесс, т. с.

решая поочередно группы услов-

ных уравнений, постепенно умень-

шаем невязки. После ликвидации

всех невязок решение заданной

системы условных уравнений за-

канчивается. Так как каждая ре-

шаемая в процессе прнближеппй

система уравнений равносильна

предшествующей н уточняет зна-

чения искомых поправок, то най-

денные в приближепиях по-

правки VI, и'Г и т. д. должны

дать в сумме для каждой измерен-

ной велпчппы х, искомую по-

правку т. е.

где 5 — число приближений, при

котором все невязки окажутся лик-

видированными. В §

1Г)

доказана сходимость указанного процесса

приближении.

Каждую из двух груин уравнении, в свою очередь, можно под-

разделить для решения еще на две группы и вообще делить условные

уравнения па любое число групп. Наиболее ъыгодиым разделением

является такое, при котором групиы распадаются на иезависс.иые

уравнения.

Проиллюстрируем способ приближений Гаусса па примере. Для

этого возь.мем пример 1 § 69.

П р и м е р. На рис. 1С направления звеньев * выбрапы с таким расчетом,

чтобы в условных уравнениях все коэффициенты были равны +1.

Условные уравпенпя разделим на три группы следующим образом:

1 группа

ч>.

* Стрелка па чортежо указывает на пункт, высота которого является умень-

шаемым в измеренной разности высот (превышении).

285

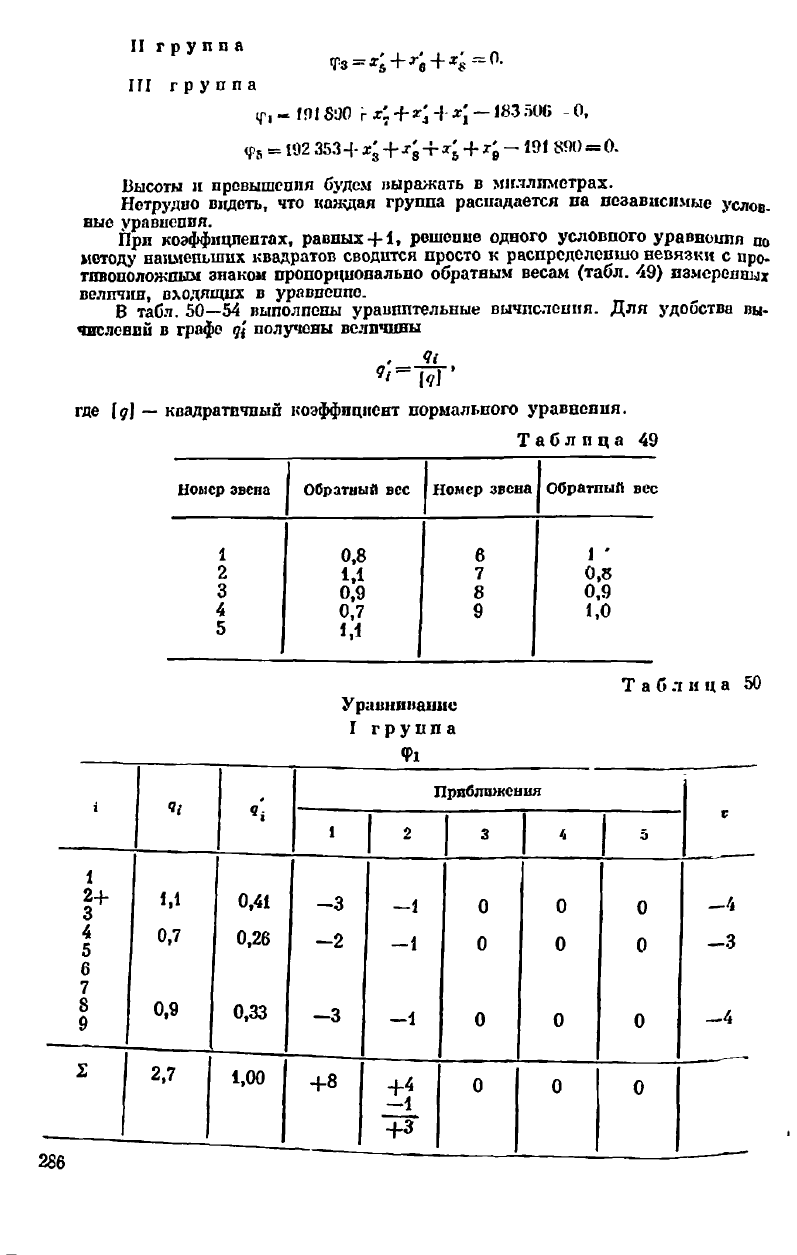
II группа ,

Ъ = + +

Ш группа

«Г,

!!»!

890

4 + + -

183 50<;

192

353 Ч-+ +

191 890

Высоты и провышспня бз'дем ныражать в миллиметрах.

Нетрудио видеть, что каждая группа распадается па независимые услов-

ные уравнения.

При коэффициентах, равных+

решение одного условного уравнения по

методу наименьших квадратов сводится просто к распределению невязки с про-

тивоположным знаком пропорционально обратным весам (табл. 49) измеренных

величин, входящих в уравнение.

В табл. 50—54 иыполпены уравнительные вычисления. Для удобства вы-

числений в графе получены величины

где [д] — квадратичный коэффициент нормального уравнения.

Таблица 49

Номер звепа Обратный вес

Номер звена

Обратный вес

0,8

1 '

1.1

0,5

0,9

0,7

1,0

1,1

1,0

Т а

л и

ц а

Уравнивание

I группа

Ф1

Приближения

1 1

3 4

1.1

0,41

-3

—1 0 0

—4

0,7

0,26

-2

-1 0

—3

0,9

0,33

-3

—1

-4

2,7

1,00

286

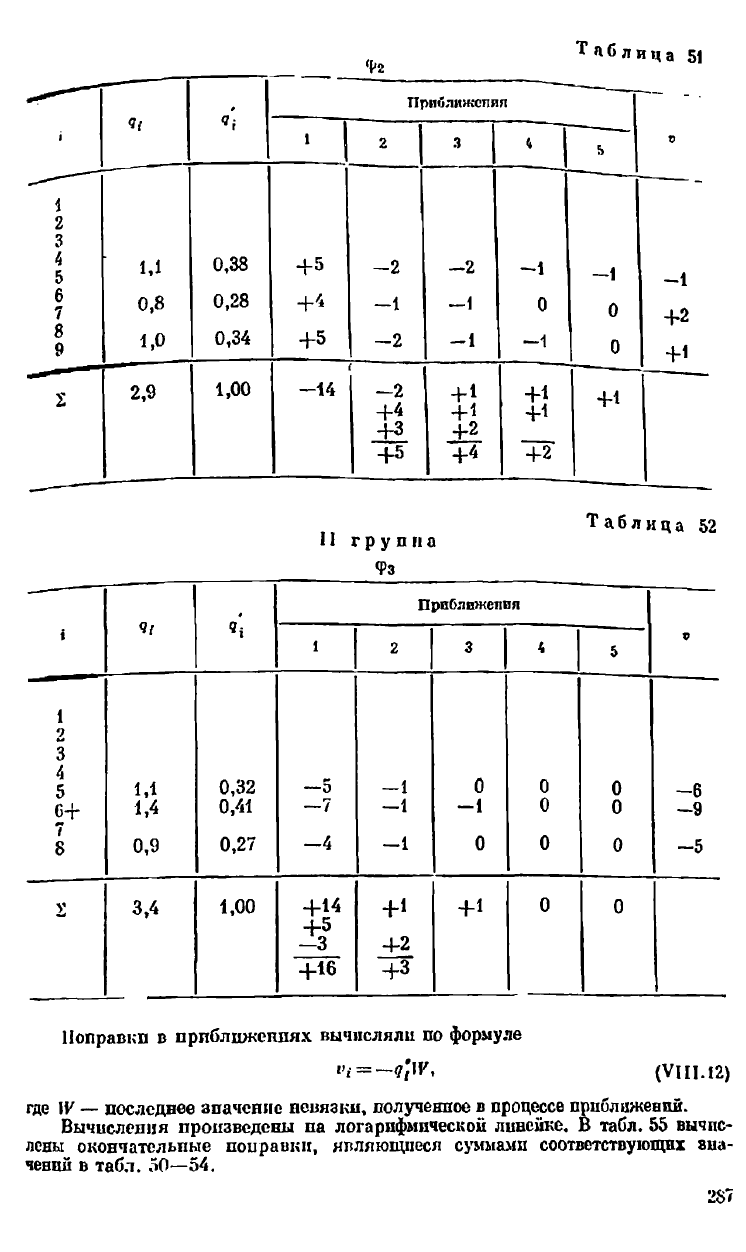
Таблица 39

Приближения

1,1

0,38 +5

-2

—2

-1

0,8

0,28

-1

1,0

0,34

-2

-1

—1

2,9

1,00 -14

—2

+ 1

—1

-1

II группа

Фз

Таблица 52

Прпближслпя

•

3 4

С4-

1,1

1,4

0,32

0,41

—5

—7

-1

—1

-1

-6

-9

0,9

0,27

—4 —1

0 0

-5

3,4

1,00

+14

+16

Поправки в приближениях вычисляли по формуле

= V,

(VIII.

12)

где

1У

— последнее значение пенязки, полученное в процессе приближений.

Вычисления произведены па логарифмической линейке. В табл. 55 вычис-

лены окончательные пои ранки, являющиеся суммами соответствующих вна-

ченнй в табл. 50—54.

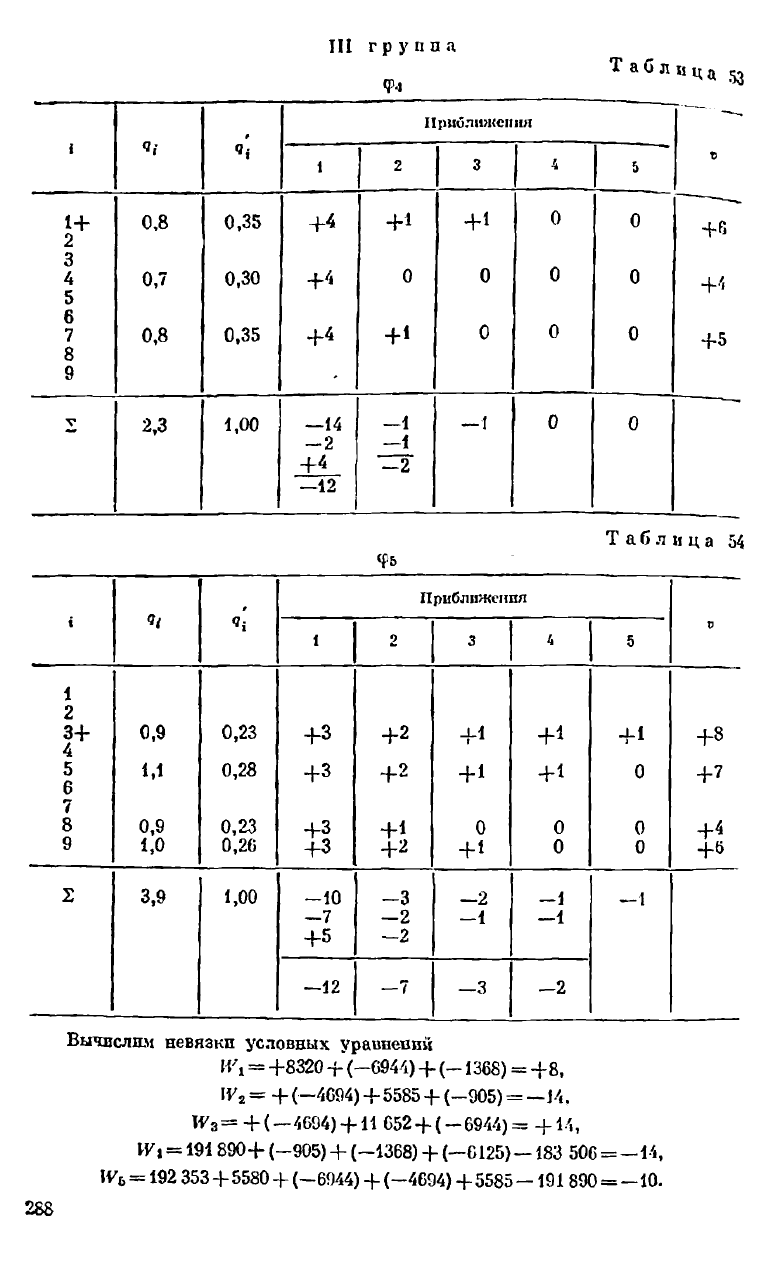
III группа

Таблц

Ца

0,8

0,7

0,8

2,3

0,35

0,30

0,35

Приближения

1,00

—14

—1

-2

—1

-2

—12

4>ь

Таблица 54

Приближения

0,9

0,23

+з

1,1

0,28

+ 1

0,9

1,0

0,23

0,20

+з

+ 1

3,9

1,00

-10

—7

-3

-2

—2

—1

-1

—1

— 1

—12 —7 —3 —2

Вычислим невязки условных уравнений

И'*1

= +8320 + (-0944) + (-1368) = +8,

И'

= +(-4094)4-5585 +(-905) = —14,

И'з = + (—4694) + И 052 + (-6944) = +14,

И', = 191890+ (-905) + (-1368) + (-С125)—183 506 =

\У

= 192 353 + 5580 + (-6944) + (-4694) + 5585 -191 890 =

-14,

-10.

288

а б

лица 55

' • I

5 8

— —

4-6

, ,

•>

— Ч

—

—4

—

—3

—

—1

—6

—

— —

—«)

—

—9

—

—4

— —;>

44 -5

+ 1

—

ал;

Примечания к табл. 50—54.

В графе I знаком «плюс» выделетл номера звеньев, входящих только

в одно уравнение. Поправки в соответствующих строках не изменяют невязок

других условных уравнении.

В последних приближениях, когда число миллиметров остаточной непязки

меньше числа поправок, эти поправки в первую очередь следует

впоепть в

звепо,

выделенное «знаком плюс».

Подставим пацдешше значеппя поправок в условные уравнения попра-

вок

Ф,

= "г+

'в + -И^! = —- 5-г

1-'г

8=0,

Фа

«?ь+

«•'»+И'

=0+7 + 7

—14

Фз = «ъ -Ь "6+ г

И'з

0-9 -5 414 - 0,

Ф>4

= ^7-г '1-Ь1-1+

И'4

+74 I ,

-14 =

о.

Фг,

= +

'в

+ 1'Б +' 'в +

= +8 - 5 + 0+7 -10=0.

Полученные окончательные попрании в превышения отличаются от попра-

вок в примере 1 § 69 в пределах 1,5 мм.

Вычислим высоты реперов

183.506 -

(-6.125

С™)

= 189,625 = //

192.353+ (+

Г>.Г>80+8мм)

197.941

= //„,

191.890 + (-0.905 +

ММ

)

= 190,902=У/

191.890

+ (5.585 +

7ш»)

= 186.298=Яве

Высоты также сошлись с томи, которые получены в примерах

§ С7

и 69,

в пределах 1,5 мм.

Таким образом, мы убедились в практически достаточной строгости способа

приближений Гаусса.

3. Способ Крюгера

Способ Крюгера, так же как и способ приближений Гаусса, яв-

ляется развитием двухгруппового способа Гаусса. Сущность способа

Крюгера заключается в следующем.

Условные уравнения поправок делят но два группы, после чего

выполняют уравнивание с учетом уравнений I гр\шш, и результаты

измерений исправляют первичными поправками. Далее, пользуясь

19 Заказ ШО 289

исправленными результатами измерений, вычисляют невязки ц

группы.

Попутно с решеппем I группы нормальных уравнений находят

при помощи донолнптельпых граф так называемые переход,

н ы е м ножители, На этом заканчивается первый этап урпв.

нивапия. который отличается от первого этапа уравнивания двух,

групповым способом Гаусса только действиями по нахождению пере-

ходных множителей.

На втором этапе уравнивания вычисляют прп помощи переходных

миожптелей новые коэффициенты условных уравнений поправок

II группы, позволяющие ограничиться решением уравнений толь-

ко II группы и получить окончательные значения вторичных по-

правок.

Таким обравом, в способе Крюгера вместо общей системы нор-

мальных уравнений приходится решать две системы с меньшим чис-

лом уравпений и в отличие от способа приближений Гаусса только

но одному разу.

Рассмотрим теорию способа Крюгера. Имеем пять условных урав-

нений поправок, которые разделены на две группы следующим

образом.

I группа

М + и^о.

[д

»]-гИ'

=0,

(о

г'1+И/

=0,

II г р у и п а

[«!«>]

+И', = О,

(с^ + И^-О.

После первого этапа уравнивания и исправления результатов

измерений можно запасать, как указывалось выше, следующую си-

стему условных уравнений поправок.

I г р у п и а

]0,!»Ч

[«^"1=0,

II группа

где [VI и И^' вычисляют с исправленными результатами измерений.

Заменим теперь коэффициенты условных уравнений поправок

II группы, т. е. а

, а

, новыми коэффициентами А

, А

(г = 1,

. . . , п), подобранными так, чтобы общая система нормальных урав-

пений распалась на две независимые системы. Очевидно, что коэффи-

циенты А должны быть некоторыми линейными функциями коэффи-

циентов а и а.

290

Допустим, что преобразовании сделаны ц получена следующая

система условных уравнений:

I группа

К»"] о

[«•,<<•4=0

II группа (преобразованная)

('1 4

И",

[Л,»*14 1г; =0

(VIII.

13)

На основе системы условных уравнении (VIII.

13)

можно написать

систему нормальных уравнении

(

\ 6*!-!-

(дадОа) 6А-

+ А*а4- 1?в,Л к\ 4 [^Л

] к'

[дя^а!

Ьк

+ [?а

] 6А

4- [^«г!

^А'3

4 [<7 V*к\ г

[<7М

]

к'

ДОде)

бА

1?о

] бА-

4 [<?«

] бА-

4(9"аЛх1 А<

[<7М

] к'

-0

,1 6А-, 4[Ч^Ау]

бА-

+ ,1<№

(?Л,Л

]

к\

4[<И,Л

к'

+ • (VIII. 14)

4-^=0

[да,Л

] Ьку

4 ко

]

бА-

4 [4«

.-1

] Лк

4 (<7 Л

^1,1

к\ г

17-М

] А-^4

Для того чтобы система (VIII. 14) распалась на две независимые

системы, поставим следующие условия:

(7«*Л|1=0 ,

(VI 11.15)

\<ЧЬА\\ -0 .

1<7

1Лг1=0

№«Иг)=0 -

(VIII. 16)

[до

Ло]=0

Отсюда видно, что для решения задачи требуется определить

шесть переходных множителей, а в общем случае г,-г

множителей,

где г

— число уравнений в I группе, г

— во II группе.

Из шести переходных множителей три потребуются для вычис-

ления коэффициентов А

и три — для коэффициентов А

(г =

= 1, . . п). Напишем для коэффициентов Л

равенства

Ац=ац Рп + Я/гРа + в/зРЗц + ал

. . ., л),

(VIII. 17)

где р — переходные множители.

Умножив каждое из равенств (VIII.17) соответственно на

ац

п сложив их, нолучим

\ца

= (да^] Рц-Н^с,) р

4-[?а,а

)

1ва

Используя аналогично коэффициенты а

(г

и а,

, получаем

[да

Л,]

[чауаД

(</«

] р

4" 1?о

)

,4 (да^],

19(13-1^

= 1да

) р

4 [?а

1 (>

,4№«заз] Р314 [9азочЬ

19* 2»!