Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

асяство (Ш.5) перепишем

т*«т|+т$ (111.7)

О I о

Средняя квадратпчсская ошибка одного измерения т чарактери-

совместное влияние на него т

- случайных ошибок и влия-

це т ~~ систематических ошибок измерений.

На оснований формулы (Ш.З) приближенное значение средней

1чвда

т1ческой

ошибки т можно вычислять но формуле

| *«

т & | (III.9)

где V — число равноточных измерений величины X.

Приближенное зиачение величины т

можно получить ио формула

™д=Г ' (111.10}

где — отдельные измерения, 1=1.2, . . . , п:

- 1-1

Для 7н& основании выражения (Ш.7) можно написать

т.

«/^-Щу (III.11;

Вопросы определения величин т, н т^ являются одпнмп па

основных в теории ошибок измерений.

Средняя и вероятная ошибки и их связь

со средней квадратической ошибкой

Кроме основной характеристики /и

, характеризующей влпяни<?

случайных ошибок на результаты измерений, ппогда применяют до-

полнительные характеристики, а именно среднюю о ш п б к у

в вероятную о та п б к у.

Средней ошибкой Ф называется математическое ожида-

ние абсолютных значений отклоиений| результатов пзмерелпй какой-

либо величины от математического ожидания для этих результатов.

т. е.

=-1/(151).

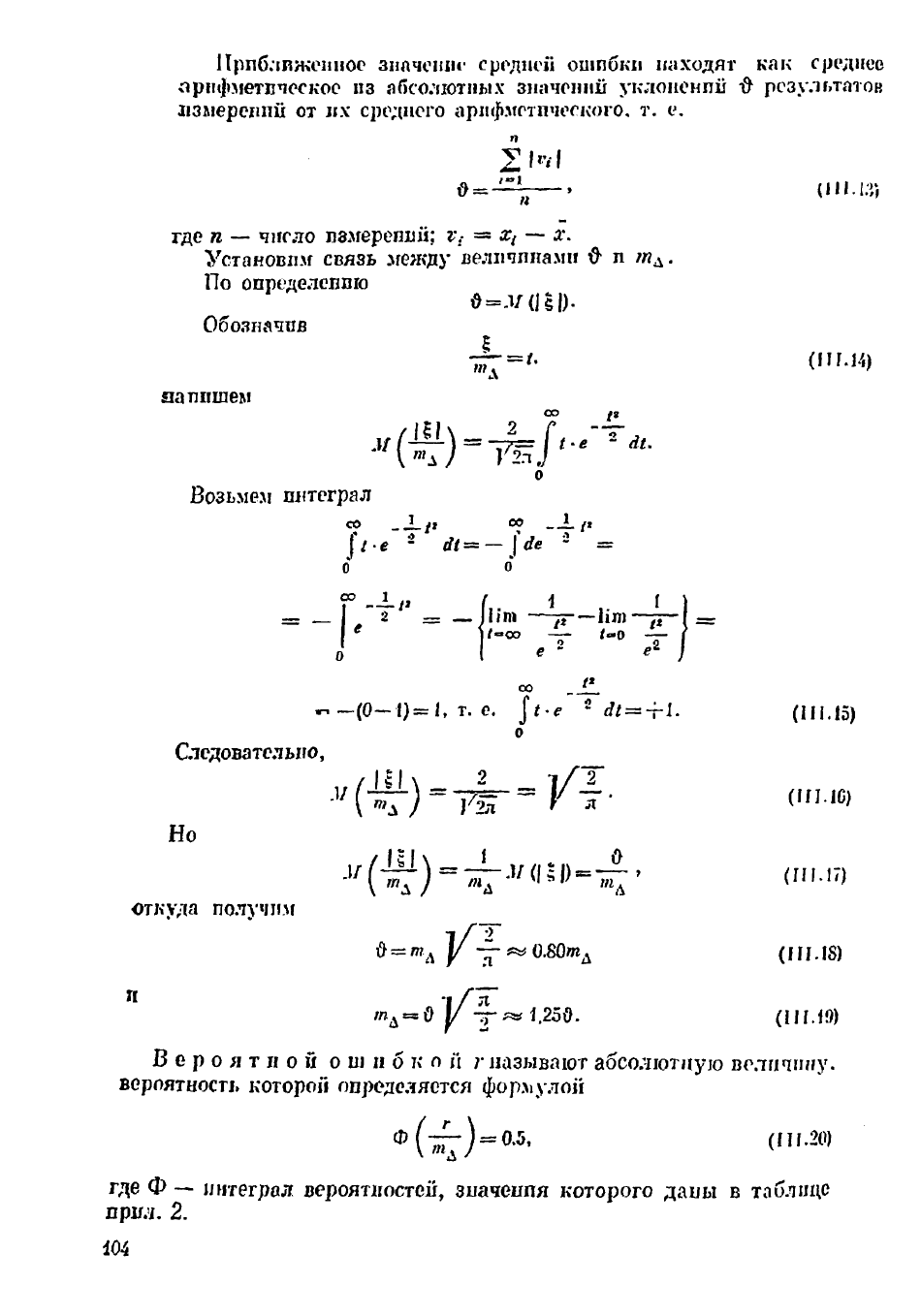
Приближенное значение средней ошибки находят как среднее

арифметическое из абсолютных значений уклонений Ф результатов

измерений от их среднего арифметического, т. е.

2>«1

0 = —» (Ш.1.Г,

где п — число измерений:

т.

= х

—-

х.

Установим связь между величинами д и /н

По определению

#=-1/(15 !)•

Обозначив

("М4)

запишем

со Iг

Возьмем интеграл

со

/<•

-•г"

со 1

- /А -

со

1'"

[|»П1

1/-00 —

—1ш

<-0

0 1

! е

1Д-) ^ ,

--(0-1)=1, т. е. ^1-е

Л = -Ы. (III.15)

Следовательно,

/1е1\ 2 |/Т

Но

д = т

^ 0.80т

(III.

18)

1.250. (111.19)

Вероятной о ш и б к о й г называют абсолютную величину,

вероятность которой определяется формулой

где Ф — интеграл вероятностей, значеппя которого даны в таблице

прил. 2.

№

откуда получим

Потенцированием по величине Ф (/) =

0,5 получаем

——

0.6745

. . .,

0ТК}'Л

г 0,67т

. (111.21)

Приближенно вероятную ошибку можно получить следующим

образом.

Уклонение результатов измерений от среднего арифметиче-

ского располагают в ряд по возрастанию абсолютных значеппй

После этого величина | 1, находящаяся в середине этого ряда, бу-

дет приближенным значением вероятной ошибки г'. Это следует и»

формулы (111.20), если вероятность заменить относительной часто-

той. Если чпело наблюдений четное, то г' получают как срсдпсе из

двух величин расположенных в середине ряда. Величину г'

полученную указанным эмпирическим путем, называют еще сре-

динной ошибкой.

Соотношения (111.18) и (III.21) чисто теоретические. Степень со-

блюдения этих равепств зависит от числа измерений и является од-

ним из признаков соответствия действительного распределеппя нор-

мальному. так как интеграл вероятностей взят для нормального

распределения.

§ 31. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ОШИБКИ

Абсолютными ошибками называют среднюю квадра-

тическую га, среднюю Ф, вероятную г, истинную Ф.

Относительной ошибкой называют отношение соответ-

ствующей абсолютной ошибки к полученному значению измеренной

величшш .Относительную ошибку обычно выражают в виде

дроби с числителем, равным единице. Относительную ошибку опре-

деляют по соответствующей абсолютной ошибке.

Пусть х — полученное значение некоторой величины.

Тогда

Я» 1 „

— —

^ средняя квадратическая отпоептедьиая ошиока этой величины;

— -д?

средняя относительная оппюка:

—

у вероятная

гвосительная оишока;

пстпнпая отпоептельпая опгпока.

Знаменатель относительной ошибки целесообразно округлять до

Двух зпачащнх цифр с пулями.

105

Примеры.

I .

0.25

я, х—196,0 м; — тзу"»

=ОЛ7 м, х=Ш,5 м; — 2800"'

=0.037 м. а:=810,314 м; ~ 22 ООО''

§ 32. ОЦЕНКА ТОЧНОСТИ ПРИБЛИЖЕННОГО ЗНАЧЕНИЯ

СРЕДНЕЙ КВАДРАТИЧЕСКОЙ ОШИБКИ т

Рассмотрим вопрос опенки точности приближенного значения

средней квадратпческой ошибки в зависимости от числа измереппп п

Обозначим:

— искомое зпачепие средней квадратпческой ошибки приближен-

ного значения т

;

т* — псгинпое значение средней квадратической ошпбкп, соответ-

ствующее далным условиям измерений;

<т

— приближенная средняя квадратическая ошибка, вычисленная

по дапным результатам п измерений.

Истпнпая ошибка величины т

Д«

=т

—и®.

Эта ошибка будет случайной, так как

На основании определения (III.3) напишем

или

= и(т1)-2т1т1 + т**~м{т1)-т**, т. е.

Предположим, что значения т

вычисляли по формуле

(111.19)

2161»

я* 1.250 1.25 — .

106

ТоП

(П1.22) можно переписать

т* 1.2523/ (02)_,„о-.

# о

(П1.23>

)

—

Войдем

т. е.

- (Б?) +

2 (.V

I 5

и м Ъ

* И - «

•

"'К

1-1 1-1 \ /-/•! /

4-2 У(л/|6|| У -V |

1Л

.-1 \ ьП-1 )

Теперь равепство (111.23) примет вид

< =* 25= -1- {

пт

+ п {п

}

#2}

= 1.25

и —

а принимая во внпмапие выражение (III.19),

Заменяя неизвестное нам значение иг® на его приближенное зна-

чение получаем

«,.1.252 — + т\- т\ =

то « п п д <\

т:

= -(1.252-1),

т. е.

Йлц

т? =

У.56тд

т п

0,75т.

/Ит

(И 1.24)

107

Приближенно

П1

гпт ' СП.25)

» 2я '

В практике часто пользуются формулой (111.25). Мы будем иеиоль-

зовать более точпую формулу (III.24). При л ^ 20 формула (III.24)

позволяет установить доверительные границы сразу для стандарт л,

не вычисляя их предварительно для дисперсии, как это сделаьо

в §21. При этом пользуются нормальным законом распределения.

Д.чя примера, приведенного в § 21, получим

0.75x0,253

Мв

"" Уто ~

0,0423

Доверптельпыми границами при (5 =0,8 (т. е. I = 1,28) будут

0,253—1,28X0,0423=0,253—0,054 ««0,20

0,253+0,054 *»0,31.

Практически получен тот же ответ, что п в § 21.

Однако при п < 20 следует пользоваться распределением у-

(см. § 21).

Формулу (111.25) используют для определения необходимого

числа значащих цифр в вычисленном значении а' п тд. Так, напри-

мер, если приближенное значение стандарта от' — 1,66 получено пз 50

наблюдений, то т

- -•== = 0,17. Очевидно, что пот смысла для

о' сохранять сотые доли и следует писать о' = 1,7. Заметим, кстати,

что почти во всех случаях практики для приближенного значения

стандарта и для средней квадратпческой ошибки достаточно со-

хранять две значащие цифры.

§ 33. ИССЛЕДОВАНИЕ РЯДОВ ИЗМЕРЕНИЙ

Для определения точности результатов измерений и закономер-

ностей распределения их ошибок, нолучешшх в тех пли ппых усло-

виях, проводят исследования рядов измерепин. Прп этом ставится

эксперимент пли анализируются результаты производственных

работ.

Исследуемый ряд измерений может относиться как к многократ-

ным измерениям одной величины, так и к измерениям нескольких

однородных величин, выполненных примерно в одинаковых условиях.

Конкретными задачами исследования ряда измерений являются,

во-иервых, отбраковка грубых измерений, во-вторых, определение

точности одного измерения и, если возможпо, характеристик систе-

матических влияний и, наконец, определение критериев согласия

с иормальиыы распределением. Заметим, что первая и вторая задачи

тесио связаны между собой.

Полное исследование рядов измерений имеет смысл лишь при

наличии достаточно большого числа результатов, во всяком случае,

108

прп их числе п ^ 50. При п < 50 можно решить лишь част лыс задачи

„^следования.

Если истинные значения измеренных величии пеизвестиы, то из

исследования ряда измерений можио вынести суждение о влиянии

;

(

ншь случайных ошибок, параметры которых характеризуются укло-

нениями результатов измерений от среднего арифметического. Влия-

ние же систематических ошибок в этом случае полпостью выявить

нельзя.

Еслп истинные значения измеренных величин известны, то про-

водят исследование ряда истинных ошпбок измерений, которое рас-

смотрим и первую очередь.

Для выявления измерений, содержащих грубые ошибки, необхо-

димо знать среднюю квадратическую ошибку т одпого измерения

где — средняя квадратпческая ошибка, характеризующая влия-

ние случайных ошибок;

— средняя квадратпческая ошибка, характеризующая влия-

ние систематических ошибок.

В этом случае применяют правило утроенной средней квадратн-

пеской ошибки (правило «трех сигм»), по которому ошибки, превы-

шающие но абсолютной величине Зт, следует считать грубыми. Зна-

чение Зт называют предельной допустимой о ш и б -

к о И. Еслп средняя квадратпческая ошибка т пеизвестна. то для

выявлепия грубых ошпбок поступают следующим образом.

1. Вычисляют среднее зиачеиие 0 пз ряда истинных ошпбок 0

2 О,

0 = = 2, .... п)

п уклонения

(111.26)

Заметил!, что

^ = X,

где л:, —результаты измерений, и —. Действительно, обо-

значив через X истинное значение измеренной величины, напишем

V. .V) *

0»-0-- -V)-—— =

(г,

Л')

- (г - Л)

2. Вычисляют приближенное зиачеиие средней квадратнческой

ошибки

г -

у Ъ <«>*

109

Я. Получают «продольное уклонение», т. е.

ёпред = З/Пд.

Уклопошш абсолютные значения которых больше 1

Г|рсд

указывают на недопустимые ошпбкп; соответствующие результаты

измерений должны быть проанализированы, а ошибки, превышающее

1пр<д. отброшены*.

Далее вычисляют по формуле (III.27) окончательное значение

пользуясь

оставшимися

после отбраковки результатами измерений.

Полученная величина т

является характеристикой случайной

ошибки одного измерения.

Что касается параметра т

, то для надежного получения его

значения требуется выполнить достаточно большое число измерений

при самых разнообразных комплексах условий и получить ряд истин-

ных ошибок. Полученные ошпбкп разбивают на группы с учетом со-

ответствующих- комплексов условий. Для каждой группы ошибок

вычисляют средние значения 8/ и рассматривают пх как конкрет-

ные значения случайпой величины б. Далее получают

| (о,Г

^о^^я • (Ш.28)

где

А* —

число групп.

Для суждения о надежности полученной характеристики влияния

систематических ошибок необходимо еще вычислить общее среднее

ср

из ошибок, т. е.

8с

Соблюдение неравенства

еср<

ТГ

(111.29)

является одним пз признаков того, что разнообразие условии учтено

достаточно хорошо.

Разумеется, надежность иараметра т

зависит и от числа групп

(желательно, чтобы К ^ 20). и от правильности учета разнообразия

условий.

Прп отсутствии истинных ошибок на группы разбивают результа-

ты измерений, руководствуясь прп этом темп же соображениями,

что и прп исследовании ряда истниных ошибок. В каждой группе

получают срсдпее я/. Эти величины х; рассматривают как конкретные

* Абсолютной велпчпве 5пред ~ Зид соответствует доверительная вероят-

воеть Р = 0,997.

110

Таблиц»

длина

хода

Ь, ь-м

22.3

33.8

14.0

42,8

29,7

35.6

9,8

43.9

19.1

10.5

20,0

22,1

21.7

46.6

14,6

34.2

25.8

16.4

29.8

27.9

20,9

21.3

14,0

Приведенная

«связна

+10,36

4-3,10

-2,14

0,00

—5,11

+11,56

-7,03

-9,50

+0,23

+19,91

+10,74

-11,70

+1.07

-8,20

—0,79

+1,02

+10,83

-5,29

+3,84

+2,46

+5,67

-2.60

-4,80

-14,85

+10,85

-13,84

+19,28

-18,80

+14,10

-15,60

+2,33

-3,68

+4,50

+3,37

-3,59

+9,54

+9,28

+7,57

-6,89

-6,87

-4,42

0,0

-19,04

—12,02

-4,29

хода

липа

холя

г.,

км

62,3

33.2

6,5

29.3

20,6

30,6

28,6

42,0

46.6

70,0

13.6

36,9

29,8

38,3

61,0

34,0

18,3

31.7

40,6

23,5

23,9

32,8

13,1

21,3

36,5

35,8

17,6

28,7

19,8

26,4

17,2

29,3

53,3

31,3

20,0

15,0

37,3

30,4

41,3

42,4

23,7

20,0

48,8

24,9

53,3

Приведенная

нсвяэкт

0 = 4=. * •

I Ь

+19,01

+0,17

—8,66

+19,40

-14,75

—8,50

+19,44

—8.95

—6,88

+1,91

-1-10,57

+6,42

+4.94

-10,18

+8,45

-1,03

—4,91

—14,39

+10,06

-0,21

-5,32

-5,24

+9,67

-4,76

+7,78

+4,01

-7,86

+0,56

+8,31

-3,89

-4,33

+9,61

—1,51

+1.61

-3,80

—1,03

—5,89

—4,30

—1,09

+14,28

-6,78

+11.41

+11,44

-15,23

-4,35

Продолжение т а б л. ад

Лг хода

Длина

ходя

I., км

Прнвслспнап

невязка

1/.

Л:

хода

Длина

хода Г„,

км

Припедепнан

нешгзка

/Л

Уь

21.3

20,2

18,7

44,7

21,0

-9,74

4-8,02

НО,69

+6,13

-11,13

100

101

102

103

104

105

106

37,9

41.1

32,9

32,5

31,5

20,7

24,0

31,0

21.2

+5,36

-3,59

+11,85

—6,32

+5,88

+15,60

+2,24

-12,75

-1,96

15,6

21,8

—12,91 1

—5.57

100

101

102

103

104

105

106

37,9

41.1

32,9

32,5

31,5

20,7

24,0

31,0

21.2

+5,36

-3,59

+11,85

—6,32

+5,88

+15,60

+2,24

-12,75

-1,96

значения некоторой случайной величины. Далее вычисляют общее

среднее х, затем уклонепня ^ = х; — х и, наконец,

V -2

Г-=1"

(11Ш

где К — число групп.

Более надежпый способ получения параметра гщ изложен в гла-

ве IV.

После определепия зпачения и т = V

\ +

1 проводят

исследование ряда в/ пли г-/ па нормальное распределение, как из-

ложено в § 22.

Пример. Даны 106 приведенных * певязок ходов нивелирования IV класса,

проложенных между реперами п марками нивелирования высших классов

(табл. 10). Выполннтьисследование ряда невязок па нормальное распределение.

Исследования:

I. Все невязкп по принципу принадлежности к второклассным полигонам

были разделены на шесть групп (I группа—с 1 по 23, II группа—с 24 по 42, III

группа—с 43 по 64, IV группа—с 65 по 81, V группа—с 82 по 95, VI группа—96 по

406). Для последующих исследований вычислены данные, помещенные

табл. 11.

II. По данным табл. 10—11 вычислены: общая средняя квадратическая

ошибка, средняя п вероятная ошибки, коэффициенты их соотношения; эксцесс,

показатель асимметрии. Результаты вычислении помещены в табл. 12.

Кроме того, вычислим т

п оцепим ее надежность

I/ 1,82 ,,

"'6= у =

0,364«*0,С мм.

Так как 8 = 0, то т^ имеет доверительные границы, обусловленные только

числом групп.

* Невязки ходов нивелирования IV класса приведены к условным невязкам

на 1 км в предположении, что их накопление происходит пропорционально корню

квадратному нз длины хода (в км).

112