Болдырев Г.Г. Методы определения механических свойств грунтов

Подождите немного. Документ загружается.

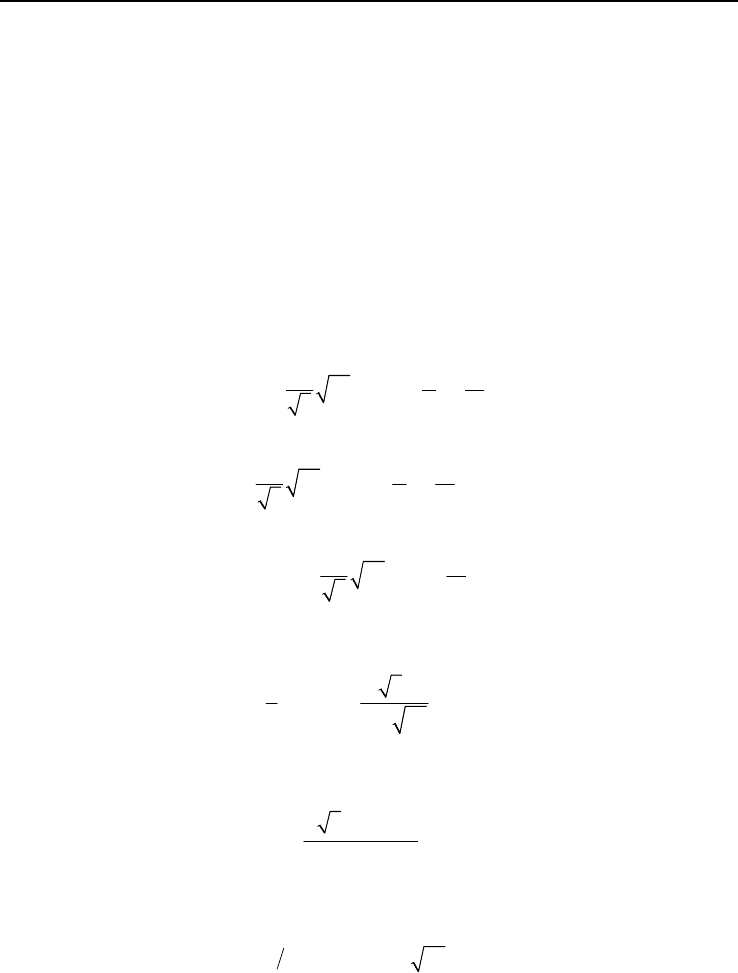
Прочность и деформируемость грунтов

2122331

I =σ σ +σ σ +σ σ

, (2.5)

3123

I =σσ σ

Тензор, у которого первый инвариант равен нулю, называется девиатором

и представляет состояние чистого сдвига. Инвариантами девиатора

напряжений являются величины:

0,J =

22 2

212 23 31

()()()/6,J

⎡

⎤

=σ−σ +σ−σ +σ−σ

⎣

⎦

(2.6)

31 2 3

()()(),J =σ−σ σ−σ σ−σ

где среднее напряжение

123

()/3σ= σ +σ +σ .

Главные напряжения выражаются через инварианты следующим образом:

cos ,

⎛⎞

σ= θ− +

⎜⎟

⎝⎠

cos ,

⎛⎞

σ= θ+ +

⎜⎟

⎝⎠

(2.7)

cos .

Jσ=− θ+

Угол

определяет направление касательного напряжения

окт

τ ,

действующего в октаэдрической плоскости (см.рис. 2.6):

arccos

⎡

⎤

θ= −

⎢

⎥

⎢

⎥

⎣

⎦

(2.8)

и изменяется от π/3 (чистое растяжение) до 0 (чистое сжатие); он связан с

главными напряжениями зависимостью

()

312

−σ−σ

θ=

σ−σ−σ

. ( 2.9)

Октаэдрические нормальное

окт

σ и касательное

окт

τ напряжения

определяются через инварианты следующим образом:

1окт

31 I=σ и

окт 2

τ=

. (2.10)

Таким образом, альтернативным вариантом инвариантам напряжений

123

,,JJJ являются напряжения

окт

σ ,

окт

τ и угол

. Очевидное преимущество

данной замены состоит в возможности физической интерпретации

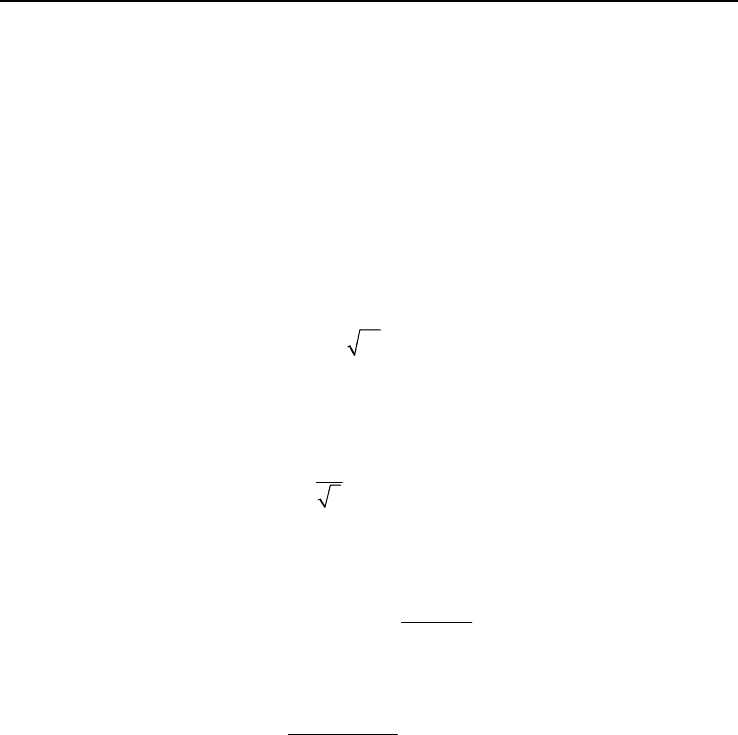
Глава 2

инвариантов напряжений. Применяя октаэдрические напряжения, мы расA

сматриваем предельное состояние грунта на плоскости, что более наглядно по

сравнению с использованием инвариантов напряжений, которые характеA

ризуют напряженное состояние в точке.

Применение октаэдрических напряжений взамен инвариантов имеет еще

одно преимущество, которое выражается в следующем. Для определения

главных напряжений необходимо решить кубическое уравнение (2.4), что

значительно сложнее, чем использование зависимостей (2.7), из которых

легко могут быть найдены главные напряжения.

В некоторых случаях удобнее использовать не второй инвариант

девиатора напряжений, а интенсивность касательных напряжений, которая

выражается следующим образом:

σ=

. (2.11)

В частном случае при испытании образцов грунта в стабилометре в

условиях осесимметричной деформации, когда

σ=σ, интенсивность

касательных напряжений находится из выражения

()

σ= σ−σ

. (2.12)

Schofield (1968) предложил использовать при обработке результатов

трехосных испытаний (осесимметричная деформация) два других инварианта

напряжений:

q =σ −σ и

σ+ σ

= . (2.13)

Для характеристики напряженного состояния часто вводится параметр

Лоде

213

σ−σ−σ

μ=

σ−σ

. (2.14)

Параметр Лоде

используется для определения вида напряженного

состояния следующим образом. Для случая одноосного сжатия

123

(0, 0)σ> σ=σ= и при нагружении образца грунта в стабилометре по

траектории стандартного трехосного сжатия, когда

123

σ>σ=σ, из выражения

(2.11) получаем:

=− ;

3θ=π . В случае одноосного растяжения

12 3

(0,0)σ=σ= σ<

или при испытании в приборе истинного трехосного

сжатия по траектории, когда

123

σ=σ>σ, параметр Лоде 1

=+ ;

0θ=

. В

условиях чистого сдвига, когда

σ=−σ, а

0σ= , значения 0

= ; /6θ=π .

Таким образом, параметры

изменяются в следующих пределах:

11,/30

−≤

≤+ π ≥θ≥

. (2.15)

Прочность и деформируемость грунтов

Вид напряженного состояния оказывает влияние на параметры прочности

в большей степени, чем на параметры деформируемости. Испытания в

стабилометре проводятся только при одном виде напряженного состояния,

когда

=−

, но могут быть выполнены по различным траекториям

нагружения. В приборе истинного трехосного сжатия можно провести

испытания при значениях параметра Лоде

=− , 1

=+ , 0

= .

2.3. Геометрическое представление напряженного состояния

и инвариантов

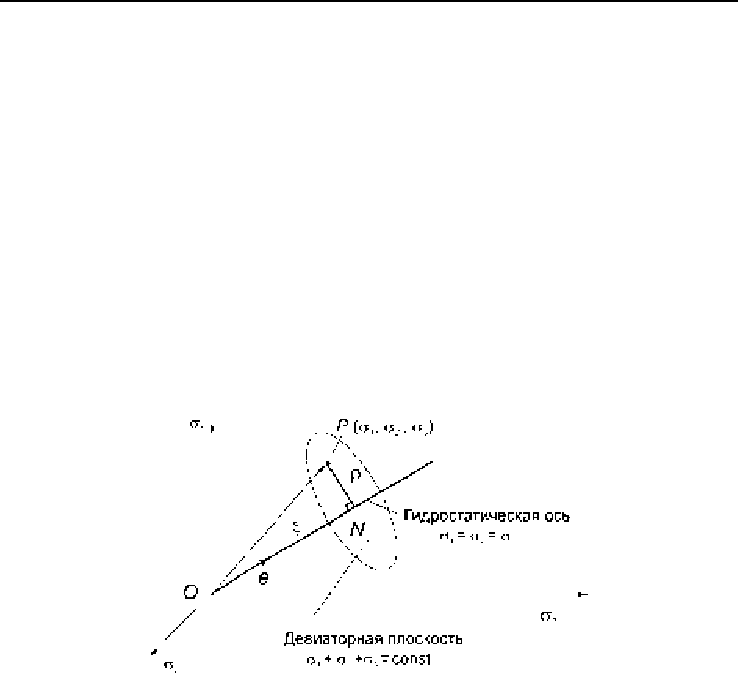
Напряженное состояние в какойAлибо точке Р

123

(, , )σσσ

может быть

представлено геометрически в пространстве главных напряжений соотA

ветствующими значениями их координат (рис. 2.5). Поэтому векторы ОN и

NР нагляднее представляют напряженное состояние, чем сама точка Р.

Рис. 2.5. Геометрическое представление напряженного состояния

в пространстве главных напряжений

Два любых напряженных состояния на точке Р, которые различаются

положением их главных осей, но не по величине главных напряжений, могут

быть представлены одной и той же точкой. Это обстоятельство свидеA

тельствует о том, что в подобном пространстве напряжений главным является

геометрия напряженного состояния, а не его ориентация по отношению к

материальному элементу. Для изотропных материалов условие прочности

должно быть инвариантной функцией напряженного состояния, и это усA

ловие может быть представлено как поверхность в пространстве напряжений.

На рис. 2.5 прямая линия ОN, которая равнонаклонена по отношению к

трем координатным осям, называется гидростатической осью. Каждая точка

на этой оси соответствует гидростатическому напряженному состоянию

= σ

. Единичный вектор е вдоль этой оси определяется как

Глава 2

е = (1/3)(1, 1, 1). Плоскости, перпендикулярные к гидростатической оси,

называются девиаторными плоскостями, а девиаторная плоскость

123

0σ+σ+σ = , которая проходит через точку О начала пространства главных

напряжений, называется

π Aплоскостью. Любая точка напряжений на π A

плоскости представляет состояние чистого сдвига.

Напряженное состояние, соответствующее вектору ОР на рис. 2.5, может

быть разложено на две компоненты. Первая компонента ОN вдоль

гидростатической оси и вторая компонента NP в девиаторной плоскости

перпендикулярно гидростатической оси. Длины

векторов ON и NP,

соответственно, определяются

1/ 3I

окт

σ ,

окт

τ . (2.16)

Таким образом,

определяют гидростатическую и девиаторную

часть, соответственно, напряженного состояния, представленного вектоA

ром ОР.

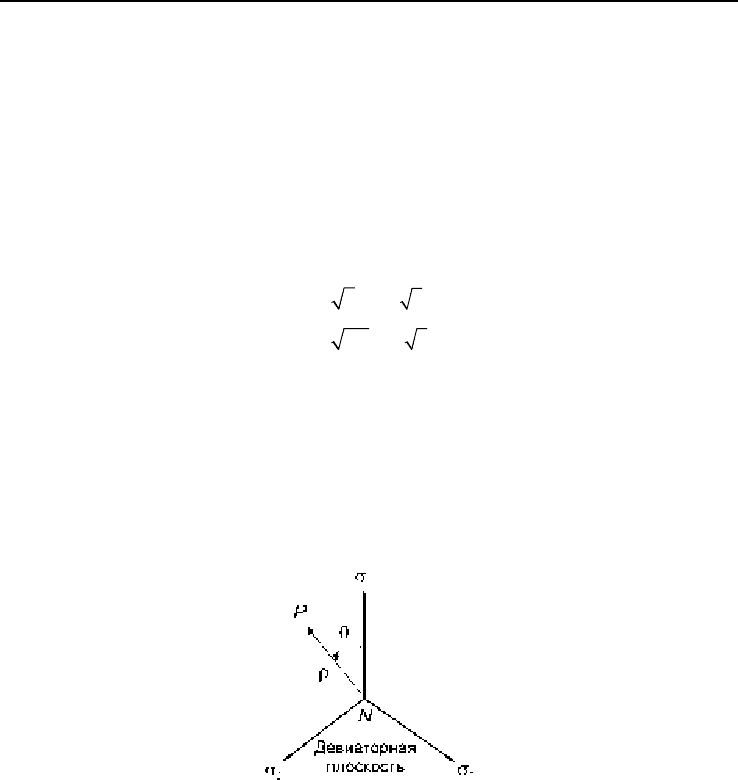
На рис. 2.6 координатные оси σ

, σ

перенесены на девиаторную

плоскость. Угол

на этом рисунке измеряется от положительного

направления оси

к вектору NP. Этот угол определяется из выражения (2.9)

и изменяется в интервале от 0 до 60°.

Рис. 2.6. Представление напряженного состояния и координатных осей σ

, σ

в девиаторной плоскости

Основываясь на различных приведенных соотношениях поверхность

прочности

123

(, , )0f σσσ = или

123

(, , ) 0fI I I = можно представить геометA

рически через

(см.рис. 2.4, 2.5) или через

окт

σ ,

окт

τ и

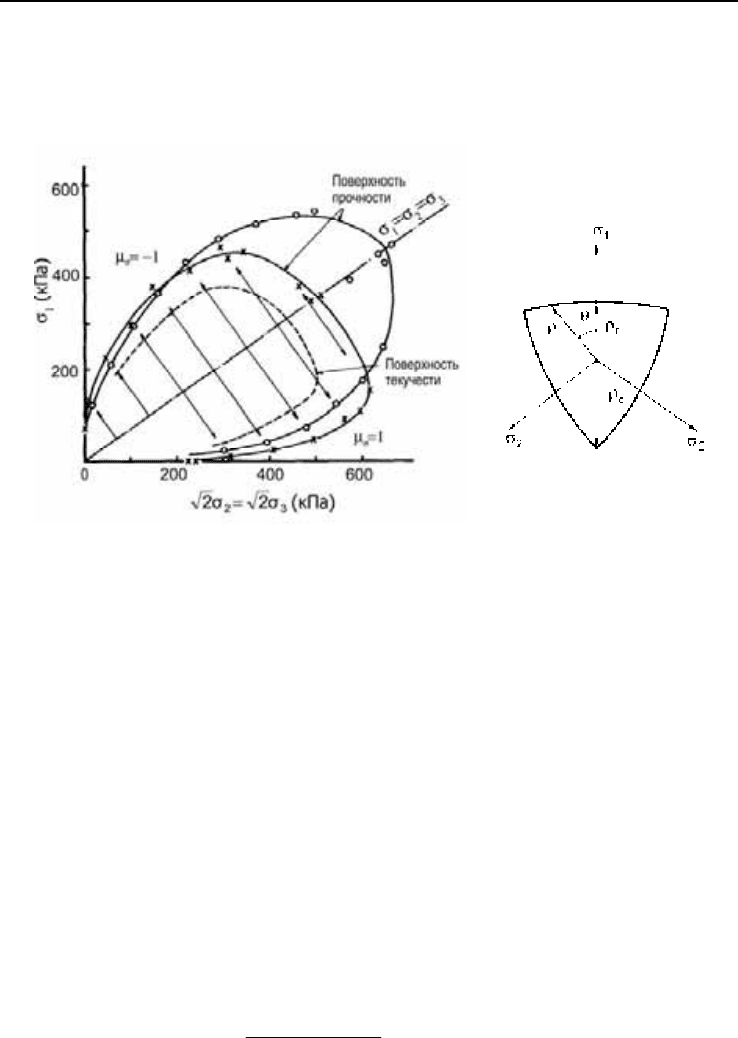
Общую форму поверхности прочности в пространстве главных напряA

жений лучше представить с помощью двух сечений: меридианной плоскостью

(рис.2.7, а) и девиаторной плоскостью (рис. 2.7, б). Сечение девиаторной

плоскостью при произвольном значении инварианта

const

показывает

Прочность и деформируемость грунтов

поперечную форму поверхности разрушения или ее след в девиаторной

плоскости. Сечение меридианной плоскостью при

= const показывает

очертание поверхности между осью гидростатического давления и преA

дельной огибающей.

(а) (б)

Рис. 2.7. Форма поверхности прочности в меридианной (а)

и девиаторной (б) плоскостях

Вследствие того что поверхность прочности, как правило, симметрична

относительно гидростатической оси, в опытах ограничиваются исслеA

дованиями в секторе 0 <

< 60°. В общем случае, в особенности для сыпучих

сред, поверхность прочности несимметрична относительно оси гидростатиA

ческого давления. Меридиан сжатия

оказывается больше меридиана расA

ширения

, что показано на рис. 2.7, б. Значения прочности, полученные из

опытов, выполненных по траектории сжатия, отличаются от значений

прочности, полученных из испытаний по траектории расширения.

2.4. Условия прочности в инвариантах напряжений

Наиболее простым из известных является условие прочности, сфорA

мулированное в 1773 г. Ш. Кулоном, которое, с использованием представления

напряженного состояния Мора (рис. 2.8,б), можно записать в виде

sin

2ctg

σ−σ

σ+σ+ ϕ

. (2.17)

Глава 2

Из выражения (2.17) видно, что величина промежуточного главного напряжеA

ния

не входит в это выражение и, следовательно, не влияет на прочность

грунта.

С использованием этого условия прочности разработаны теория преA

дельноAнапряженного состояния сыпучей и связной среды и ее приложение к

решению ряда инженерных задач.

В инвариантах напряжений

,IJ и

условие прочности (2.17) может

быть представлено в виде

12 1

3(1 sin )sin 3(3 sin )cos

(, ,) sin

3cos 0;

fI J I

⎛⎞

θ+ −

θ=−

+×

⎜⎟

⎝⎠

×− ϕ=

(2.18)

3(1 sin )sin 3(3 sin )cos

(,,) 6 sin

32cos 0.

⎛⎞

θ+ −

ξρ

θ=−

ξϕ

+×

⎜⎟

⎝⎠

×ρ − ϕ =

(2.19)

В пространстве главных напряжений условие прочности Мора – Кулона

представляет неправильную гексагональную пирамиду, как показано на

рис. 2.8, 2.9.

Рис. 2.8. Условие прочности Мора – Кулона:

а – в пространстве главных напряжений; б – в меридианной плоскости

Прочность и деформируемость грунтов

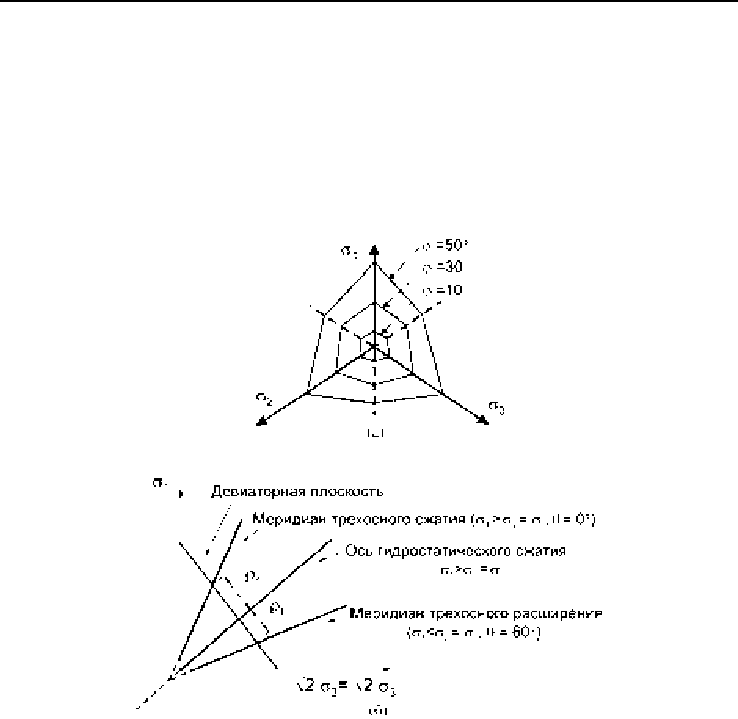
На рис. 2.9, а показано семейство поперечных сечений поверхности

прочности Мора – Кулона для различных значений

. На рис. 2.9, б приA

ведены огибающие поверхности прочности при сжатии и расширении

(

сжатие θ = 0° и расширение θ = 60°). Трехосное напряженное состояние

вдоль траекторий трехосного сжатия (ТС) (σ

) и трехосного

расширения (ТЕ) (σ

) приводит к разрушению на меридианах сжатия

и расширения, соответственно.

Рис. 2.9. Семейство сечений поверхностей прочности Мора – Кулона

в девиаторной (а) и меридианной (б) плоскостях

Условие прочности Мора – Кулона не отражает реального поведения

грунтов. ВоAпервых, в него не входит промежуточное главное напряжение

σ ,

и, следовательно, оно не влияет на прочность грунтов, что противоречит

результатам опытов с образцами грунтов. ВоAвторых, очертание огибающей

поверхности прочности в меридианной плоскости не является прямой, а

имеет кривизну, которая зависит от гидростатического давления. Это

подтверждается рядом исследований, выполненных различными авторами.

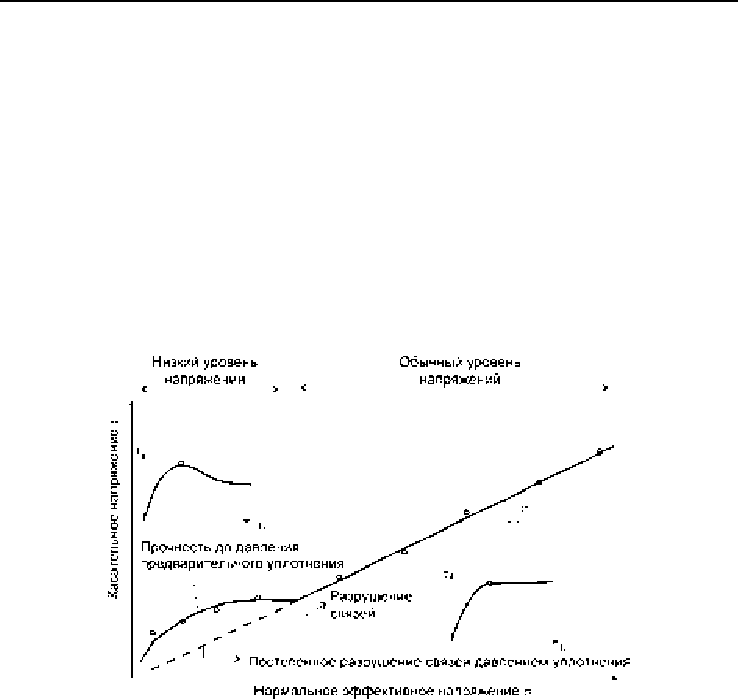
На рис. 2.10 показаны типичные характеристики прочности элювиальных

грунтов (Chin and Sew, 2001) при низком уровне напряжений (менее 50 кПа) и

обычных грунтов при определении прочности в лабораторных условиях, т.е. при

Глава 2

нормальных давлениях (100–300 кПа). Зависимость

()fτ= σ

построена с исA

пользованием касательного напряжения, соответствующего пику прочности

max

τ=τ

. При низком уровне нормальных напряжений (обычно не более

кПа) элювиальные грунты сопротивляются сдвигу преимущественно

структурными связями. С ростом нормального давления структурные связи

разрушаются, и элювиальные грунты ведут себя подобно нормально

уплотненным или слегка переуплотненным аллювиальным грунтам. ПредельA

ное состояние характеризуется углом внутреннего трения

. На рис. 2.10 в

области низких нормальных давлений поверхность прочности имеет криволиA

нейное выпуклое очертание, а в области больших давлений она практически

прямолинейна. Известно, что в опытах при нормальных давлениях порядка

600–1000

кПа прочность грунта уменьшается с ростом давления.

Рис. 2.10. Эффект влияния нормального давления на прочность в условиях

дренированного сдвига (Chin and Sew, 2001)

Подобное влияние всестороннее давление оказывает и на прочность

песчаных грунтов (Stroud, 1971).

Поэтому в грунтах, особенно при небольших значениях среднего наA

пряжения, угол внутреннего трения зависит от его величины. Это условие

особенно неудобно при численном решении трехмерных задач, так как

наличие углов на поверхности (отсутствие гладкости) усложняет решение.

Эта особенность учтена в модели грунта № 147 программы LSADYNA (Lewis,

2004).

Несмотря на это, условие прочности Мора – Кулона широко

применяется на практике, главным образом изAза его простоты и приемлемой

точности при решении большинства инженерных задач в области геотехники.

Прочность и деформируемость грунтов

В 1952 году Drucker and Prager (Друкер – Прагер) предложили условие

прочности (рис. 2.11), полученное с использованием условия Мизеса, но с

учитетом влияния среднего напряжения на прочность грунтов

12 2 1

(, ) 0,fI J J I k=−α−=

(2.20)

где

и α – параметры, определяемые экспериментально. Эти параметры

связаны с параметрами прочности Мора – Кулона

()

ϕ±

=α

sin33

sin2

6cos

3(3 sin )

± ϕ

. (2.21)

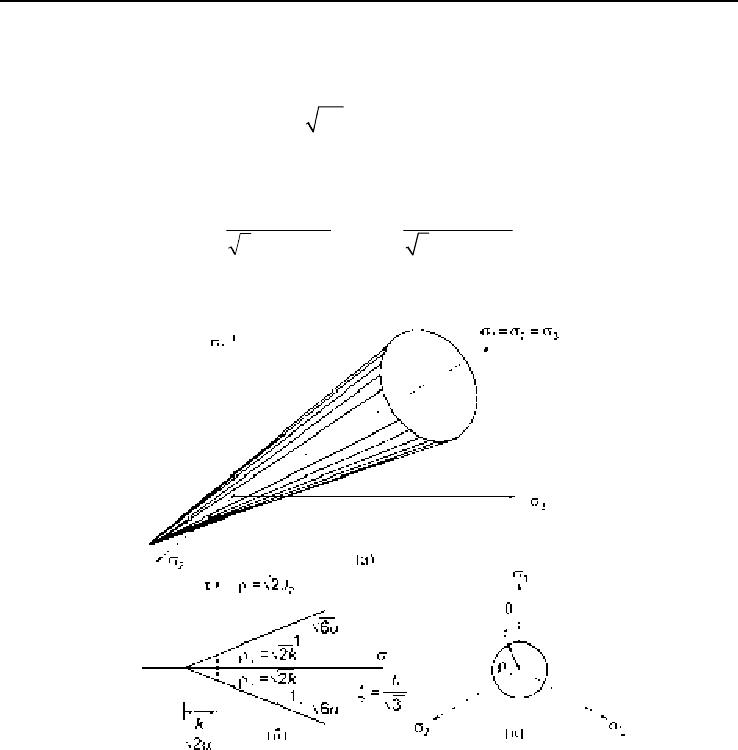
Рис. 2.11. Условие прочности Друкера – Прагера:

а – пространство главных напряжений; б – меридианная плоскость (

= const);

в – девиаторная плоскость

В выражениях (2.21) знак «–» вводится в случае приведения условия

прочности Друкера – Прагера к условию прочности Мора – Кулона при

испытаниях по траектории сжатия, т.е. когда

= 0°, и знак «+» вводится,

когда сопоставляются результаты испытаний по траектории расширения при

= 60°.

Поверхность прочности в пространстве главных напряжений показана на

рис. 2.11, а. Эта поверхность является правильным круговым конусом с

пространственной диагональю, на которой выполняется условие

123

σ=σ=σ

След этой поверхности в меридианной плоскости (

= const) и девиаторной

Глава 2

плоскости показан на рис. 2.11, б, в, соответственно. Это условие более

удобно при численном решении, так как имеет гладкую поверхность. Как

видно из рис. 2.12, поверхность прочности Мора – Кулона находится между

двумя поверхностями Друкера – Прагера, которые построены по значениям

, найденным из опытов по траекториям нагружения ТС и ТЕ, соотA

ветственно. Поэтому, если использовать условие прочности Друкера –

Прагера, то при определении параметров

необходимо точно знать,

какое напряженное состояние возникает в основании, так как

зависят

от его вида (см. рис. 2.2).

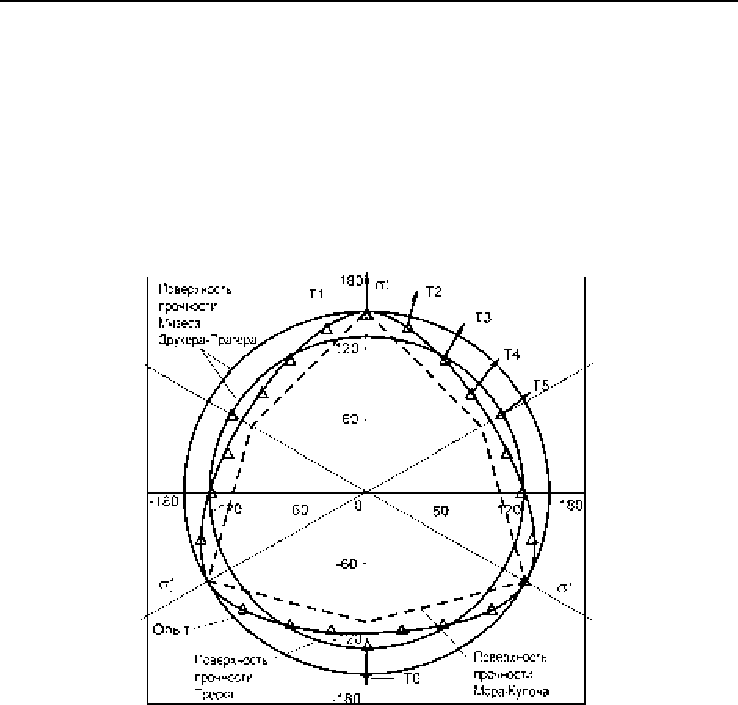
Рис. 2.12. След поверхностей прочности в девиаторной плоскости (Prashant, 2005)

Более подробную информацию о других условиях прочности можно найти

в работах В.Г. Федоровского (1985), Das (1997), MaoAhong Yu (2002).

2.5. Траектории напряжений и их влияние на механические

свойства грунтов

При описании поведения грунтов с использованием математического

аппарата теории пластичности принято различать нагружение и разгрузку.

Нагружением называется процесс, при котором происходит нарастание пласA

тических деформаций, а процесс, сопровождающийся уменьшением упругой