Бобцов А.А., Лямин А.В., Чежин М.С. Операторный метод анализа и синтеза линейных систем управления
Подождите немного. Документ загружается.


Тогда допустима передаточная функция (2.41), если исходные требования удовле-
творяют дополнительному условию
2
2
10
fy
y
f
ωδ
ω
≥δ . (2.44)
В противном случае, но при условии
3
1
T
f
µ>ω ,
3
1
µ
>δ
f
(2.45)
можно использовать функцию вида
)1)(1)(1(
)1(
)(
431
2
+++
+
=
∗
sTsTsTs
sTk
sW
p
p
, (2.46)
с теме же параметрами, но при
34
1
TT
µ
=
. (2.47)
Все записанные выше формулы вытекают из вида асимптотических ЛАХ,
представленных на рис.2.5.
Когда найдена желаемая передаточная функция разомкнутой системы
, то
для того, чтобы обеспечить выполнение тождества (2.16) необходимо положить
)(
sW
p
∗
)()()(
1
2
sWsWsW
py
∗−
= . (2.48)
На этом этапе проверяется
условие строгой реализуемости передаточной функции
регулятора. Последнее означает, что степень числителя не должна превышать сте-
пени знаменателя. Если степень числителя передаточной функции
выше сте-
пени знаменателя, то можно воспользоваться законом
)(
2
sW
∏
+
=
∗−
ε
i
i
p
sT
sWsWsW
)1(
1
)()()(
1
,
c
i
T
ω>>
1
. (2.49)
После определения передаточной функции регулятора следует найти характери-
стический полином замкнутой системы (2.18) и по его корням оценить устойчивость
системы. Рассчитать передаточную функцию разомкнутой системы
и определить запас устойчивости по амплитуде и фазе. Запасом
)()()(
2
sWsWsW
yp
=
21
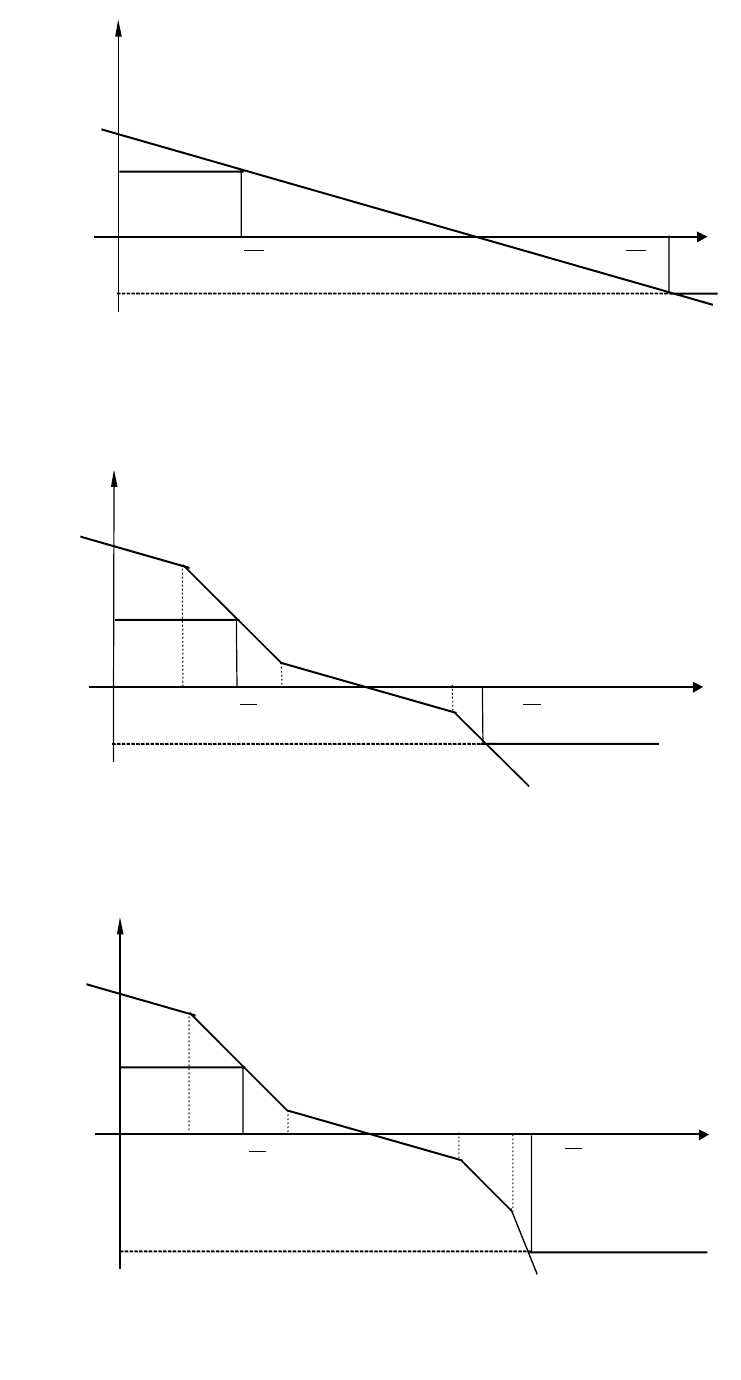
f
ωlg
-20 дБ/дек
1
lg
δ
−
f
δlg20
y
δ− lg20
y
ωlg
а) ЛАХ передаточной функции (2.40)
ωlg
)(ω
p
L
f
ω
lg
c
ω
-20 дБ/дек
f
δlg20
y
δ− lg20
y
ωlg
b) ЛАХ передаточной функции (2.41)
ωlg
)(ω
p
L
1/
T
1
1/
T
2
1/
T
3
f
ω
lg
c
ω
-20 дБ/дек
f
δlg20
y
δ− lg20
y
ωlg
c) ЛАХ передаточной функции (2.46)
ωlg
)(ω
p
L
1/
T
1
1/
T
2
1/
T
3
1/
T
4
Рис. 2.5. ЛАХ допустимых передаточных функций
2
2
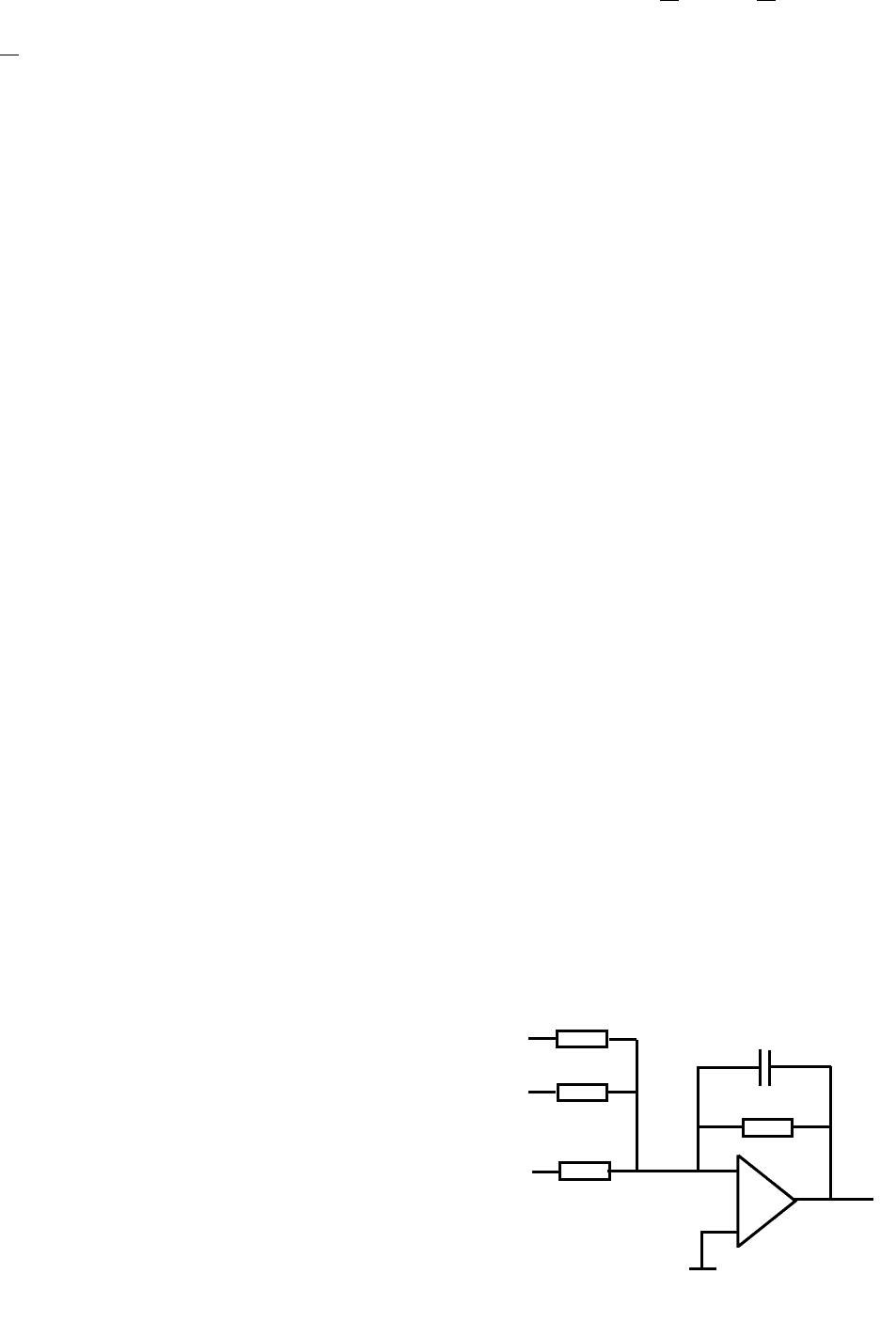
устойчивости по амплитуде называется величина
)(
ω
−
=
∆
p
LL , где ω таково, что
π−=ωϕ )(
p
. Величина )(
cp
ω
ϕ+π=ϕ∆ называется запасом устойчивости по фазе.
Для удовлетворительной работы системы необходимо выполнение условий
дБ6≥∆
L
, . (2.50)
0
30≥ϕ∆
Если последние требования не выполнены, то следует видоизменить желаемую ЛАХ
разомкнутой системы и заново определить передаточную функцию
W . )(
2
p
В заключении раздела строится ЛАХ и ЛФХ передаточной функции разомкнутой
системы W
.
)(s
p
2.4. Построение электронной модели регулятора
Построение электронной модели регулятора включает три этапа. На первом этапе
осуществляется преобразование модели вход – выход регулятора
)
~
)()()((
210
ε
+
−
= pWypWpWu
к модели вход-состояние-выход
ε
+
+=
~
21
ByBAxx
&
,
ε
+
+
=
~
21
DyDCxu , (2.51)
где матрицы
такие, что
2121
,,,,, DDCBBA
11
1
10
)()()( DBAIpCpWpW +−=−
−
,
22
1
20
)()()( DBAIpCpWpW +−=
−
,
а также построение по уравнениям (2.51) структурной схемы на элементарных
звеньях: сумматор, интегратор, усилитель. На
следующем этапе в построенной структурной
схеме сумматоры, интеграторы и усилители
заменяются на блоки состоящие из операци-
онного усилителя, резисторов и конденсато-
ров, электрическая схема которого представ-
лена на рис. 6. Данный блок осуществляет
преобразование сигналов
в сиг-
k
zzz ,,,
21
K
1
z
2
z
k
z
1
R
2
R
k
R
C
R
z
Рис. 2.6. Электронный блок
23

нал
по формуле z
∑
=
−=
+
k
i
i
i
z
R
zCp
R
1
11
. (2.52)
На последнем этапе, составляются уравнения электронной модели регулятора и
находятся значения сопротивлений резисторов и емкости конденсаторов включен-
ных в схему.
После построения электронной модели необходимо скорректировать значения ко-
эффициентов передаточных функций регуляторов в соответствии с существующими
номинальными значениями параметров электронных элементов, использованных
при построении электронной модели.
2.5. Исследование замкнутой системы управления
Исследование замкнутой системы управления производится по структурной схе-
ме на рис. 2.3 и включает проведение следующих вычислительных экспериментов:
1) построение процесса
при ; yt() yt tft
∗
==() (), ()10
2) построение процессов
ε при )(),( tyt
∗
yt atft
∗
==() , ()
1
0 ;
3) построение процессов
ε при )(),( tyt
∗
yt a tft
yy
∗
==() cos( ), ()ω 0 ;
4) построение процессов при ε(), ()tft yt ft a t
ff
∗
==() , () cos( )0 ω ;
5) построение процессов
при )(),(),( tftyty
∗
yt a tft a t
yy f
∗
==() cos( ), () cos( )ωω
f
.
По результатом экспериментов требуется определить время переходного процесса,
перерегулирование, а также максимальные по модулю значения установившейся
ошибки в каждом эксперименте.
24
3. ПРИМЕР РАСЧЕТА СИСТЕМЫ УПРАВЛЕНИЯ
3.1. Постановка задачи управления
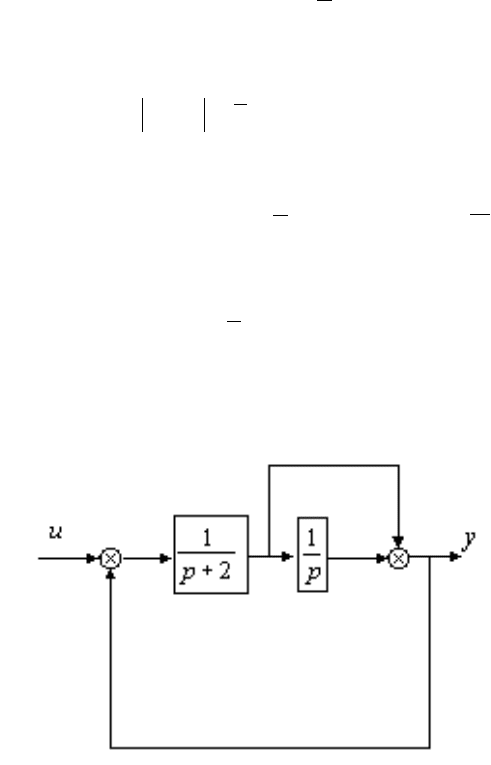
Рассмотрим процедуру синтеза регулятора для объекта управления, структурная
схема которого представлена на рис. 3.1. Будем считать, что следящая система
должна удовлетворять следующим требованиям:
1) запас устойчивости по амплитуде не менее 6 дБ, а запас устойчивости по фазе
не менее 30
0
;
2) установившаяся ошибка )
отработки сигнала
(t
∞
ε
5.0||,*
1110
=
≤
+
= aataay (3.1)
должна удовлетворять условию
05.0)(
1
=
ε
≤
ε
∞
t ; (3.2)
3) установившаяся ошибка )
ε отработки сигнала
(t
∞
=
ω
≤
ω
=
≤
ω
=
yyyyyy
aatay ||,25.0||),cos(* 1 (3.3)
должна удовлетворять условию
05.0|)(|
=
ε
≤
ε
∞ y
t ; (3.4)
Рис. 3.1. Структурная схема объекта управления
25

4) установившаяся ошибка )
, вызванная наличием помехи
(t
∞
ε
500||,1.0||),cos(
=
ω
≥
ω
=
≤
ω=
ffffff
aataf (3.5)
должна удовлетворять условию
01.0|)(|
=
ε
≤
ε
∞ f
t . (3.6)
3.2. Анализ объекта управления
По структурной схеме определим передаточную функцию. Введем дополнитель-
ные переменные как показано на рис. 3.2 и представим переменную )(
t
y относи-
тельно входа )(
t
u :
=
+
=+=+=
22221
11
x
p
p
xx
p
xxy
)(
2
11
yu
pp
p
+
+
+
. (3.7)
Рис. 3.2. Структурная схема объекта управления
Откуда следует
upyppp )1()12(
2
+=−−+ (3.8)
и передаточная функция имеет вид
1
1
)(
2
−
+
+
=
s
s
s
sW . (3.9)
Характеристический полином системы 01
2
=
−
+
s
s
имеет корни с положительной
вещественной частью и, следовательно, объект управления неустойчив. Корень чис-
26

лителя является нулем передаточной функции и равен -1. Таким образом, данная пе-
редаточная функция является минимально-фазовой и решение задачи управления
существует.
Логарифмическая амплитудная частотная характеристики (ЛАХ) и логарифмиче-
ская фазовая частотная характеристики (ЛФХ) представлены на рис. 3.3.
3.3. Решение задачи стабилизации
Представим сигнал управления в виде
))((
210
uupWu
+
= , (3.10)
где
)(
)(
)(
0
0
0
pa
pb
p =W - дробно – рациональная функция.
Рис. 3.3. ЛАХ и ЛФХ объекта управления
Определим алгоритм формирования переменной для того, чтобы решить задачу
стабилизации. Для этого выберем алгоритм формирования сигнала
в виде
1
u
1
u
ypWu )(
11
−
=
, (3.11)
27

где
)(
)(
)(
1
1
1
pa
pb
p =W . Подставляя (3.9), (3.11) в уравнение (2.2) и разрешая его относи-
тельно выходной переменной, найдем уравнение замкнутой системы
2
)( upWy
y
=
,
где
)()()()()()1(
)()()1(
)()()(1
)()(
)(
1010
2
10
10
0
pbpbpbpapapp
papbp
pWpWpW
pWpW
pW
y
+−+
+
=
+
= . (3.12)
Рассчитаем полиномы
из условия
)(),(),(),(
1010
pbpbpapa
)(
1
)()()()()()(
)()()(
1010
10
papbpbpbpapapa
papbpb
y
=
+
, (3.13)
где )a
- произвольный устойчивый полином степени
( p
y
112 =−
=
−
mn .
Пусть полином 1)( +
=
ppa
y
, тогда
1)1()()(
1
01
+=+==
−
pppbpa
n
(3.14)
и, используя следующее тождество
12
10
)1)(()()()()(
−−
+=+
mn
ppbpbpbpapa , (3.15)
найдем коэффициенты многочленов
.
)(),(
10
pbpa
Тогда, подставляя соответствующие числовые значения в уравнение (3.15), получа-
ем
))(1())(1(
0,11,10,01,0
2
bpbpapapp ++++−+
2
)1( += p )1( +
p
. (3.16)
Откуда следует
=−+++−++++ )()()(
0,00,11,10,11,00,0
2
1,11,00,0
3
1,0
abpbbaapbaapa
133
23
+++= ppp . (3.17)
Приравнивая члены при соответствующих степенях, получаем
1
1,0
=
a ,
3
1,11,00,0
=
+
+
baa ,
3
1,10,11,00,0
=
+
+
−
bbaa ,
1
0,00,1
=
−
ab ,
28

откуда следует
2
1,10,0
=
+
ba ,
4
0,01,10,1
=
+
+
abb ,
0,00,1
1 ab
+
=
.
Производя простые преобразования, находим коэффициенты полиномов
и
. В нашем случае получилось:
)(
0
pa
)(
1
pb 1
0,01,0
=
=
aa и 1
1,1
=
b , . Таким образом
передаточные функции регуляторов имеют вид:
2
0,1
=b
1
1
0
+
+
=
s
s
W и
1
2
)(
1
+
+
=
s
s
sW ,
а передаточная функция замкнутой системы:
1
1
)(
+
=
s
sW
y
.
ЛАХ и ЛФХ замкнутой системы представлены на рис. 3.4. Структурная схема сис-
темы управления приведена на рис. 3.5. Результаты компьютерного моделирования
представлены на рис. 3.6 иллюстрируют асимптотическую устойчивость системы.
При постановке эксперимента были выбраны ненулевые начальные условия на ин-
теграторе с выходом .
1
x
3.4. Расчет передаточной функции регулятора
Управляющее воздействие объектом (3.13) строится в форме:
ε
=
~
)(
2
pWu , (3.18)
где
)(
)(
)(
2
2
2
pa
pb
p =W .
Для расчета передаточной функции регулятора воспользуемся методом, предпо-
лагающим построение желаемой передаточной функции замкнутой системы, удов-
летворяющей выше перечисленным требованиям и синтез регулятора на соответст-
вии между логарифмическими частотными характеристиками.
29
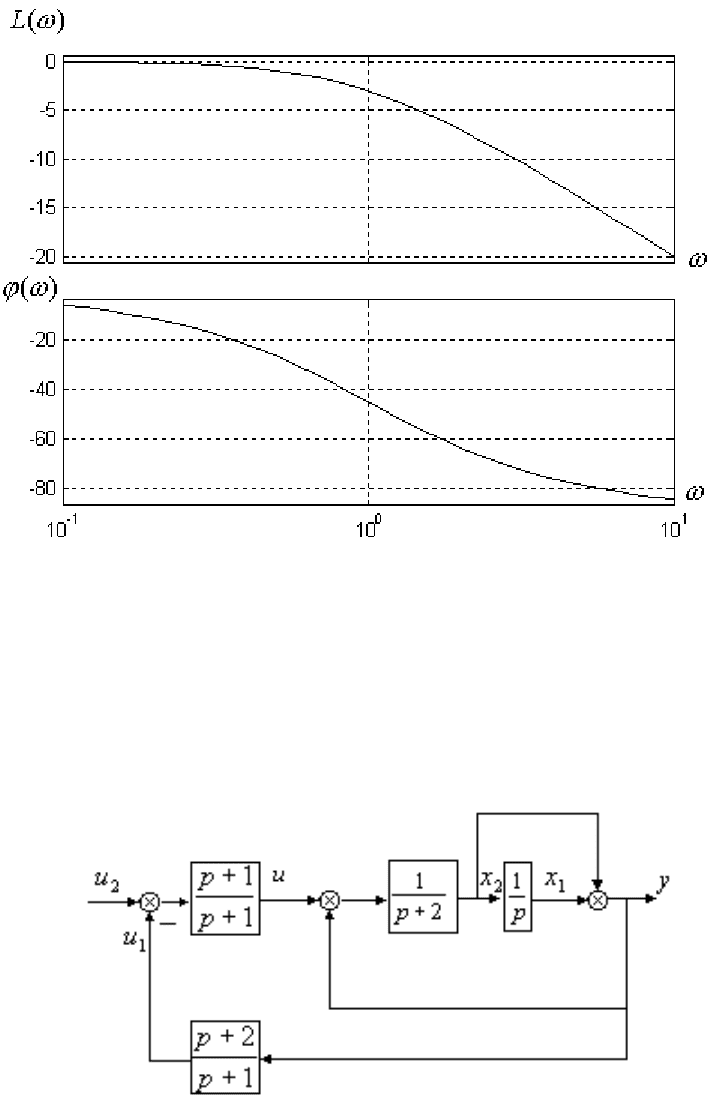
Рис. 3.4. ЛАХ и ЛФХ замкнутой системы
Рис. 3.5. Структурная схема системы управления
30
