Бобцов А.А., Лямин А.В., Чежин М.С. Операторный метод анализа и синтеза линейных систем управления

Подождите немного. Документ загружается.

)]([)(

к изображению входной переменной

)]([)(

при нулевых начальных условиях

)0()0()0()0()0()0(

yppuuyppyy

mn −−

======= KK .

Напомним, что преобразование Лапласа

∫

∞

−

)()]([)( dtetftfLsF

ставит в соответствие каждой функции )(

(оригиналу), для которой несобствен-

ный интеграл сходится, единственную функцию )(

F (изображение) комплексной

переменной

. Использование преобразования Лапласа для изучения дифференци-

альных уравнений основывается на утверждении:

)()]([ sFstfpL

= ,

если равны нулю значения )(

и ее производных вплоть до ( )–ой при 1−k 0

Применяя преобразование Лапласа к правой и левой частям уравнения (2.1) при

нулевых начальных условиях, получим

)()()()(

и, следовательно, передаточная функция -

)(

sW = . (2.3)

Передаточная функция у которой полиномы )(

a и )(

b не являются взаимно

простыми называется вырожденной передаточной функцией. При выводе переда-

точной функции )(

W системы необходимо следить за тем, чтобы не произошло со-

кращения ее числителя и знаменателя. При выполнении последнего условия, знаме-

натель )(

a передаточной функции называется характеристическим полиномом

системы. Устойчивость объекта управления определяется корнями характеристиче-

ского уравнения 0)(

a . Для асимптотической устойчивости необходимо и доста-

точно отрицательность вещественных частей всех корней. Любой полином, все кор-

ни которого имеют строго отрицательную вещественную часть, называется устой-

чивым полиномом.

Корни знаменателя передаточной функции называются полюсами, а корни числи-

теля - нулями. Передаточная функция, у которой вещественные части всех нулей от-

рицательны называется минимально-фазовой. Для существования решения задачи

управления достаточно, чтобы передаточная функция была минимально-фазовой.

Если )(

W не является минимально-фазовой передаточной функцией, то решение

задачи управления может существовать только при условии, что наибольшее общее

кратное полиномов )(

a и )(

b - устойчивый полином.

Если )(

W является минимально-фазовой передаточной функцией, то решение

задачи будем искать в два этапа. Для этого представим сигнал управления в виде

))((

210

uupWu

= , (2.4)

где

)(

pW = - дробно – рациональная функция. На первом этапе определим

алгоритм формирования переменной для того, чтобы решить задачу стабилиза-

ции, т.е. обеспечить выполнение предельного соотношения

при любых

начальных условиях. На втором этапе, выбором сигнала управления обеспечим ре-

шение задачи слежения, т.е. выполнение неравенства

, где -

функция времени такая, что

0)(lim =

∞→

γ≤−

∗

|)() ty

∞

(| ty )(ty

∞

0)]()([lim

−

∞

∞→

tyty

)(ty

∗

- заранее неизвестная переменная величина (задающее воздействие), а 0>

некоторое заданное постоянное число. Отметим, что определенная подобным обра-

зом функция )

называется установившейся реакцией системы.

(ty

∞

В заключении первого этапа курсовой работы строятся ЛАХ и ЛФХ передаточной

функции )(

W объекта управления. Напомним, что логарифмической амплитудно-

частотной характеристикой, соответствующей передаточной функции )(

W , назы-

вается график функции

|)(|lg20)(

ω jW

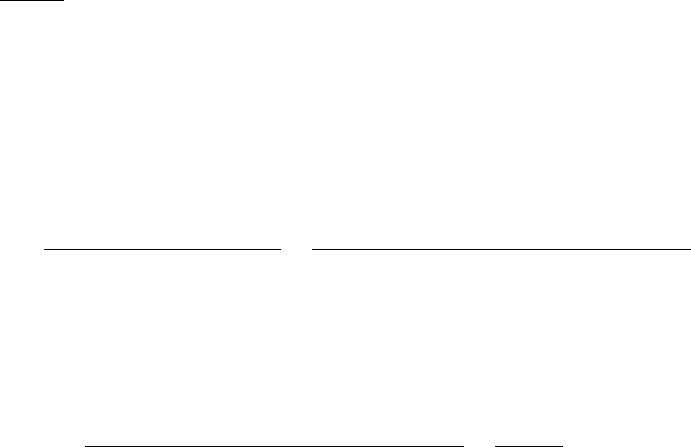
от логарифма , где - действительная переменная, которая называется часто-

той. Функция ), которую получают из передаточной функции )

ωlg

( jW

ω (

W при под-

становке в нее

ωj=

, называется частотной передаточной функцией. Принято

измерять значение ЛАХ в

децибелах (дБ), а значение наклона ЛАХ – в децибелах на

декаду

. Декадой называют интервал на котором частота

меняется в 10 раз. Лога-

рифмической фазочастотной характеристикой называется график функции

)(arg)(

ωϕ jW

от логарифма

lg . ω

2.2. Решение задачи стабилизации

Для решения задачи стабилизации выберем алгоритм формирования сигнала

виде

ypWu )(

−

, (2.5)

где

)(

p =W

. Подставляя (2.4), (2.5) в уравнение (2.2) и разрешая его относи-

тельно выходной переменной найдем уравнение замкнутой системы

)( upWy

, (2.6)

где

)()()()()()(

)()()(

)()()(1

)()(

)(

1010

pbpbpbpapapa

papbpb

pWpWpW

pWpW

= . (2.7)

Для объектов управления с минимально-фазовыми передаточными функциями, по-

линомы )

выбирают из условия

(),(),(),(

1010

pbpbpapa

)(

)()()()()()(

)()()(

1010

papbpbpbpapapa

papbpb

, (2.8)

где )

- произвольный устойчивый полином степени

(

−

. Например, полином

можно выбрать следующим образом

)

(

ppa

−

+= )1()( , (2.9)

а многочлены

)(),(),(),(

1010

pbpbpapa

0,0

2,0

1,00

)( apapapa

+++=

−

K ,

0,1

2,1

1,11

)( apapapa

+++=

−

K ,

0,0

2,0

1,00

)( bpbpbpb

+++=

−

K ,

0,1

2,1

1,11

)( bpbpbpb

+++=

−

K ,

где )4

неизвестных коэффициентов этих полиномов находятся из тождеств

−n

)1()()(

−

+==

ppbpa , (2.10)

)1)(()()()()(

−−

+=+

ppbpbpbpapa . (2.11)

Таким образом, принимая во внимание

(2.7), (2.9)-(2.11), передаточная функ-

ция объекта управления охваченного

отрицательной обратной связью по вы-

ходу будет иметь вид

⊗

)( pW

)(

Рис. 2.2. Структурная схема

системы

авления

−

)1(

)( , (2.12)

Структурная схема системы управления представлена на рис.2.2.

В заключении данного этапа строятся ЛАХ и ЛФХ передаточной функции

W .

)(

2.3. Синтез следящей системы управления

С учетом того, что измерения проводятся с помехами, управляющее воздействие

объектом (2.6) строится в форме:

)(

pWu , (2.13)

где

)(

pW =

и )()()(*

tftfyty

−

−=ε . Структурная схема системы

(2.2), (2.4), (2.5), (2.13) приведена на рис.2.3.

Задача этого этапа со-

стоит в выборе такой переда-

точной функции регулятора

, которая обеспечит бли-

зость ошибки управления

к нулю и

требуемые характеристики

замкнутой системы управле-

ния. Для решения этой задачи воспользуемся

методом динамической компенсации.

Используя уравнения (2.2), (2.4), (2.5) и (2.13) найдем выражение для ошибки

управления

)(

t =ε

)()(

tyty −

∗

⊗

Рис. 2.3. Структурная схема сле-

дящей системы

авления

⊗

)( pW

)(

)()()()](1[)(

tfpWtypWt

зз

+−=ε

∗

, (2.14)

где

)(1

)(

)()()(

pWpWp

. (2.15)

Функция )

называется передаточной функцией замкнутой системы, а функция

- передаточной функцией разомкнутой системы.

(sW

)(sW

Выбор передаточной функции регулятора определяет вид передаточной функции

замкнутой системы. Простейший подход к выбору обратной связи заключается в

том, чтобы предъявить требования к самой )W

, к примеру, потребовать выполне-

ние условия

)(1

)(

)()(

sWsW

зз

∗

== , (2.16)

где

)(

∗

)(

∗

= - соответственно, желаемые передаточные функ-

ции замкнутой и разомкнутой системы, которые формируются на основе требований

к системе управления. Преобразуем требования, предъявленные в курсовой работе,

к замкнутой системе в условия на передаточную функцию замкнутой системы.

Требование к устойчивости замкнутой системы (a) означает, что все корни харак-

теристического полинома

)()()()()()]()()()()()([)(

20121010

sbsbsbsasasbsbsbsasasas

+=∆ (2.17)

замкнутой системы (2.2), (2.4), (2.5), (2.13) должны иметь строго отрицательную

вещественную часть.

Установившаяся ошибка, вызванная воздействием (1.1), равна

)](1[))](0(1[)( asW

taaWt

зз

⋅−++−=ε

∞

. (2.18)

Ошибка может быть ограниченной при 0

≠

a , только если выполнено условие ас-

татизма

1)0(

W (2.19)

или

0)0(

−

W , (2.20)

но это возможно, только при условии, что передаточная функция разомкнутой сис-

темы имеет нулевой полюс. Если он простой, то справедливо представление

)(

)( sW

= , 1)0(

W , (2.21)

где - коэффициент усиления разомкнутого контура. Тогда используя выражения

(2.15) и (2.21), найдем

)](1[

−

=−

ksW

(2.22)

и, следовательно,

)( akt

−

∞

=ε . (2.23)

Таким образом, для выполнения требования (1.2) необходимо, чтобы коэффициент

удовлетворял условию

−

δ=

≥

. (2.24)

Установившаяся ошибка, вызванная воздействием (1.3), является гармонической

функцией с амплитудой

yзy

ajW )(1

−

ε , (2.25)

где

- частота воздействия. Таким образом, для удовлетворения требования (1.4)

необходимо, чтобы

jW δ=

≤ω− )(1

≤

. (2.26)

Установившаяся ошибка вызванная воздействием (1.5), является гармонической

функцией с амплитудой

fзf

ajW )(

ε . (2.27)

Таким образом, для удовлетворения требования (1.7) необходимо, чтобы

jW δ=

≤ω)(

≥

. (2.28)

Если передаточная функция объекта управления является минимально-фазовой и

устойчивой, то для построения желаемой передаточной функции замкнутой систе-

мы, удовлетворяющей выше перечисленным условиям часто прибегают к методу

основанному на соответствии между логарифмическими частотными характеристи-

ками разомкнутой системы и ее статическими и динамическими свойствами в замк-

нутом состоянии.

Явные зависимости )(ω

, достаточно сложны. Поэтому часто ограничива-

ются построением асимптотических логарифмических частотных характеристик.

Для примера рассмотрим произвольную минимально-фазовую передаточную функ-

цию с вещественными нулями и полюсами

)(ωϕ

∏

′′

′

ν−

kssW

)1(

)( , (2.29)

где

- положительный коэффициент усиления,

′

- положительные постоян-

ные времени,. - натуральное число (порядок астатизма). Тогда соответствующие

ЛАХ и ЛФХ даются формулами

∑∑

+ω

′′

−+ω

′

+ων−=ω

TTkL ]1)lg[(20]1)lg[(20lg20lg20)(

, (2.30)

∑∑

′′

−ω

′

ν=ωϕ

TT )arctg()arctg(

)(

. (2.31)

Асимптотическая ЛАХ есть кусочно-линейная функция, получаемая заменой в

(29) членов 20

на

]1)lg[(

+ωT











≥ωω

≤ω

,lg20

где частота

=ω называется сопрягающей.

Асимптотическая ЛФХ есть кусочно-постоянная функция, получаемая заменой в

(30) членов arctg( )ω

на











≥ω

≤ω

Нетрудно заметить, что для систем с передаточной функцией вида (2.29) по асим-

птотической ЛАХ можно восстановить асимптотическую ЛФХ и саму передаточ-

ную функцию. Данное свойство характерно для любой передаточной функции, не

имеющей нулей и полюсов в правой полуплоскости.

Преобразуем требования к замкнутой системе в ограничения на свойства лога-

рифмической амплитудной характеристики разомкнутой системы. Условие (2.21) на

отработку линейно растущего задающего воздействия сводятся к ограничению на

поведение )W

при низких частотах, близких

( ωj

≈ω

)( (2.32)

и, следовательно,

ω−=ω=ω lg20lg20)(lg20)(

ppp

kjWL . (2.33)

Иначе говоря, низкочастотная асимптота )(

L должна иметь наклон -20 дБ/дек,

причем в силу (2.24) ее уровень определяется условием

lg20lg20

−

≥

k . (2.34)

Условия (2.26), (2.28) при достаточно малых

можно заменить на

)(

−

δ≥ω

jW ,

≤

, (2.35)

jW δ≤ω)( ,

≥

(2.36)

и, следовательно,

ypp

jWL δ−≥ω=ω lg20)(lg20)( ,

≤

, (2.37)

fpp

jWL δ≤ω=ω lg20)(lg20)( ,

≥

. (2.38)

Условие (2.37) задает ограничение на поведение логарифмической амплитудной

частотной характеристики в области низких частот, а условие (2.38) - в высокочас-

тотной области.

Поведение ЛАХ в области средних частот определяет запасы устойчивости по фа-

зе и амплитуде и в значительной мере качество системы в переходном режиме (вре-

мя переходного процесса и перерегулирование). Для обеспечения приемлемых запа-

сов устойчивости наклон ЛАХ на частоте

такой, что 0)( =

обычно выбира-

ется равным -20 дБ/дек, причем длительность этого участка должна быть не менее

декады, что соответствует изменению частоты в 10 раз. Частота

называется час-

тотой среза. Значение частоты среза надо выбирать наиболее большим из всех воз-

можных для того, чтобы увеличить быстродействие замкнутой системы.

Итак, все требования, которые были сформулированы в задании курсовой роботы,

сведены к ограничениям на допустимое поведение ЛАХ разомкнутой системы (см.

рис. 2.4, где заштрихованы границы зон, в которые не может заходить ЛАХ). Оста-

ется подобрать передаточную функцию разомкнутого контура )

, для которой

эти ограничения выполнены. Если )

минимально-фазовая передаточная функ-

ция, то вначале строят асимптотическую ЛАХ, удовлетворяющую всем ограничени-

ем, а затем по ней находят саму W .

(sW

∗

(sW

∗

)(s

∗

Приведем в готовом виде сводку допустимых передаточных функций разомкну-

той системы:

-20 дБ/дек

lgδ

−

δlg20

δ− lg20

klg20

Рис. 2.4. Ограничения на допустимое поведение ЛАХ

ωlg

)(ω

1) Пусть

≤δ≤

ωδ

. (2.39)

Тогда передаточная функция

∗

)(,

ffp

(2.40)

удовлетворяет всем ограничениям. При тех же условиях допустима, но требует

меньшего усиления на частотах

≥

и обеспечивает лучшее подавление помех

передаточная функция вида

)1)(1(

)1(

)(

∗

sTsTs

sTk

, (2.41)

где

−

δ=

k ,

ωδ

µδ

T , T

1.0 T

≈

, (2.42)

а параметр

, характеризующий расположение частоты среза , может вы-

бираться в пределах 2

÷4.

/ T

µ=ω

2) Пусть

≤δ

ωδ

<δ

. (2.43)