Блюмин С.Л., Шуйкова И.А., Сараев П.В. Нечеткая логика: алгебраические основы и приложения

Подождите немного. Документ загружается.

2.1. Модели и методы ПР в условиях неопределенности 51

2.1.4. Методы принятия решений при нечеткой исходной

информации

В работе [28] рассматриваются методы принятия решений, основан-

ные на парных сравнениях альтернатив, которые выражаются в виде

нечетких отношений. Методы основаны на модели функции недомини-

руемости. В работе [8] произведена структуризация данных методов, в

результате которой выделим следующие методы теории принятия реше-

ний при нечеткой исходной информации:

– методы принятия решений с одним экспертом;

– методы принятия решений с группой экспертов, характеризуемых ве-

совыми коэффициентами;

– методы принятия решений с группой экспертов, характеризуемых

нечетким отношением нестрогого предпочтения.

Задача принятия решения с одним экспертом

Задано множество U = {u

,...,u

} возможных решений или аль-

тернатив и нечеткое отношение нестрогого предпочтения (н.о.п.) R на

множестве U сфункциейпринадлежностиµ

) ∈ [0, 1] — любое ре-

флексивное нечеткое отношение на U,такое,чтоµ

)=1,u

∈ U.

Н.о.п. задается обычно ЛПР в результате опроса экспертов, обладаю-

щих знаниями или представлениями о содержании или существе задачи,

которые не были формализованы в силу чрезмерной сложности такой

формализации или по другим причинам.

Для любой пары альтернатив u

∈ U значение µ

) понима-

ется как степень предпочтения «u

,нехужеu

»взаписиu

 u

. Ра-

венство µ

)=0может означать как то, что µ

) > 0,тоесть

с положительной степенью выполнено «обратное» предпочтение u

 u

так и то, что и µ

)=0,тоестьальтернативыu

и u

несравни-

мы. Рефлексивность н.о.п. отражает тот естественный факт, что любая

альтернатива не хуже самой себя.

Задача принятия решения заключается в рациональном выборе наи-

более предпочтительных альтернатив из множества U, на котором задано

нечеткое отношение предпочтения R.

Алгоритм решения задачи

1. Строится нечеткое отношение строгого предпочтения R

, ассоции-

рованное с R, определяемое функцией принадлежности



) − µ

),µ

) >µ

);

0,µ

)  µ

52 Приложения нечеткой логики

Это отношение может быть представлено в виде R

= R/R

,гдеR

—

«обратное» отношение (матрица отношений R

получается транспониро-

ванием матрицы отношений R).

2. Строится нечеткое подмножество U

⊂ U недоминируемых аль-

тернатив, ассоциированное с R и включающее те альтернативы, которые

не доминируются никакими другими, определяемое функцией принад-

лежности

) = min

∈U

{1 − µ

)} =1− max

∈U

{µ

)},u

∈ U.

Для любой альтернативы u

∈ U значение µ

) понимается как

степень недоминируемости этой альтернативы, то есть степень, с которой

не доминируется ни одной из альтернатив множества U; µ

)=α

означает, что никакая альтернатива u

неможетбытьлучшеu

со степе-

нью доминирования большей α;иначеговоря,u

может доминироваться

другими альтернативами, но со степенью не выше 1 − α. Рациональным

естественно считать выбор альтернатив, имеющих по возможности боль-

шую степень принадлежности множеству U

3. Выбирается та альтернатива u

∗

,длякоторойзначениеµ

∗

),мак-

симально:

∗

= arg max

∈U

Она и дает решение задачи. Если наибольшую степень недоминируемости

имеет не одна, а несколько альтернатив, то ЛПР может либо сам выбрать

одну из них, исходя из каких-либо дополнительных соображений, либо

расширить круг экспертов при формировании исходных данных задачи и

повторитьеерешение.

Пример 2.1. На множестве U из четырех альтернатив U = {u

,...,u

}

задано отношение R матрицей M

, тогда отношение R

определяется

матрицей M







100.30.7

110.80.1

0.50.51 1

0.50.50 1













0000.2

100.30

0.20 0 1

00.40 0







Для построения множества U

предварительно определяются макси-

мальные элементы в столбцах матрицы M

: m = [1; 0.4; 0.3; 1]. Множе-

ство U

определяется ветором µ

= [0; 0.6; 0.7; 0]. Так как µ

2.1. Модели и методы ПР в условиях неопределенности 53

0.7 = max µ

),тоu

∗

= u

. Если же







110.10.1

010.60.9

0.50.51 0

0.50.51 1













0100

000.10.4

0.400 0

0.401 0







m =[0.4; 1; 1; 0.4],тогдаν

=[0.6, 0, 0, 0.6]. В этом случае в качестве u

∗

может быть выбрана как альтернатива u

,такиu



Задача принятия решения с группой экспертов, характеризуемых

весовыми коэффициентами

На множестве U = {u

,...,u

} всевозможных решений (альтер-

натив) задано несколько н.о.п. Нечеткие отношения нестрогого предпо-

чтения R

получены в результате опроса каждого эксперта и заполнении

матрицы нечеткого отношения нестрогого предпочтения (н.о.п.) R

, каж-

дый элемент которой есть значение функции принадлежности µ

выражающее степень предпочтительности альтернативы u

по сравнению

с u

При µ

) > 0 u

предпочтительнее, чем u

;еслиже

)=0, то либо первая альтернатива хуже второй, либо они

несравнимы.

Лицо, принимающее решение, по-разному относится к экспертам, что

находит отражение в весовых коэффициентах λ

, 0  λ

 1,



=1,

соответствующих каждому из них.

Целью данной задачи является упорядочение совокупности альтерна-

тив U= {u

,...,u

Алгоритм решения задачи

1. Строится свертка P отношений как пересечение нечетких отноше-

ний нестрогого предпочтения экспертов

P = ∩R

) = min{µ

)};

таким образом, получается новое нечеткое отношение нестрогого пред-

почтения.

Далее с н.о.п. ассоциируется отношение строгого предпочтения

= P/P

сфункциейпринадлежностиµ



) − µ

), если µ

) >µ

);

0, если µ

)  µ

54 Приложения нечеткой логики

Далее определяется множество недоминируемых альтернатив U

функцией принадлежности

)=1− max

∈P

{µ

)},u

∈ U.

2. Строится выпуклая свертка Q отношений R

, которая определяется

как Q =



,µ



). Она является новым

н.о.п., с которым ассоциируются его отношение строгого предпочтения

и множество недоминируемых альтернатив U

. Множества U

несут дополняющую друг друга информацию о недоминируемости

альтернатив.

3. Рассматривается пересечение полученных множеств U

и U

= U

∩ U

сфункциейпринадлежности

) = min{µ

),µ

)}.

4. Выбирается та альтернатива u∗, для которой значение µ

(u∗) мак-

симально: u∗ = arg max µ

),u

∈ U .

Пример 2.2. На множестве U = {u

,...,u

} пять экспертов задали от-

ношения R

матрицами M







110.20.4

010.80.6

0.50.51 0

0.50.51 1













100.20.9

110.90.5

0.50.51 1

0.50.50 1













10.30.71

0.5110.9

0.5010.1

0.50.50.51













10.20.50

0.51 0 0.6

0.51 1 0.8

10.50.51













10.11 0.6

0.51 0.31

00.51 0

0.50 0.51







Весовые коэффициенты относительной важности экспертов с точ-

ки зрения лица, принимающего решения: λ

= λ

=0.2, λ

=0.3,

2.1. Модели и методы ПР в условиях неопределенности 55

=0.1. Свертки P и Q отношений R

определяются мат-

рицами:







100.20

0100.5

0010

0.500 1













10.34 0.49 0.62

0.51 0.67 0.71

0.45 0.45 1 0.39

0.60.45 0.51







Множества P

, Q

определяются матрицами







000.20

0000.5

0000

0.500 0













000.04 0.02

0.16 0 0.22 0.71

0.45 0.45 1 0.39

0.60.45 0.51







Множества U

, U

определяются векторами ν

=[0.5, 1, 0.8, 0.5],

=[0.84, 1, 0.78, 0.74], откуда µ

=[0.5, 1, 0.78, 0.5].

Значит, u∗ = u

. 

Задача принятия решения с группой экспертов, характеризуемых

нечетким отношением нестрогого предпочтения между ними

Можно рассмотреть задачу принятия решений с группой экспертов,

характеризуемых не весовыми коэффициентами, а при помощи еще од-

ного н.о.п. N, заданного на множестве E экспертов с функцией при-

надлежности µ

),e

∈ E, значения которой означают степень

предпочтения эксперта e

по сравнению с экспертом e

Алгоритм решения задачи

1. С каждым R

ассоциируются R

и U

, вводится обозначе-

ние µ

)=µ

(

),i=1,...,n, k =1,...,m. Тем самым задает-

ся нечеткое соответствие Φ между множествами E и U.

2. Строится свертка Γ в виде композиции соответствий Γ=Φ

NΦ.

Причем, результирующее отношение Γ определяется как максминное про-

изведение матриц Φ

, N, Φ. То есть, получается единое результирующее

отношение, полученное с учетом информации об относительной важно-

сти н.о.п. R

. С отношением Γ ассоциируется отношение Γ

имножество

3. Корректируется множество U

до множества U



cфункцией

принадлежности µ

) = min{µ

),µ

)}.

4. Выбирается та альтернатива, для которой значение функции при-

надлежности скорректированного нечеткого подмножества U



недоми-

нируемых альтернатив максимально.

56 Приложения нечеткой логики

2.2. Нечеткие реляционные уравнения

Элементы теории нечетких реляционных уравнений можно найти в

[39,49, 56–58].

Пусть X, Y , Z — дискретные четкие множества конечной мощности

m, n и k соответственно,



Q(X, Y ),



R(Y,Z),



S(X, Z) — нечеткие соответ-

ствия и пусть имеется композиция



Q ◦



R =



S, (2.8)

где ◦ = (max,T) или ◦ = (min,I) при I(x, y)=I

T,N

(x, y). (2.8) соответ-

ствует матричному уравнению

Q ◦ R = S, (2.9)

где Q

n×m

, R

m×k

, S

n×k

— матричные представления



R и



S соответ-

ственно. Прямая задача нахождения представления нечеткого соответ-

ствия S при заданных Q, R и правиле композиции тривиальна. Рассмот-

рим так называемую обратную задачу для нечетких соответствий, т.е.

(i) определение Q при известных R, S и ◦;

(ii) определение R при известных Q, S и ◦.

По аналогии с терминологией матричной алгебры, будем называть

первое уравнение левым, а второе, соответственно, правым нечетким

реляционным уравнением (Fuzzy Relational Equation, FRE). Заметим, что

в силу коммутативности t-нормы при ◦ = (max,T) задача (ii) сводится

к (i), т.е. в этом случае достаточно рассмотреть только левые уравнения.

Методы решений нечетких реляционных уравнений различаются в

зависимости от размерностей Q, R и S.

2.2.1. Необходимые сведения

1. Введем на множестве матриц фиксированного размера отношение

порядка:

)  (b

) ⇔ a

 b

, ∀i, j.

Данное отношение частично упорядочивает множество матриц (следова-

тельно, и множество векторов): не любые две матрицы можно сравнить

между собой.

2. Объединением двух матриц A =(a

) и B =(b

) будем называть

матрицу C = A ∪ B =(c

),гдеc

= a

∪ b

= max{a

2.2. Нечеткие реляционные уравнения 57

Пересечением двух матриц A =(a

) и B =(b

) будем называть

матрицу C = A ∩ B =(c

),гдеc

= a

∩ b

= min{a

3. Обычно нечеткое реляционное уравнение имеет не единственное

решение. Максимальным (минимальным) решением будем называть та-

кое решение X

,чтоX

 X

(соответственно, X

 X

)длявсехX

из

множества решений.

4. Множество решений простейшего уравнения (известные представ-

ляют собой числа из L =[0, 1]) может быть пустым, единственным из L

или быть отрезком, принадлежащим L.

Структура множества решений (если оно существует) остальных не-

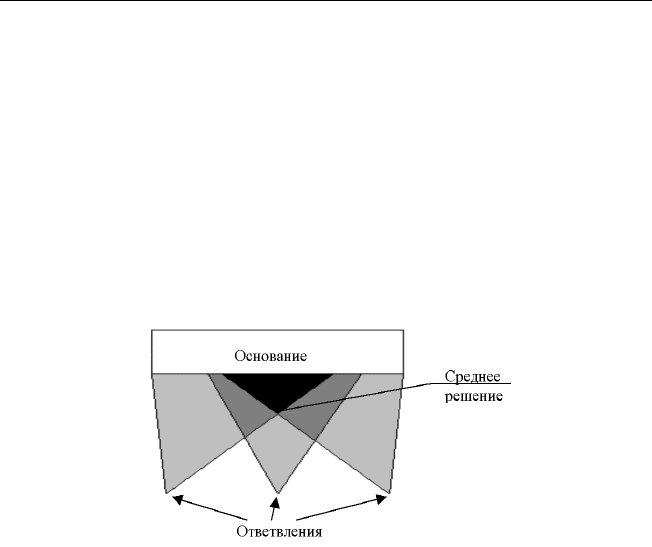
четких реляционных уравнений приведена на рисунке 2.21. Для max-T

Рис. 2.21. Общая структура решения

илевыхmin-I уравнений основание представляет собой максимальное

решение, ответвления — множество минимальных. Для правых min-I

уравнений основание — минимальное решение, ответвления — множе-

ство максимальных.

5. Множество решений нечетких уравнений выпукло упорядочено,

т.е., если (x

) и (y

) — два различных решения и x

 z

 y

для

любых i и j,торешениембудети(z

). Следовательно, основной задачей

является отыскание основания и всех ответвлений данного уравнения.

6. Схемы рассуждений, доказательств и свойства различных типов

уравнений схожи, поэтому будем рассматривать только один тип урав-

нений (чаще всего левые min-I уравнения). Результаты для остальных

будут приведены без доказательств. Самостоятельное получение этих ре-

зультатов может служить как тренировкой для читателя, так и проверкой

усвоения материала.

Рассуждения для max-T илевыхmin-I уравнений идентичны, для

58 Приложения нечеткой логики

правых min-I уравнений они носят двойственный характер (т.е. макси-

мум заменяется на минимум, наибольшее решение на наименьшее и т.п.).

Конечные результаты для всех типов уравнений приведены в конце этого

раздела.

2.2.2. Простейшие нечеткие реляционные уравнения

Рассмотрим простейший случай, когда известные в обеих частях

представляют собой числа из L =[0, 1]. Требуется найти x, удовлетворя-

ющий одному из уравнений при a, b ∈ L:

T (x, a)=b, (2.10)

I(x, a)=b, (2.11)

I(a, x)=b. (2.12)

Решения (2.10)–(2.12) могут быть найдены как пересечения решений

двух соответствующих неравенств: например, T (x, a)  b и T (x, a)  b

для (2.10). Введем ряд так называемых разностных операторов:

−

(a, b) = min{z ∈ L | T (z,a)  b},

(a, b) = max{z ∈ L | T (z,a)  b},

−

(a, b) = min{z ∈ L | I(z,a)  b},

(a, b) = max{z ∈ L | I(z,a)  b},

−

(a, b) = min{z ∈ L | I(a, z)  b},

(a, b) = max{z ∈ L | I(a, z)  b}.

Предложение 2.1. T

(a, b), I

(a, b) и I

−

(a, b) существуют при любых

a, b ∈ L.

Доказательство. Можно указать по крайней мере одно значение z,при

котором выполняются входящие в операторы неравенства: z =0для пер-

выхдвухиz =1для последнего. Частные функции t-нормы, t-конормы

и импликатора непрерывны, откуда следует возможность указать макси-

мальный (минимальный) элемент, удовлетворяющий неравенству.

Предложение 2.2. Если a<b,тоT

−

(a, b)=. Если a>b,тогда

−

(a, b)=. Если b<N(a),тоI

(a, b)=.

2.2. Нечеткие реляционные уравнения 59

Доказательство. Докажем утверждение для первого оператора, для ос-

тальных рассуждения аналогичны. Пусть T

−

(a, b) = ,тогда∃z

∈ L,

такое, что T (z

,a)  b. По свойству PT1 имеем T (z

,a)  a. Принимая

во внимание предыдущее неравенство, имеем b  a. Полученное проти-

воречиедоказываетпредложение.

Из предложений 2.1, 2.2 и определений разностных операторов сле-

дует, что неравенства T (x, a)  b, I(x, a)  b и I(a, x)  b имеют реше-

ния [0,T

(a, b)], [0,I

(a, b)] и [I

−

(a, b), 1] соответственно. Решения двой-

ственных им неравенств, как следует из предложения 2.2, существуют

при a  b, a  b и b  N (a); ими будут отрезки [T

−

(a, b), 1], [I

−

(a, b), 1]

и [0,I

(a, b)].

Пересечение соответствующих решений неравенств является решени-

ем (2.10)-(2.12). Кроме того, предложение 2.2 дает необходимые и доста-

точные условия их разрешимости. Таким образом, решениями уравнений

(2.10)-(2.12) будут

−

(a, b),T

(a, b)], если b  a,(2.13)

−

(a, b),I

(a, b)], если a  b,(2.14)

−

(a, b),I

(a, b)], если N(a)  b. (2.15)

Если условия предложения 2.2 выполняются, то уравнение имеет пустое

множество решений.

Предложение 2.3. Если каждое из уравнений вида (2.10)-(2.12) разре-

шимо, то

T (T

(a, b),a)=b и T (T

−

(a, b),a)=b,

I(I

(a, b),a)=b и I(I

−

(a, b),a)=b,

I(a, I

(a, b)) = b и I(a, I

−

(a, b)) = b.

Доказательство. Докажем для левого min-I уравнения первое равенст-

во. Пусть δ = I

(a, b). В силу непрерывности функции I(x, a) существует

такое c

∈ L,чтоI(c

,a)=b. Так как функция I(x, a) невозрастающая,

то выполняется I(c

,a)  I(c

,a)=b для любого c

∈ L, c

Максимальный элемент c

, удовлетворяющий равенству

I(c

,a)=I(c

,a), существует и будет равен δ. При I(c

,a) <I(c

,a)

элемент c

есть максимальный элемент, удовлетворяющий неравенству

I(c

,a)=b,т.е.c

= δ.

Доказательство остальных равенств аналогично приведенному.

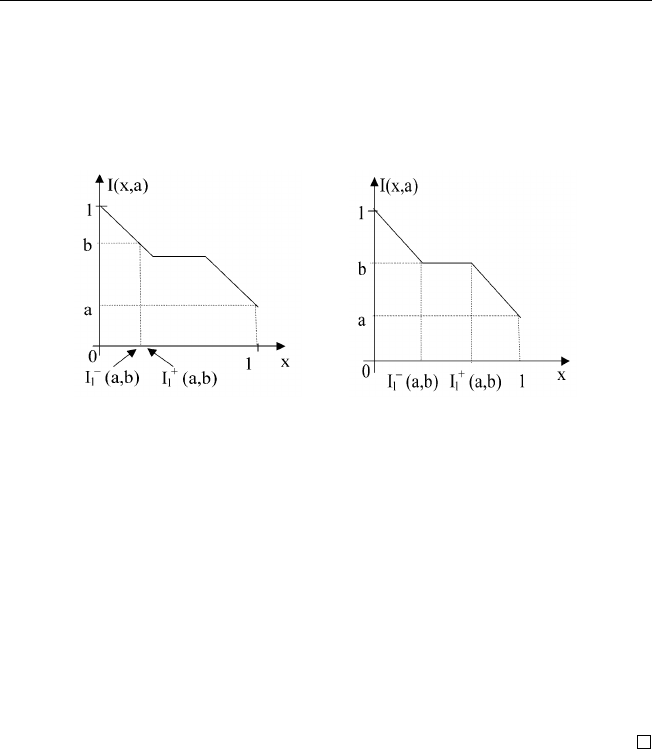
60 Приложения нечеткой логики

Несколько слов о форме определения разностных операторов. На

рис. 2.22 показан геометрический смысл разностных операторов левых

min-I уравнений при единственном решении и отрезке решений. Опера-

ции min и max при задании разностных операторов используются как

для определения единственного решения, так и концов отрезка.

а) единственное решение б) отрезок решений

Рис. 2.22. Определение разностных операторов

Конкретный вид разностных операторов для часто встречающихся

t-норм и импликаторов приведен в таблицах 2.4-2.6.

Пример 2.3. Приведем примеры разрешимых и неразрешимых уравне-

ний.

a) Уравнение T (0.2,x)=0.9 имеет пустое множество решений, т. к.

0.2 < 0.9.

b) Уравнение T (x, 0.5) = 0.5 при T = min(x, y) разрешимо, т. к.

0.5  0.5. T

−

(0.5, 0.5) = 0.5, T

(0.5, 0.5) = 1, следовательно, мно-

жеством решений является отрезок [0.5, 1].

2.2.3. Полиномиальные уравнения

Нечеткое реляционное уравнение вида

,...,x

) ◦ (a

,...,a

)

= b или

,...,a

) ◦ (x

,...,x

)

= b

при заданных {a

}, b и ◦,будемназыватьполиномиальным. Символ T в

левых частях — символ транспонирования.