Блюмин С.Л., Шуйкова И.А., Сараев П.В. Нечеткая логика: алгебраические основы и приложения

Подождите немного. Документ загружается.

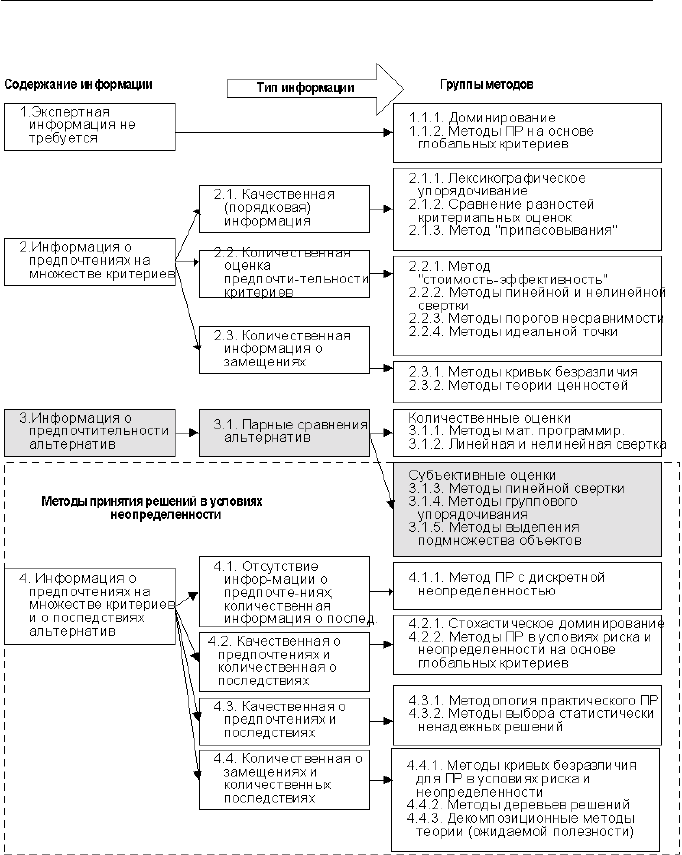
2.1. Модели и методы ПР в условиях неопределенности 41

Рис. 2.19. Классификация методов ПР на основе содержания экспертной

информации

42 Приложения нечеткой логики

а далее объекты просто упорядочиваются по убыванию значений это-

го ранжирующего фактора. В моделях второй группы, использующих

комбинаторно-логические и теоретико-графовые методы, оценивают-

ся показатели не отдельных объектов, а всего упорядочивания в целом,

и выбирается упорядочивание, максимизирующее некоторый функционал

качества. Оценок важности при этом не делается. Рассмотрим некоторые

модели первой группы.

Пусть задано некоторое фиксированное множество объектов

X = {x

,...,x

}, которые сравниваются попарно с точки зрения их

предпочтительности, желательности, важности и т.п., а результаты запи-

сываются в виде матрицы парных сравнений A = ||a

n×n

, отражающей

возникающее бинарное отношение предпочтения/безразличия на множе-

стве X. Симметричные элементы матрицы парных сравнений a

и a

должны выбираться равными, если соответствующие объекты равноцен-

ны или несравнимы (x

∼ x

);еслижеx

,тодолжнобытьa

Кроме того, на элементы матрицы A обычно накладываются дополни-

тельные калибровочные ограничения , однозначно связывающие попарно

симметричные элементы a

, a

. Приведем основные типы калибровок.

1. Простая структура (ПС).

∀i, j, i = ja







1, если x

;

0, если x

;

1/2, если x

∼ x

Интерпретация: a

- индикатор факта превосходства одного объекта над

другим или их равноценности (несравнимости).

2. Турнирная калибровка (Т).

∀i, j a

 0; a

+ a

= c.

Интерпретация: a

— число очков, набранных игроком x

во всех встре-

чах с игроком x

;числоc = const при этом может интерпретироваться

как количество таких встреч. Нередко дополнительно постулируется це-

лочисленность матрицы.

3. Кососимметрическая калибровка (К).

∀i, j a

+ a

=0.

Интерпретация: объект x

превосходит в сравнении объект x

на a

4. Степенная калибровка (С).

∀i, j a

> 0; a

· a

=1.

2.1. Модели и методы ПР в условиях неопределенности 43

Интерпретация: объект x

превосходит в парном сравнении объект x

раз.

5. Вероятностная калибровка (В).

∀i, j 0  a

 1; a

+ a

=1.

Интерпретация: a

— вероятность превосходства x

над x

Помимо приведенных калибровок для полноты анализа можно вве-

сти еще и произвольную взвешенную структуру (ВС), в рамках которой

предполагается обычно только неотрицательность матрицы A,самиже

ее элементы могут интерпретироваться по-разному.

Переход от матрицы A, заданной в некоторой калибровке, к отка-

либрованной по-иному матрице B возможен не всегда, но лишь при со-

блюдении некоторых дополнительных содержательных условий и нередко

сопряжен с потерей важной информации. Вопрос о возможности перехо-

дакматрицесдругойкалибровкойиопутяхтакогопереходавсякийраз

должен рассматриваться с учетом содержательных особенностей задачи.

Схемы и направления подобных переходов приведены в таблице 2.1.

Таблица 2.1.

Преобразование калибровок

Тип перехода Возможные способы реализации

ВС→ Т b

= a

+ (max

i,j

− s

)/2;

=(a

· max

i,j

)/s

; s

= a

+ a

;

Т→ К b

= a

− a

; b

=(a

− a

)/2;

K→ T b

= a

(signa

+1)/2 + (max

i,j

−|a

|)/2;

= c(a

+ max

i,j

); c>0;

K→ С b

= r

; r>1;

С→ К b

= log

; r>1;

В, Т→ С b

= a

;

C→ В, Т b

= a

/(1 + a

);

Т→ В b

= a

/(a

+ a

);

В→ T b

= c · a

; c>0;

ВС,Т,В,К,С→ ПС b

=[sign(a

− a

)+1]/2.

Каждая из моделей линейного упорядочивания требует для матриц

парных сравнений определенных калибровочных ограничений.

1. Модели спортивного типа: ∀i =

1,n s



i=j

. Такое название

44 Приложения нечеткой логики

исторически укоренилось за целой группой сходных моделей, в которых в

качестве ранжирующего фактора используется набранная объектом «сум-

ма очков». Обрабатываемая матрица А может иметь калибровку типа Т,

ПС или К (таблица 2.2).

Таблица 2.2.

Модели спортивного типа

Название

модели

ПР

Математическая

модель

Положительные

характеристики

Недостатки

модели

Турнирная

модель

Объекты упорядочи-

ваютсяпоубыванию

Простота полу-

чения результа-

та. Выполняют-

ся свойства

Вычисление

количествен-

ных

Модель

последова-

тельного

вычле-

нения

лидеров

В качестве лучшего

(лидера) выбирается

объект с max

, вы-

черкивается i-я стро-

ка и i-й столбец,

вновь выбирается ли-

дер и т.д.

«Инвариантность

ксдвигу»,«Ин-

вариантность к

растяжению»,

«Положитель-

ная реакция».

оценок мо-

дель не

предполага-

ет.

Модель

последо-

вательной

дихотомии

Множество X разби-

вается на два слоя —

слойсбольшимиs

слойсменьшимиs

т.д. делится каждый

слой.

Простота полу-

чения результа-

та.

Не обладает

свойствами

«Устой-

чивость в

малом», «По-

ложительная

реакция».

2. Модель интегральной степени превосходства является близкой

к моделям спортивного типа; применяется для кососимметрических мат-

риц. Вводится понятие интегральной степени превосходства

Φ(x



t=1

− a

)

, оценивающей превосходство x

над x

в сравнении с прочими объ-

ектами. Когда интегральная степень превосходства задана, ее мож-

но представить в виде

Φ(x

)=f(x

) − f(x

), при этом ∀if(x

2.1. Модели и методы ПР в условиях неопределенности 45



j=1

Φ(x

),гдеf — функция полезности на X, и объекты предлага-

ется упорядочивать по убыванию ее значений.

К недостаткам модели можно отнести введение весов объектов —

коэффициентов λ

, — однако таких весов заранее задано быть не может.

Модель сводится к турнирной и самостоятельного интереса не имеет.

3. Модель функции доминируемости ориентирована на обработку

нечетких отношений предпочтения, т.е. a

∈ [0, 1]. Применяется для ка-

либровок Т, К. Функция доминируемости l(x

) = max

j=i

характеризует

максимальную силу, с которой объект x

доминируется остальными объ-

ектами множества X. При l(x

)=0— абсолютно не доминируется, при

l(x

)=1— абсолютно доминируется, при 0 <l(x

) < 1 — слабо домини-

руется. Объекты упорядочиваются по убыванию соответствующих зна-

чений функции m(x

)=1− l(x

). В [28] используются другие способы

получения l(x

). Возможно использование значений в качестве коли-

чественных оценок важности объектов. Модель обладает свойствами

«устойчивость в малом», «положительная реакция», «инвариантность к

сдвигу», «инвариантность к растяжению».

4. Модель Брэдли-Терри пригодна для простых структур без равно-

ценных элементов и целочисленных турнирных матриц.

Каждому объекту сопоставляется его «сила» π

, причем предполагает-

ся, что вероятность превосходства в парном сравнении P (x

) прямо

пропорциональна π

: P (x

)=π

/(π

+ π

)=1− P (x

). Для

каждой пары (i, j) проводится k независимых актов парных сравнений.

Окончательно получается:











/π

= k



j=1

(π

+ π

)

−1

,i= 1,n;



j=1

=1.

Система может быть решена итерационно. После вычисления всех π

объекты упорядочиваются по их убыванию.

Получаемые компоненты нормализованного вектора π могут служить

количественными оценками важности объектов. Выполняются свойства

«инвариантность к сдвигу», «инвариантность к растяжению».

5. Модель Бэржа-Брука-Буркова применяется для обработки про-

стых структур, матриц с турнирной и степенной калибровками.

Каждому объекту x

ставится в соответствие цепочка так называемых

интегрированных сил, в которой сила k-го порядка p

определяется как

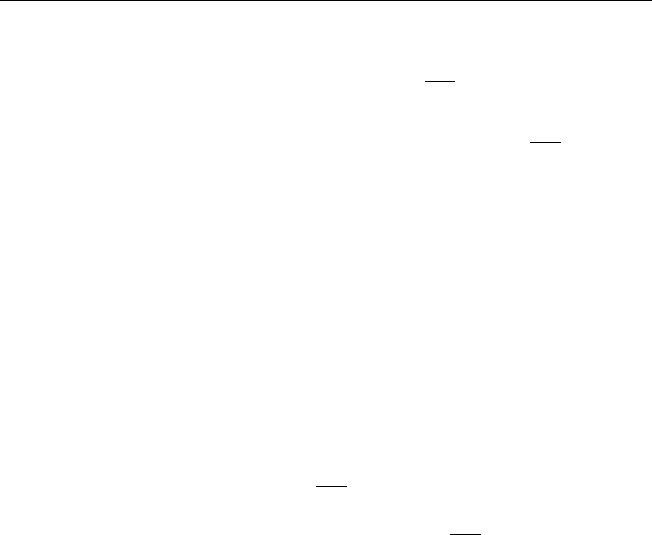
46 Приложения нечеткой логики

сумма элементов i-й строки в матрице A



j=1

, ||a

n×n

= A

; ∀i = 1,n,k =1, 2,...

При k →∞имеет место lim

k→∞



)=π, i = 1,n,гденор-

мализованный собственный вектор π =(π

,...,π

) матрицы A отве-

чает максимальному по модулю собственному числу теоремы Перрона-

Фробениуса. Модель обладает свойствами: «инвариантность к растяже-

нию», «устойчивость в малом», «транспонируемость» (при a

=1). По-

лучаемые значения компонент собств. вектора могут служить оценкой

важности объектов.

6. Стохастическая модель Ушакова предложена для обработки мат-

риц, заданных в степенной и вероятностной калибровках. Матрица A

преобразуется в вероятностную матрицу P ,гдеp

— вероятность пре-

восходства x

над x

. При вероятностной калибровке P = A

При степенной калибровке p

= a

/(1 + a

)

−1

,i= j.

Строится стохастическая матрица

P = ||˜p

n×n

˜p

=1−



i = j ˜p

,i,j= 1,n, ˜p

= p

/(n − 1),i= j;

= 



i = j



,i,j= 1,n,

где 

— минор получаемый из det(E −

P ) вычеркиванием i-й строки и

j-го столбца.

Упорядочивание x

производится по p

. Обладает свойствами «устой-

чивость в малом», «положительная реакция». Получаемые компоненты

финального распределения могут использоваться в качестве количествен-

ных оценок важности объектов.

Не обладает свойствами «инвариантность к растяжению», «инвари-

антность к сдвигу».

7. Модель равномерного сглаживания применяется для положитель-

ных матриц с турнирной или степенной калибровкой. По аксиоме Льюса

для калибровки Т имеет место: ∀i, j π

/π

= a

и при этом

= π



j=1







j=1

/π





−1







j=1





−1

Обозначая ∀i, j z

=lnb

,получаем∀i, j z

= z

+ z

,такчто

матрица Z = ||z

n×n

может быть восстановлена по любой строке.

2.1. Модели и методы ПР в условиях неопределенности 47

В данной модели от исходной матрицы A необходимо перейти к мат-

рице Z и построить n различных матриц Z

(1)

,...,Z

(n)

, полагая, что

матрица Z

(k)

порождается k-й строкой матрицы Z по ранее приведенной

формуле.

Z =(1/n)



(i)

,причем∀i, j z

=(1/n)



k=1

+ z

). Про-

делав преобразования ∀i, j

=expz

, a

= cb

(1 + b

)

−1

,витоге

получим π





j=1



−1

Обладает свойствами «инвариантность к растяжению», «транспониру-

емость», «устойчивость в малом», «положительная реакция». Получаемые

коэффициенты можно использовать для количественной оценки важно-

сти объектов.

Выбор модели упорядочивания с теми свойствами, которые особен-

но желательны в данном конкретном случае, представляется весьма по-

лезным в системах поддержки принятия решений. Модели типа: модель

функции доминируемости, Брэдли-Терри, Бержа-Брука-Буркова, стоха-

стическая модель Ушакова, модель равномерного сглаживания предлага-

ют гораздо более убедительные доводы в пользу соответствующих опти-

мальных упорядочиваний. Модель Брэдли-Терри пригодна для простых

структур и целочисленных турнирных матриц, которые не учитывают

неточность, неопределенность в оценках экспертов. Стохастическая мо-

дель Ушакова скорее ориентирована на вероятностный класс неопреде-

ленностей, в отличие от нее модель Бержа-Брука-Буркова и модель функ-

ции доминируемости позволяют учитывать неопределенность явлений, не

поддающихся измерению со сколь угодно большой точностью и с учетом

нечеткости соответственно. Модель равномерного сглаживания не обла-

дает свойством «инвариантность к сдвигу», что не позволяет экспертам

производить неполные сравнения. В [4] утверждается, что модель Бержа-

Брука-Буркова также не обладает свойством «инвариантность к сдвигу»,

однако в [30] указан подход к выявлению приоритетов для неполной

матрицы на основе данной модели. Таким образом, для линейного упоря-

дочивания в условиях неопределенности предпочтительнее пользоваться

моделями функции доминируемости и Бержа-Брука-Буркова. Рассмотрим

методы ПР, ориентированные на выделенные модели.

2.1.3. Метод анализа иерархий

При принятии управленческих решений и прогнозировании возмож-

ных результатов лицо, принимающее решение, обычно сталкивается со

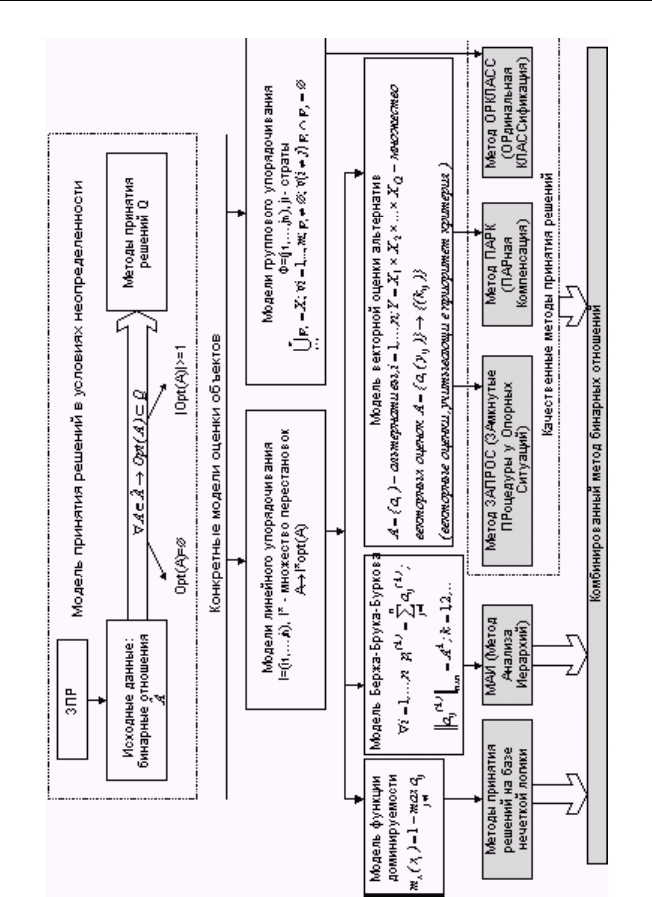
48 Приложения нечеткой логики

Рис. 2.20. Классификация моделей ПР в условиях неопределенности

2.1. Модели и методы ПР в условиях неопределенности 49

сложной системой взаимозависимых компонент (ресурсы, желаемые ис-

ходы или цели, лица или группа лиц и т.д.), которую нужно проанали-

зировать [30]. Метод анализа иерархий (МАИ) развивает модель Бержа-

Брука-Буркова [4]. Принимая решение, группа экспертов производит де-

композицию сложной проблемы — определяет ее компоненты и отноше-

ния между ними. Получается модель реальной действительности, постро-

енная в виде иерархии. Вершина иерархии — общая цель, далее распола-

гаются подцели, затем силы, которые влияют на эти подцели, люди, их

цели, политики, стратегии, и, наконец, исходы, являющиеся результата-

ми стратегий. На следующем этапе решения сравниваются уже отдель-

ные компоненты иерархии между собой. В результате может быть вы-

ражена относительная степень интенсивности взаимодействия элементов

в иерархии. Затем эти суждения выражаются численно. В завершении

анализа проблемы МАИ включает процедуры синтеза множественных

суждений, получения приоритетности критериев и нахождения альтерна-

тивных решений. Таким образом, основные этапы принятия решения с

помощью МАИ следующие:

• построение иерархии рассматриваемой проблемы;

• парное сравнение компонент иерархии;

• математическая обработка полученных суждений.

В наиболее элементарном виде иерархия строится с вершины (с точ-

ки зрения управления — целей), через промежуточные уровни (критерии,

от которых зависят последующие уровни) к самому низкому уровню (ко-

торый обычно является перечнем альтернатив). Существуют несколько

видов иерархий: доминантные, холлархии, китайский ящик и т.д. Наибо-

лее часто применяется первый тип иерархий (таблица 2.3).

Парные сравнения проводятся в терминах доминирования одного из

элементов над другим. Эти суждения затем выражаются в целых числах.

Если элемент А доминирует над элементом Б, то ячейка матрицы, соот-

ветствующая строке А и столбцу Б, заполняется целым числом, а ячейка,

соответствующая строке Б и столбцу А, заполняется обратным к нему

числом (дробью). В МАИ предложена шкала относительной важности

элементов иерархии.

Все матрицы в МАИ должны быть обратно симметричны, т.е.

=1/a

. По главной диагонали матрицы заранее ставятся единицы,

т.к. альтернатива равноценна самой себе. Для заполнения каждой мат-

рицы размером n × n достаточно произвести только n(n − 1)/2 сужде-

ния. Составление таких матриц проводится для всех уровней и групп в

50 Приложения нечеткой логики

иерархии. Причем полученные матрицы должны быть согласованы для

достоверного решения. Согласованность проявляется в числовой (карди-

нальной согласованности) и транзитивной (порядковой согласованности).

Согласованность матрицы можно проверить.

Таблица 2.3.

Шкала относительной важности МАИ

Интенсивность относи-

тельной важности

Определение

1 Равная важность

3 Умеренное превосходство одного над дру-

гим

5 Существенное или сильное превосходство

7 Значительное превосходство

9 Очень сильное превосходство

2,4,6,8 Промежуточные решения между двумя

соседними суждениями

Обратные величины при-

веденных выше чисел

Еслиприсравненииодногопараметрас

другим получено одно из вышеуказанных

чисел, то при сравнении второго парамет-

ра с первым получим обратную величину

Вычислять вектор приоритета (собственный вектор) для каждой мат-

рицы парных сравнений можно разными способами [30]. В зависимо-

сти от выбранного способа в задаче может наблюдаться большая или

меньшая погрешность. Наиболее обоснованный результат получается при

применении теоремы Перрона-Фробениуса. На последнем этапе обработ-

ки полученные векторы приоритетов синтезируются, начиная со второго

уровня вниз. Локальные приоритеты перемножаются на приоритет соот-

ветствующего критерия на вышестоящем уровне и суммируются по каж-

дому элементу в соответствии с критериями, на которые воздействует

этот элемент. Каждый элемент второго уровня умножается на единицу,

т.е.навесединственнойцелисамоговерхнегоуровня.Этодаетсостав-

ной, или глобальный, приоритет того элемента, который затем использу-

ется для взвешивания локальных приоритетов элементов, сравниваемых

по отношению к нему как к критерию и расположенных уровнем ниже.

Процедура продолжается до самого нижнего уровня.