Блинова И.В., Попов И.Ю. Случайные события, случайные величины
Подождите немного. Документ загружается.

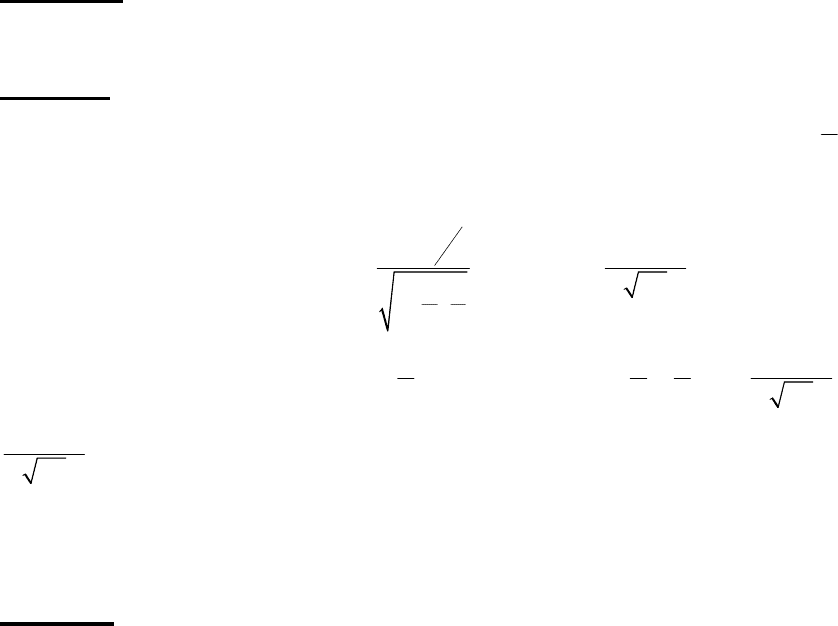
41
Пример 2
. Сколько раз достаточно подбросить игральный кубик, чтобы с
вероятностью 0,5 можно было ожидать, что выпадение шестерки будет
наблюдаться не менее 50 раз.
Решение. Предположим, что кубик подбрасывается
n
раз, а X - число
выпадений шестерки. Вероятность выпадения шестерки равна
1
6
p
=
. По
формуле (4.17) находим:
()
50
300
6
0,5
5
11
65
(50 )
n
n
n
n
PX ФФ Ф
⎛⎞
⎜⎟
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎜⎟
⎝⎠
−
−
+∞ − = −
⋅⋅
≤<+∞ .
По условию задачи
1
2
(50 )PX
≤
= . Следовательно,
11 300
22
5
n
Ф
n
⎛⎞
⎜⎟
⎝⎠
−
+
или
300
0
5
n
Ф
n
⎛⎞
⎜⎟
⎝⎠
−
=
. Откуда 300n ≈ , т.е. примерно необходимо сделать около 300
бросаний игрального кубика.
Задачи.
1. Случайная величина X распределена по нормальному закону с
математическим ожиданием 0 и дисперсией 1. Вычислить вероятность
попадания этой случайной величины в интервал
()
2, 4 . Доказать, что
(0,5 0,1) (1 2)
P
XPX−<<− > <<.
2. Случайная величина X распределена по нормальному закону с
математическим ожиданием 5 и дисперсией 4. Определить вероятность
попадания случайной величины
X в интервал a)
(
)
0,6 , b)
()
2, 2− .
3. При изготовлении детали наблюдается отклонение ее веса X от
номинального, равного 400
X
грm
=
. Считая, что случайная величина X
распределена по нормальному закону со средним квадратическим
отклонением равным 0,5 гр., определить, какую точность веса изделия
можно ожидать с вероятностью 0,9?
4. Длина изготавливаемого изделия удовлетворяет ГОСТу, если отклонение
его длины
X от номинальной 5
X
смm
=
, не превосходит по абсолютной
величине 0,1
м
м . Случайная величина X распределена по нормальному
закону со среднем квадратическим отклонением равным
0,05
м
м .
Определить вероятность изготовления изделия удовлетворяющего ГОСТу.
42
Ответы
1. п. 1.1.
1)
0,2667; 2) 0,019; 3) 0,00987; 4) 0,1863; 5) {0,1,2,...,30}
Ω
= ;
6) Каждый шахматист может занять любое место в турнире. Если обозначить
через
m
S m ого− шахматиста, то пространство элементарных событий
можно представить как совокупность упорядоченных троек:
,,
{( ) / , , 1,2,...,8, , , }
ij
k
SS S ijk i ji kj kΩ= = ≠ ≠ ≠ . Общее число таких троек,
т.е. общее число элементарных событий, связанное с распределением первых
трех призовых мест, равно
3
8
336
A
=
.
7) a) Элементарными событиями опыта являются упорядоченные пары чисел
(, )
ij, первое из которых i - число очков, выпавших на первой игральной
кости, а
j
- на второй. {( , ) / , 1, 2,...,6}ij ij
Ω
===
{(1,1),(1,2),...,(1,6),(2,1),(2,2),...,(2,6),...,(6,1),(6,2),...,(6,6)}. Общее число
элементарных событий
2
636
=
. b) аналогично a),
{(,,)/,, 1,2,...,6}
ijk ijkΩ= = = {(1,1,1), (1,1, 2), ... , (6, 6, 5), (6, 6, 6)} . Общее число
элементарных событий
3
6 216= .
8) Элементарные события опыта можно представить двухэлементными
подмножествами множества, составленного из чисел 1, 2, 3, 4, 5, 6.
{(1, 2) , (1, 3) , (1, 4), (1, 5), (1, 6), ( 2, 3) , ( 2, 4) , ( 2, 5) , ( 2, 6),Ω=
(3, 4),(3,5),(3,6),(4,5),(4,6),(5,6)}. Общее число элементарных событий равно
2
6
15C = . 9) Элементарными событиями являются все положительные
действительные числа, (0, )Ω= +∞ .
1. п. 1.2.
1)
а) общее число исходов
3
28
=
, благоприятный один,
1
8
p = ; b)
A
={герб
выпадает не более двух раз},
A
={все три раза выпадет герб}.
17
88
() 1 () 1PA PA ==− =−
.
2)
7
1
10
, a)
1
10
, b)
4
1
10
, c)
4
1
10
. 3)
7
2!2!
10
11!
p
−
== . 4) a)
1
0,0083
5!
p ≈= , b)
42!3!
0, 4
5!
p
⋅⋅
=
= . 5)
111
444
3
52
0,0029
CCC
p
C
⋅
⋅
≈
= ,
111
344
3
50
0,00245
CCC
p
C
⋅⋅
≈
= . 6)
121
55
3
8
13
0,01166
CC C
p
C
⋅⋅
≈
= .
1. п. 1.3.
1)
(2 / 3) 2
3
l
p
l
== . 2)
/5 /5 2
5
ll
p
l
+
=
= .
3) а)
1/64 1
164
A
S
p
S
Ω
=== , b)
1
4
1
64
116
A
S
p
S
Ω
⋅
=
== , c)
3
4
A
S
p
S
Ω
== .
43
4) a)
2
1
31
6
0,145
113
55
22
A
S
p
S
π
Ω
⋅⋅⋅
=≈
⋅⋅ ⋅
= , b)
2
13
5
32
0,6
13
55
22
A
S
p
S
π
Ω
⎛⎞
⎜⎟
⎜⎟
⎝⎠
⋅−
=≈
⋅⋅ ⋅
= .
5)
2
1
0,049
64
A
S
p
S
π
Ω
⋅
=≈
=
. Примечание. Круг радиуса 1 находится внутри
квадрата, если его центр располагается не ближе чем на единицу от границы
квадрата, покрывает центр квадрата, если отстоит от последнего не далее,
чем на единицу.
6)
2
2
25 11
11
36
30
AAA
SS S
S
p
SS S
Ω
ΩΩ Ω
−
==−=−=
=
.
2. п. 2.1.
1)
A
и
A
; 2) a) B , b)
A
B , c)
A
B , d)
A
BC ABC
+
; 3) a)
A
B= , b) BCA;
4) a) да, если
A
и B совместны, нет в противном случае, b) нет, c) да, d) нет;
5) a)
A
CE+=, b)
A
CK= , c)
E
FG
=
, d) GEE
+
= , e) GE G= ,
f)
BD H= , g) EK E+=; 6) a)
123
A
AAA
=
, b)
123
BAAA= ,
c)
1
123123123123123123 23
CAAAAAAAAAAAAAAAAAAAAA++++++= ,
d)
12 3 1 23 12 3 12 3 123 1 23 12 3
D AAA AAA AA A AAA AAA AAA AAA++++++= ,
e)
123 12 3 123 123
E
AAAAAAAAAAAA+++= ,
f)
123 123 123 123
FAAAAAAAAAAAA+++= , g)
123
GAAA
=
;
7) a) нет, b) нет, c) да, d) нет; 8) a)
5
1234 6
A
AAAAA, b)
5
23
A
AA,
c)
()()
4623
A
AAA++, d)
55
1234 6 1 2 3 4 6
A
AAAAA A A A A A A
=
+++++.
2. п. 2.2.
1)
a)
1
72
, b)
1
72
, c)
1
36
; 2) a) 0,018; b) 0,321; 3)
1
36
; 4) a) 0,046; b) 0,028;
5) a)
1
9
, b)
2
9
, c)
3
9
; d)
2
9
, e)
1
9
;
6) 0,236; 7) 0,504.
2. п. 2.3.
1)
7
15
;
2)
1
5
;
3) 0,75; 4) 0,32; 5) 0,9955; 6)
7
12
.
2. п. 2.4.
1)
0,25; 2)
9
49
;
3) 0,467; 4) 0,6; 5) 0,5; 6)
1
6
;
7) 0,417.
2. п. 2.5.
1)
0,241; 2)
82 9 10
46 (1 ) 10 (1 ) (1 )
p
pppp⋅− + ⋅− +− ; 3) 0,657; 4) 0,041; 5) 0,525;
44
6) 5.
3. п. 3.1.
1)
5
5
(0,15) (0,85)()
ii i
x
xx
i
PX x C
−
== ;
i
x
0 1 2 3 4 5
i
p
0,44371 0,39150 0,13818 0,02439 0,00215 0,0007
2)
4
4
(0,05) (0,95)()
ii i
x
xx
i
P
Xx C
−
== ;
i
x
0 1 2 3 4
i
p
0,814506 0,171475 0,013538 0,000475 0,000006
3)
i
x
0 1 2 3
i
p
0,5
⋅ 0,7⋅ 0,7=
=0,245
0,5⋅ 0,7⋅ 0,7+
+0,5
⋅ 0,6⋅ 0,7+
+0,5
⋅ 0,7⋅ 0,3=
=0,455
0,5
⋅
0,3
⋅
0,3+
+0,5
⋅
0,3
⋅
0,7+
+0,5
⋅
0,7
⋅
0,3=
=0,255
0,5
⋅
0,3
⋅
0,3=
=0,045
4)
i
x
0 1 2 3 4
i
p
1
0, 2
5
=
41
0, 2
54
⋅=
431
0, 2
543
⋅⋅=
4321
0, 2
5432
⋅⋅⋅=
4321
10,
2
5432
⋅⋅⋅⋅=
5)
i
x
0 1 2 3
i
p
30
16 4
3
20
0,491228
CC
C
⋅
≈
≈
21
16 4
3
20
0,421052
CC
C
⋅
≈
≈
10
16 4
3
20
0,084211
CC
C
⋅
≈
≈
03
16 4
3
20
0,003509
CC
C
⋅
≈
≈
6)
i
x
0 1 2
i
p
0,2
⋅
0,1=0,02 0,8
⋅
0,1+0,9
⋅
0,2=
=0,26
0,8
⋅
0,9=0,72
3. п. 3.2.
1)
3
3
12
33
()
kk
k
PX k C
−
⎛⎞⎛⎞
⎜⎟⎜⎟
⎝⎠⎝⎠
== ; 0, 1, 2, 3k
=
,
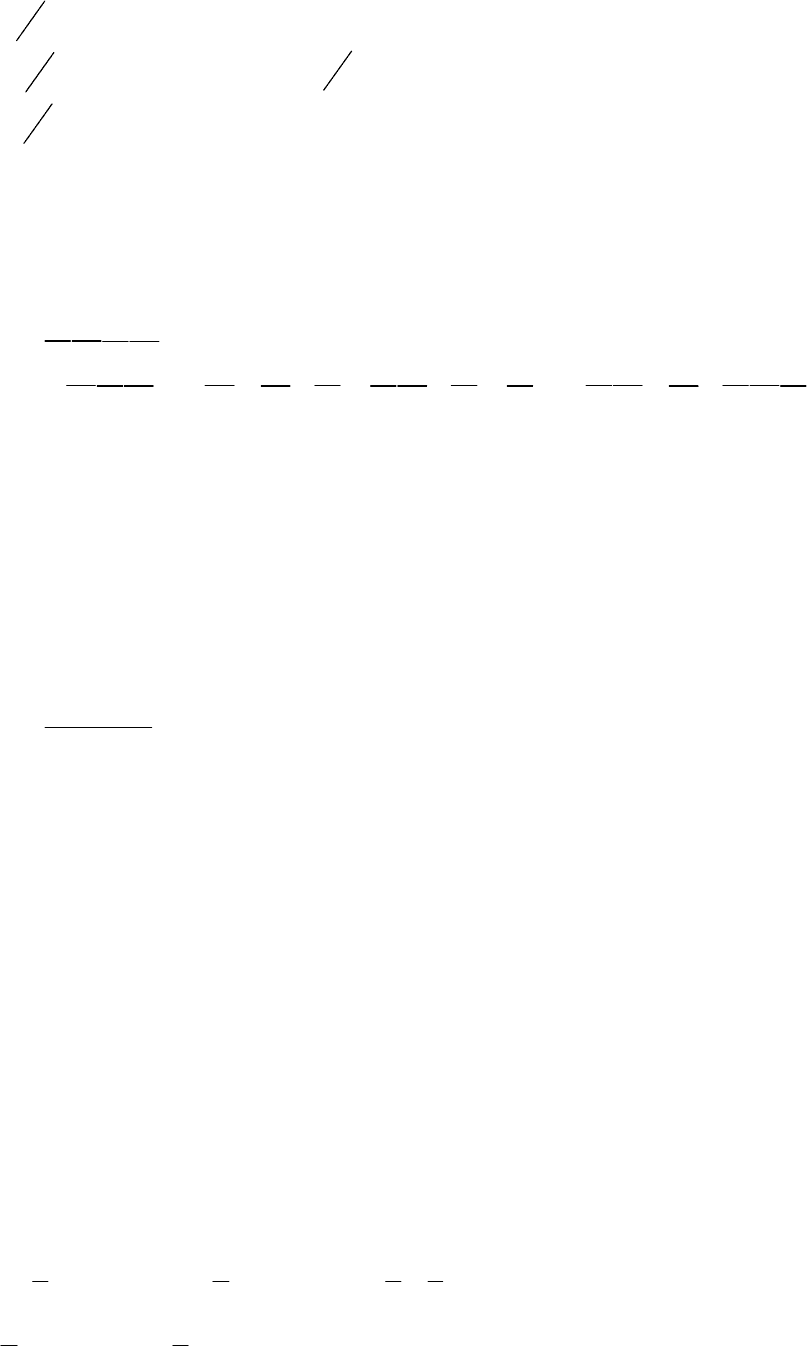
45
8
,0 1
27
7
26
,(2)
,1 2
27
27
26
,2 3
27
,3
0, 0
()
1
x
Px
x
x
x
x
Fx
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
<≤
≥=
<≤
<≤
<
≤
=
2) Рассмотрим события:
1
A
={первая установка обнаружила первый объект},
2
A
={первая установка обнаружила второй объект},
1
B ={вторая установка
обнаружила первый объект},
2
B ={вторая установка обнаружила второй
объект}.
1212
0,3 0,3 0,2 0,2 0,0036(0)( )PX PAABB =⋅⋅⋅=== ,
1212 1212 1212 1212 1212 1212
2 (0,7 0,3 0, 2 0, 2) 2 (0,3 0,3 0,8 0, 2) 2 (0, 7 0,3 0,8 0, 2) 0,1128
(1)( )P X P AABB AABB AABB AABB AABB AABB+++++ =
=⋅ ⋅⋅⋅ +⋅ ⋅⋅⋅ +⋅ ⋅⋅⋅ =
==
0,8836(2)1(0)(1)
P
XPXPX
=
==− =− =
0, 0
0,0036, 0 1
0,1164, 1 2
1, 2
()
x
x
x
x
Fx
⎧
⎪
⎪
⎨
⎪
⎪
⎩
≤
<≤
<≤
<
= , ( 1) 0,9964PX≥=
3)
4
5
15
4
20
()
kk
CC
PX k
C
−
⋅
== ,
0, 0
0,001032, 0 1
0,03199,
12
0,248709, 2 3
0,718266, 3 4
1, 4
()
x
x
x
x
x
x
Fx
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
≤
<
≤
<≤
<
≤
<
≤
<
=
, ( 3) 0,751291PX≥=
4) (0)0,7PX== , ( 1) 0,3 0,7 0,21PX== ⋅ = ,
( 2) 0,3 0,3 0, 7 0, 063PX== ⋅ ⋅ = , ( 3) 0,3 0,3 0,3 0,027PX
=
=⋅⋅=
0, 0
0,7, 0 1
0,91, 1 2
0,973, 2 3
1, 3
()
x
x
x
x
x
Fx
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
≤
<≤
<≤
<≤
<
= , ( 2) 0,19PX>=
5)
1
(2)
9
PX= = ,
2
(3)
9
PX= = ,
31
(4)
93
PX
=
==,
2
(5)
9
PX= = ,
1
(6)
9
PX==,
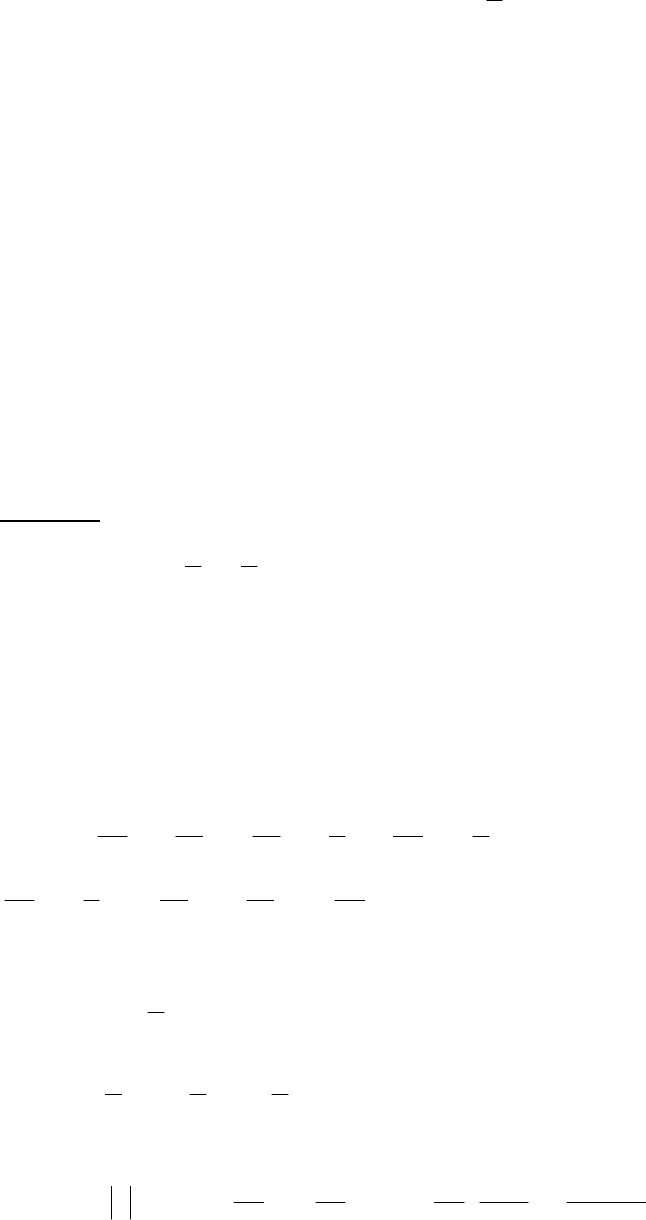
46
1/9
1/3
2/3
8/9
2
0,
23
,
,
34
,
45
,
56
1,
6
()
x
x
x
x
x
x
Fx
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
≤
<≤
<≤
<≤
<≤
<
=
,
5
(2 5)
9
PX
≤
≤=
6) 0,1 0,1 0,1 0,001(0)
P
X ⋅⋅=== ,
1
3
0,1 0,9 0,1 0,027(1)
P
XC⋅⋅=== ,
2
3
0,1 0,9 0,9 0, 243(2)
P
XC⋅⋅=== ,
0,9 0,9 0,9 0,729
(3)
P
X ⋅⋅=== .
0, 0
0,001, 0 1
0,028, 1 2
0, 271, 2 3
1, 3
()
x
x
x
x
x
Fx
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
≤
<≤
<≤
<≤
<
=
, (1 2) 0,27PX
≤
≤=
3. п. 3.3.
1)
3
3
15
66
()
k
k
k
PX k C
−
⎛⎞
⎛⎞
⎜⎟
⎜⎟
⎝⎠
⎝⎠
==
0 0,5787 1 0,3472 2 0,0695 3 0,0046 0,5
M
X ≈⋅ +⋅ +⋅ +⋅ =
2
0,6666
M
X ≈ , 0,4166DX ≈ .
2)
()()
5
5
0,8 0, 2()
kk
k
PX k C
−
==
0 0,00032 1 0,0064 2 0,0512 3 0,2048 4 0,4096 5 0,32768 4
M
X ≈⋅ +⋅ +⋅ +⋅ +⋅ +⋅ =
2
16,8
M
X ≈ , 0,8DX ≈ .
3) 6
111151
2345 7
36 18 12 9 36 6
MX ≈⋅ +⋅ +⋅ +⋅+⋅ +⋅+
51 1 1 1
8 9 10 11 12 7
36 9 12 18 36
+⋅ +⋅+⋅+⋅+⋅ =
2
54,833
M
X ≈
, 5,833DX ≈ .
4)
1
1
2
()
k
PX k
+
⎛⎞
⎜⎟
⎝⎠
==
11
00
111
242
kk
kk
kkMX
+
−
∞∞
==
⎛⎞ ⎛⎞
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
==
∑∑
Вычислим сумму ряда
()
()
()
1
2
000
11
1
1
1
k
kk
kkk
dd d
kx x x x
dx dx dx x
x
∞∞∞
−
===
⎛⎞
⎜⎟
⎝⎠
=<= = = =
−
−
∑∑∑
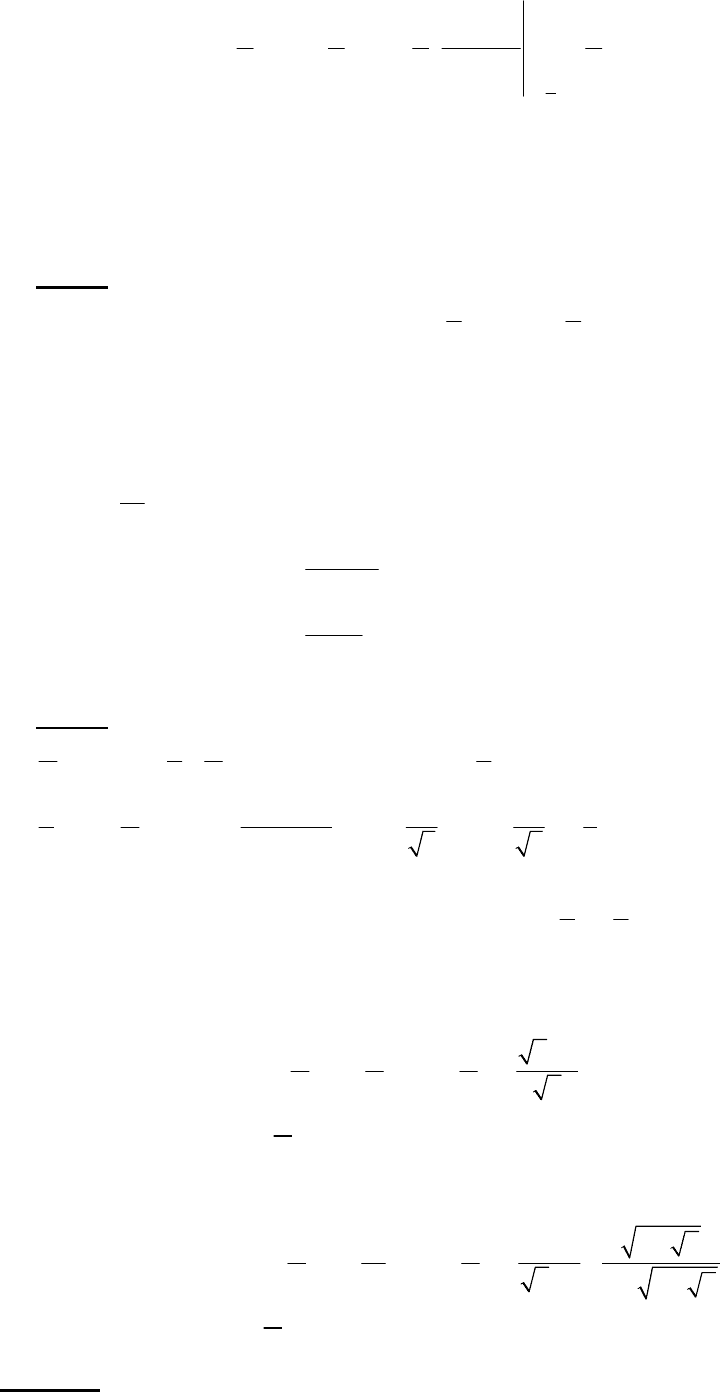
47
Следовательно,
()
1
2
0
1
2
1111 1
41
424 4
1
k
k
x
k
x
MX
−
∞
=
=
⎛⎞
⎜⎟
⎝⎠
⋅
=⋅ =⋅=
−
=
∑
5) 1 0,1 2 0,2 3 0,3 4 0,4 3
M
X =⋅ + ⋅ +⋅ + ⋅ = ,
2
10
M
X
=
, 1DX =
6) 0,504(3)PX== , 0,398(2)PX== , 0,092(1)PX
=
= , 0,006(0)PX== ,
2, 4
M
X =
,
2
6, 22MX = ,
0, 46DX
=
,
0,678X
σ
=
.
3. п. 3.4.
1)
()
0,5 0,1, 2,...,()
nk
n
knPX k C === ,
2
n
MX
=
,
4
n
DX
=
.
2) По биномиальному.
()()( )
10
10
0,9 0,1 0,1,...,10()
kk
k
kPX k C
−
⋅⋅ === , 9
M
X
=
,
0,9DX = .
3) Да, 6
M
X = , 2,4DX = , 1,55X
σ
=
.
4)
5
4
4
0,1563
5!
(5) ePX
−
≈== .
5)
0
0,25
(0, 25)
0,2212
0!
( 1)1 ( 0)1 ePX PX
−
≈≥=− = =−
6)
0
0,1
(0,1)
0,0952
0!
( 1)1 ( 0)1 ePX PX
−
≈≥=− = =−
4. п. 4.1.
1)
1
A
π
=
,
11
2
() arctgxFx
π
+=
,
1
4
(0 1)PX
<
<=
.
2)
1
2
A =
,
1
B
π
=
,
2
2
(4 )
()
x
fx
π
+
= ,
221
3
33
PX
⎛⎞
⎜⎟
⎝⎠
−
<< =.
3) 0
A
= ,
1
B
=
, 1C = ,
0, 0
1, 0 1
0, 1
()
x
x
x
fx
<
⎧
⎪
≤
≤
⎨
⎪
>
⎩
=
,
11
0
22
PX
⎛⎞
⎜⎟
⎝⎠
<
<=.
4) 1
A
= ,
0, 0
cos , 0
2
0,
2
()
x
xx
x
fx
π
π
⎧
⎪
≤
⎪
⎪
<≤
⎨
⎪
⎪
>
⎪
⎩
= ,
21
42
2
PX
ππ
−
⎛⎞
⎜⎟
⎝⎠
<< = .
5) 1
A
= ,
0, 0
,0
4
1,
2
()
x
tgx x
x
Fx
π
π
⎧
⎪
≤
⎪
⎪
<<
⎨
⎪
⎪
≥
⎪
⎩
= ,
122
16 8
21
222
PX
ππ
−
⎛⎞
−
⎜⎟
+
⎝⎠
++
<< = .
4. п. 4.2.
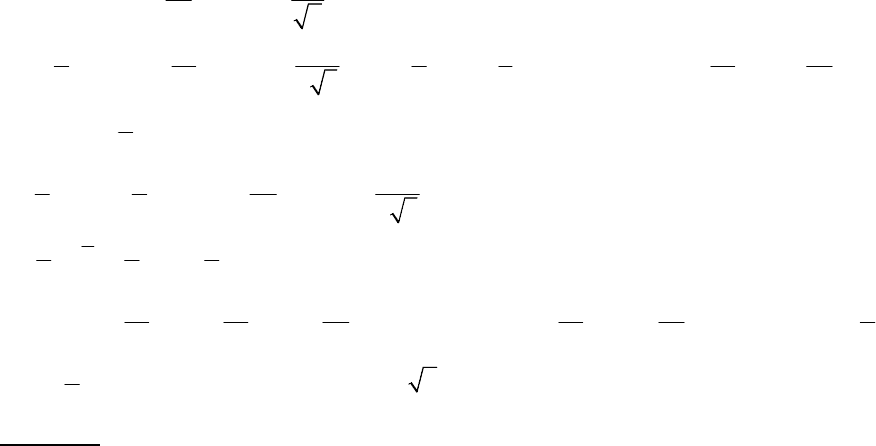
48
1) 0
X
m = ,
2
[]
6
a
DX
=
,. []
6
a
X
σ
= ,
3
0
μ
=
.
2)
1
2
X
m = ,
1
[]
12
DX
=
,.
1
[]
23
X
σ
= ,
3
1
4
α
=
,
4
1
5
α
=
,
13
0
μ
μ
=
=
,
2
1
12
μ
= ,
4
1
80
μ
= ,
0
X
S = ,
6
5
X
E =− .
3)
2
9
λ
= ,
3
2
X
m = ,
9
[]
20
DX = ,.
3
[]
25
X
σ
= .
4)
2
3
α
= ,
3
2
M = ,
3
2
μ
= .
5)
1
1
α
= ,
2
11
10
α
=
,
3
13
10
α
=
,.
4
57
35
α
=
,
13
0
μ
μ
=
=
,
2
1
10
μ
=
,
4
1
35
μ
=
, 0
X
S = ,
1
7
X
E
=
−
.
6)
3
2
X
E =− , 0
X
m
=
, [] 32DX = , [] 42X
σ
=
.
4. п. 4.3.
1)
(2 4) 0,023PX<<=
. 2)
(0 6) 0,698PX
<
<
=
,
( 2 2) 0,067PX
−
<<
=
. 3) 332
ε
=
.
4) 0, 95P = .
Литература
1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969.
2. Сборник задач по теории вероятностей, математической статистике и
теории случайных функций. / Под ред. А.А. Свешникова. – М.: Наука, 1970.

49
Приложение.
Приближенные значения функции стандартного нормального распределения
2
*
2
1
2
()
x
t
edtФ x
π
−
−∞
=
∫
, умноженные на
5
10
.
**
()1 ()Ф x Ф x
−
=−
.
X 0 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
50000
53983
57926
61791
65542
69146
72575
75804
78814
81594
84134
86433
88493
90320
91924
93319
94520
95543
96407
97128
97725
98214
98610
98928
99180
99379
99534
99653
99744
99813
99865
99903
99931
99952
99966
99977
99984
99989
99993
99995
50399
54380
58317
62172
65910
69497
72907
76115
79103
81859
84375
86650
88686
90490
92073
93448
94630
95637
96485
97193
97778
98257
98645
98956
99202
99396
99547
99664
99752
99819
99869
99906
99934
99953
99968
99978
99985
99990
99993
99995
50798
54776
58706
62552
66279
69847
73237
76424
79389
82121
84614
86864
88877
90658
92220
93574
94738
95728
96562
97257
97831
98300
98679
98983
99224
99413
99560
99674
99760
99825
99874
99910
99936
99955
99969
99978
99985
99990
99993
99996
51197
55172
59095
62930
66640
70194
73565
76730
79673
82381
84849
87076
89065
90824
92364
93699
94845
95818
96638
97320
97882
98341
98713
99010
99245
99430
99573
99683
99767
99831
99878
99913
99938
99957
99970
99979
99986
99990
99994
99996
51595
55567
59483
63307
67003
70540
73891
77035
79955
82639
85083
87286
89251
90988
92507
93822
94950
95907
96712
97381
97932
98382
98745
99036
99266
99446
99585
99693
99774
99836
99882
99916
99940
99958
99971
99980
99986
99991
99994
99996
51994
55962
59871
63683
67364
70884
74215
77337
80234
82894
85314
87493
89435
91149
92647
93943
95053
95994
96784
97441
97982
98422
98778
99061
99286
99461
99598
99702
99781
99841
99886
99918
99942
99960
99972
99981
99987
99991
99994
99996
52392
56356
60257
64058
67724
71226
74537
77637
80511
83147
85543
87698
89617
91308
92785
94062
95154
96080
96856
97500
98030
98461
98809
99086
99305
99477
99609
99711
99788
99846
99889
99921
99944
99961
99973
99981
99987
99992
99994
99996
52790
56749
60642
64431
68082
71566
74857
77935
80785
83398
85769
87900
89796
91466
92922
94179
95254
96164
96926
97558
98077
98500
98840
99111
99324
99492
99621
99720
99795
99851
99893
99924
99946
99962
99974
99982
99988
99992
99995
99996
53188
57142
61026
64803
68439
71904
75175
78230
81057
83646
85993
88100
89973
91621
93056
94295
95352
96246
96995
97615
98124
98537
98870
99134
99343
99506
99632
99728
99801
99856
99896
99926
99948
99964
99975
99983
99988
99992
99995
99997
53586
57535
61409
65173
68793
72240
75490
78524
81327
83891
86214
88298
90147
91774
93189
94408
95449
96327
97062
97670
98169
98574
98899
99158
99361
99520
99643
99736
99807
99861
99900
99929
99950
99965
99976
99983
99989
99992
99995
99997
50
Содержание
1. Непосредственное вычисление вероятностей ............................................. 3
1.1. Основные понятия. ....................................................................................... 3
1.2. Схема случаев ............................................................................................... 5
1.3. Геометрические вероятности ....................................................................... 9
2. Вероятности сложных событий .................................................................... 11
2.1. Действия с событиями ................................................................................ 11
2.2. Вероятность суммы и произведения событий ......................................... 15
2.3. Формула полной вероятности ................................................................... 18
2.4. Формула Байеса .......................................................................................... 19
2.5. Формула Бернулли ...................................................................................... 21
3. Дискретные случайные величины .............................................................. 22
3.1. Аналитический и табличный способы задания закона распределения 22
3.2. Функция распределения ............................................................................. 25
3.3. Математическое ожидании и дисперсия дискретной случайной
величины ............................................................................................................. 27
3.4. Биномиальное распределение и распределение Пуассона ..................... 29
4. Непрерывные случайные величины........................................................... 32
4.1. Плотность вероятности и функция распределения непрерывных
случайных величин ............................................................................................ 32
4.2. Моменты и числовые характеристики непрерывных случайных
величин ............................................................................................................... 35
4.3. Нормальный закон распределения ............................................................ 38
Ответы ................................................................................................................... 42
Литература............................................................................................................ 48
Приложение. ......................................................................................................... 49
