Блинова И.В., Попов И.Ю. Случайные события, случайные величины
Подождите немного. Документ загружается.


31
Значения X :
3 4 5
Вероятности
p
:
32
3
5
12
0,165
33
C
⎛⎞⎛⎞
⎜⎟⎜⎟
⎝⎠⎝⎠
≈
41
4
5
12
0,041
33
C
⎛⎞⎛⎞
⎜⎟⎜⎟
⎝⎠⎝⎠
≈
50
5
5
12
0,004
33
C
⎛⎞⎛⎞
⎜⎟⎜⎟
⎝⎠⎝⎠
≈
Пользуясь формулами (3.10), находим
M
X
⎡
⎤
⎣
⎦
, DX
⎡
⎤
⎣
⎦
и X
σ
⎡⎤
⎣⎦
:
1
1,667
3
5MX np
⎡⎤
⎣⎦
≈==⋅
,
12
51,111
33
DX
npq
⎡⎤
⎣⎦
==⋅⋅≈
,
1,054XXD
σ
⎡⎤
⎡⎤
⎣⎦
⎣⎦
≈= .
Пример 2. Частота вспышек средней мощности нестационарной звезды
составляет в среднем 10 вспышек в сутки. Какова вероятность того, что в
течение минуты будет зафиксировано
a) ровно две вспышки, b) не более двух вспышек?
Так как общее число вспышек в сутки равно 10, то математическое
ожидание
a их числа, приходящего на интервал времени длительностью в
одну минуту, будет
10
0,0069
24 60
a ≈
⋅
= . Вероятность того, что какая-то одна
вспышка произойдет в данную минуту мала. Именно
1
0,00069
24 60
p ≈
⋅
= .
Ввиду того, что вспышки взаимно независимы, случайное число
X вспышек,
происходящих в данную минуту, можно считать распределенным по закону
Пуассона. Тогда
22
0,0069
0,0069 1
0,000024
2! 2
(2)
a
e
e
a
PX
−
≈⋅≈== ;
012
2
0! 1! 2!
1
2
0,99913
( 2) ( 0) ( 1) ( 2)
aa a
a
aaa
ee e
a
a
e
PX PX PX PX
−− −
+
+=
++
=≈
≤= =+ =+ ==
Задачи.
1. Подбрасывание монеты производится n раз. Определить закон
распределения числа выпавших гербов. Найти математическое ожидание
и дисперсию этой случайной величины.
2. Хоккеист, исполняя штрафной бросок, забрасывает шайбу с вероятностью
0,9. По какому закону распределено число заброшенных шайб при 10
бросках? Каково среднее число заброшенных шайб и какова дисперсия
этой случайной величины?
3. Игра заключается в набрасывании колец на колышек. Игрок получает 10
колец и последовательно набрасывает их на колышек, причем вероятность
удачной попытки равна 0,4 при каждом броске. Можно ли утверждать, что

32
число X промахов игрока распределено по биномиальному закону?
Найти
M
X
⎡⎤
⎣⎦
, DX
⎡⎤
⎣⎦
и X
σ
⎡
⎤
⎣
⎦
.
4. Автоматическая телефонная станция получает в среднем 240 вызовов в
час. Какова вероятность того, что в данную минуту она получит пять
вызовов?
5. При контроле выпускаемых деталей автоматический контроллер
отбраковывает в среднем 15 деталей в час. Считая, что число
забракованных деталей распределено по закону Пуассона, найти
вероятность того, что в данную минуту будет забракована хотя бы одна
деталь.
6. Среднее число отказов при передаче сигнала радиорелейной станции
равно 20 за 4800 часов работы. Определить вероятность хотя бы одного
отказа станции в течение суток.
4. Непрерывные случайные величины
4.1. Плотность вероятности и функция распределения
непрерывных случайных величин
Плотностью распределения вероятностей или, просто, плотностью
вероятности непрерывной случайной величины
X называется предел
отношения вероятности попадания случайной величины в интервал
()
,
x
xx+Δ к
x
Δ при стягивании этого интервала к точке
x
.
0
()
() lim
x
Px X x x
x
fx
Δ→
<
<+Δ
Δ
= (4.1)
Отсюда следует, что произведение
()
f
xx
⋅
Δ с точностью до бесконечно
малых высшего порядка относительно
x
Δ
равно вероятности попадания
случайной величины
X в интервал
(
)
,
x
xx
+
Δ .
Если плотность вероятности известна, то вероятность попадания
непрерывной случайной величины в интервал
(
)
,ab находится по формуле
()()
b
a
f
xdxPa X b<<=
∫
(4.2)
Существует следующая связь между плотностью вероятности и функцией
распределения непрерывной случайной величины:
() '()
f
xFx= ; () ()
x
Fx ftdt
−
∞
=
∫
(4.3)
График плотности вероятности называется кривой распределения
случайной величины
X . Примерный вид кривой распределения и графика
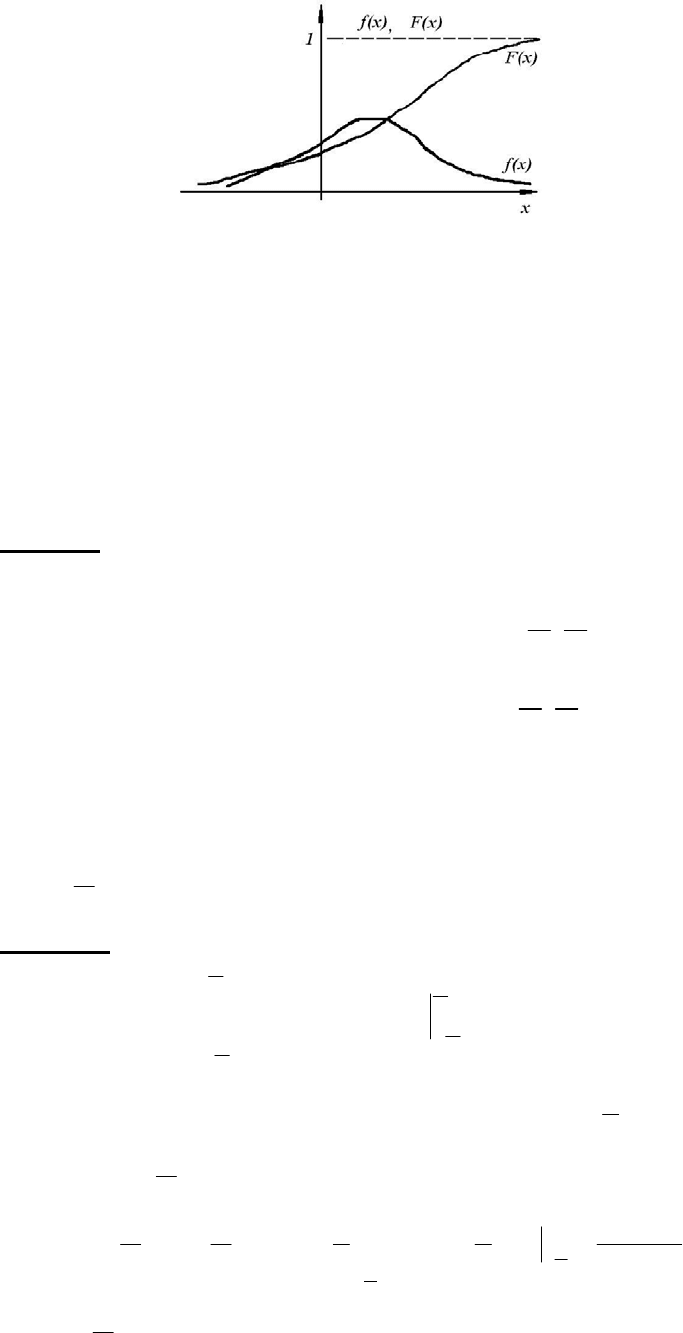
33
функции распределения непрерывной случайной величины показан на
рис.11.
Рис. 11.
Основные свойства плотности вероятностей:
1.
() 0
f
x ≥ ,
2.
1()
f
xdx
+∞
−∞
=
∫
.
Всякая функция
()
f
x
, удовлетворяющая этим свойствам, может
рассматриваться как плотность вероятности некоторой непрерывной
случайной величины.
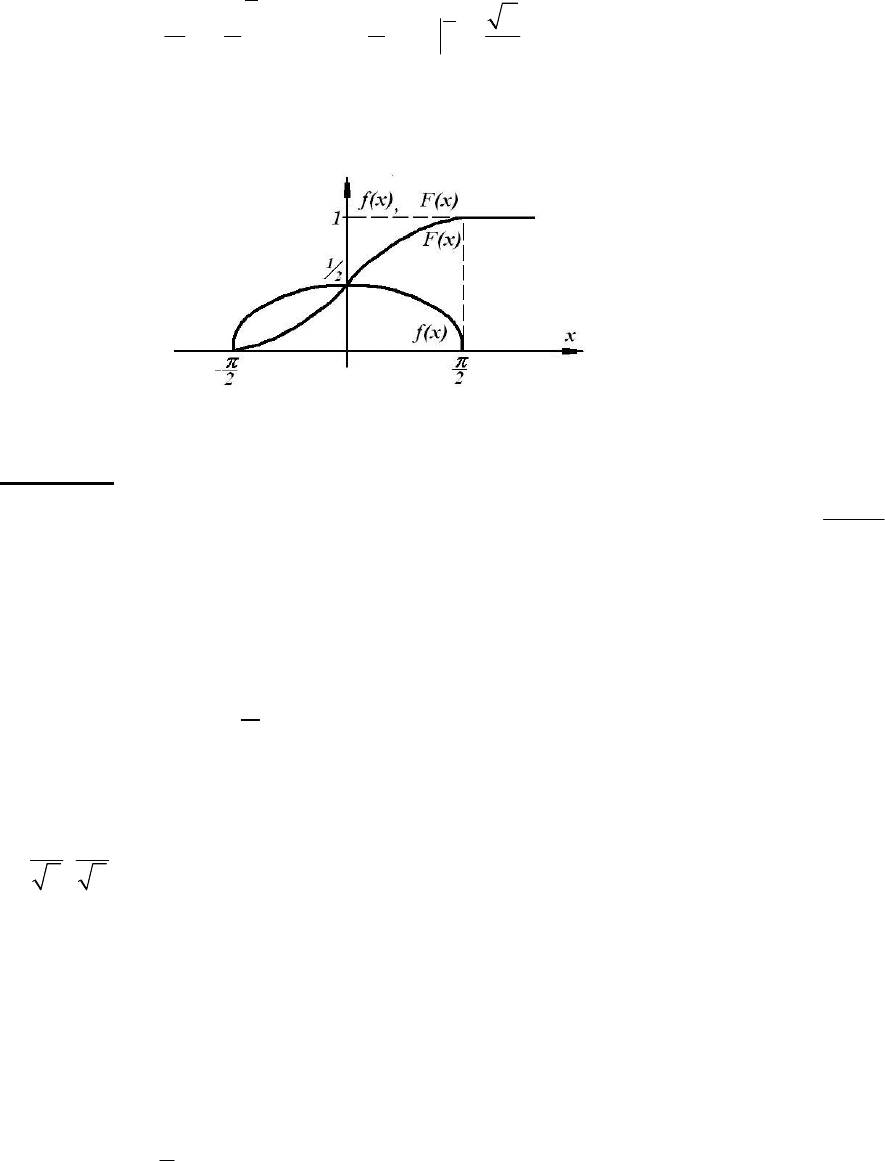
Пример. Пусть плотность вероятности случайной величины X задана
следующим образом:
cos , ,
22
()
0, ,
22
axесли x
fx
если x
π
π
π
π
⎧
⎛⎞
⎪
⎜⎟
⎪
⎝⎠
⎨
⎛⎞
⎪
⎜⎟
⎪
⎝⎠
⎩
∈−
=
∉−
a)
Найти значение постоянной a .
b)
Найти функция распределения случайной величины X .
c)
Найти вероятность попадания случайной величины X в интервал
0,
4
π
⎛⎞
⎜⎟
⎝⎠
.
Решение.
a)
2
2
2
2
() cos sin 2
f
xdx a xdx a x a
π
π
π
π
+∞
−
−∞
−
===
∫∫
В соответствии со свойствами (2)
21a
=
, отсюда
2
1
a
=
.
b)
При ,
2
() 0xFx
π
≤− = ,
при
2
2
111sin
,() cos sin
22 2 2 2
x
x
x
Fx tdt tx
π
π
ππ
−
−
+
<===
−<
∫
,
при
,()1
2
Fxx
π
=≤ .
34
c)
4
4
0
0
112
cos sin
42 2 4
(0 ) xdx xPX
π
π
π
==<< =
∫
.
Кривая распределения и график функции распределения приведены на
рис. 12.
Рис. 12
Задачи.
1. Случайная величина X имеет плотность вероятности
2
1
()
A
x
fx
+
= .
Определить постоянную
A
. Найти функция распределения
()Fx
и
вычислить вероятность попадания случайной величины
X в интервал
(0,1).
2. Функция распределения случайной величины X имеет вид
2
()
x
Fx A Barctg=+⋅ (закон Коши). Определить постоянные
A
и B , и
плотность вероятности
()
f
x
. Построить графики
()
f
x
и
()Fx
.
Определить вероятность попадания случайной величины
X в интервал
22
,
33
⎛⎞
⎜⎟
⎝⎠
−
.
3. Закон распределения случайной величины X определен формулой
,0
() ,0 1
,1
Ax
Fx Bx x
Cx
⎧
⎪
⎨
⎪
⎩
<
=
≤≤
>
Найти значения параметров
А, В и С, плотность вероятности ()
f
x .
Вычислить вероятность того, что случайная величина
X будет лежать в
интервале
1
0,
2
⎛⎞
⎜⎟
⎝⎠
.
4. Функция распределения случайной величины X задана выражением
35
0, 0
() sin,0
2
1,
2
x
Fx A x x
x
π
π
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
≤
=
<≤
>
Найти коэффициент
А и плотность функции распределения ()
f
x этой
случайной величины. Найти вероятность попадания случайной величины
X в интервал ,
42
π
π
⎛⎞
⎜⎟
⎝⎠
.
5. Плотность вероятности случайной величины X имеет вид
2
0, 0
() ,0
4
cos
0,
4
x
A
fx x
x
x
π
π
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
≤
=
<<
≥
Определить постоянную
А и функцию распределения ()Fx случайной
величины
X . Найти вероятность того, что случайная величина X
принимает значение в интервале
,
16 8
π
π
⎛⎞
⎜⎟
⎝⎠
.
4.2. Моменты и числовые характеристики непрерывных
случайных величин
Начальным моментом порядка r случайной величины X называется
величина, которая определяется выражением
()
r
r
Xxfxdx
α
+
∞
−
∞
⎡⎤
⎣⎦
=
∫
(4.4)
Центральным моментом порядка
s
случайной величины X называется
величина, которая определяется выражением
()()
s
s
X
Xxmfxdx
μ
+
∞
−
∞
⎡⎤
⎣⎦
= −
∫
(4.5)
В этих формулах
()
f
x
- плотность вероятности,
X
m - математическое
ожидание случайной величины
X .
Центральные моменты можно выразить через начальные моменты,
например,
2
221
α
α
μ
=
−
3
33 21 1
32
α
αα α
μ
=
−+ (4.6)
36
Математическим ожидаем
M
X
⎡
⎤
⎣
⎦
или
X
m случайной величины X
называется ее начальный момент первого порядка
1
M
XX
α
⎡
⎤⎡⎤
⎣
⎦⎣⎦
= , то есть
()
M
Xxfxdx
+
∞
−
∞
⎡⎤
⎣⎦
=
∫
(4.7)
Дисперсией случайной величины
X называется ее центральный момент
второго порядка
2
DX X
μ
⎡⎤ ⎡⎤
⎣⎦ ⎣⎦
= , или
2
()()
X
DX x m fxdx
+
∞
−
∞
⎡⎤
⎣⎦
= −
∫
(4.8)
Основные свойства математического ожидания и дисперсии указаны в
пункте 3.3.
Символ математического ожидания может использоваться для
обозначения начальных и центральных моментов любого порядка, так
r
r
XMX
α
⎡
⎤⎡⎤
⎣
⎦⎣⎦
= ,
()
s
s
X
mXMX
μ
⎡
⎤
⎡⎤
⎢
⎥
⎣⎦
⎣
⎦
= − (4.9)
В качестве числовых характеристик случайных величин могут
использоваться моменты более высокого порядка. Наиболее
употребительными являются:
- коэффициент асимметрии
3
3
X
X
s
μ
σ
= , характеризующий
несимметричность кривой распределения относительно вертикальной
прямой, проходящей через точку
X
m ;
- эксцесс
4
4
3
X
X
E
μ
σ
=−, характеризующий отличие данного распределения
от нормального. Для нормального распределения (п. 4.3) эксцесс равен нулю.
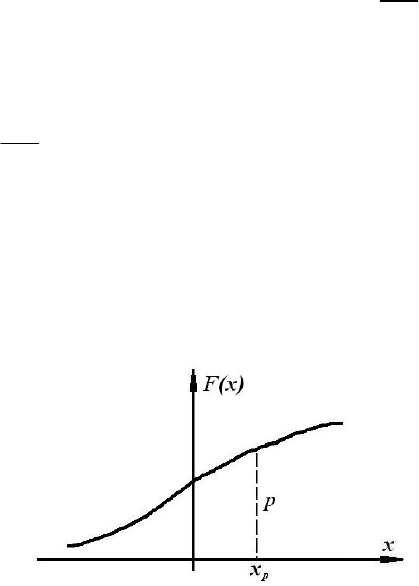
Квантилью порядка
p случайной величины X называется ее возможное
значение
p
x
, соответствующее значению функции распределения, равному
p (рис. 13).
Рис. 13.
Некоторые квантили имеют специальные названия:
a)
Медиана – квартиль
0,5
x
. Вероятность попадания случайной величины
X левее или правее этой точки одинакова и равна 0,5.
b)
Квартили – это квантили
0,25
x
и
0,75
x
и др.
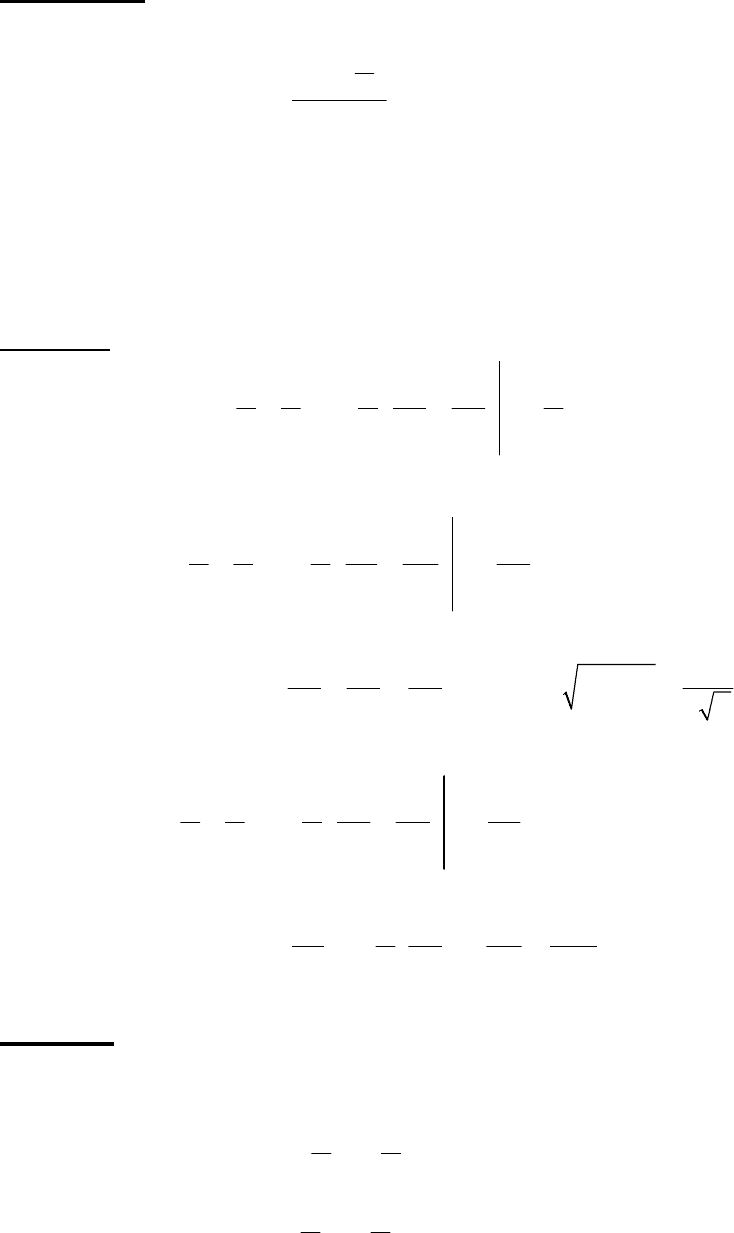
37
Пример 1. Случайная величина X распределена по «закону
прямоугольного треугольника» с плотностью вероятности
()
()
2(1 )
,0,
()
0, 0,
x
a
при x а
fx
a
при x а
⎧
⎪
⎪
⎨
⎪
⎪
⎩
−
∈
=
∉
Найти числовые характеристики случайной величины
X :
X
m , DX
⎡
⎤
⎣
⎦
,
X
σ
⎡⎤
⎣⎦
,
3
X
μ
⎡⎤
⎣⎦
.
Решение. По формуле (4.7) находим
23
1
0
0
12
21
23 3
X
a
a
x
xx a
mx dx
aa a
a
α
⎛⎞
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
==⋅ −⋅ = − =
∫
.
Для нахождения
DX
⎡⎤
⎣⎦
определим начальный момент
2
α
:
34 2
2
2
0
0
12
21
34 6
a
a
x
xx a
xdx
aa a
a
α
⎛⎞
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
=⋅−⋅= − =
∫
Пользуясь формулой (4.6) находим
22 2
2
221
6918
aaa
DX
μαα
⎡⎤
⎣⎦
==−=−=,
32
a
XDX
σ
⎡⎤ ⎡⎤
⎣⎦ ⎣⎦
==.
Определим начальный момент
3
α
3
45 3
3
0
0
12
21
5
410
a
a
x
xx a
xdx
aa a a
α
⎛⎞
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
= ⋅−⋅ = − =
∫
Пользуясь формулой 4.6, находим
3
3233
3
312 1
32 3 2
10 3 6 27 135
aaaaa
μα αα α
=− + =−⋅⋅+ =
.
Задачи.
1. Случайная величина X распределена по закону Симпсона («закону
равнобедренного треугольника») с плотностью вероятности
1
1, 0
1
() 1 , 0
0,
x
при xa
aa
x
fx при ax
aa
при xaили xa
⎧
⎛⎞
⎪
⎜⎟
⎪
⎝⎠
⎪
⎛⎞
⎪
⎨
⎜⎟
⎝⎠
⎪
⎪
⎪
⎪
⎩
−
<<
=+ −<≤
≤
−≥
38
Определить следующие числовые характеристики случайной величины
X :
X
m , DX
⎡⎤
⎣⎦
, X
σ
⎡⎤
⎣⎦
,
3
μ
.
2. Определить числовые характеристики равномерно распределенной
случайной величины
X (задача 3, п. 4.1).
3. Дана функция
2
0, 0
() (3 ),0 3
0, 3
x
f
xxxx
x
λ
⎧
⎪
⎪
⎨
⎪
⎪
⎩
<
=−≤≤
>
При каком
λ
функция ()
f
x может быть принята за плотность
вероятности случайной величины
X ? Определить
M
X
⎡⎤
⎣⎦
, DX
⎡
⎤
⎣
⎦
и
X
σ
⎡⎤
⎣⎦
этой случайной величины.
4. Дана плотность вероятности случайной величины X
2
0, 0
() ( ),0 3
3
0, 3
x
x
f
xx x
x
α
⎧
⎪
⎪
⎨
⎪
⎪
⎩
<
=
−≤≤
>
Определить постоянную
α
. Найти моду
M
и медиану
μ
этой случайной
величины.
5. Плотность распределения случайной величины X определена формулой
2
2
0, 0
3
,0 1
2
()
3(2 )
,1 2
2
0, 2
x
x
x
fx
x
x
x
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
<
≤
<
=
−
≤
<
>
Определить начальные и центральные моменты первых четырех порядков,
асимметрию и эксцесс этой случайной величины.
6. Найти эксцесс случайной величины X , распределенной по
экспоненциальному закону с плотностью
2
()
x
f
xe
−
= . Определить ее
математическое ожидание, дисперсию и среднее квадратическое
отклонение.
4.3. Нормальный закон распределения
Нормальный закон распределения имеет особое значение. Если случайная
величина
X зависит от большого числа примерно одинаково влияющих на
нее факторов, то в большинстве случаев это приводит к нормальному
39
распределению случайной величины. Кроме того, нормальное распределение
является предельным по отношению к некоторым другим распределениям.
Нормальное распределение случайной величины
X задается плотностью:
2
2
()
2
1
2
()
X
X
xm
X
efx
σ
σπ
−
⋅=
(4.10)
здесь
X
m - математическое ожидание случайной величины,
2
X
σ
- ее
дисперсия.
Кривая нормального распределения симметрична относительно
вертикальной прямой, проходящей через точку
X
m . Медиана нормального
распределения совпадает с математическим ожиданием. Коэффициент
асимметрии
X
s
и эксцесс
X
E равны нулю. Влияние
X
σ
на вид кривой
нормального распределения показано на рис. 14.
Рис. 14.
Функция распределения случайной величины
X , имеющей нормальное
распределение с параметрами
X
m и
X
σ
(
,()
XX
XNm
σ
∈
):
2
2
1
2
()
X
X
x
m
t
edtFx
σ
π
−
−
−∞
=
∫
(4.11)
Имеются таблицы значений (см. Приложение) функции распределения
нормированного нормального закона с параметрами 0
X
m = и 1
X
σ
= :
2
*
2
1
2
()
x
t
edtФ x
π
−
−∞
=
∫
(4.12)
а также таблицы значений функции Лапласа:
2
2
0
1
2
()
x
t
edtФ x
π
−
=
∫
(4.13)
Функция распределения нормированного нормального закона и функция
Лапласа связаны соотношением:
*
1
2
() ()Ф x Ф x
=
+
(4.14)
Функция распределения случайной величины
X , подчиненной
нормальному закону с параметрами
X
m и
X
σ
, выражается через функцию
распределения нормированного нормального закона следующим образом:
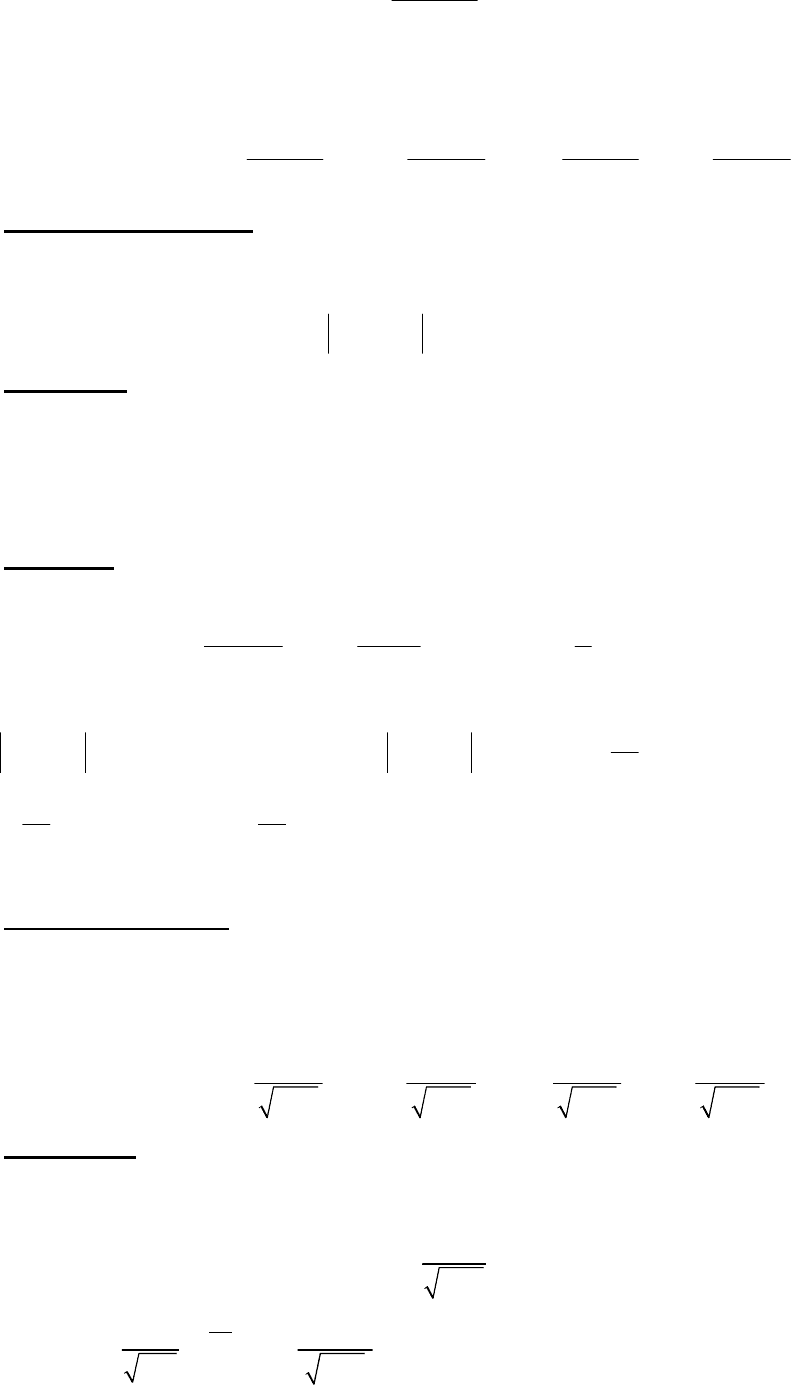
40
*
()
X
X
x
m
Fx Ф
σ
⎛⎞
⎜⎟
⎜⎟
⎝⎠
−
=
(4.15)
Вероятность попадания нормально распределенной случайной величины
X в интервал (,)ab находится по формуле:
**
()
XXXX
XXXX
bm am bm am
Pa X b ФФ ФФ
σσσσ
⎛⎞⎛⎞⎛⎞⎛⎞
⎜⎟⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟⎜⎟
⎝⎠⎝⎠⎝⎠⎝⎠
−−−−
−=−
<<= (4.16)
Правило трех сигм. Вероятность попадания нормально распределенной
случайной величины
X в интервал
(3,3)
XXXX
mm
σ
σ
−
+
близка к единице.
Точнее:
(
)
30,997
XX
mPX
σ
<− .
Пример 1. Случайная величина X распределена по нормальному закону
с математическим ожиданием 10
X
m
=
и дисперсией
2
100
X
σ
= . Найти
вероятность попадания случайной величины
X в интервал
520(, )
. Какую
точность отклонения
ε
случайной величины X от ее математического
ожидания можно гарантировать с вероятностью 0,9?
Решение. Среднее квадратическое отклонение 10
X
σ
= . Найдем,
используя таблицу значений функции Лапласа,
()
20 10 5 10 1
1 0,34 0,19 0,53
10 10 2
(5 20)PX ФФФФ
⎛⎞⎛⎞ ⎛⎞
⎜⎟⎜⎟ ⎜⎟
⎝⎠⎝⎠ ⎝⎠
−−
+=+ +=
<< =
.
Для определения гарантированной точности
ε
, при которой
(10)0,9PX
ε
−<≥ . Найдем
10
(10)2PX Ф
ε
ε
⎛⎞
⎜⎟
⎝⎠
−<= . Решая уравнение
0,9
10
2Ф
ε
⎛⎞
⎜⎟
⎝⎠
= , получим 1,645
10
ε
или 16,45
ε
. Ввиду того, что функция Ф
возрастает, в качестве
ε
можно взять
16,5
ε
=
.
Теорема Лапласа. Вероятность попадания в интервал (,)ab случайной
величины
X - числа наступления события
A
в n опытах, в каждом из
которых это событие может произойти с одной и той же вероятностью
p ,
при большом числе опытов приближенна равна:
**
()
bnp anp bnp anp
npq npq npq npq
Pa X b ФФ ФФ
⎛⎞⎛⎞⎛⎞⎛⎞
⎜⎟⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟⎜⎟
⎝⎠⎝⎠⎝⎠⎝⎠
−−−−
−=−
<<
(4.17)
Следствие. Если в каждом из n опытов событие
A
может произойти с
одинаковой вероятностью
p , то вероятность наступления события
A
в этих
опытах
m раз, при большом числе опытов приближенно равна
1
()
()
x
npq
PX m
ϕ
= , (4.18)
здесь
2
2
1
()
2
x
x
e
ϕ
π
−
= ,
mnp
npq
x
−
= ,
1qp
=
−
.
