Biringen S., Chow C.-Y. An Introduction to Computational Fluid Mechanics by Example

Подождите немного. Документ загружается.

182 VISCOUS FLUID FLOWS

The ﬂuid region is covered with a square mesh of size h having m horizontal

grid lines and an equal number of vertical grid lines, as shown schematically in

Fig. 3.7.1. Next, we derived expressions for boundary values of ζ in terms of ψ,

which are needed for solving (3.7.7).

Let us ﬁrst consider an arbitrary grid point (i, m) at the moving plate on top

of the cavity. Our purpose is to calculate the vorticity at this point based on the

local velocity and on the information of ψ at four neighboring grid points marked

in Fig. 3.7.1. Similar to expression (2.9.4), we now assume the following form

for vorticity at (i, m):

i,m

=−



∂

∂x

∂

∂y



i,m

= α

i−1,m−1

+α

i,m−1

+α

i+1,m−1

+α

i,m−2

+α



∂ψ

∂y



i,m

(3.7.14)

Substituting from the Taylor’s series expansions,

i±1,m−1

= ψ

i,m

±h



∂ψ

∂x



i,m



∂

∂x



i,m

−h



∂ψ

∂y



i,m



∂

∂y



i,m

+O(h

)

i,m−n

= ψ

i,m

−nh



∂ψ

∂y



i,m



∂

∂y



i,m

+O(h

)

and retaining only terms up to O(h

), (3.7.14) becomes

−



∂

∂x

∂

∂y



i,m

= (α

+α

)ψ

i,m

+(α

−α



∂ψ

∂x



i,m



−α

−2α





∂ψ

∂y



i,m

+(α

+α

)



∂

∂x



i,m

+(α

+α

+4α

)



∂

∂y



i,m

The constants α’s are determined by equating the coefﬁcients of like terms on

the two sides of this equation. Substitution of these values into (3.7.14) gives

i,m



−ψ

i−1,m−1

i,m−1

−ψ

i+1,m−1

−

i,m−2



−



∂ψ

∂y



i,m

(3.7.15)

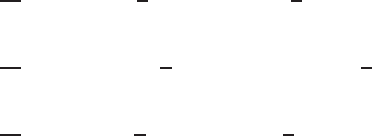
NUMERICAL SOLUTION OF BIHARMONIC EQUATIONS—STOKES FLOWS 183

where (∂ψ/∂y)

i,m

has the constant value of 1 according to the second boundary

condition in (3.7.13). By analogy we can write down the expressions for vorticity

at the three stationary boundaries as

1, j



−ψ

2, j −1

2, j

−ψ

2, j +1

−

3, j



(3.7.16)

m, j



−ψ

m−1, j −1

m−1, j

−ψ

m−1, j +1

−

m−2, j



(3.7.17)

i,1



−ψ

i−1,2

i,2

−ψ

i+1,2

−

i,3



(3.7.18)

in which the derivative boundary conditions in (3.7.10) to (3.7.12) have been

employed.

The vorticity boundary conditions just derived enable us to solve (3.7.7) pro-

vided ψ is known at some interior points. However, the determination of ψ from

(3.7.6) depends on the distribution of vorticity within the bounded domain. Thus,

ψ and ζ are coupled, and an iterative scheme will be constructed to ﬁnd the

solution.

A stationary state is ﬁrst assumed so that ψ = 0everywhereintheﬂuid

region. Based on this initial assumption, the boundary values computed from

(3.7.15) to (3.7.18) show that vorticity is initially generated at the moving plate.

This concentrated vorticity starts to diffuse into the cavity, resulting in a tempo-

rary vorticity distribution that is the solution of (3.7.7) that satisﬁes the present

boundary conditions. This computed vorticity distribution causes a modiﬁcation

to the assumed ψ after solving (3.7.6) subject to the restriction that ψ = 0on

the boundary. In this way we have completed the ﬁrst iteration. To start the next

iteration, the boundary values of vorticity are recomputed based on the modiﬁed

stream function, and the same procedure is repeated to obtain a new solution for

ψ and ζ . During each iteration the difference between the newly computed ζ

and the previous value at every grid point is recorded as the local error, and the

sum of absolute errors at all grid points is called

ERZETA. The same is done for

ψ, and the corresponding sum is called

ERPSI. Iteration is terminated when both

ERZETA and ERPSI are smaller than a speciﬁed small positive value EPSLON;the

solution at this stage is then considered to be satisfactory, since it has the desired

accuracy.

In Program 3.6 an iteration counter

ITER is introduced whose value is printed

only when the ﬁnal result has been obtained. The Poisson equation (3.7.6) is

solved by applying Liebmann’s iterative formula (2.8.6) repeatedly at all interior

points. The iteration method is programmed in a subroutine named

LIEBMN for

a square domain. The same subroutine is called to solve the Laplace equation

(3.7.7), which is, in fact, a Poisson equation with a vanishing right-hand side.

When Liebmann’s method is used, the values of vorticity at the corners

A, B, C ,andD of the cavity (Fig. 3.7.1) are not involved in the numerical

computation for solving equations (3.7.6) and (3.7.7). These values are computed

184 VISCOUS FLUID FLOWS

FIGURE 3.7.2 Stream function plot. +, PSI =−0.09;

◦

, PSI =−0.075; , PSI =−0.06; ♦,

PSI =−0.045; ∇, PSI =−0.03; , PSI =−0.015; ×, PSI = 0.

from the ﬁnal vorticity distribution by taking the average of the values at two

neighboring grid points.

After printing the numerical values ψ and ζ for the ﬁnal solution (Table 3.A.6)

the ﬂow pattern is plotted in Fig. 3.7.2. It turns out that the stream function is

either negative or zero in the present problem, so that the absolute value of ψ is

used instead in determination of the plotting symbols for various ranges of the

stream function.

The output of Program 3.6 shows that with

EPSLON = 0.001, 109 iterations

are needed to have the numerical result converge to the desired solution. During

the last iteration,

ERPSI, or the sum of absolute errors in the computation for ψ,

is 0.00004, whereas

ERZETA, the sum of absolute errors in the computation for

ζ , is 0.00094. After being distributed among 121 grid points, the average error

at each grid point is really a very small quantity.

The printed values of ψ show that stream function is symmetric about the

vertical line passing through the center of the cavity, but a slight asymmetry

in vorticity is detected at some locations. The errors, which appear only at the

third decimal place, can be reduced by assigning a number smaller than 0.001

ERRMAX when the subroutine LIEBMN is called. But to obtain a solution of

higher accuracy requires a longer computer time. Program 3.6 is constructed for

FLOW STABILITY AND PSEUDO-SPECTRAL METHODS 185

demonstration, and the accuracy of the result is not a main consideration here.

On the other hand, results of higher resolutions can be obtained by increasing

the total number of grid points.

Problem 3.13 Solve for the Stokes ﬂow in the square cavity shown in Fig. 3.7.1

with a free surface CD and a bottom surface AB moving at a constant unit velocity

in the positive x direction.

3.8 FLOW STABILITY AND PSEUDO-SPECTRAL METHODS

In this section, we consider two problems that serve as examples of ﬂow sta-

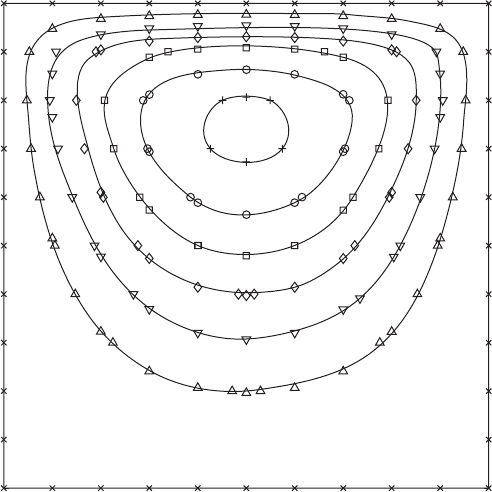
bility subject to different types of excitation. The ﬁrst is the Rayleigh-Benard

problem, in which a horizontal layer of ﬂuid heated from below becomes unsta-

ble due to buoyancy forces lifting the hot ﬂuid upward. Then, continuity requires

ﬂuid from the colder, upper region of the ﬂow to move downward, thus set-

ting up a pattern called Benard cells. A full account of this problem is offered

in Section 4.3. Here, we will simply consider the same problem introduced in

Section 4.3, but instead of solving the full nonlinear system, we will ﬁrst lin-

earize the governing equations, then apply separation of variables and convert

the governing partial differential equations into a system of ordinary differential

equations, and ﬁnally solve the resulting system using a MATLAB eigenvalue

solver. The solution of this system will provide the conditions under which an

otherwise quiescent horizontal layer of ﬂuid will become unstable with respect

to a certain scaling parameter of the system. Once a threshold value for this

parameter is exceeded, then the system becomes unstable and a convective ﬂow

pattern is established. The characteristic nondimensional number for this problem

is the Rayleigh number, deﬁned as

Ra =

gαTH

κν

(3.8.1)

Here, g is the gravitational acceleration, α is the thermal expansion coefﬁcient,

T is the temperature difference between the lower (hot) surface and the upper

(cold) surface, H is the height of the horizontal ﬂuid layer, κ is the thermal

diffusivity, and ν is the kinematic viscosity of the ﬂuid. From (3.8.1), it is appar-

ent that the Rayleigh number is the ratio, (buoyant energy production)/(energy

diffusion).

We adopt the Boussinesq approximation (Section 4.3), and write the governing

equations in the primitive variable form (see Section 4.5). For two-dimensional

incompressible ﬂows, the primitive variables of the problem are the velocity

components u, w and the pressure p. In the presence of surface heating, as

in the present problem, the energy equation must also be considered. Conse-

quently, for this problem, the fourth dependent variable is temperature, T .The

governing equations are the continuity equation, the x-momentum equation, the

z-momentum equation (in the vertical direction, by convention), and the energy

186 VISCOUS FLUID FLOWS

> T

FIGURE 3.8.1 Schematic of the Benard problem.

equation written with respect to Fig. 3.8.1, viz.,

∂u

∂x

∂w

∂z

= 0 (3.8.2)

∂u

∂t

∂u

∂x

∂u

∂z

=−

∂p

∂x

+Pr ∇

u (3.8.3)

∂w

∂t

∂w

∂x

∂w

∂z

=−

∂p

∂z

+Pr ∇

w + RaPr θ (3.8.4)

∂θ

∂t

∂θ

∂x

∂θ

∂z

=∇

θ (3.8.5)

In these equations, Pr is the Prandtl number expressing the the ratio (viscous

diffusion)/(thermal diffusion) and is given as Pr = ν/κ. These equations have

been nondimensionalized in the following manner:

u =

U , w =

W , x =

, z =

θ =

(T − T

)

−T

)

, p =

P, t =

(3.8.6)

In these expressions, U , W, X , Z , T , P,andτ are dimensional quantities, and ρ

is the reference ﬂuid density (Section 4.3). We now assume that the instabilities

due to buoyancy will have very small amplitudes, and the initial state of the

ﬂuid is quiescent so that the dependent variables can be separated into a mean

component that represents the initial conditions (base state), and a time-dependent

component that represents the perturbation ﬁeld,

u = 0 + ˆu(x, z, t)

w = 0 + ˆw(x, z , t)

p =

p(z) + ˆp(x, z , t)

θ =

θ(z) +

θ(x, z, t)

(3.8.7)

FLOW STABILITY AND PSEUDO-SPECTRAL METHODS 187

The base state is satisﬁed by

u = w = 0

ˆp = 0

θ = 0,

=−1

(3.8.8)

so that the z-momentum and energy equations for the base state become, respec-

tively,

∂

∂z

= RaPr

θ (3.8.9)

∂

∂t

=∇

θ (3.8.10)

Next, the governing equations (3.8.2)–(3.8.5) are linearized according to the

following script:

a. Substitute decomposed variables, (3.8.7), into (3.8.2)–(3.8.5).

b. Subtract the base state, (3.8.9), (3.8.10) from these equations.

c. Omit terms that are quadratic in the perturbation quantities.

d. Eliminate ˆp and ˆu from the ˆw equation (z-momentum equation) by using

continuity (3.8.2) and x-momentum (3.8.3) equations.

The resulting two equations for the perturbation variables ˆw and

θ are

∂

∂t

(∇

ˆw) −Pr ∇

(∇

ˆw) = RaPr

θ (3.8.11)

∂

∂t

−∇

θ = ˆw (3.8.12)

Because both equations (3.8.11) and (3.8.12) are linear, we can use separation

of variables. For periodic solution in the x direction, we can assume

ˆw(x, z, t) = w



(z)e

σ t

Ikx

θ(x, z, t) = θ



(z)e

σ t

Ikx

(3.8.13)

In (3.8.13), σ is the ampliﬁcation factor; it can be shown (Kundu and Cohen,

2008, p. 475) that it is a real number for Ra > 0andI

=−1. The wave number

k is also real if the solution is periodic as x →∞. We also note that if σ = 0, the

disturbances remain neutral; if σ<0, disturbances decay in time; and if σ>0,

disturbances amplify, resulting in the formation of Benard cells, which will be

periodic in x with a wave number k. Then, w



gives the amplitude distribution

of these cells in the z direction. With the substitution of (3.8.13) into (3.8.11)

188 VISCOUS FLUID FLOWS

and (3.8.12), we obtain



−(D

−k

)



−k



=−k

(Ra)θ



(3.8.14)

D ≡

[σ − (D

−k

)]θ



= w



(3.8.15)

These equations are homogeneous ordinary differential equations, with the fol-

lowing homogeneous boundary conditions:

z = 0, 1 w



= 0

z = 0, 1 Dw



= 0

z = 0, 1 θ



= 0

(3.8.16)

The boundary condition Dw



= 0 follows directly from the incompressible con-

tinuity equation evaluated at the wall (z = 0) for a viscous ﬂuid satisfying the

no-slip boundary condition. Accordingly, at the wall u



(0, t) = 0 and there-

fore (∂u



/∂x) = 0. Hence, from continuity, (∂w



/∂z) = 0 and, consequently,



= 0 must be satisﬁed.

We now have a coupled system of two homogeneous equations, the ﬁrst fourth

order and the other second order, both with homogeneous boundary conditions.

Given Ra, Pr and the wave number k, these equations become an eigenvalue

problem for σ . The eigenfunctions w



(z) and θ



(z) give the amplitude distribution

of the perturbations.

A very useful simpliﬁcation of this problem is the search for neutral stability

when σ = 0. For this case the governing equations (3.8.14) and (3.8.15) can be

written as a coupled system of equations:

−k

)θ



= 0 (3.8.17)

−k

)



−k

(Ra)θ



= 0 (3.8.18)

Writing these equations in vector-matrix form, with I as the identity matrix,

we obtain



−k

I) I

0(D

−k



−Ra



I 0









= 0 (3.8.19)

Equation (3.8.19) with the homogeneous boundary conditions (3.8.16) comprises

a generalized eigenvalue problem where for given wave number, k, the desired

eigenvalue is the minimum Ra, and the solution vector {



} contains the

corresponding eigenfunctions.

A numerical solution for this problem can be obtained by discretizing the

difference operator D by second-order central ﬁnite differences. At the boundary

points corresponding to the solid plates placed at z = 0, 1, one-sided differences

FLOW STABILITY AND PSEUDO-SPECTRAL METHODS 189

will be used. Consequently, the following ﬁnite difference formulae are

considered:

Operator Derivative Formula Order

Forward





−3w



+4w



i+1

−w



i+2

2z

z

Backward







−4w



i−1



i−2

2z

z

Central







i+1

−2w



i−1

z

Central







i+2

−4w



i+1

+6w



−4w



i−1



i−2

z

(3.8.20)

Let us now consider the discrete form of (3.8.17), which is obtained using

(3.8.20), with the homogeneous boundary conditions, assuming that the grid

point index i = 1 corresponds to the lower wall and i = imax corresponds to

the upper wall. With h = z, these ﬁnite-difference equations are listed below:



= 0



i−1

−







i+1



= 0



imax

= 0 (3.8.21)

We also deﬁne the following parameters for later use:

≡

≡−





For (3.8.18), we obtain



= 0

−



−



= 0 (for boundary condition Dw = 0

at the lower plate)



i−2

−







i−1







−







i+1



i+2

−k

(Ra)θ



= 0



imax

−



imax−1



imax−2

= 0 (for boundary condition Dw = 0

at the upper plate)



imax

= 0 (3.8.22)

190 VISCOUS FLUID FLOWS

Similarly, we deﬁne the following parameters:

≡

≡−





≡





Considering a computational mesh of 7 grid points including the lower and

upper boundaries, we write (3.8.21) and (3.8.22) in matrix form:

⎡

⎢

⎣

10 0

01 0

100

−3

−1

0 b

−2

00 1

⎤

⎥

⎦

⎡

⎢

⎣

⎤

⎥

⎦



−Ra

⎡

⎢

⎣

⎤

⎥

⎦

⎡

⎢

⎣

⎤

⎥

⎦



(3.8.23)

FLOW STABILITY AND PSEUDO-SPECTRAL METHODS 191

which has the general form

[A − Ra ·B]









= 0





={θ



, θ



, ..., θ



}



={w



, w



, ..., w



}

(3.8.24)

It is important to note that the 1st and the 7th rows of the coefﬁcient matrices

A and B in (3.8.23) have been modiﬁed to impose the boundary conditions on



at the lower and upper plates, respectively. The boundary conditions for w



the lower plate are imposed by modifying rows 8, 9 in both coefﬁcient matrices

A and B; the boundary conditions on w



at the upper plate are imposed by

modifying rows 13 and 14 in A and B.

The generalized eigenvalue problem (3.8.24) can be very conveniently solved

by the MATLAB command eig(A, B)forA and B square matrices. For example,

the command [X ,D] = eig(A,B) returns a diagonal matrix D with the eigenvalues

in the diagonal and a matrix X with corresponding eigenvectors as columns.

Problem 3.14 Compute the neutral stability curve for Benard convection

between rigid–rigid boundaries using the formulation given above to calculate

the critical value Ra

, and the corresponding wave number. It is important to

note that a range of k values are speciﬁed, 0.5 ≤ k ≤ 10.0, and a full set of

eigenvalues are calculated for each value of k as the program is stepped up by

an amount k = 0.1. For each k value, the minimum Ra is selected, and Ra

corresponds to the minimum of these Ra values. The computation can start with

about 30–40 grid points, but as the value of Ra

is approached, the solution

requires signiﬁcantly higher mesh resolution of about 150 grid points. A closed

form solution for this problem is given by Jeffreys (1928), which reads

(π

)



1 −

(π

)



κ =

tanh



sec h



(3.8.25)

a. Plot the computed neutral stability curve.

b. Find the critical Rayleigh number.

c. Plot the corresponding eigenfunctions.

d. Graphically compare your results with the analytic solution given by

Jeffreys (3.8.25).

Next, we consider a canonical example concerning the hydrodynamic stability

of plane channel ﬂow formed by a pressure gradient between two parallel plates.

We will again consider two-dimensional, unsteady, incompressible ﬂow. The