Benzoni-Gavage S., Serre D. Multi-dimensional Hyperbolic Partial Differential Equations: First-order Systems and Applications
Подождите немного. Документ загружается.

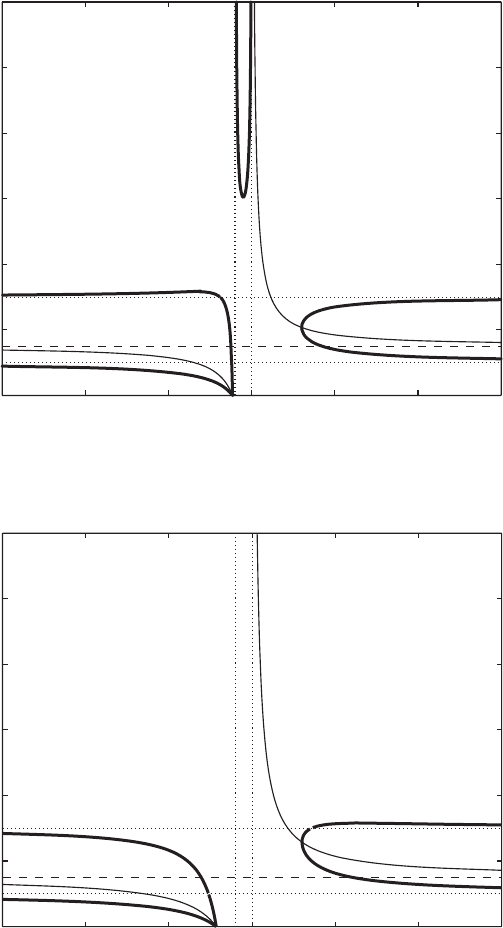
Stability conditions 435
−15 −10 −5 0 5 10 15
0
1
2
3
4
5
6
The algebraic curve p=0 and the graph of x0
Figure 15.1: The curve P (thick solid line) in an example of Case 1a (M =0.5,
r =1.15).
−15 −10 −5 0 5 10 15
0
1
2
3
4
5
6
The algebraic curve p=0 and the graph of x0
Figure 15.2: The curve P (thick solid line) in an example of Case 1b (M =0.5,
r = 4); the upper branch is out of range.
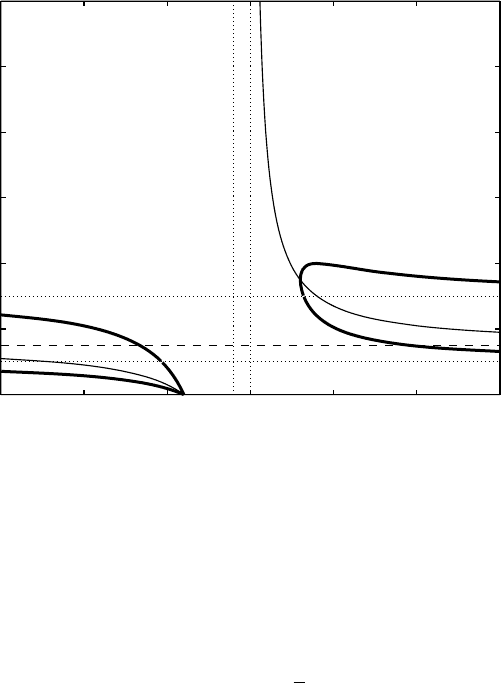
436 Shock stability in gas dynamics
−15 −10 −5 0 5 10 15
0
1
2
3
4
5
6
The algebraic curve p=0 and the graph of x0
Figure 15.3: The curve P (thick solid line) in an example of Case 2 (M =0.5,
r =2.15); the upper branch is out of range.
But x
0
(k) is now greater than both of them. Therefore, we are in the same
situation as before. The positive root of p yields a real root of f.
r
for M
2
r+1−M
2
<k<1+M,wehavea
2
(k) < 0anda
2
(k) p(x
0
(k),k) < 0.
Therefore, p(·,k) has two real roots of opposite signs and x
0
(k)isin
between. The negative one is such that
( k − (1 − M
2
))(x − x
0
) < 0 ,
and it is the contrary for the positive one. Thus, none of them yields a
root of f. The positive root goes to −sign (a
1
a
2
) ∞ =+∞ when k goes to
1+M.
r
for 1 + M<k,wehavea
2
(k) > 0anda
2
(k) p(x
0
(k),k) > 0. Therefore,
p(·,k) has either two reals roots of the same sign or two conjugated complex
roots. And p(·,k) has one real root going to −sign (a
1
a
2
) ∞ = −∞ when
k goes to 1 + M. Therefore, there exists ε>0 such that for 1 + M<
k<1+M + ε, p(·,k) has two negative real roots, and x
0
(k) is greater
than both of them. (This is also the case for large enough k due to the
parabolic branch mentioned above.) As before, none of them yields a root
of f. In general, p has conjugated complex roots on some interval [K, L]
with K ≥ 1+M + ε. But these cannot give rise to any complex zero of
f, by Rouch´e’s theorem and a connectedness argument.

Stability conditions 437
Case 1b
r
for k<M
2
r +1− M
2
, the situation is exactly as in Case 1a.
r
for M
2
r +1− M
2
<k<1+M, as in Case 1a, p(·,k) has two real
roots of opposite signs, x
0
(k) is in between, and none of them yields a root
of f. The only difference is that it is the negative root that goes to infinity
when k goes to 1 + M.
r
for 1 + M<k, as in Case 1a, p(·,k) has either two reals roots of the
same sign or two conjugated complex roots. This time p(·,k) has one real
root going to −sign (a
1
a
2
) ∞ =+∞ when k goes to 1 + M. Therefore,
there exists ε>0 such that for 1 + M<k<1+M + ε, p(·,k)hastwo
positive real roots, and x
0
(k) is less than both of them. As before, none of
them yields a root of f. For larger k, the conclusion that f keeps having
no roots follows in the same way as in Case 1a.
Case 2
r
for k<1+M , the situation is similar as in Case 1 when k<M
2
r+1−M
2
.
r
for 1 + M<k<M
2
r +1− M
2
, a
2
(k) > 0anda
2
(k) p(x
0
(k),k) < 0.
Therefore, p(·,k) has positive real roots and x
0
(k) is in between. Only the
smallest one yields a (real) root of f, because
( k − (1 − M
2
))(x − x
0
) < 0 .
The greatest one goes to −sign (a
1
a
2
) ∞ =+∞ when k goes to 1 + M.
r
for M
2
r +1− M
2
<k,asinCase1b,p(·,k) has two positive real roots,
and x
0
(k) is less than both of them, as long as k is not too large. None of
them yields a root of f. The conclusion is the same as in other cases.
15.2.2 Notable cases
The uniform stability condition (15.2.16) may equivalently be rewritten as
(Γ + 1) M
2
v
0
− v
v
< 1 .
It is obviously satisfied if v
0
<v, which characterizes expansive shocks,assoon
as Γ ≥−1. Using that M
2
= v
2
j
2
/c
2
and the jump relation (13.4.34), another
statement of the uniform stability condition is
(Γ + 1) v
p − p
0
c
2
< 1 .
Ideal gases Since for ideal gases,
Γ+1=γ =
vc
2
p
,

438 Shock stability in gas dynamics
the uniform stability condition here above is obviously always satisfied. There-
fore, we have the following.
Theorem 15.2 All Lax shocks are uniformly stable in ideal gases.
This result has been well-known since Majda’s work [125]. It was, nevertheless,
questioned, wrongly, very recently (see [42] for more details).
Weak shocks As noted by M´etivier in [133], the uniform stability condition
(15.2.16) is satisfied for shocks of small enough amplitude. As a matter of fact,
k tends to 2 and r tends to 1 when the amplitude of the shock goes to 0.
Isentropic case We claim that stability conditions for isentropic gas dynamics
are a byproduct of stability conditions for complete gas dynamics, because isen-
tropic stability conditions are merely obtained by suppressing the penultimate
row and column of ∆. This just amounts to setting Γ = 0, or equivalently
k = 2, in the complete stability conditions. Therefore, we see from (15.2.14) that
the one-dimensional condition reduces to 1 + M = 0, which is always satisfied.
Accordingly, the first inequality in the weak multidimensional stability condi-
tion (15.2.15) is trivially satisfied. And the uniform multidimensional stability
condition reduces to
M
2
( r − 1) < 1 , (15.2.24)
or equivalently
p − p
0
−vp
v
< 1 .
This condition holds true in particular for the γ-law p =cstv
−γ
with γ ≥ 1.
15.2.3 Kreiss symmetrizers
The explicit construction of Kreiss’ symmetrizers given in Chapter 14 for regular
Initial Boundary Value problems is easily generalized to the shock stability
problem.
To stay close to the notations of Chapter 12, we denote here U =(v, u,s)
the set of thermodynamic and kinematic dependent variables, and
U : R
d−1
× R
+
× R → R
d+2
× R
d+2
× R × R
d−1
(y, z, t) → ( U
−
(y, z, t),U
+
(y, z, t),∂
t
χ(y, t), ∇
y
χ(y, t))
the sought shock solution, where χ is the unknown front and U
±
=(v
±
, u
±
,s
±
)
correspond to the unknown states on either side (both defined on R
d−1
× R
+
× R
after a suitable change of variables, see Chapter 12). For X =(y,z,t,η,τ) ∈
R
d−1
× R
+
× R
d−1
× C, we denote by A
U
(X)the2(d +2)×2(d + 2) matrix
obtained, as in the abstract framework of Chapter 12, through the following
successive transformations of the Euler equations on both sides of the unknown
front:
Stability conditions 439
i) fixing of the free boundary,
ii) linearization about U,
iii) freezing of coefficients at point (y,z,t),
iv) Fourier–Laplace transform, which amounts to replacing ∂
t
by its symbol
τ and ∂
y
j
by its symbol iη
j
for j ∈{1,...,d− 1}.
There is no need to write the matrix A
U
(X) explicitly, for we know it is block-
diagonal,
A
U
(X)=
A
l
(X)
A
r
(X)
,
and we know from Section 14.4 reduced forms of the blocks A
l,r
(X). Indeed,
if we denote by U
l
= U
−
(y,z,t) the supersonic state and by U
r
= U
+
(y,z,t)
the subsonic state of the fluid with respect to the shock front, for Re τ>0the
dispersion equation
(τ − u
l
ω)
2
= c
2
l
(ω −η
2
)
has two roots of positive real parts, which we denote by ω
l
1
and ω
l
2
, while the
analogous dispersion equation for the subsonic state
(τ − u
r
ω)
2
= c
2
r
(ω −η
2
)
has one root of positive real part, which we denote by ω
r
+
, and one of negative
real part, which we denote by ω
r
−
. Denoting also ω
l,r
0
:= τ/u
l,r
,wehavethat
A
l
(X) is similar to
A
l
(X)=
ω
l
0
I
d
ω
l
1
ω
l
2
≥ 0 ,
while A
r
(X) is similar to
A
r
(X)=
−ω
r
0
I
d
a
,
where the 2 × 2blocka is either diag(−ω
r
+
, −ω
l
−
)ifω
r
+
and ω
r
−
are distinct (i.e.
if τ
2
+(c
2
r
− u
2
r
) η
2
) = 0) or a Jordan block. Therefore, we can find a Kreiss
symmetrizer of the form
R
U
(X)=
µI
d+2
R
r
(X)
,
where the block R
r
(X) is of the same form as the Kreiss symmetrizer constructed
in Section 14.4 for the standard, subsonic inflow IBVP. More precisely, R
r
(X)is
locally similar (in the same basis as A
r
(X)) to
R
r
(X)=
−I
d
r
,

440 Shock stability in gas dynamics
where r is merely diag(−1,µ)ifω
r
+
and ω
r
−
are distinct. Here above, of course,
the parameter µ has to be chosen large enough to absorb ‘bad’ terms.
This construction completes the proof of Lemma 12.1 in the case of gas
dynamics.
15.2.4 Weak stability
In the case of weak multidimensional stability (i.e. with (15.2.15)), it is still
possible to derive energy estimates, but of course with a loss of derivatives. This
question was investigated in detail by Coulombel [38, 39]. Here we just want to
address the order of vanishing of the Lopatinski˘ı determinant, which is crucially
related to those weak energy estimates.
The order of vanishing of the Lopatinski˘ı determinant is indeed tightly related
to the order of the corresponding root x of the polynomial p defined in (15.2.21).
Proposition 15.2 If z is a double root of the function f defined by (15.2.17)
and (15.2.18),withr =0and M
2
< 1, then z
2
is a double root of the polynomial
p(·,k) defined in (15.2.21).
Proof We first note that z = 0 is not possible since r = 0. A little algebra then
shows that f(z)=f
(z) = 0 implies
a
2
(k) z
2
+
a
1
(k)
2
=0,
where a
m
(k) denotes as before the coefficient of order m of p(·,k). Hence z
2
can only be a double root of the second-order polynomial p(·,k). Beyond this
elementary proof, a cleverer one makes use of the fact that p is a resultant.
We recall indeed that p is the resultant with respect to the y variable of the
polynomials F and G defined in (15.2.22) and (15.2.23). A basic property of
resultants says there exist polynomials R(x, y)andQ(x, y) (in fact, Q(x)since
F is of degree 1 in y) such that
p(x)=F (x, y) R(x, y)+G(x, y) Q(x) .
In particular, this implies the identity
p(z
2
)=f(z) R( z
2
,zg(z)).
Differentiating once, we obtain that
2 zp
(z
2
)=f
(z) R( z
2
,zg(z))
if f(z) = 0, and thus p
(z
2
)=0iff
(z) is also zero (recall that z = 0 whenever
f(z)=0).
PART V
APPENDIX
This page intentionally left blank
A
BASIC CALCULUS RESULTS
The celebrated Gronwall Lemma is used repeatedly in this book. We state our
most useful versions of it for convenience.
Lemma A.1 (Basic Gronwall Lemma) If u and f are smooth functions of
t ∈ [0,T] such that
u(t) ≤ C
0
+ C
1
t
0
( u(τ)+f(τ ))dτ ∀t ∈ [0,T] ,
with C
0
∈ R and C
1
> 0 then
u(t) ≤ e
C
1
t
C
0
+ C
1
t
0
f(τ)dτ
∀t ∈ [0,T] .
Proof The only trick in the proof is to show the final estimate for the right-
hand side
v(t):=C
0
+ C
1
t
0
( u(τ)+f(τ ))dτ
of the original one. Since
v
(t)=C
1
( u(t)+f(t))≤ C
1
( v(t)+f(t))
we easily get the inequality
e
− C
1
t
v(t) ≤ v(0) + C
1
t
0
e
− C
1
τ
f(τ)dτ,
of which the claimed estimate is only a rougher version.
A slightly more elaborate version that we often use is the following.
Lemma A.2 (Gronwall Lemma) If u and f are smooth functions of t ∈ [0,T]
such that
u(t) ≤ C
0
e
γt
+ C
1
t
0
e
γ (t−τ )
( u(τ)+f(τ ))dτ ∀t ∈ [0,T]
with C
0
∈ R and C
1
> 0 then
u(t) ≤ C
0
e
(C
1
+γ) t
+ C
1
t
0
e
(C
1
+γ)(t−τ)
f(τ)dτ ∀t ∈ [0,T] .
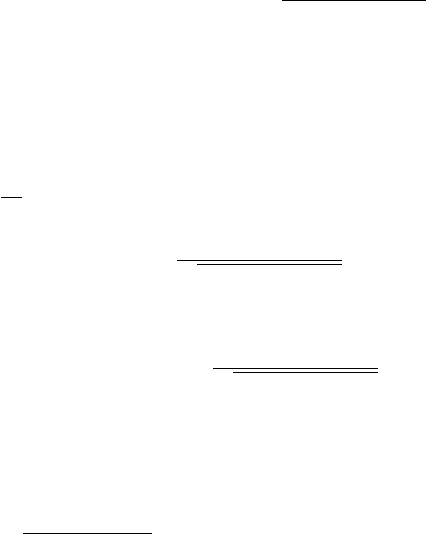
444 Basic calculus results
Lemma A.3 (‘Multidimensional’ Gronwall Lemma) Assume L⊂R
d+1
is a
lens foliated by hypersurfaces H
θ
and denote
L
θ
=
ε∈[0,θ]
H
ε
⊂L
for θ ∈ [0, 1].Ifu is a smooth function in the neighbourhood of L such that
H
θ
|u|≤C
H
0
|u| +
L
θ
|u|
∀θ ∈ [0, 1]
then there exists C
depending only on C and L such that
H
1
|u|≤C
H
0
|u|.
Proof The proof relies on the same trick as before but requires a little multi-
dimensional calculus. Introducing parametric equations x = X(y, θ), t = T (y,θ)
(y ∈ Ω ⊂ R
d
)forH
θ
we have
H
θ
|u| =
Ω
|u(X(y, θ),T(y,θ))|
|d
y
X|
2
+ |d
y
T |
2
dy,
L
θ
u =
θ
0
Ω
|u(X(y, ε),T(y, ε))||J(y, ε)|dy dε, J =
d
y
X∂
θ
X
d
y
T∂
θ
T
.
Hence
d
dθ
L
θ
|u| =
Ω
|u(X(y, θ),T(y,ε))||J(y, θ)|dy
≤ max
¯
Ω×[0,1]
|J|
|d
y
X|
2
+ |d
y
T |
2
H
θ
|u|.
Then we easily get the wanted estimate with
C
=max
¯
Ω×[0,1]
exp
C
|J|
|d
y
X|
2
+ |d
y
T |
2
.
Lemma A.4 (Discrete Gronwall Lemma) If a is a non-negative continuous
function of s ∈ [0,t] and b is a non-decreasing function of s ∈ [0,t] such that
a(s + ε) − a(s)
ε
≤ C ( ε + b(s)+a(s + ε))
for all (ε, s) with 0 <ε≤ ε
0
∈ (0,t), s ∈ [0,t− ε], then
a(t) ≤ e
Ct
( a(0) + b(t)).
