Benzoni-Gavage S., Serre D. Multi-dimensional Hyperbolic Partial Differential Equations: First-order Systems and Applications
Подождите немного. Документ загружается.

13
THE EULER EQUATIONS FOR REAL FLUIDS
The mathematical theory of gas dynamics is often ‘limited’ to polytropic ideal
gases (see, for instance, [50,55,117], etc). Here, we are interested in more general
compressible fluids, which can be gases (e.g. non-polytropic ideal gases) but also
liquids or even liquid–vapour mixtures (e.g. van der Waals fluids). We call them
real because of their possible complex thermodynamical behaviour. (This was
initially motivated by the PhD thesis of Jaouen [90].) Still, we are aware that they
are not that real, as long as dissipation due to viscosity and/or heat conduction is
neglected: except for the discussion on the admissibility of shock waves (in Section
13.4), our subsequent analysis does not take into account dissipation phenomena,
to stay within the theory of hyperbolic PDEs. Our aim is to investigate, for
inviscid and non-heat-conducting fluids, the Initial Boundary Value Problem and
the stability of shock waves, by means of the methods described in the previous
parts of the book.
The present chapter is devoted to generalities on the thermodynamics and
the equations of motion for real compressible fluids (in the zero viscosity/heat
conduction limit), and to basic results regarding smooth solutions and (planar)
shock waves. Some material is most classical and some is inspired from an
important but not so well-known paper by Menikoff and Plohr [130]. Boundary
conditions and stability of shocks will be addressed in separate chapters (Chapter
14 and Chapter 15, respectively).
13.1 Thermodynamics
We consider a fluid whose specific internal energy e is everywhere uniquely (and
smoothly) determined by its specific volume v and its specific entropy s.This
amounts to assuming the fluid is endowed with what we call (after Menikoff and
Plohr [130]) a complete equation of state e = e(v, s).
The fundamental thermodynamics relation is
de = −p dv + T ds, (13.1.1)
where p is the pressure and T the temperature. To avoid confusion when per-
forming changes of thermodynamic variables we adopt a physicists’ convention:
throughout the chapter, we shall specify after a vertical bar the variable main-
tained constant in partial derivatives with respect to thermodynamic variables.

386 The Euler equations for real fluids
Using this convention, we may rewrite (13.1.1) as
p = −
∂e
∂v
s
,T=
∂e
∂s
v
. (13.1.2)
We shall use four thermodynamic non-dimensional quantities.
r
The first one is the adiabatic exponent, defined by
γ := −
v
p
∂p
∂v
s
. (13.1.3)
We have adopted here the same convention as in [130]. Except in the case
of polytropic gases, this coefficient γ differs from the widely used ratio of
heat capacities.
r
Another important one is called the Gr¨uneisen coefficient, defined by
Γ:=−
v
T
∂T
∂v
s
. (13.1.4)
r
By (13.1.2), γ and Γ are related to the Hessian of e through the equalities
γ
p
v
=
∂
2
e
∂v
2
, Γ
T
v
= −
∂
2
e
∂s∂v
. (13.1.5)
The last relevant quantity regarding D
2
e is
δ :=
pv
T
2
∂T
∂s
v
=
pv
T
2
∂
2
e
∂s
2
. (13.1.6)
It is related to the heat capacity at constant volume
c
v
:=
T
∂
2
e
∂s
2
v
=
∂e
∂T
v
(13.1.7)
through the simple formula
c
v
δ =
pv
T
. (13.1.8)
r
Finally, a ‘higher-order’ coefficient will be of interest. Following [130], we
denote
G := −
1
2
v
∂
3
e
∂v
3
s
∂
2
e
∂v
2
s
. (13.1.9)
Standard thermodynamics requires that γ be positive and e be a convex
function of (v, s), which amounts to asking γδ −Γ
2
≥ 0. The positivity of γ

Thermodynamics 387
means that p is increasing with the density ρ := 1/v, thus allowing the definition
of sound speed c by
c :=
∂p
∂ρ
s
=
5
γ
p
ρ
. (13.1.10)
Using c and ρ, we may rewrite G as
G =
1
c
∂(ρc)
∂ρ
s
. (13.1.11)
We shall see that the sign of G plays a crucial role in both the non-linearity of
the acoustic fields and in the admissibility of shock waves.
The following definition refers to independent works of Bethe [16] and Weyl
[218] in the 1940s (also see [69]).
Definition 13.1 We call a Bethe–Weyl fluid any fluid endowed with a complete
equation of state, with e bounded by below, such that the pressure and temperature
defined in (13.1.2) are positive, and the associated coefficients γ, Γ, δ and G
(defined in (13.1.3), (13.1.4), (13.1.6) and (13.1.9), respectively) satisfy
γ>0 ,γδ≥ Γ
2
, Γ > 0 , G > 0 (13.1.12)
and
lim
ρ→ρ
max
p(ρ, s)=∞. (13.1.13)
As mentioned above, the first two requirements in (13.1.12) come from standard
thermodynamics. The condition Γ > 0 is not imposed by thermodynamics, but
it often holds true (even though there are simple counterexamples, like water
near 0
◦
C, as pointed out by Bethe). It ensures in particular that the isentropes
do not cross each other in the (v,p)-plane. And the condition G > 0 means that
these isentropes are strictly convex. If this is not the case, the fluid may exhibit
weird features, as was pointed out by Thompson and Lambrakis [209] (we warn
the reader that G is denoted Γ in that paper). Note that when Γ > 0, i.e. when
p is increasing with entropy at constant volume, the fact that δ is positive is
equivalent to
∂T
∂p
v
> 0 . (13.1.14)
This condition is at least consistent with everyday experience (with air, water,
etc.).

388 The Euler equations for real fluids
Refined conditions were later introduced by Smith [197], in connection with
the resolution of the Riemann problem
1
. We retain here the weakest of Smith’
conditions.
Definition 13.2 We call a Smith fluid a Bethe–Weyl fluid satisfying the addi-
tional condition
Γ < 2 γ. (13.1.15)
Example
Ideal gas The ideal gas law is known to be
pv = RT , (13.1.16)
where R is a constant. (If v stands for the molar volume instead of the specific
volume, R is universal and equals approximately 8.3144 J · K
−1
· mol
−1
.) We
readily see that (13.1.14) is satisfied for v>0. Then it is easy to check that
(13.1.16) is compatible with the fundamental relation (13.1.1), or equivalently
(13.1.2), provided that
e = ε
v
−R
exp(s)
,
where ε is any (smooth) function that is bounded by below on (0, +∞). With a
complete equation of state of this form, an easy calculation shows that
γ =Γ+1 and δ =Γ.
Therefore, the first three inequalities in (13.1.12) are altogether equivalent to
γ>1. Note that in view of (13.1.8) we have
Γ=δ =
R
c
v
.
Thus (13.1.15) is trivially satisfied. Regarding G, there is no simple expression
for general functions ε. The next example concerns power functions ε, for which
quite a nice expression of G is available.
Polytropic gas Polytropic gases are merely ideal gases for which c
v
is constant
and ε is the power function
ε(u)=u
1/c
v
.
In this case, Γ, γ and δ are all constant and we have
e = c
v
T and p =(γ − 1) ρe.
The latter equality is the most famous example of an incomplete equation of state,
giving p in terms of ρ and e. Incomplete equations of state, or simply pressure
1
The Riemann problem for a one-dimensional hyperbolic system of conservation laws is a special
Cauchy problem, in which the initial data are step functions. Its resolution is crucial both for
theoretical and numerical purposes.

Thermodynamics 389
laws, are sufficient for the closure of the Euler equations (which by definition
encode the conservation of mass, momentum and total energy, see Section 13.2
below). The present pressure law, widely used in the mathematical theory of
gas dynamics, is often termed the γ-law for an obvious reason. Note that it is
only for polytropic gases that our γ coincides with the ratio of heat capacities
(see [130], p. 79b for further discussion on this topic). In addition, we find that
for polytropic gases
G =
γ +1
2
,
which is obviously positive: isentropes are indeed convex for polytropic gases. As
to the asymptotic condition (13.1.13), it holds true with ρ
max
=+∞, thanks to
the positivity of R/c
v
.
Van der Waals fluid The van der Waals law is a modification of (13.1.16) that
takes into account the finite size of molecules by imposing a positive minimum
value – the so-called covolume b>0 – for the specific (or the molar) volume,
and also some intermolecular forces through an additional term depending on a
parameter a ≥ 0. (See, for instance, [168] for more details.) The van der Waals
law reads
p =
RT
v − b
−
a
v
2
, (13.1.17)
which obviously satisfies (13.1.14) for v>b. Furthermore, (13.1.17) is compatible
with (13.1.1) and (13.1.7) with
e =((v − b)
−R
exp(s))
1/c
v
−
a
v
,
provided that c
v
is constant. Even though the constancy of the heat capacity c
v
is
notoriously false (see [168], p. 263) near critical temperature (below which liquid
and vapour phases can coexist, and whose theoretical value is T
c
=8a/(27bR),
c
v
may reasonably be considered as constant far away from the critical point.
In this case, we easily see that (13.1.13) holds true with ρ
max
=1/b,andan
equivalent way of writing e is,
e = c
v
T −
a
v
.
Some algebra then shows that
Γ=
R
c
v
v
v − b
,δ=Γ−
a/v
e + a/v
,
γ =(
R
c
v
+1)
v
v − b
+
(
R
c
v
+1)
v
v − b
− 2
a/v
2
p
390 The Euler equations for real fluids
and
G =
1
2γ
(
R
c
v
+1)(
R
c
v
+2)
v
2
(v − b)
2
+
(
R
c
v
+1)(
R
c
v
+2)
v
2
(v − b)
2
− 6
a/v
2
p
.
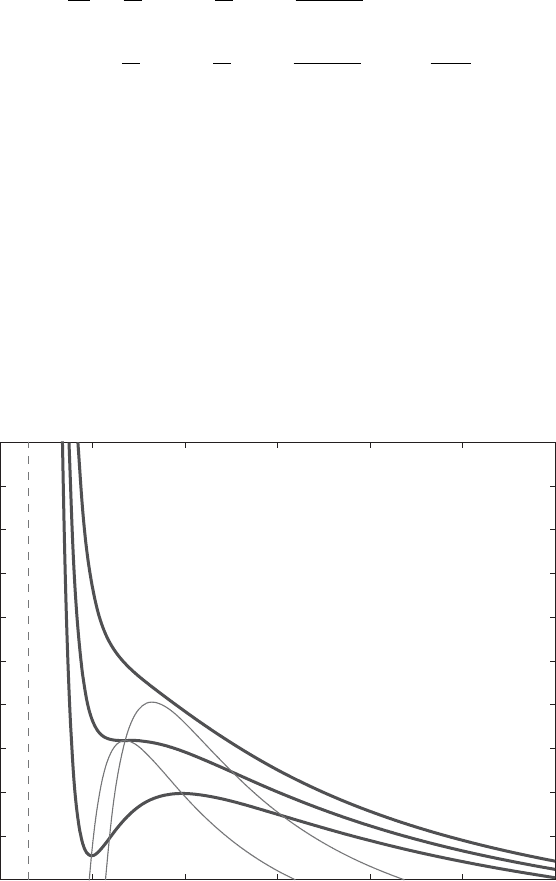
The sets {γ =0} (critical points of the isentropes) and {G =0} (inflexion points
of the isentropes) in the (v, p)-plane are depicted in Fig. 13.1, together with
three kinds of isentropes (a convex one, a non-convex monotone one and a non-
monotone one), for parameters a, b and c
v
corresponding (roughly) to water (for
which the van der Waals law is widely used, in particular in nuclear engineering,
even though it is known to be a poor approximation of reality: the adequation
coefficient, defined as the ratio of the theoretical compression factor p
c
v
c
/(RT
c
)=
3/8 and the real one, is only about 60%!).
Note The van der Waals law (13.1.17) in the special case a = 0 does not
support phase boundaries. For this reason, fluids endowed with such a law are
usually referred to as van der Waals gases. We point out that dusty gases (as
0 100 200 300 400 500 600
2
3
4
5
6
7
8
9
10
11
12
Water isentropes
Volume (cm
3
/mol)
Pressure (decabars)
Figure 13.1: Water isentropes (thick solid lines) with the van der Waals law (a,
b taken from [216], and c
v
/R =3.1).

The Euler equations 391
in [91], for instance) follow a similar law: the Mie–Gr¨uneisen-type pressure law
used in [91] is indeed of the form (13.1.17) with a =0.
13.2 The Euler equations
13.2.1 Derivation and comments
The motion of a compressible, inviscid and non-heat-conducting, fluid is gov-
erned by the Euler equations, consisting of the mass, momentum and energy
conservation laws (see, for instance, [47]),
∂
t
ρ + ∇·(ρ u)=0,
∂
t
(ρu)+∇·(ρ u ⊗ u)+∇p =0,
∂
t
ρ
1
2
u
2
+ e
+ ∇·
ρ
1
2
u
2
+ e
+ p
u
=0.
(13.2.18)
This system of (d + 2) equations contains (d + 3) unknowns, the density ρ ∈ R
+
,
the velocity u ∈ R
d
, the internal energy e ∈ R and the pressure p ∈ R.This
obviously makes too few equations for too many unknowns. The system (13.2.18)
has to be closed by adding a suitable equation of state, for example an incomplete
equation of state, or pressure law, (ρ, e) → p(ρ, e).
Simplified models are obtained by retaining only the mass and momentum
conservation laws, assuming that the motion is either isentropic or isothermal.
In this case, the pressure law reduces to ρ → p(ρ) . If a complete equation of
state is available, the isentropic pressure law is given by
p = −
∂e
∂v
s
,
and the isothermal pressure law is given by
p = −
∂f
∂v
T
,
where f := = e − Ts is the specific free energy.
We observe that an incomplete equation of state is sufficient to give sense to
the quantities γ,ΓandG originally defined in (13.1.3), (13.1.4) and (13.1.9). As
a matter of fact, if (13.1.1) holds then (v, s) → (v, e) is a local diffeomorphism
provided that T>0, and the partial derivatives in the old variables are given in
terms of the new variables by
∂
∂v
s
=
∂
∂v
e
− p
∂
∂e
v
,
∂
∂s
v
= T
∂
∂e
v
. (13.2.19)

392 The Euler equations for real fluids
Therefore, alternative formulae are
γ = −
v
p
∂p
∂v
e
− p
∂p
∂e
v
, Γ=v
∂p
∂e
v
, (13.2.20)
G =
1
2
γ +1 −
v
γ
∂γ
∂v
e
− p
∂γ
∂e
v
, (13.2.21)
which also make sense if it is just an incomplete equation of state that is given.
Equation (13.2.21) may seem less obvious to the reader than (13.2.20). It is
merely obtained by rewriting
G = −
v
2
2 γp
∂
∂v
γp
v
s
.
13.2.2 Hyperbolicity
A classical and elementary manipulation shows that, for smooth solutions,
(13.2.18) is equivalent to
∂
t
ρ + u ·∇ρ + ρ ∇·u =0,
∂
t
u +(u ·∇) u + ρ
−1
∇p =0,
∂
t
e + u ·∇e + ρ
−1
p ∇·u =0.
(13.2.22)
Therefore, the hyperbolicity of (13.2.18) is equivalent to the uniform real diago-
nalizability of the matrix
A(U; n):=
u · n ρ n
T
0
ρ
−1
p
ρ
n (u · n) I
d
ρ
−1
p
e
n
0 ρ
−1
p n
T
u · n
for all U =(ρ, u,e)andn ∈ R
d
\{0}. We have denoted for simplicity
p
ρ
=
∂p
∂ρ
e
,p
e
=
∂p
∂e
ρ
.
If ( ˙ρ,
˙
u, ˙e)
T
is an eigenvector of A(U; n) associated with an eigenvalue
λ(U; n), then
(u · n − λ(U; n)) ˙ρ + ρ n ·
˙
u =0,
ρ
−1
p
ρ
˙ρ n +(u · n − λ(U; n))
˙
u + ρ
−1
p
e
˙e n =0,
ρ
−1
p n ·
˙
u +(u · n − λ(U; n)) ˙e =0.

The Euler equations 393
We thus see that λ(U; n)=u · n is an eigenvalue of A(U; n), with a d-
dimensional eigenspace given by
{(˙ρ,
˙
u, ˙e)
T
; n ·
˙
u =0,p
ρ
˙ρ + p
e
˙e =0}.
For eigenvectors associated with other eigenvalues, we must have
p ˙ρ = ρ
2
˙e,
as we see from the first and last equations above. Taking the inner product by n
of the intermediate equation, and eliminating n ·
˙
u by means of the first equation,
we get
( p
ρ
|n|
2
− (u · n − λ)
2
)˙ρ + p
e
|n|
2
˙e =0.
This yields the dispersion relation
(u · n − λ(U; n))
2
= |n|
2
( p
ρ
+ pp
e
/ρ
2
) , (13.2.23)
of which the solutions λ(U; n) are real if and only if
p
ρ
+ pp
e
/ρ
2
≥ 0.
Recalling the definition of γ in (13.2.20), this amounts to requiring γ ≥ 0. If
γ>0 then the solutions of (13.2.23) are distinct,
λ(U; n)=u · n ± c |n|,
where c is the sound speed defined as in (13.1.10) by
c =
p
ρ
+ pp
e
/ρ
2
=
5
γ
p
ρ
.
Each of the eigenvalues u · n ± c |n|of A(U, n) has a one-dimensional eigenspace,
which is spanned by
( ρ, ±c n/|n|,p/ρ)
T
.
These very standard results are stated for later use in the following.
Proposition 13.1 The system (13.2.18), endowed with a positive pressure law
such that
γ :=
ρ
p
p
ρ
+ pp
e
/ρ
2
> 0,
is constantly hyperbolic, and strictly hyperbolic in dimension d =1. Its eigenval-
ues in the direction n are
λ
1
(U; n):=u · n − c |n|,λ
2
(U; n):=u · n ,λ
3
(U; n):=u · n + c |n|,
(13.2.24)

394 The Euler equations for real fluids
where c =
γp/ρ, with associated eigenvectors
r
1
(U; n):=
ρ
−c
n
|n|
p/ρ
,r
2
(U; n):=
− ˙αp
e
˙
u
˙αp
ρ
with
˙
u · n =0,
(13.2.25)
r
3
(U; n):=
ρ
c
n
|n|
p/ρ
.
In addition, the characteristic field (λ
2
,r
2
) is linearly degenerate, that is, dλ
2
·
r
2
≡ 0 (where d stands for differentiation with respect to U), and the fields
(λ
1
,r
1
) and (λ
3
,r
3
) (also called acoustic fields) are genuinely non-linear, that is,
dλ
1,3
· r
1,3
=0,ifandonlyif
G :=
1
c
∂
∂ρ
+
p
ρ
2
∂
∂e
(ρc) =0.
Proof It just remains to check the nature of characteristic fields. On the one
hand, it is clear that dλ
2
· r
2
≡ 0. On the other hand, we easily compute that
dλ
1,3
· r
1,3
= ρc
ρ
+ c +
p
ρ
c
e
= c G.
(Wehavesethere|n| = 1 to simplify the writing.) Of course the present
definition of G is consistent with (13.1.11) and (13.2.19).
13.2.3 Symmetrizability
There are several ways to symmetrize the Euler equations (13.2.18).
Handmade symmetrization in non-conservative variables The most
elementary way is the following, which makes sense if a complete equation of
state is given that satisfies (13.1.1), and if
∂p
∂ρ
s
> 0.
