Benzoni-Gavage S., Serre D. Multi-dimensional Hyperbolic Partial Differential Equations: First-order Systems and Applications

Подождите немного. Документ загружается.

Local uniqueness and ﬁnite-speed propagation 75

in ∂L. Hence we have



u

≤ C





u



u



where C =max

(S

 +



S

, R). By the multidimensional Gronwall’s

Lemma (see Lemma A.3 in Appendix A) we conclude that there exists C



(independent of u)sothat



u

≤ C





u

If u|

≡ 0 then clearly u|

≡ 0. 

Proof of i) The proof relies on a change of variables, transforming H into the

hyperplane {t =0} and preserving constant hyperbolicity, and on the Holmgrem

principle applied to the new (Cauchy) problem. We consider a local diﬀeomor-

phism χ such that χ(x

)=(0, 0) and



H := χ(H)={(x,



t);



t =0}.

In particular, ∇

(x,t)



t is parallel to n. We can even choose χ so that

∂



t = n

,∂



t = n

The transformed operator



L under χ is deﬁned by

(



Lv)(x,



t)=L(v ◦ χ)(x, t).

More speciﬁcally, it reads



L =



∂







∂



−



where



(x,



t)=n



(x, t) ,



(x,



t)=∂

x



(∂

x

(x, t)

and



B(x,



t)=B(x, t). Note that



(0, 0) is an invertible matrix since n(x

) ∈

char(x

). Furthermore, we have

τ



(x,



t)+



A(x,



ξ)=(τn

+ λ ) I

+ A(x, t, ξ + τν), (2.2.20)

where ν =(n

, ···,n

)and

λ =



ξ · ∂

x, ξ =





∇

x

Observing that

(ξ,λ)=(



ξ,0) dχ(x, t)andn =(ν, n

)=(0, 1) dχ(x, t),

76 Linear Cauchy problem with variable coeﬃcients

we see that (ξ,λ)and(ν, n

) are not parallel, unless



ξ = 0. By assumption, either

n(x

)or−n(x

) belongs to Γ(x

). Then we know from Theorem 1.5 of

Chapter 1 that the operator is constantly hyperbolic in the direction n,which

means that for all (ξ, λ) not parallel to n =(ν, n

), the roots σ of the polynomial

det(A(x

,ξ+ σν)+(λ + σn

)

are real with constant multiplicities. Because of (2.2.20) this shows that the roots

τ of

det( τ



(0, 0) +



A(0, 0,



ξ, τ ))

are real with constant multiplicities for



ξ = 0. This means that the transformed

operator



L is constantly hyperbolic at point (0, 0), and thus also in the neigh-

bourhood of (0, 0). Up to replacing



(x, t)by



( θ((x, t))(x, t) ) for all

α ∈{0, ···,d},whereθ is a smooth cut-oﬀ function, we can assume that



is globally deﬁned, constantly hyperbolic, and has constant coeﬃcients outside

some bounded ball. So we are led to show the result for



L instead of L,and



H := {(x,



t);



t =0} instead of H.

From now on we drop the tildas. The (hyperbolic system associated with)

operator L

∗

meets the assumptions of Theorem 2.3. Thus Theorem 2.6 applies

to L

∗

. This will enable us to apply the Holmgren principle to L.

We must show the existence of a neighbourhood N of (0, 0) such that

if u is a C

solution of Lu =0 in N and u(x, 0) = 0 for (x, 0) ∈ N then

u(x, t) = 0 for all (x, t) ∈ N . Without loss of generality, we can consider a conical

neighbourhood N , foliated by the hypersurfaces with boundary

:= {(x, t); θ

x

− V

( t − θT )

+ θ

(1 − θ)=0,

0 ≤ t ≤ θT, x≤VT},θ∈ [0, 1) .

(The reader may refer to Fig. 2.3.) Choosing

V =max{|λ

(x, t, ξ)|; ξ =1},

where λ

(x, t, ξ) denote, as usual, the eigenvalues of A(x, t, ξ) (recall that

A(x, t, ξ) has been modiﬁed to be independent of (x, t) outside a bounded ball), it

is not diﬃcult to show that all the hypersurfaces H

are space-like, as H

⊂H.

To be precise, one can compute that a unit normal vector to H

at point

(x, t)readsn =(ν, n



N/



N where



N := ( θ

x, V

(θT − t) ). And thus the

matrix (A(x, t, ν)+n

) has eigenvalues





N



(θT − t)+λ

(x, t, θ



By deﬁnition of V ,wehave

|λ

(x, t, θ

x)|≤Vθ

x,

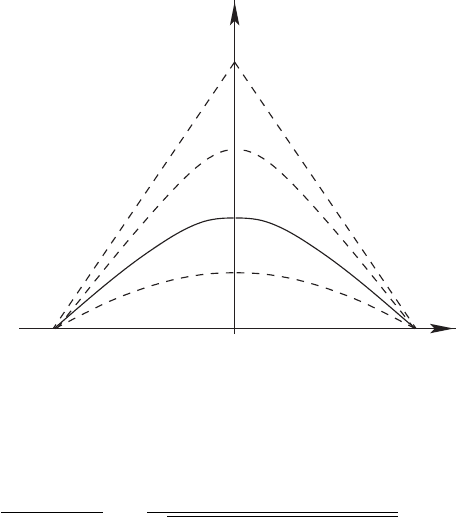
Local uniqueness and ﬁnite-speed propagation 77

V T

Figure 2.3: Foliation of a conical neighbourhood N of (0, 0)

and thus



(x, t, θ

(θT − t)



≤

x



x

+ θ

(1 − θ)

< 1onH

This proves that µ

> 0 and thus n belongs to −Γ. Therefore, H

is space-like.

Now, similarly as in the ﬁrst part of the proof, we can transform by change

of variable the problem



∗

ϕ =0,

ϕ|

= g

(2.2.21)

for g ∈ D (H

) into a standard Cauchy problem



∗

ϕ =0,

ϕ|



t=0

= g,

with

∗

being constantly hyperbolic and having constant coeﬃcients outside a

bounded ball. So by Theorems 2.3 and 2.6 the problem (2.2.21) admits a unique

smooth solution ϕ. Now, denoting by L

the lens lying in between H

and H

we have for all C

solution u of Lu =0inN



(ϕ, Lu) −



∗

ϕ, u)=



(g, (n



) u) −



(ϕ, u),

78 Linear Cauchy problem with variable coeﬃcients

where n =(n

, ···,n

) denotes the normal vector to H

.Thusifu(x, 0) = 0

for all (x, 0) ∈ N we see that



( g, (n



) u )=0.

Since this holds for any g this implies that



) u ≡ 0

on H

. But the matrix (n



) is known to be invertible since n does

not belong to the characteristic cone. Finally, this shows that u ≡ 0onH

for

all θ. 

Theorem 2.10 has a counterpart/consequence in terms of ﬁnite-speed propa-

gation, which is as follows.

Theorem 2.11

i) We assume that the system (2.0.1) is constantly hyperbolic and has

constant coeﬃcients outside a compact set. We also take f ≡ 0,andset

V =max{|λ

(x, t, ξ)|; ξ =1},

with λ

(x, t, ξ) the eigenvalues of A(x, t, ξ). To any point (X, T) ∈ R

(0, +∞) we associate the conical set

C :=



0<t<T

Ω(t) ×{t} with Ω(t):={x ; x − X <V(T − t) },

0 ≤ t<T.

If u ∈ C

([0,T]; H

) is a (weak) solution of (2.0.1) (with s ∈ R) such that

Ω(0)

=0, then u|

=0.

ii) Assuming that the system (2.0.1) is Friedrichs symmetrizable (and still

f ≡ 0), the same result holds on changing the balls Ω(t) to the convex sets

Ω(t):=

ξ=1

{x ; v(ξ)(t − T )+ξ · (x − X) ≤ 0 },

where

v(ξ):=max

(x,t)

max {v ∈ R ;(ξ,v) ∈ char(x, t) }.

Proof i) We ﬁrst show the result for u ∈ C

× [0,T]) a smooth solution.

The proof is based on a connectedness argument using Theorem 2.10 i).Wetake

ε ∈ (0,T) and deﬁne T

= T −ε,

:= {x ;0<t<T

, x − X <V(T

− t) }.

Local uniqueness and ﬁnite-speed propagation 79

Similarly as in the proof of Theorem 2.10 i), we can construct space-like surfaces

, depending smoothly on θ, such that



θ∈(0,1)

and H

⊂ Ω(0).

Then, if u ∈ C

× [0,T]) is the solution of (2.0.1) and u|

Ω(0)

=0,theset

Θ:={θ ∈ [0, 1) ; u|

≡ 0 }

of course contains 0, and is a closed subset of [0, 1) by a continuity argument.

But, covering the compact sets H

by a ﬁnite number of neighbourhoods N ,

Theorem 2.10 i) also shows that Θ is open. Therefore, we have Θ = [0, 1), which

means that u ≡ 0onC

(

0<t<T

Ω(t) ×{t}.

In general, we can proceed by regularization. Setting f := Lu and g := u|

t=0

we have by assumption that f =0in

(

0<t<T

Ω(t)andg = 0 in Ω(0). Introducing

a molliﬁer ρ

in R

, the Cauchy problem

Lv = f ∗ ρ

,v|

t=0

= g ∗ ρ

has a unique solution v = u

, which is in C

× [0,T]) by Theorem 2.6. For

k large enough, we have f ∗ρ

=0inC

and g ∗ ρ

=0inH

(with the same

notations as before). We thus infer that, for k large enough, u

=0inC

by the

ﬁrst part of the proof. But the energy estimate in (2.1.14) shows that

C ([0,T ];H

)

−−−−−−−−→

n→∞

since

= f ∗ρ

C ([0,T ];H

)

−−−−−−−−→

k→∞

f = Lu and u

t=0

= g ∗ ρ

−−−−→

n→∞

g = u|

t=0

Passing to the limit, we conclude that u =0inC

ii) The proof is a natural generalization of Section 1.3.1. It is roughly the

same as in Theorem 2.10 ii), except that we are going to consider lenses L that

are only weakly space-like. Let us consider



0≤s≤T −ε

Ω(s) ×{s}.

The boundary of L

is made of three parts, the bottom T =Ω(0)×{0}, the top

=Ω(T −ε) ×{T − ε}, and the side S. The top and bottom are obviously

space-like. As regards the side, for all (y, s) ∈S, there exists ξ

such that

{(x, t);v(ξ

)(t − T )+ξ

· (x − X)=0}

is a hyperplane of support for L

at point (y, s). A normal vector to L

at point

(y, s) is necessarily of the form n =(ξ

;=v(ξ

)). By deﬁnition of v(ξ), we

know that v

is not smaller than any v such that the matrix vI

+ A(y, s,ξ

)

is singular. Therefore, all the eigenvalues of v

+ A(y, s,ξ

) are non-negative.

80 Linear Cauchy problem with variable coeﬃcients

This implies in particular that the symmetric matrix S

(y, s)(v

+ A(y, s,ξ

))

is non-negative. Therefore, integrating by parts the identity



∂

u, u)+





∂

u, u)=



(Ru, u),

(with the same notations as in the proof of Theorem 2.10ii)), we get

0 ≥



u, u)+



(Ru, u),

if u vanishes on the bottom. Then by the Cauchy–Schwarz inequality and the

deﬁniteness of S

, there exists α>0 such that



u

≤ α



u

Since this holds for all ε ∈ (0,T], we can conclude by the Gronwall Lemma. 

2.3 Non-decaying inﬁnitely smooth data

As a consequence of Theorem 2.11, we have that, under either one of the

assumptions, the Cauchy problem can be uniquely solved for any smooth data,

without any assumption on their far-ﬁeld behaviour.

Theorem 2.12 We assume that the system (2.0.1) is either constantly hyper-

bolic with constant coeﬃcients outside a compact set, or Friedrichs symmetriz-

able. Then, for f ∈ C

∞

× [0,T]) and g ∈ C

∞

), there exists a unique

u ∈ C

∞

× [0,T]) such that

Lu = f and u|

t=0

= g.

Proof Uniqueness directly follows from Theorem 2.11. Existence is based on

truncation of f and g. We take a smooth cut-oﬀ function θ and deﬁne

(x, t)=θ



x



f(x, t) ,g

(x, t)=θ



x



g(x, t)

for all positive integers k. To ﬁx the ideas, we assume that θ ≡ 1 on the unit

ball. By Theorem 2.6, there exists a unique solution u

∈ C

∞

([0,T]; H

+∞

)of

the Cauchy problem

= f

t=0

= g

Furthermore, Theorem 2.11 shows that u

is compactly supported, and that u

coincides with u

for all m ≥ k>VT on the cylinder {x≤k − VT}×[0,T].

Therefore, the sequence (u

) is convergent in C

∞

× [0,T]) and the limit solves

the Cauchy problem

Lu = f, u|

t=0

= g.



Weighted in time estimates 81

2.4 Weighted in time estimates

We conclude this chapter by an estimate that will be useful in Chapter 9. It does

not actually deal with the Cauchy problem. It gives global in time exponentially

weighted estimates. The important feature of these estimates is that the weight

depends on a parameter, denoted by γ, which has to be chosen large enough for

the estimate to hold. This gives the ﬂavour of the machinery that will be used

in Chapter 9 for the resolution of Initial Boundary Value Problems.

Theorem 2.13 We assume that the system (2.0.1) is symmetrizable with

uniform bounds on Σ(t) (including the lower bound α>0 in (2.1.6))andon

dΣ/dt for t ∈ R. We also assume that the matrix B is uniformly bounded on

d+1

. Then there exist C>0 and γ

> 0 so that for u ∈ D (R

d+1

) and γ ≥ γ

we have





−2γt

u(t)

)



1/2

≤ C





−2γt

Lu(t)

)



1/2

(2.4.22)

Remark 2.11 According to Theorem 2.2, this result applies in particular to

systems admitting a symbolic symmetrizer (see Deﬁnition 2.3) with bounds valid

for all t ∈ R.

Proof Elementary calculus yields

)

−2γt

Σ u, u

−2γt

(2Re Σ Lu, u +2ReΣ Pu,u

+ 

dΣ

u, u−2γ Σ u, u)

for all γ. Then, integrating on R and estimating all terms by the Cauchy–Schwarz

inequality, we obtain a constant C

(depending on α and bounds for Σ, dΣ/dt

and Re (ΣP )) such that



−2γt

u(t)

))

dt ≤ C



−2γt

u(t)

)

+ C





−2γt

u(t)

))



1/2





−2γt

Lu(t)

)



1/2

for all γ>0. This implies that



−2γt

u(t)

)

dt ≤ C



(1 + εγ)



−2γt

u(t)

)

4εγ



−2γt

Lu(t)

)



for any ε>0. Choosing for instance ε =1/(3C

) yields the desired estimate

with γ

=3C

and C =3C

/2. 

This page intentionally left blank

PART II

THE LINEAR INITIAL BOUNDARY

VALUE PROBLEM

This page intentionally left blank