Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

13 Unconventional Superconductivity in Novel Materials 651

then decrease, according to the theory of MHZ [55].

However,at the highest pressures,such large values of

are required (∼ 10

K!) that it was concluded that

the Ce 4f -state must demagnetize within the context

of the Friedel–Anderson model.

An example of the second case is provided by

the La

1−x

system when Th is substituted for

La. With increasing Th concentration y in the

(La

1−y

)

1−x

system, the rate of the initial de-

pression of T

with Ce concentration passes through

a pronounced maximum and T

vs n changes con-

tinuously from curves with negative curvature and

reentrant behavior to curves with positive curvature

and exponential-like shapes [41]. Concomitantly, the

normal state magnetic susceptibility [57] and elec-

trical resistivity [58] evolve continuously from mag-

netic to nonmagnetic behavior.Aselfconsistent anal-

ysis of the rates of the initial depression of T

with n

and the value of the specific heat jump at T

demon-

strated thatthe MHZ theory provides a good descrip-

tion of the data from T

≈ 0.1 to 100 [59,60].

Magnetically-Ordered Superconductors

The series of isostructural ternary rare earth com-

pounds that have been investigated the most ex-

tensively in connection with the interaction be-

tween superconductivity and long-range magnetic

order include the rhombohedral rare earth molybde-

num chalcogenides RMo

and RMo

(Chevrel

phases), and the tetragonal rare earth rhodium

boridesRRh

[7,8].Thelong-range magnetic order

that many of these compounds exhibit can be traced

in part to the ordered R sublattice. The persistence of

superconductivity, even in the presence of relatively

large concentrations of R ions, can be attributed to

the relatively weak exchange interaction between the

conduction electron spins and the R magnetic mo-

ments. This, in turn, appears to be associated with

transition metal molecular units or “clusters” which,

along with the R ions, are the basic building blocks

of these ternary R phases. The superconductivity is

believed to be primarily associated with the tran-

sition metal d-electrons that are relatively confined

within the clusters and thereby interact only weakly

with the R ions. Equation 13.13 has been used to esti-

mate the magnitude of J for the RRh

compounds

from the depression of T

of LuRh

by R impuri-

ties with partially-filled 4f electron shells [61]. The

initial depression of T

of LuRh

by Gd impurities,

(dT

/dn)

n=0

= −19 K per atomicfractionof Gd inLu,

yields the value |J | =2.3 × 10

−2

eV-atom, assum-

ing N(E

)=0.35 states/eV-atom-spin direction [61].

Other ternary R compounds have been investigated

such as RRh

1.1

3.5

,RRuB

,etc.[7,8].

Antiferromagnetic Superconductors

The coexistence ofsuperconductivity andlong-range

antiferromagnetic order was discovered in the latter

part of the 1970s in the R molybdenum selenides

RMo

(R = Gd, Tb, and Er) [8,64] and R rhodium

borides RRh

(R = Nd, Sm and Tm) [8, 65] at the

University of California, San Diego, and in the R

molybdenum sulfides RMo

(R = Gd, Tb, Dy and

Er)[8,62] attheUniversityof Geneva.Theoccurrence

of antiferromagnetic ordering of the R magnetic mo-

ments in thesuperconducting state was inferredfrom

a -typeanomalyintheheatcapacityandacusp

in the magnetic susceptibility for the RMo

com-

pounds[8,64],andfrom afeaturein theupper critical

field H

vs temperature T curve in the RMo

com-

pounds [8,62].Neutron diffraction measurements on

GdMo

[66] and RMo

compounds with R = Gd,

Tb,and Dy [67] confirmed the antiferromagnetic or-

dering of the sublatticeof R ionsin the Chevrelphase

structure. The magnetic structure consists of alter-

nating ferromagnetic [100] planes in the nearly cubic

R sublattice in which the magnetic moments are par-

allel or antiparallel to the rhombohedral [111] axis.

Plots of the sublattice magnetization vs temperature

for RMo

compounds with R = Gd, Tb,and Dy are

shown in Fig. 13.11 where they are compared with

data for H

vs temperature displayed in the inset of

the figure [63]. There is a clear correlation between

the onset of the sublattice magnetization and the de-

pression of the H

curve below T

The anomalous depression of H

in the vicin-

ity of T

and other properties of antiferromagnetic

superconductors have been addressed by numerous

theories [68].Several mechanisms by means of which

superconductivityis modified by antiferromagnetic

652 M.B. Maple et al.

Fig. 13.11. Temperature dependence of the sublattice mag-

netization for RMo

compounds with R = Gd, Tb, and

Dy. The inset shows the measured upper critical field

(T) [62],after [63]

order have been considered. These include: (i) Re-

duction in pair breaking due to the decrease in the

mean magnetization and, in turn, the conduction

electron spin polarization below T

. (ii) Increase in

pair breaking due to magnetic moment ﬂuctuations

in the vicinity of T

. (iii) Decrease of the attractive

phonon mediated electron–electron pairing interac-

tion by antiferromagnetic magnons. (iv) Reduction

of the available phase space for virtual pair scattering

by the change in lattice periodicity associated with

antiferromagnetic order.(v)Pairingofelectronswith

finite momentum. Finite momentum pairing of elec-

trons in states (k, ↑; k + Q, ↓), where Q corresponds

to translation by a reciprocal lattice vector, was orig-

inally proposed by Baltensperger and Strassler [69]

in 1963,and has been incorporated into several sub-

sequent theories [68].

It should be emphasized that there are some an-

tiferromagnetic superconductorswhere H

actually

increases below T

,or, in other words, superconduc-

tivity seems to be enhanced below T

.Anotableex-

ample is the compound SmRh

whose resistively

determined H

vs T curve, shown in Fig. 13.12, ex-

hibits a sharp break in slope at T

= 0.87 K [9].

In contrast, the H

vs T curves of the other two

RRh

antiferromagnetic superconductors shown

in Fig.13.12 display differentbehaviors with decreas-

ing temperature; for NdRh

, which undergoes two

antiferromagnetic transitions at T

=1.31Kand

=0.89K,H

decreases abruptly at T

and then

increases sharply at T

, whereas for TmRh

, H

hardly changes at T

= 0.4 K [9]. Neutron diffrac-

tion experiments indicate that the magnetic phases

of NdRh

in zero magnetic field are body-centered

antiferromagnetic structuresin which the Nd

mo-

Fig. 13.12. Resistively determined upper critical

field H

vs temperature T for polycrystalline

samples of NdRh

,SmRh

,ErRh

,and

TmR h

,after[9]

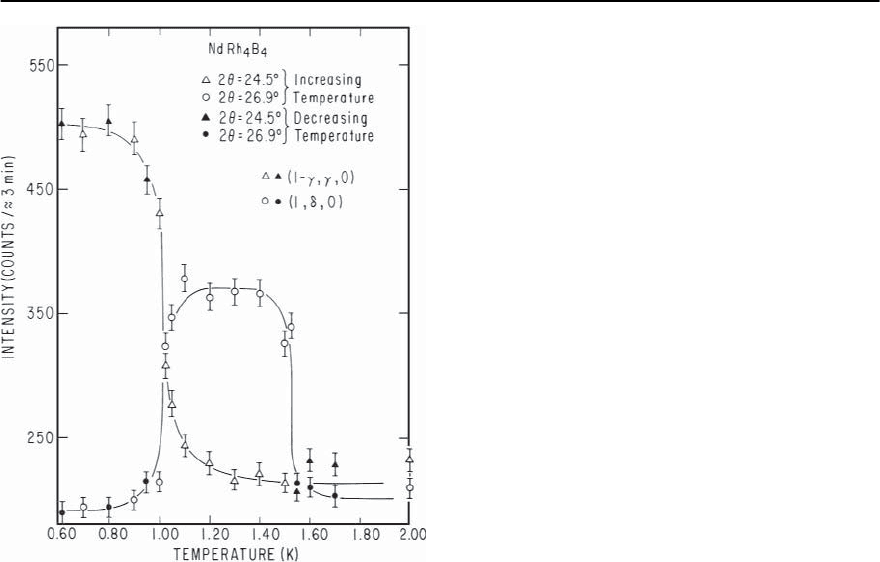
13 Unconventional Superconductivity in Novel Materials 653

Fig. 13.13. Temperature dependence of the neutron scatter-

ing intensity of a representative satellite from each of the

two magnetic phases of NdRh

, after [70]

ments are alternately aligned parallel and antiparal-

lel to the c -axis, with a sinusoidal modulation along

the [100] direction with  = 46.5 Å in the high tem-

perature phase, and along the [110] direction with 

= 45.2 Å in the low temperature magnetic phase [70].

The temperature dependences of theneutron diffrac-

tion intensity of a representative satellite from each

of the two magnetic phases of NdRh

are shown

in Fig.13.13.The data in Fig.13.12 indicate that there

is no universal behavior of H

vs T for antiferro-

magnetic superconductors. Both enhancements and

depressions of H

are found below T

,which appear

to be determined by a combination of the mecha-

nisms enumerated above.

Recently,superconductivity was discoveredin rare

earth transition metal borocarbide quaternary sys-

tems [71–73]. For intermetallic compounds, these

materials have high values of T

; T

≈ 13.5 K for

YNi

0.2

[71], T

≈ 16.5 K for RNi

C(R=Y,Tm,

Er, Ho, La) [72], and T

≈ 23 K for YPd

0.3

[73].

AvalueT

≈ 21.5 K was reported for a Th based pal-

ladium borocarbide in the Th-Pd-B-C system which

also has a relatively high extrapolated upper criti-

cal field H

(0) > 17 tesla [74]. Coexistence of su-

perconductivity and antiferromagnetism has been

reported in RNi

C for R = Tm, Er, Ho, Dy [75].

Single crystals of RNi

C compounds have been

prepared and investigated extensively by means of

a variety of experimental techniques [76–79].For ex-

ample,Grigereit and coworkers [78] have performed

neutron scattering measurements on the reentrant

antiferromagnetic superconductor HoNi

Cwhich

becomes superconducting at ∼ 7.5 K, re-enters the

normal conducting state at 5 K, and quickly recov-

ers superconductivity at lower temperature. The ex-

periments reveal that the magnetic order that first

forms upon cooling is oscillatory in nature and is

directly coupled to the superconducting order pa-

rameter. However, in contrast to the ferromagnetic

superconductors (discussed below), the oscillatory

state in HoNi

C is detrimental to superconductiv-

ity, and the superconducting state only survives at

low temperatures because of a first order transition

to a compensated antiferromagnet.A brief review of

the phenomena that arise from the interplay between

superconductivity and magnetism in the RNi

compounds can be found in [79].

Ferromagnetic Superconductors

Reentrantsuperconductivity dueto theonsetoflong-

range ferromagnetic ordering of the R magnetic

moments was discovered in 1977 in ErRh

[80]

at the University of California, San Diego, and in

HoMo

[81] at the University of Geneva. These

two materials, which become superconducting at an

upper critical temperature T

, lose their supercon-

ductivity at a lower critical temperature T

≈ T

where T

is the Curie temperature.Thermal hystere-

sis in various physical properties and a spike-shaped

feature in the heat capacity near T

indicate that a

first-order transition from the superconducting to

the ferromagnetic normal state occurs at T

[9].

Typical ac magnetic susceptibility and electrical

resistance vs temperature data for ErRh

are dis-

played in Fig. 13.14 [82]. The thermal hysteresis at

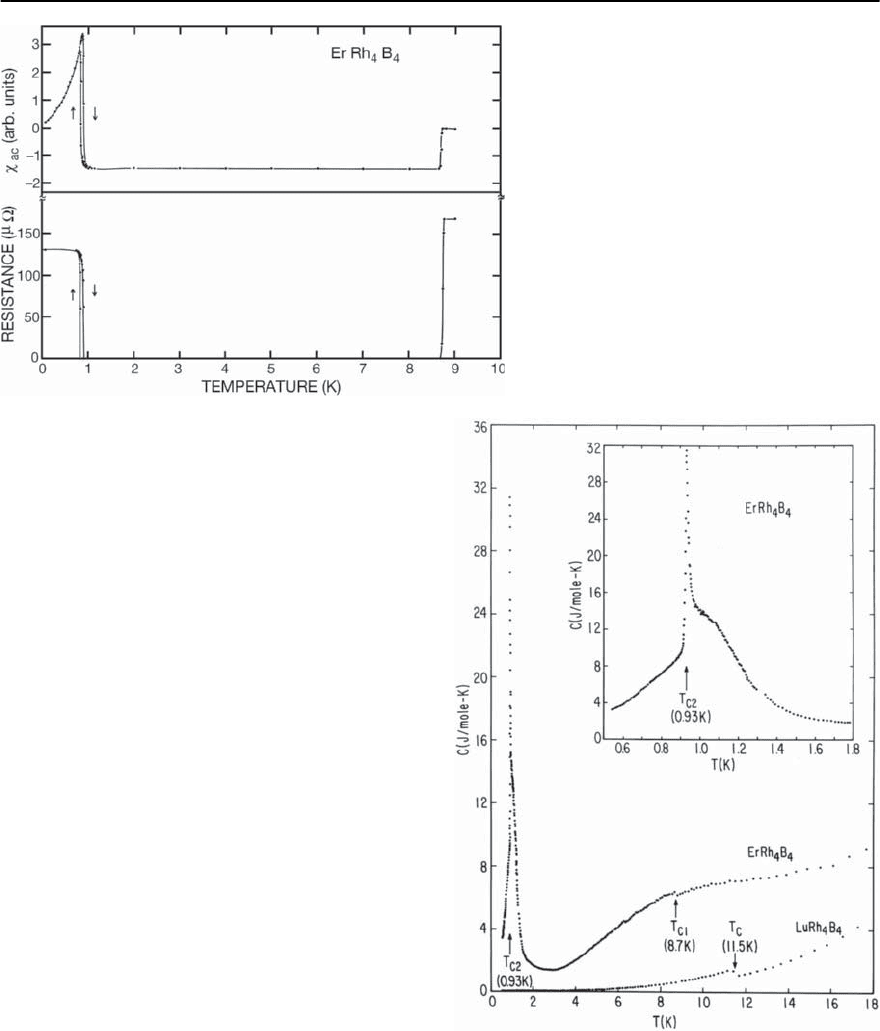
654 M.B. Maple et al.

Fig. 13.14. Typical ac magnetic susceptibility 

and electrical resistance vs temperature data for

ErRh

, after [82]

is evident in both properties. The resistively de-

termined H

vs T curve for ErRh

is shown in

Fig. 13.12 [9].

Neutron diffraction measurements established

that the groundstatesof thecompounds ErRh

[83,

84]andHoMo

[85] are ferromagnetic.In addition,

small angle scattering studies of ErRh

[84,86]and

HoMo

[87] revealed the existence of asinusoidally

modulated magnetic state with a wavelength of the

order of 100 Å that coexists with superconductivity

in a narrow temperature interval above T

.More-

over, in ErRh

the regions within which supercon-

ductivity and the sinusoidally modulated magnetic

state coexist appear to be interspersed with normal

ferromagnetic domains to form a spatially inhomo-

geneous state.

Shown in Fig. 13.15 is a plot of the heat capacity

of ErRh

and the isostructural nonmagnetic com-

pound LuRh

below 18 K [88]. The data reveal a

jump in the heat capacity at T

=8.7Konabroad

background with negative curvature that is a Schot-

tky anomaly arising from the partial lifting by the

CEF of the 16-fold degeneracy of the Er

J =15/2

Hund’s rule multiplet.At lower temperatures (see in-

set), there is a spike-shaped feature at T

=0.93

K (measured upon warming) superimposed on an-

other anomaly that is apparently associated with the

long-range ferromagnetic ordering of the Er

mag-

netic moments in the vicinity of T

[67]. There is

Fig. 13.15. Specific heat C vs temperature T for ErRh

and LuRh

.Theinset shows a detailed plot of C vs T for

ErRh

in the vicinity of the reentrant superconducting

transition at T

, after [88]

13 Unconventional Superconductivity in Novel Materials 655

Fig. 13.16. Small angle neutron scattering re-

sults on ErRh

obtained at various temper-

atures. The peak at 2 =1.4

◦

indicates an os-

cillatory magnetization with a wavelength of

100 Å, after [84]

also a shoulder in the heat capacity above T

whose

originmay be attributableto the formationof a sinu-

soidally modulated magnetic state that coexists with

superconductivity that is discussed below.

Measurements of the normalized neutron scatter-

ing intensity of the [101] reﬂection for ErRh

[84]

indicate that the ferromagnetic transition is broad,

extending up to ∼ 1.4 K, well above the tempera-

ture of the reentrant superconducting transition at

∼ 0.9 K. Also, there is definite thermal hystere-

sis between ∼ 0.8Kand∼ 1.4 K. The width of the

ferromagnetictransition hasbeen attributed toa dis-

tribution of effective Curie temperatures within the

material, while the hysteresis may be caused by the

nucleation of normal-ferromagnetic domains within

the temperature intervall between T

and ∼ 1.4K.

The heat capacity data also reveal thermal hysteresis,

part of which appears to be associated with the for-

mation of ferromagnetic domains (between ∼ 0.9K

and ∼ 1.3 K), and part of which is due to the reen-

trant transition at T

Neutron intensity vs scattering angle data at vari-

ous temperatures on a polycrystalline ErRh

sam-

ple, whose reentrant superconducting transition oc-

curs at ∼ 0.7 K, revealed the development of a peak

near 1

◦

which grows in intensity as the temperature

is decreased and then disappears abruptly when the

sample becomes normal below T

(see Fig. 13.16).

The data were interpreted in terms of ﬂuctuations

into astateinwhich the magnetizationis sinusoidally

modulated with a wavelength  ∼ 100 Å that was

assumed to take the form of a spiral. Subsequently,

neutron scattering experiments on an ErRh

sin-

gle crystal were performed by Sinha et al. [86]. Their

findings are consistent with the neutron scattering

experiments on polycrystalline ErRh

by Monc-

ton et al. [84], but revealed that the sinusoidally-

modulated magnetic state is a transverse linearly po-

larized long-range magnetic state with a wavelength

of ∼ 100 Å. The linearly polarized sinusoidal mod-

ulation lies along the [010] axis and the propaga-

tion directions are at 45

◦

to the [001] and the [100]

axes.The neutron scattering measurements on a sin-

gle crystal of ErRh

are summarized in Fig. 13.17.

NeutrondiffractionexperimentsonaHoMo

single crystal by Rossat–Mignod et al. [89] revealed

that the wavelength of the sinusoidally modulated

phase is twice as large as observed in powdered spec-

imens and is transverse, with the moments oriented

along the [111] direction while the wave vector is

along the [110] direction.The large value ofthe wave-

length ( ∼ 570 Å at 0.1 K) and the existence of a

ferromagnetic phase in microdomains of the order

of 1000 Å to 1500 Å were taken as evidence that the

modulated phase is actually induced by the electro-

magnetic interaction between the persistent current

and the magnetic moments.

656 M.B. Maple et al.

Fig. 13.17. Temperature dependence of the ferromagnetic

intensity from the (101) Bragg peak, the satellite intensity,

the dc resistance of ErRh

and the ratio of the satellite to

the ferromagnetic intensity for the (101) reciprocal lattice

point, after [86]

The sinusoidally modulated magnetic state that

coexists with superconductivity in HoMo

and

ErRh

is reminiscent of the cryptoferromagnetic

state proposed by Anderson and Suhl [90] in 1959

and has been the subject of much theoretical inter-

est during the late 1970s and early 1980s. Whereas

the original theory of Anderson and Suhl is based

on the exchange interaction, more recent theories

such as those of Blount and Varma [91], Ferrell et

al. [92], and Matsumoto et al. [93] are based on the

electromagnetic interaction. Although, as discussed

earlier, the exchange interaction is operative in these

materials, the electromagnetic interaction appears to

be primarily responsible for the sinusoidally mod-

ulated magnetic state that coexists with supercon-

ductivity. Other possibilities for the periodic mag-

netic structure above T

that have been considered

are (i) a spontaneous vortex lattice, (ii) a laminar

structure, stabilized by the R magnetization in a self-

consistent manner, and (iii) combined spiral mag-

netic and spontaneous vortex states [68].

Many other techniques have been applied to in-

vestigate the physical properties of HoMo

and

ErRh

,and the reader is referred to several reviews

on this subject that can be found in [8].

Superconductivity and Competing Magnetic

Interactions

Experiments on pseudoternary R compounds pro-

vide an alternative method for studying the inter-

action between superconductivity and long-range

magnetic order, as well as for exploring the effects

of competing types of magnetic moment anisotropy

and/or magnetic order. Two types of RRh

pseu-

doternarieshave been formed,one in whicha second

R element is substituted at the R sites, and another

in which a different transition element is substituted

at the Rh sites.

An example of the first type of pseudoternary

RRh

system is (Er

1−x

)Rh

whose low tem-

perature phase diagram, delineating the paramag-

netic, superconducting, and magnetically ordered

phases, is shown in Fig. 13.18. The phase bound-

aries have been determined from ac magnetic sus-

ceptibility [94,95] and neutron diffraction measure-

ments [96]. The phase diagram displays regions in

which the Er

and Ho

magnetic moments inde-

pendently order ferromagnetically within the basal

plane and along the tetragonal c-axis, respectively,

separated by a region of mixed magnetic phases. The

temperature interval above T

within which the si-

nusoidally modulated magnetic phase in ErRh

13 Unconventional Superconductivity in Novel Materials 657

Fig. 13.18. Low temperature phase diagram for the

(Er

1−x

)Rh

pseudoternary system, after [94–96]

coexists with normal ferromagnetic domains is also

indicated in Fig. 13.18. This inhomogeneous phase

presumably persists within a certain region in the

T − x plane (shaded area in the figure). There is a tri-

critical point at the concentration x

=0.89atwhich

andT

becomecoincident.TheT

vsx phase

boundary for x < x

is depressed relative to a linear

extrapolation of T

vs x for x > x

(dashed curve in

Fig. 13.18). Analysis of neutron diffraction data on

an (Er

0.4

0.6

)Rh

sample [97] indicates that the

actual T

of 3.67 K is about 0.2 K less than it would

have been in the absence of superconductivity, inac-

cord with the dashed-line extrapolation as well as

theoretical predictions.

A striking example of the second type of pseu-

doternary RRh

system is Ho(Rh

1−x

)

.This

system was first investigated by Ku et al. [99] and

provided evidence for the coexistence of supercon-

ductivity and antiferromagnetic order with T

> T

for x > 0.6. Subsequently, several detailed investi-

gations of a Ho(Rh

0.3

0.7

)

compound were car-

ried out; heat capacity measurements [88] confirmed

the bulk character of the antiferromagnetic order

in this material, while neutron diffraction experi-

ments [100] revealedthe magnetic structure.The low

temperature phase diagram of the Ho(Rh

1−x

)

system [94, 98], based on low temperature specific

heat, ac magnetic susceptibility,and electrical resis-

Fig. 13.19. Low temperature phase diagram for the

Ho(Rh

1−x

)

pseudoternary system, after [94,98]

tance measurements, is shown in Fig. 13.19. The first

study of this system yielded a similar phase diagram,

but with no evidence for magnetic ordering at tem-

peratures T > 1.2 K for 0.2 < x < 0.6.

Several other pseudoternary RRh

systems have

been investigated, and the reader is referred to more

comprehensive reviews for discussion and refer-

ences [8,13].

13.2.4 Magnetic Field Induced Superconductivity

One of the most dramatic manifestations of the inter-

action between superconductivity and magnetism is

the induction of superconductivity through the ap-

plication of a high magnetic field. The mechanism

that is apparently responsible for this phenomenon,

referred to as the exchange field compensation ef-

fect, was proposed by Jaccarino and Peter [4] more

than 20 years before magnetic field induced super-

conductivity (MFIS) was firmly established experi-

mentally [101].

The best example of MFIS is illustrated in

Fig. 13.20 which shows H

vs T for the compound

0.75

0.25

7.2

0.8

,taken from the work of Meul

et al. [101]. The normalized electrical resistance

(R/R

) vs applied magnetic field H at several tem-

peratures is displayed in the inset of Fig. 13.20. At

the lowest temperature (0.37 K), the data reveal a se-

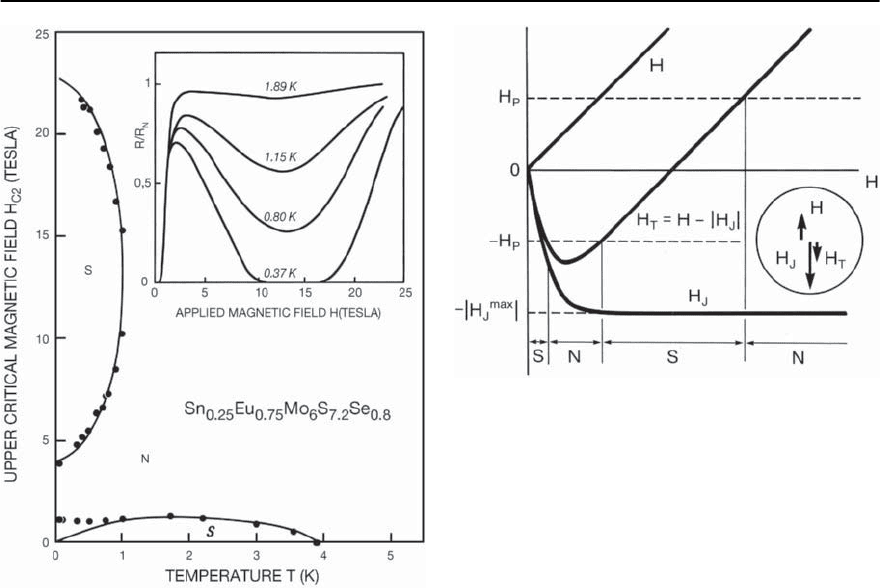
658 M.B. Maple et al.

Fig. 13.20. Magnetic field H − temperature T phase dia-

gram for the compound Eu

0.75

0.25

7.2

0.8

.Thesym-

bols S and N denote superconducting and normal regions,

respectively. The solid circles represent the H

(T)mea-

surements of Meul et al. [101], and the solid lines are the

boundaries predicted by theory. Normalized electrical re-

sistance R/R

, vs applied magnetic field data at several

temperatures are shown in the inset,after [101]

quence of transitions with increasing magnetic field

H from superconducting to normal, to supercon-

ducting again, and, finally, back to normal (S–N–S–

N). From a series of measurements of R/R

vs H at

various temperatures,the phase diagram in the H −T

plane was constructed (Fig. 13.20); two separate do-

mains of superconductivity are found, one at low

fields and another at high fields, whereas only one

domain of superconductivity at low fields is present

for a conventional superconductor.

MFIS occurs in type II superconductors in which

(T) is determined by the paramagnetic limiting

field H

and which contain magnetic moments that

are antiferromagnetically coupled to the spins of the

Fig. 13.21. Schematic diagram of the S–N–S–N transition

sequence in an applied magnetic field H.H

is the net mag-

netic field acting on the conduction electron spins,H

is the

exchange field produced by localized magnetic moments,

and H

is the paramagnetic limiting field. The material is

superconducting (S) when |H

| < H

and normal (N) when

| > H

, after [11]

conduction electrons. The magnetic moments in the

1−x

8−y

compounds are carried by the

divalent Eu ions and their coupling to the conduc-

tion electron spins generates an “effective” magnetic

field, the exchange field H

, that acts on the conduc-

tion electron spins in the same manner as an applied

magnetic field.If the sign of the coupling between the

Eu magnetic moments and the conduction electron

spins is negative, the direction of H will be opposite

to that of H

; i.e., the effect of H

will be “compen-

sated” by H (see inset of Fig. 13.21). The net mag-

netic field H

is then given by H

= H − |H

|.The

sequence of S–N–S–N transitions shown in the inset

of Fig.13.20 can be explainedin termsof therelation-

ship between H

and H

as illustrated schematically

in Fig. 13.21 [11]. The upper and lower curves show

the applied field H and the exchange field H

,respec-

tively, the sum of which yields the net magnetic field

.ThevariationofH

with respect to the value of

H determines the superconducting behavior of the

material.

In zero applied field, the compound is supercon-

ducting. As the applied magnetic field is increased,

the Eu magnetic moments become aligned in the di-

13 Unconventional Superconductivity in Novel Materials 659

rection of the field at a relatively low H-value and

| attains its maximum value |J

max

| of 30–50 tesla.

Consequently, provided |H

| is greater than H

,the

magnitude of H

(which is now negative) can become

larger than H

and drive the material into the nor-

mal state. As the applied magnetic field is increased

further, the net magnetic field starts to decrease in

magnitude, until its magnitude falls below H

when

the compound once more becomes superconducting.

Thereafter, H

increases linearly with H,vanishing

and then changing sign at H = |H

max

| where H

completely compensated, until H

(now positive) ex-

ceeds H

, when the system once again becomes nor-

mal. Because the value of the exchange field can be

rather large, the compensation effect can take place

at very high magnetic fields.

In actuality,the second transition from supercon-

ductivity to the normal state will also occur if H

surpasses the orbital critical field H

∗

of the com-

pound. Thus, in order to observe MFIS, it is impor-

tant that H

∗

, which can also limit the value of the

upper critical field H

, is large enough to allow su-

perconductivity to occur in this magnetic field range

(that is,H

∗

> |H

max

| − H

), since the orbital effects

are not compensated by the Jaccarino–Peter mecha-

nism. The compensation of the exchange field by the

applied magnetic field in several Eu

1−x

sys-

tems (where M is a metal such as Sn, Pb, La [102] or

Yb [103]) and in EuMo

under pressure [104], had

been inferred from an enhancement and anomalous

temperature dependence of H

in these materials.

Following the initial suggestion by Jaccarino and

Peter that MFIS could occur in a ferromagnet due to

exchange field compensation, several theoretical in-

vestigations of MFIS in paramagnetic systems were

carried out [105–107].One model, based on the the-

ory of type II superconductivity including the ef-

fect of the exchange field [106], was used by Meul

et al. to analyze their H

(T)measurementsonthe

1−x

system.The calculated boundaries of

the two superconducting domains observed for the

compound Eu

0.75

0.25

7.2

0.8

are indicated by

the solid lines in Fig. 13.20 where the parameters of

the theory have been adjusted to give the best fit to

thedata.TheexcellentdescriptionoftheH − T su-

perconducting phase boundaries shown in Fig. 13.20

is striking confirmation of the Jaccarino–Peter com-

pensation mechanism.Jaccarino and Peter originally

suggested MFIS in a weakly ferromagnetic material,

assuming that it would be superconducting in the

absence of ferromagnetic ordering. MFIS in a ferro-

magnet remains to be discovered.

13.3 f -Electron Heavy Fermion

Superconductors

13.3.1 Introduction

In heavy-fermion compounds, strong electronic in-

teractions between the conduction electrons and

the localized f -electrons of rare earth or actinide

ions result in large quasiparticle effective masses,

up to several hundred times the free-electron mass.

These compounds display a wide variety of strik-

ing correlated-electron phenomena including va-

lence ﬂuctuations, the Kondo effect, magnetic order,

non-Fermi liquidbehavior,and,of course,supercon-

ductivity.

As discussed in Sect. 13.2, magnetic moments in

conventional superconductors suppress and eventu-

ally destroy superconductivity with increasing con-

centration of magnetic ions. In fact, for decades it

was generally accepted that magnetism and super-

conductivity were inimical. Thus, the 1979 discov-

ery of superconductivity in the heavy-fermion com-

pound CeCu

[108], in which the sublattice of Ce

ions possess well-defined local moments at high tem-

peratures, posed a major puzzle to researchers. Since

then,the list of superconducting heavy-fermion com-

pounds has expanded to include about twenty Ce,

U, Pu, and Pr-based compounds. The known heavy

fermion f -electron superconductors and their crys-

tal structure and lattice parameters are listed in Ta-

ble 13.1.Many of these compounds display the coex-

istence of antiferromagnetism (AFM) and supercon-

ductivity, and, recently, ferromagnetic superconduc-

tors have been added to the list (UGe

[3], URhGe

[109]).

The study of superconductivity in heavy-fermion

compounds has led to a range of unexpected phe-

nomena and new theories. It is now widely suspected

that heavy-fermion superconductivity (HFSC) is

660 M.B. Maple et al.

Table 13.1.Crystal structure and lattice parameters of heavy-fermion superconductors

Compound Structure Type Lattice Parameters (Å) Ref.

abc

CeCu

ThCr

(Tetr. I4/mmm) 4.103 9.94 [110]

CePd

ThCr

(Tetr. I4/mmm) 4.24 9.88 [111]

CeRh

ThCr

(Tetr. I4/mmm) 4.09 10.18 [111]

CeNi

ThCr

(Tetr. I4/mmm) 4.150 9.854 [112]

CeCu

ThCr

(Tetr. I4/mmm) 4.18 10.18 [113]

CeIn

AuCu

(Cub. Pm3m) 4.689 [114]

CeRhIn

HoCoGa

(Tetr. P4/mmm) 4.652 7.542 [115]

CeIrIn

HoCoGa

(Tetr. P4/mmm) 4.668 7.515 [116]

CeCoIn

HoCoGa

(Tetr. P4/mmm) 4.62 7.56 [117]

RhIn

CoGa

(Tetr. P4/mmm) 4.665 12.244 [118]

CePt

Si CePt

B(Tetr.P4mm) 4.072 5.442 [119]

CeRhSi

BaNiSn

(Tetr. I4/mm) 4.269 9.738 [120]

CeIrSi

BaNiSn

(Tetr. I4/mm) 4.252 9.715 [120]

CeNiGe

SmNiGe

(Ortho. Cmmm) 21.808 4.135 4.168 [121]

(Ortho. Ibam) 9.809 11.838 5.960 [122]

PrOs

LaFe

(Cub. Im

3) 9.3017 [123]

UBe

NaZn

(Cub. Fm

3c) 10.268 [124]

UPt

SnNi

(Hex. P6

/mmc ) 5.764 4.899 [125]

URu

ThCr

(Tetr. I4/mmm) 4.121 9.681 [126]

UPd

PrNi

(Hex. P6/mmm) 5.365 4.186 [127]

UNi

PrNi

(Hex. P6/mmm) 5.207 4.018 [128]

UGe

ZrGa

(Orth. Cmmm) 4.036 14.928 4.116 [129]

UIr PdBi (Mono. P2

) 5.620 10.590 5.598 (ˇ =89.93

◦

) [130]

URhGe TiNiSi (Orth. Pnma) 6.855 4.327 7.501 [131]

Fe Mn

Fe (Tetr. I4/mcm) 10.302 5.239 [132]

PuCoGa

HoCoGa

(Tetr. P4/mmm) 4.232 6.786 [133]

PuRhGa

HoCoGa

(Tetr. P4/mmm) 4.301 6.857 [134]

magnetically mediated, with an unconventional su-

perconducting order parameter (p or d-wave sym-

metry) that vanishes at lines or points on the Fermi

surface. In UPt

and U

1−x

, multiple super-

conducting phases are observed which is evidence

for a complex, multicomponent superconducting

order parameter. Very recently, superconductivity

was discovered [123, 135] in PrOs

,inwhich

the superconductivity may be mediated by electric

quadrupolar interactions ratherthan magnetic inter-

actions of the Pr ions, suggesting a new mechanism

for superconductivity in heavy fermion systems. Two

decades later, the question of how superconductivity

and magnetism can coexist still remains a formidable

challenge and further research into this subject will

no doubt greatly expand our understanding of su-

perconductivity.

In this section, we brieﬂy review the normal and

superconducting properties of heavy-fermion super-

conductors, in general.We then focus on a few exem-

plary compounds such as the CeMIn

(M = Rh, Co,

Ir), UGe

,andPrOs

. The compound UPd