Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

3 Electron–Phonon Superconductivity 137
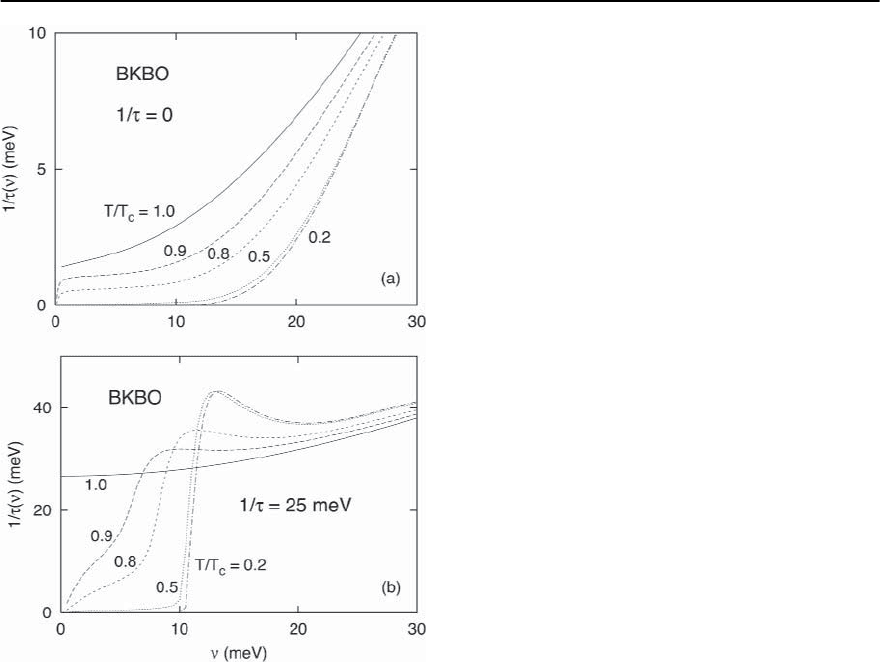
Fig. 3.53. The conductivity–derived scattering rate, 1/( )
vs. frequency in the s–wave superconducting state for (a)
1/ =0meVand(b)1/ = 25 meV, for temperatures as
indicated. In both cases we used the BKBO spectrum with
=1.In(a) there is no signature for a gap, while one
remains at low temperatures in (b)
since the phonon spectrum extends only to 80 meV.
More detailed comparisons with self-energy-derived
scatteringrateshavebeenprovided inRefs.[184,186].
The results shown in Fig. 3.51 were obtained in the
normal state. In the superconducting state the pres-
ence of a gap will modify the low frequency be-
haviour of the scattering rate, 1/( ). Results within
BCS theory (elastic scattering rate only — no inelas-
tic scattering) are shown in Fig. 3.52. At low frequen-
cies the overall scale of the effective scattering rate
is set by the elastic scattering rate (2 and 25 meV,
respectively). Note that in the gap region (below 32
meV) theeffectivescattering rateis zero (at zero tem-
perature), while slightly above the gap the effective
scattering rate below T
c
is actually enhanced with re-
spect to the normal state value. In Fig. 3.53 we show
the effective scattering rate vs. frequency using the
model Ba
1−x
K
x
BiO
3
spectrum in (a) the clean limit
and (b) with significant impurity scattering. The re-
sults are qualitatively similar to those in Fig.3.53.
3.6.4 Phonon Response
Much of this review has focused on various proper-
ties whose determination allows one to infer the de-
gree of electron–phonon coupling that exists in the
material under study.The majority of properties that
fall in thiscategory refer to a modification ofthe elec-
tronic structure or response due to a coupling with
phonons. To a much lesser extent the phonons them-
selves are modified because of the electron–phonon
coupling,and in this section we brieflyaddress a few
examples in this category.
The impact of the superconducting state on the
phonons was first investigated using ultrasound ex-
periments [324]. Sound waves are attenuated due to
their absorption in the solid.The absorption requires
interaction with electrons with energies very close
to the Fermi energy (the phonon energy is typically
very low for sound waves — in the 100MHz = 0.0004
meV range). These electron states are gapped in the
superconducting state,so the attenuation is expected
to be suppressed to zero as T → 0. The BCS re-
sult, given by Eq. (3.177), is valid for an order pa-
rameter with s-wave symmetry.A similar law can be
derived for other symmetry types, which results in
some sort of power law decay rather than exponen-
tial at low temperatures. (See, for example, a recent
paper which reports measurements on Sr
2
RuO
4
,and
references therein [325]. )
Of main interest here is how Eq. (3.177) is mod-
ified when retardation effects are accounted for. An
early calculation [326] found that retardation effects
didnotaltertheresultEq.(3.177).Therefore,little can
be learned about the electron–phonon interaction
through ultrasonic experiments; instead, one should
examine higher energy phonons.
The classic experiment of this type was performed
using neutron scattering on Nb and Nb
3
Sn [327].The
138 F. Marsiglio and J.P. Carbotte
idea is simply that the electron charge susceptibility
modifies the phonon spectrum. Within the normal
state this modification is hardly noticeable in met-
als over a temperature range of 300 K or so. How-
ever, when the material goes superconducting, the
electron density of states is profoundly modified at
energy scales of order the gap; this in turn will af-
fect phonons whose energy is on the same scale. In
particular, a low energy phonon (energy less than
2) that had a finite lifetime because it could decay
into an electron-hole pair will be unable to do so in
the superconducting state because no states exist at
energies below the gap, . Therefore its lifetime will
lengthen considerably in the superconducting state,
resulting in a narrower lineshape below T
c
.Figure
3.54 shows the experimental result from Nb
3
Sn [327]
where the lineshape has clearly become narrower in
the superconducting state. Similarly, if the phonon
energy is slightly above 2,then,under the right con-
ditions,the linewidth will increase,since the electron
density of states increases in this energy regime in
the superconducting state.
A detailed theory of these effects was first given
in [328], within BCS theory. The theory consists of
a calculation of a response function correspond-
ing to a Case I observable. Similar calculations
were performed much later by Zeyher and Zwick-
nagl [289] to understand the frequency shifts and
linewidth changes (due to superconductivity) in the
q = 0 Raman spectra for various optical modes in
YBaCu
3
O
7−X
.Theyfound,usingtheBCSapproxima-
tion,
Re ¢(q =0, + iı)
N(0)
= (3.182)
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
−
2
¯
√
1−
¯
2
tan
−1
¯
√
1−
¯
2
for
¯
< 1
1
¯
√
¯
2
−1
ln
2
¯
2
−1+2
¯
√
¯
2
−1
for
¯
> 1.
The imaginary part is given for all temperatures by:
Im ¢(q =0, + iı)
N(0)
=−(
¯
−1)
tanh ˇ/4
¯
√
¯
2
−1
,
(3.183)
where
¯
= /(2(T)). Here, ¢(q, + iı)isthe
change in the phonon self-energy between the su-
perconducting state and the normal state. A posi-
tive (negative) real part means that phonons harden
(soften) in the superconducting state,while a positive
(negative) imaginary part means that the phonon
linewidths narrow (broaden). Thus, phonons below
the gap edge (2) soften while those above harden.
Also, above the gap edge they broaden while be-
low their linewidth does not change.The broadening
above 2 can be understood as being due to the en-
hanced scattering with electrons, since the electron
density of states now has a square-root singularityin
the energy range of , and the phonon self-energy is
essentially a convolutionof two single electronGreen
functions (see Eq. (3.146)).
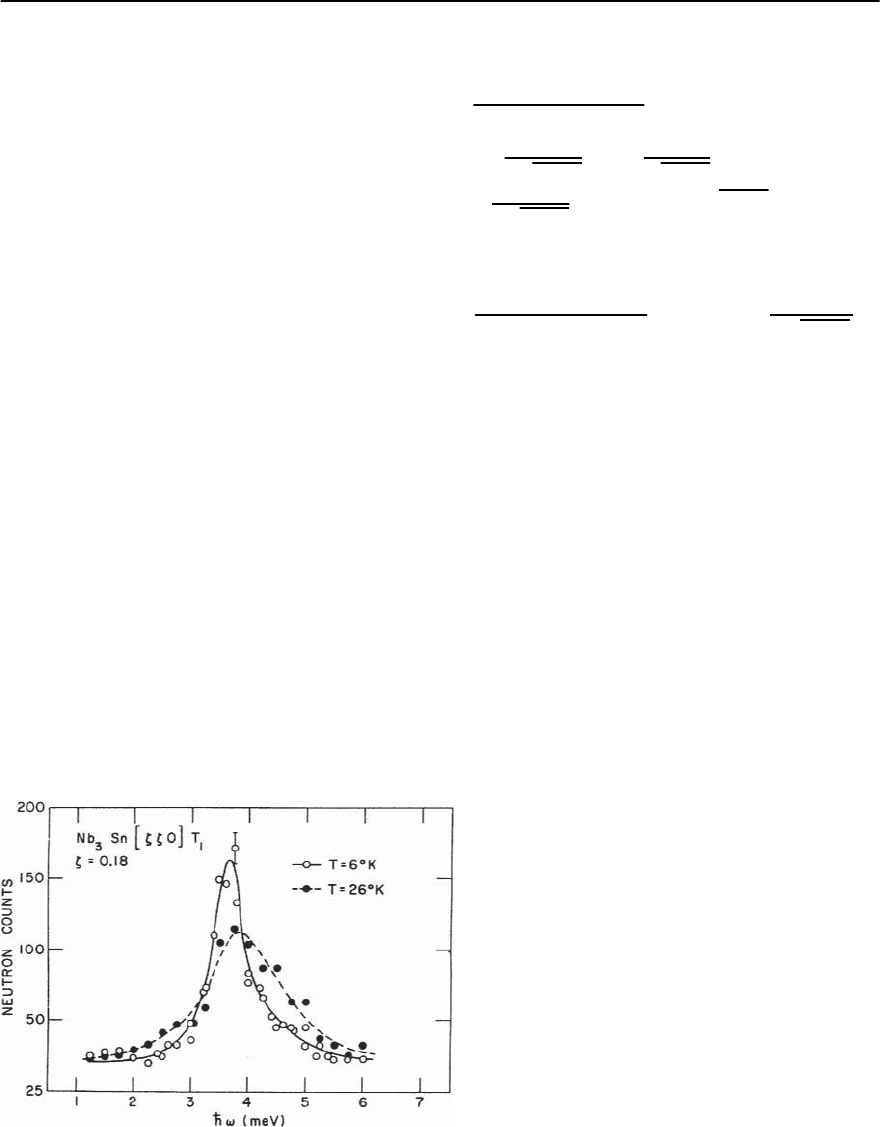
Fig. 3.54. The widths of low energy [0]T
1
acoustic
phonons broaden appreciably at temperatures above
T
c
, the superconducting transition temperature. This
figure shows the same phonon profile above and below
T
c
≈ 18.0 K Reproduced from [327]
3 Electron–Phonon Superconductivity 139
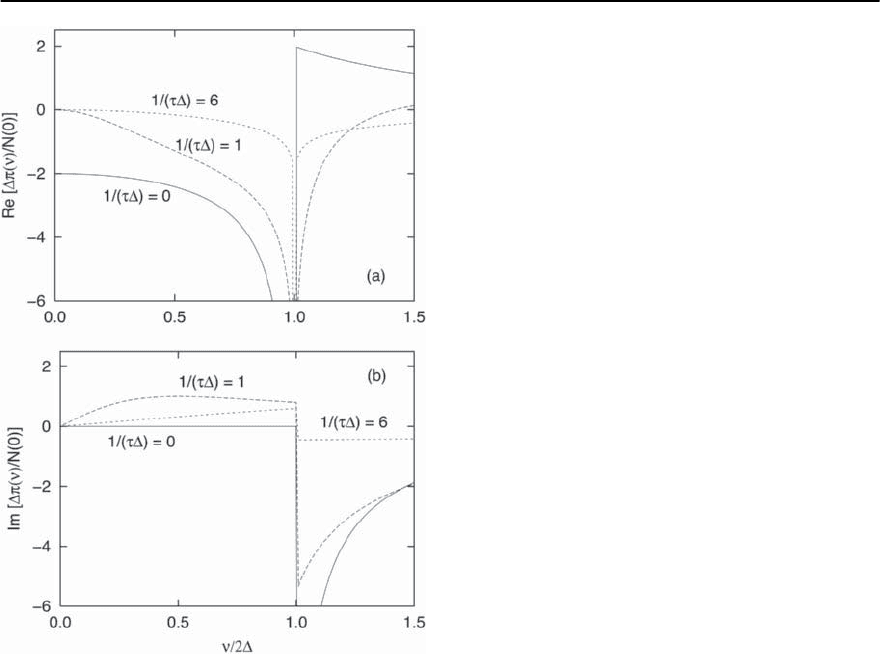
Fig. 3.55. (a)Realand(b) Imaginary part of ¢( + iı)/
N(0) vs /(2
0
) at zero temperature, for various impu-
rity scattering rates, 1/(
0
)=0(solid), 1 (dotted), and 6
(dashed), in the weak coupling (BCS) approximation. Be-
low twice the gap edge the phonons soften; above twice
the gap edge they harden in the clean limit and soften
in the dirty limit. Note the narrowing that occurs below
the gap edge in the presence of impurity scattering. Taken
from [290]
Eqs. (3.182, 3.183) have been derived assuming
single particle Green functions without impurity
scattering. The q = 0 limit is somewhat anoma-
lous in this case, in that the phonon width is already
zero in the normal state. Hence, no change can oc-
cur in the linewidth in the superconducting state,
for frequencies below 2.A calculation with impuri-
ties [290] provides a non-zero linewidth in the nor-
mal state. Because of the gap in the single electron
density of states in the superconducting state, this
linewidth is reduced to zero when the system en-
ters the superconducting state, so the change in the
imaginary part of the phonon self-energy is posi-
tive. These results are summarized in Fig. 3.55. Note
that the softening below the gap edge is significantly
reduced with impurity scattering present, and the
phonons above 2 also soften when a significant de-
gree of impurity scattering is present. As Fig. 3.55b
shows, phonons whose energy lies below 2 acquire
a narrower linewidth in the superconducting state,
as noted above.
The effects of retardation on the phonon self-
energy are not very significant. The changes that
do occur follow the changes already discussed due
to including elastic scattering; high energy phonons
soften rather than harden, and the broadening that
accompanies this softening is reduced compared to
the clean BCS case. More detailed changes are docu-
mented in Refs. [289,290].
Because these phonon changes can be observed
through neutron scattering experiments, it is of in-
terest to examine the phonon self energy at non-zero
momentum, q [291,292]. In this case the phonon has
a non-zero linewidth in the normal state, and so line
narrowing is observed in the superconducting state
at low frequencies,due to the development of a single
electron gap. The detailed frequency dependence is
a function of the band structure; in particular, with
two dimensional nesting phonon changes due to su-
perconductivity are enhanced [292].
3.7 Anisotropy and MgB
2
Arguably the most recent exciting discovery in su-
perconductivity is in MgB
2
with T
c
= 39 K [329].
This is a very simple binary compound, although
its structure leads to considerable anisotropy in the
superconductivity, which is why we combine these
two topics here. While preliminary analysis seemed
inconsistent with electron-phonon driven supercon-
ductivity [330–332],most researchers now appear to
believe that MgB
2
is an electron-phonon supercon-
ductor, albeit with somewhat unusual properties due
to the gap anisotropy and the multi-band structure
at the Fermi energy.An early review is [333]; a more
recent review appears to be lacking.
140 F. Marsiglio and J.P. Carbotte
We begin with a brief summary of Eliashberg the-
ory withanisotropy.We followthecommon approach
which confines electronic properties to the Fermi
surface, but accounts for multiple band and/or vari-
ations in coupling strength as one moves around the
Fermi surface(s). We begin with Eqs. (3.50), (3.51)
and (3.52) and adopt particle-hole symmetry so that
Eq. (3.51) is not required. By assuming that the mo-
mentum dependence of various quantities is impor-
tant only on the Fermi surface, one can perform the
energy integration to obtain
(k, i!
m
)=
'
T
m
k,k
(i!
m
− i!
m
)−
∗
k,k
×
(k
, i!
m
)
!
2
m
Z
2
(k
, i!
m
)+
2
(k
, i!
m
)
(
Z(k, i!
m
)=
1+
'
T
m
k,k
(i!
m
− i!
m
)
!
m
Z(k
, i!
m
)/!
m
!
2
m
Z
2
(k
, i!
m
)+
2
(k
, i!
m
)
(
, (3.184)
where the angular brackets denote an average over
all directions of k
on the Fermi surface. A pop-
ular model to describe the resulting anisotropy in
the interaction is the separable model first described
in [334],
F
k,k
=(1+a
k
)F(1 + a
k
), (3.185)
where F is any property, and the (small) quantity
a
k
has average zero over the Fermi surface (i.e.
< a
k
>= 0) but has a non-zero average to second or-
der,i.e.< a
2
k
>= a
2
,wherea is some small parameter.
In this way the precise functional form of a
k
is not
required, and everything is encapsulated in the pa-
rameter a
2
.In Eqs. (3.184) anisotropy arises through
˛
2
k,k
F(§) and the Coulomb pseudopotential,
∗
k,k
.
Following the reduction to a BCS-like model de-
scribed in an earlier section , we obtain
T
c
=1.13!
D
exp
−1
N()V (1 + a
2
)
, (3.186)
where V is the average (attractive) interaction on
the Fermi surface. Note the additional factor of
(1 + a
2
) compared with Eq. (3.40). This indicates that
anisotropy increases the critical temperature.The or-
der parameter at zero temperature,
k
(0) varies as
1+a
k
;oneobtains
2 <
k
(0) >
k
B
T
c
=3.53
1−
3
2
a
2
, (3.187)
so anisotropy reduces the value of this ’universal’ ra-
tio.Many other properties can be found in [335]. For
example, the critical magnetic field at zero tempera-
ture, H
c
(0), is given by
H
2
c
(0)
8
=
1
2
N() <
k
(0) >
2
(1 + a
2
) , (3.188)
while the specific heat jump is given by
C(T
c
)
T
c
=1.43(1 − 4a
2
) , (3.189)
and is clearly reduced from its BCS value. For tem-
peratures near T
c
,weobtain
<
k
(T) >
<
k
(0) >
=
1.74(1 − a
2
)
√
1−t[1 − (0.41 − 1.36a
2
)(1 − t)] ,
(3.190)
to order (1−t)
3/2
(t ≡ T/T
c
) so that the temperature
dependence of the BCS order parameter is modi-
fied from its isotropic dependence (see Fig. 3.33, top
frame). Finally, to order (1 − t) the specific heat be-
comes
C(T)
T
c
=2.43(1 − 2.35a
2
)−4.76(1 − 4.79a
2
)[1 − t] .
(3.191)
At low temperatures we obtain the reduced critical
magnetic field
h
c
(t) ≡
H
c
(T)
H
c
(0)
=1−1.06t
2
(1 + 2a
2
)−0.56t
4
(1 + 4a
2
)
(3.192)
and the deviation function Eq. (3.140)
D(t)=−(0.06+2.11a
2
)t
2
−0.56t
4
(1+4a
2
) . (3.193)
3 Electron–Phonon Superconductivity 141
Even within the separable anisotropy model one
can include more realistic modelling at the level
of the electron-phonon spectral function. Using
˛
2
k,k
F(§) ≡ (1 +b
k
)˛
2
F(§)(1 + b
k
),Zarate and Car-
botte [336] found to order b
2
T
c
=1.13!
D
e
(−
1+
−
∗
)
1+˛
2
(
1+
−
∗
)
, (3.194)
where
˛
2
≡ b
2
(1 +
∗
)
(1 + )( −
∗
)
2
. (3.195)
Equation (3.194) agrees with Eq. (3.186) with
−
∗
1+
playing the role of N()V and ˛
2
replacing a
2
.Note
that for a given value of b
2
the effective anisotropy
parameter ˛
2
is largest when is small, i.e. com-
parable to
∗
.Thisadditionalfeatureisuniqueto
Eliashberg theory, and is not present in BCS theory.
The expression for the average gap ratio is modified
in two ways. It is
2 <
k
(0) >
k
B
T
c
=3.53(1 −
3
2
+
−
∗
1+
˛
2
) . (3.196)
A comparison with Eq. (3.187) shows that (i) a
2
→
˛
2
and (ii) the factor 3/2 is increased within Eliash-
berg theory. These examples should suffice to make
it clear that Eliashberg calculations are required for
a quantitative analysis of anisotropy effects, even
within the separable model for anisotropy. Note,
however, that Eqs. (3.189)–(3.193) remain valid with
a
2
→ ˛
2
.
Daams and Carbotte [124] have obtained detailed
numerical results forproperties of an anisotropicsu-
perconductor based on the full Eliashberg equations
(3.184) with a separable model for ˛
2
k,k
F(§). The
isotropicpart was taken from tunneling experiments,
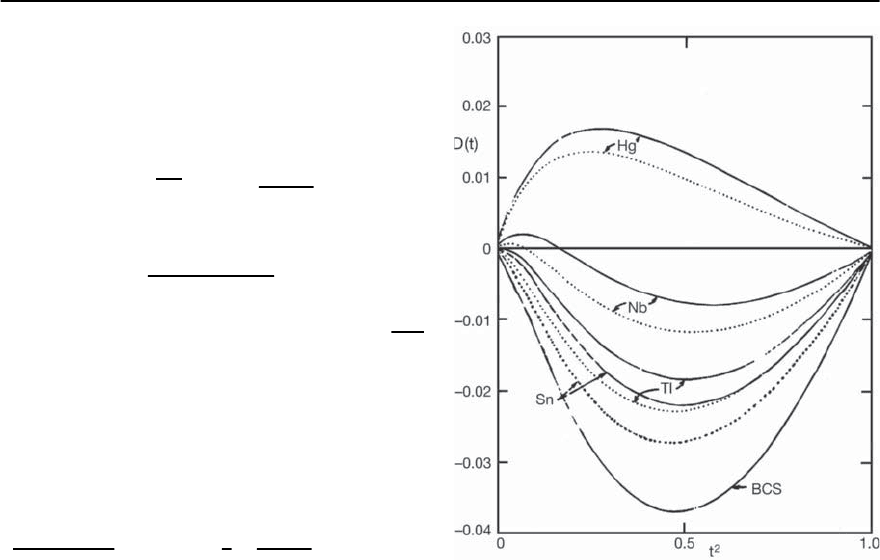
as described previously.Their results of D(t)vs.t
2
for
several materials are shown in Fig. 3.56. Solid curves
are the isotropic case while the dotted curves are for
b
2
=0.04 in all cases. Of course in real materials the
anisotropy may not be separable.
Normal impurity scattering can be included as in
Eqs. (3.153) and (3.154), with the appropriately gen-
eralized momentum dependent functions, although
in general the impurity scattering rate can be de-
pendent on momentum, as well, 1/ → 1/
k,k
.Here
Fig. 3.56. The deviation function D(t)vs.t
2
calculated from
Eliashberg theory for various elemental superconductors
with (dotted)andwithout(solid) anisotropy. From [124]
we assume this rate is independent of momentum.
Then,since impurity scattering tends to wash out gap
anisotropy, T
c
is reduced from its anisotropic pure
single crystal value [294],as is clear from Eq.(3.194),
for example. Thus, the so-called “dirty limit” is also
the isotropic limit. For small impurity content,T
c
de-
creases linearly with impurity scattering, with a co-
efficient proportional to the mean square anisotropy
a
2
in BCS theory. Within Eliashberg theory similar
results are achieved with a
2
→ ˛
2
[337].Ashraf and
Carbotte [338] show that the effect of impurities on
T
c
of an anisotropic BCS superconductor is qualita-
tively though not quantitatively correct.Full numer-
ical results are given in [124]. The effect of impuri-
ties on the thermodynamic properties within the
model are given in [339].
How large is the typical anisotropy in ˛
2
k
F(§)in
conventional superconductors? In Fig. 3.3 we showed
the directional dependence of the electron-phonon
spectral functioninAldeterminedthroughmultiple-
142 F. Marsiglio and J.P. Carbotte
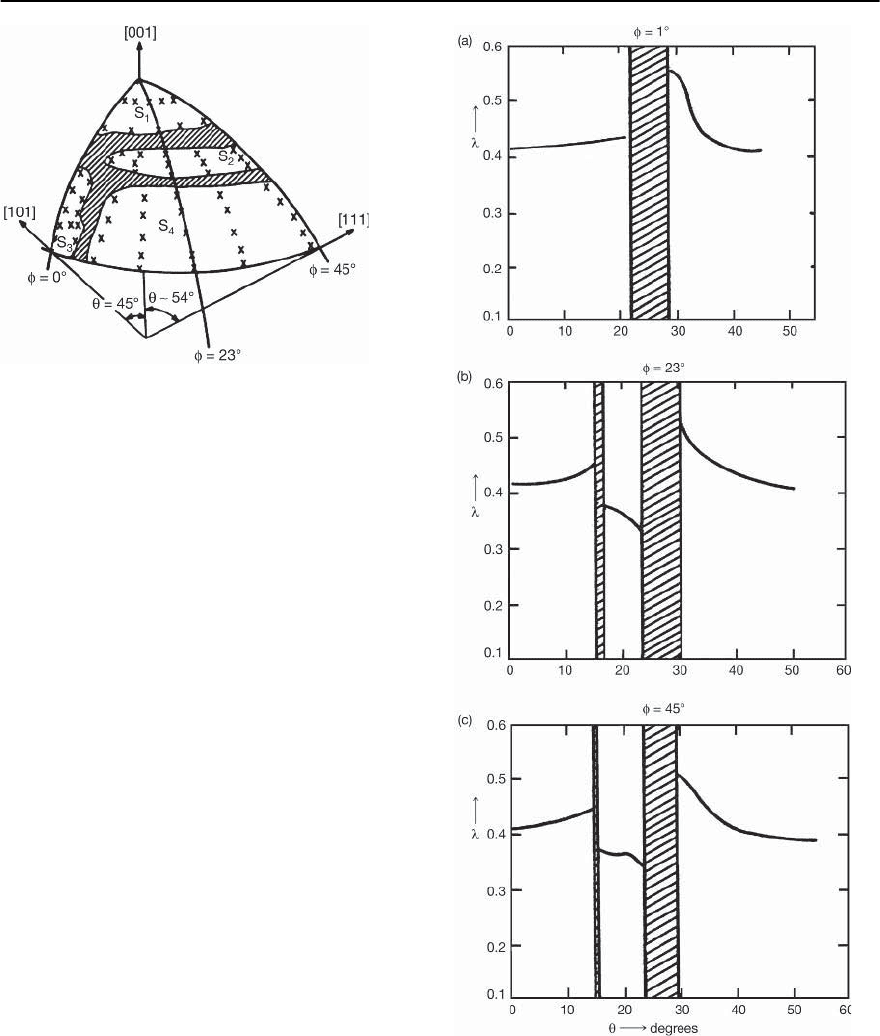
Fig. 3.57. A schematic diagram showing positions on the
real Fermi surface for Al at which calculations have been
performed.From [340]
plane-wave band structure calculations. In Fig. 3.57
we show a schematic representation of the 62 points
(X’s) at which calculations of ˛
2
k
F(§) were carried
out on the irreducible 1/48 of the realistic Fermi
surface of Al. The shaded region contains no free
states. To have a measure of the electron-phonon
anisotropy weexamine the mass renormalizationpa-
rameter
k
=2
∞
0
d§˛
2
k
F(§)/§; these are shown
in Fig. 3.58 [340]. Note the variations of order 30%.
Estimates of gap anisotropy based on this calculated
spectral function were provided in [340] and are re-
produced in Fig. 3.59. Again gap variations are con-
siderable; estimates are
that T
c
for a pure single crystal will be 9% higher
than the isotropic limit. Experiment gives about 5%.
Further details and similar calculations for Pb can be
found in [150,255].
Equations (3.184) along with impurity contribu-
tions can be used to treat an isotropic two-band
model, and has been done recently for MgB
2
.InEqs.
(3.184) the momentum sums in principle can sum
over band indices as well. Using this fact we can re-
gard these equations as appropriate to an isotropic
two band model, where only 2 indices are now re-
quired in the sum. Moreover, 4 discrete values of
˛
2
ij
F(§)withi , j =1, 2 are required.For the moment
we can regard the direct Coulomb repulsion,
∗
,and
the impurity scattering 1/, as isotropic quantities.
Fig. 3.58. The variation of
k
as a function of in planes
defined by = constant, calculated in the multiple-plane-
wave approximation. The shaded areas indicate Bragg
plane regions. From [340]
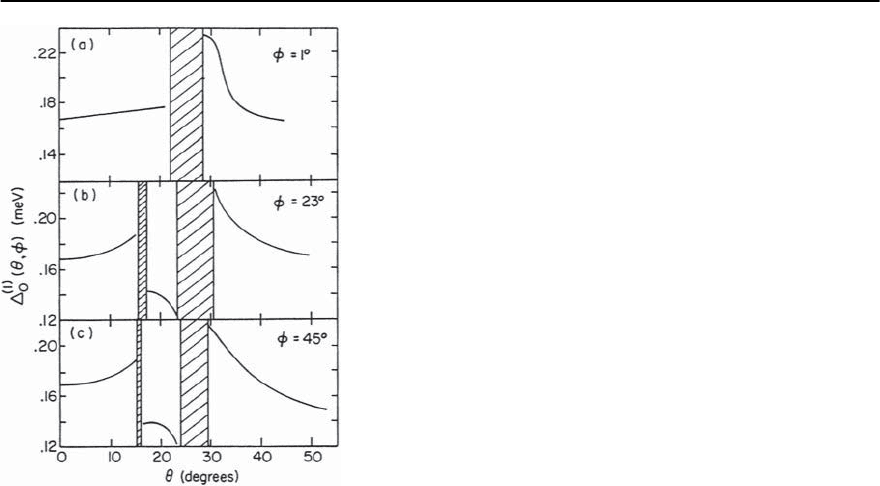
3 Electron–Phonon Superconductivity 143
Fig. 3.59. The variation of the gap function for three con-
stant arcs. The shaded ar eas indicate places where there
is no Fermi surface. From [340]
If desired, additional anisotropy within a band could
be modelled with a separable model.
InthecaseofMgB
2
Nicol and Carbotte [341] have
reviewed the data and arguments for the simplic-
ity of a minimal model to describe superconducting
properties. There is evidence that impurities mainly
provide intraband scattering in the case of MgB
2
.
But intraband scattering does not contribute to T
c
or to the thermodynamics. Only interband scatter-
ing washes out the anisotropy between bands,and so
reduces T
c
. Functional derivatives of T
c
with respect
to all four ˛
2
ij
F(§) have beencomputed in[342];these
give some insight into how phonons coupled to the
various bands influence T
c
.
As argued by Nicol and Carbotte [341], there is
compelling evidence for two-band,electron-phonon-
driven superconductivityinMgB
2
.However,the field
has developed along different lines than that re-
viewed so far here for older, more conventional su-
perconductors. It has been argued [343] that it may
well never be possible to extract from tunneling
data detailed information concerning the four spec-
tral functions, ˛
2
ij
F(§), i, j =1, 2. For example, to
date tunneling inversion has not been possible [344].
On the other hand these functions have been cal-
culated from first principles band structure calcula-
tions extended to include the electron-phonon inter-
action. Many of these properties have now been ac-
cepted as fact, though they are based on calculation
only[345–352].Considerablework hasalso beenper-
formed on the determination of the Coulomb pseu-
dopotential parameters [342,353,354]. This param-
eter is most important for the determination of the
value of T
c
,but less important for determining other
superconducting properties. Choi et al. [346, 347]
found good agreement with the temperature depen-
dence of the specific heat by solving the multi-band
anisotropic Eliashberg equations. They found two
distinct sets of order parameters (as a function of
momentum) with some significant variation within
each group.
A more common approach has been to simplify
the problem to one which uses two“isotropic”bands.
For example, a set of ˛
2
ij
F(§), i, j =1, 2 [348–350],
also used by Mitrovi´c [342] and Nicol and Car-
botte [341] along with the corresponding
∗
ij
lead
to good agreement with the specific heat data. Re-
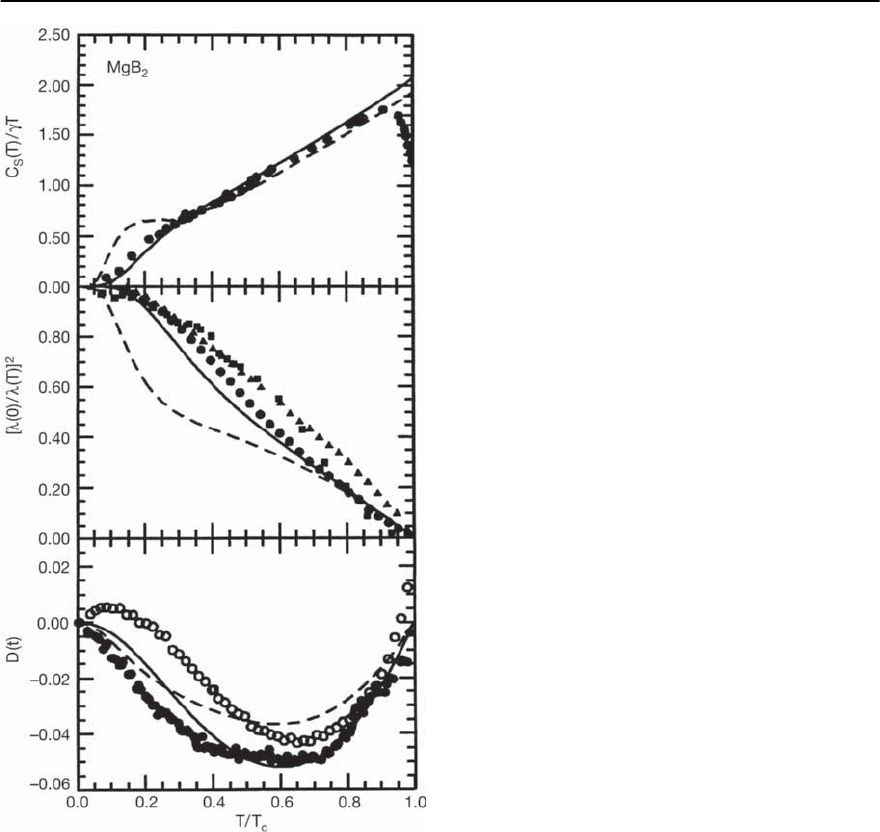
sults are shown in the upper frame of Fig. 3.60. The
solid continuous curve is the result of a full two
band Eliashberg calculation while the solid points
are the data given in [355]. Note in particular the
shoulder near the reduced temperature t ≈ 0.3. This
comes from the second () band. The dashed curve
was obtained by using the same parameters except
that the off-diagonal electron-phonon spectral func-
tion, ˛
2
12
F(§), was arbitrarily halved. The deviation
from experiment at low temperatures is quite sig-
nificant. This illustrates that the agreement achieved
with parameters obtained from first principles cal-
culations is robust. Also note that the calculation
gives a value for the normalized specific heat jump
of 1.08, significantly less than weak coupling BCS,
and in general agreement with experiment, where
values lie in a range 0.82–1.32 [355–358] (see [341]
for further details). Moreover, MgB
2
is an interme-
diate coupling superconductor, with T
c
/!
ln
≈ 0.05,
so that C(T
c
)/ T
c
would normally exceed 1.43 by
about 30% [341].Aswe have seen,anisotropy reduces
144 F. Marsiglio and J.P. Carbotte
Fig. 3.60. Electronic specific heat (upper f rame), penetra-
tiondepth(middle frame),and the deviation function (bot-
tom frame), for MgB
2
. See text for an explanation of the
symbols and curves. From [341]
this value; within the separable model discussed ear-
lier,one would require b ≈ 0.3,whichis anomalously
large.
Nicol and Carbotte [341] find that both the
anomaly at t ≈ 0.3 and the low specific heat jump
can be achieved as follows. Start with two decoupled
bands, i.e. ˛
2
ij
F(§)and
∗
ij
are both zero for i = j.
In this case there would be two critical temperatures,
T
c
and T
c
forthe and band, respectively.More-
over there would be two Sommerfeld constants,
and
.AtT = T
c
(the two dimensional −band
has the higher T
c
) then only the −band contributes
to the jump C(T
c
), but both bands contributeto the
normal state =
+
.If the ’s are roughly the
same size, the normalized jump would be reduced
from a single band case by a factorof 2.Of course the
off-diagonal interaction terms are not zero, so these
remarks would be modified quantitatively. In MgB
2
,
however, the main change from the single band pic-
ture occurs at temperatures near the lower T
c
.Nicol
and Carbotte [341] found that very small values of
and
are required (compared to the diagonal
components
and
)toexplaintheshoulderin
the data at low temperatures.
Additional comparisons with experimental data
are presented in the other frames of Fig. 3.60 [341].
These are the normalized London penetration depth
([
L
(0)/
L
(T)]
2
)andthe deviationfunctionD(t)(see
Eq. (3.140)) vs. reduced temperature t = T/T
c
.The
solid and dashed curves are for the proper Eliashberg
calculation and for that with half the off-diagonal
coupling, as was done for the specific heat.This illus-
trates once again that parameters cannot be changed
very readily; otherwise the agreement with exper-
iment quickly deteriorates. The penetration depth
(deviation function) data is from [348] ( [355,356]),
respectively. Agreement with theory is good, except
for the one set of penetration depth data (solid tri-
angles). However, impurity scattering has not been
included in the calculations (solid curve); this re-
mains as an adjustable parameter which will affect
the relative contribution of each band to the super-
fluid density. Recall that impurity scattering reduces
the superfluid density of a given band,so in the limit
of decoupled bands,each can be tuned independently
by intraband scattering.
In Fig. 3.61 the temperature dependence of the
two gap ratios 2
1
/k
B
T
c
and 2
2
/k
B
T
c
(1 ≡ and
2 ≡ ) are shown [341].The solid curves are the re-
sults of full Eliashberg calculations of the two-band
gap equations, while in the dashed curves the off-
diagonal elements have been (arbitrarily) reduced by
a factor of2.Ascan be seen this change has significant
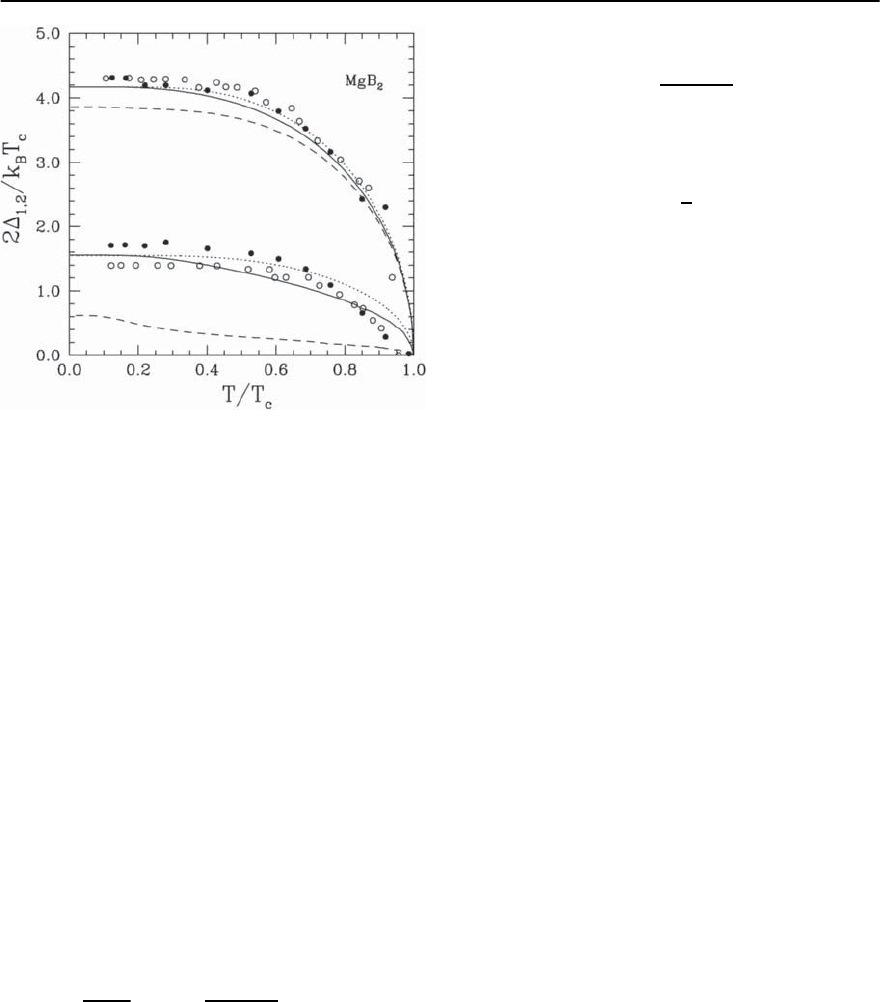
3 Electron–Phonon Superconductivity 145
Fig. 3.61. Gap ratios for the larger (1) and smaller (2) gap
as a function of temperature in MgB
2
. See text for explana-
tions.From [341]
consequences: the gap has been severely lowered
and even its temperature variation is no longer BCS-
like (shown by thedottedcurves).In the extreme case
of no off-diagonalcoupling the dashed curve for the
smaller gap would simply terminate at its own tran-
sition temperature T
c
(much lower than T
c
). Some
of this tendency is seen even in the solid curve, and
is also seen in the data. Any off-diagonal coupling of
course leads to one transition temperature. The data
are from [359] (open circles) and from [360] (solid
circles).
The decoupled bands limit is useful for attain-
ing a first understanding of how the two bands
will qualitatively affect dimensionless BCS ratios. As
we have already mentioned, the normalized specific
heat jump, C(T
c
)/ T
c
=1.43N
∗
1
/(N
∗
1
+ N
∗
2
), where
N
∗
i
= N
i
()(1+
ii
+
i
¯
i
).Here N
i
()isthebareEDOS
at the bare chemical potential in the i’th band, and
¯
i
denotes the complementary band. In the same way
T
2
c
H
2
c
(0)
=0.168
1+˛
∗
1+˛
∗
u
2
, (3.197)
where ˛
∗
= N
∗
2
/N
∗
1
and u ≡
2
(0)/
1
(0) is the ratio
of the two gaps at zero temperature; this value can be
taken as a convenient measure of the gap anisotropy.
A couple of other dimensionless ratios are the re-
duced critical field, h
c
(0) = H
c
(0)/(T
c
|H
c
(T
c
)|), for
which we find
h
c
(0) = 0.576
√
1+˛
∗
u
2
, (3.198)
and, with Y
L
(T) ≡ 1/
2
L
(T), the London penetration
depth ratio,
Y
L
(0)/(T
c
|Y
L
(T
c
)|)=
1
2
(1 + ˛ˇ) , (3.199)
where ˇ ≡ (v
2
F2
/v
2
F1
)(1 +
11
+
12
)/(1 +
22
+
21
)
istheratioofthesquareofthetwoFermivelocities,
suitably renormalized by mass enhancement factors.
Note that here only ˛ is required, not ˛
∗
.Thefactor
˛ is the ratio of the bare EDOs’s at the bare chemical
potential, just as for ˛
∗
,butwithouttherenormal-
izations due to the electron-phonon coupling. These
examples indicate that large changes can occur in
these dimensionless ratios because of the presence
of two bands. If the factors ˛
∗
and ˇ in Eq. (3.199)
are both unity then that ratio is doubled. This is ex-
pected since at T
c
only the −band determines the
slope (in the denominator) while at zero tempera-
ture both bands contribute to the superfluid density;
for the parameters used here,both bands make equal
contributions, resulting in a factor of 2.
To make a connection with the separable
anisotropy model of the older literature, we note
that the two band model reduces to the separable
model through the correspondence
11
= [1+a]
2
/2,
22
= [1 − a]
2
/2and
12
=
21
= [1 − a
2
]andthe
v
f
and N() the same. Note that this model has only
two values for a
k
and thus corresponds to using two
delta-functions for the a
k
in Eq. (3.185), and then
assumes that a
2
small.
3.8 Summary
We have examined a variety of ways in which the
retarded electron phonon interaction influences the
properties of a conventional superconductor. The
first and simplest effect is through a renormalization
of Fermi Liquid parameters, like the effective mass.
While this effect appears in a number of normal state
properties (for example, the low temperature elec-
tronic specific heat capacity, where the Sommerfeld
is enhanced by 1 + — see Eq. (3.137)), it also ap-
pears in many superconductingproperties. The most

146 F. Marsiglio and J.P. Carbotte
obvious (but least measurable) example is in the T
c
equation,Eq.(3.109),where1+ appears in the expo-
nent.Another (perhaps more detectable) occurrence
is in the slope of the upper critical magnetic field. In
each of these cases,the renormalization occurs in the
normal state — its occurrence in the superconduct-
ing state is because the property in question depends
on the normal state effective mass, or Fermi velocity,
etc.One should also bare in mind that the factor 1+,
comes from a weak coupling approach. In a strong
coupling approach, an electron–phonon renormal-
ization is still present,but may be much more signif-
icant than suggested by the weak coupling approach,
and polaron-like physics may dominate [96].
The most important manifestation of the elec-
tron–phonon interaction is the superconducting
state itself. In fact, according to our present under-
standing of Cooper pairing, the electron–phonon-
induced attraction between two electrons would not
overcome their direct Coulomb repulsion, except for
the fact that the former is retarded whereas the latter
is not. This gives rise to the pseudopotential effect;
in some sense the pseudopotential effect is the true
mechanism of superconductivity, rather than the
electron phonon interaction per se. This is perhaps
emphasized in the cuprate materials, where presum-
ably the electrons could not utilize the difference in
energy (and hence time) scales between the attractive
mechanism (whatever it is) and the direct Coulomb
repulsion to overcome the latter. Instead the pair-
ing has apparently adopted a different symmetry (d-
wave) to avoid the direct Coulomb repulsion.
Nonetheless a minimal accounting for these re-
tardation effects accounts fairly well for the super-
conducting ground state. This was accomplished by
BCS theory.A more accurate theory with retardation
effects (Eliashberg theory) quite clearly accounts for
quantitative discrepancies with experiment.Here,Pb
and Hg are held up as paradigms for retardation ef-
fects, the simplest occurring in a measurement of
the gap ratio, for example. The BCS theory predicts
a universal number for this ratio, 2/k
B
T
c
=3.53.
With Eliashberg theory a value for Pb is found close
to 4.5, in excellent agreement with experiment. We
have characterized the discrepancy with BCS the-
ory through a retardation parameter,T
c
/!
ln
.Various
properties have been quantitatively accounted for
through simple analytical expressions with this pa-
rameter, as given in Sections 4.4.4 and 4.4.5 (see [10]
and references therein for many more).
Finally, various dynamical properties exhibit ‘sig-
natures’ of the electron–phonon pairing. These tend
to manifest themselves as ‘wiggles’ in the data, the
most famous of which occurs in the tunneling data,
and allows an inversion to extract the electron
phonon spectral function, ˛
2
F( ). As we saw briefly
in Sect. 4.4.3, andthen again in Sect. 4.4.6, these‘wig-
gles’ occur in various two-electron response func-
tions,most prominentof which is the optical conduc-
tivity. An accurate measurement of these response
functions allows one to infer a significant electron–
phonon coupling.
We have focussed on very conventional supercon-
ductors, and have, for example, avoided any analysis
of the high temperature superconductors. Signs of
electron–phonon interactions have occurred in these
new materials as well, but the relation to the super-
conductivity in them is yet unclear. Moreover, such
effects will no doubt be covered in other chapters.
Nonetheless, we wish to add a few remarks about
other classes of superconducting materials that have
been discovered over the last twenty years.
Cubic Perovskites, beginning with strontium ti-
tanate (SrTiO
3
) [59,60], have already been discussed
in Sect. 4.4.2. As mentioned there, these compounds
(including BaPb
0.75
Bi
0.25
O
3
(T
c
≈ 12 K) [61] and
Ba
1−x
K
x
BiO
3
(T
c
≈ 30 K) [63]) are generally re-
garded as in a distinct class from the high-T
c
cuprates. This has left them, somewhat by default,
as electron–phonon driven superconductors.On the
other hand,there is strong optical evidence [189,316]
that the electron–phonon interaction is very weak in
these materials. Hence, as far as we are concerned,
the mechanism of superconductivity in these per-
ovskites is not understood at all. Tunneling stud-
ies [319,320] are divided on this issue.
One- and two-dimensional organic superconduc-
tors were discovered in 1979 [361]. The subject had
developed sufficiently so that, by 1990, a book de-
voted to the topic was written [362]. Organic super-
conductivity represents another interesting idea that
was first presented by theorists [110,111], on the ba-
