Беграмбеков Л.Б. Процессы в твердом теле под действием ионного и плазменного облучения

Подождите немного. Документ загружается.

131

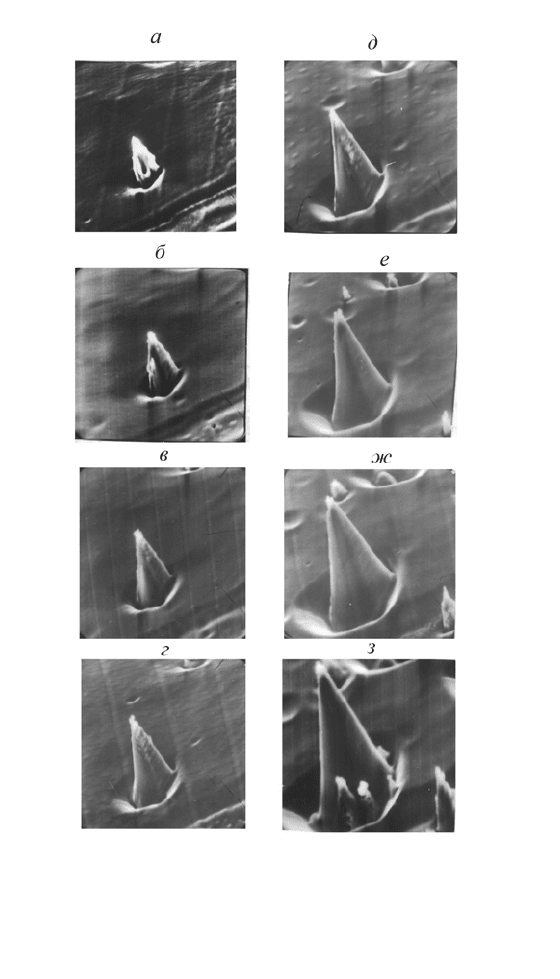
Рис. 5.11. Развитие конуса в период стабилизации [7].

Медь, ионы Ar

Е=600 эВ, j=3х10

см

-2

. Время облучения

(мин): а — 90, б — 110, в — 130, г — 150, д — 170, е —

200, ж — 230, з — 250 с.

132

Модель, объясняющая существование периода стабильной формы и

других закономерностей развития конусов, основывается на пред-

ставлении о том, что ионная бомбардировка не только создает, бла-

годаря распылению, конические формы, но и способствует развитию

сжимающих напряжений на их поверхностях при определенных уг-

лах наклона (θ

) склонов конусов (рис. 5.12) [56, 58]. Вершина кону-

са размером R≈L, где L — глубина напряженной приповерхностной

зоны, остается свободной от напряжений. Поэтому по склонам кону-

са в вершину устанавливается диффузионный поток, компенсирую-

щий ее распыление. Таким образом, развитие конуса есть результат

того, что благодаря ионно-стимулированным процессам на поверх-

ности склонов и в приповерхностных слоях, распыление его верши-

ны происходит медленнее, чем распыление окружающей плоской

поверхности. В результате, высота конуса увеличивается в процессе

развития, хотя его вершина всегда ниже уровня первоначальной по-

верхности.

Рис. 5.12. Схема развития конуса [56]: а — первоначальный выступ,

б — шарик на ножке, в-г — период стабилизации формы конуса и

скорости его роста, д — разрушение вершины и увеличение угла

наклона склонов, е — распыление и исчезновение конуса.

133

Напряжения по склонам конусов возникают при выполнении

условия θ

> π - 2ϕ

кр

. За величину ϕ

кр

принимается угол падения ио-

нов, при котором атомы поверхности склона при столкновении с

налетающим ионом получат энергию Е

, достаточную для образова-

ния междоузельного атома в глубине мишени по механизму заме-

щающих столкновений:

кр

cos φ

()

, (5.11)

где М

и М

— массы иона и атома поверхности соответственно. В

большинстве случаев вместо Е

можно использовать энергию сме-

щения Е

. Оценка представляется оправданной для ионов средних и

тяжелых масс с энергиями Е

≤ 1 кэВ, когда можно пренебречь их

внедрением в поверхность при наклонном падении.

Если ϕ

кр

<ϕ

mаx

, то диффузионный поток заостряет вершину, но

не приводит к изменению угла между склонами и скорости распыле-

ния конуса в целом. Если же ϕ

кр

>ϕ

mаx

, то в этом случае диффузион-

ный поток в вершину в совокупности с распылением приводит к ус-

тановлению такого угла θ

между склонами, что скорости разруше-

ния склонов и вершины сравниваются (

hh= ). В предположении

конической формы вершины конуса условие равновесия

[]

cos φ

(θ ) (θ )

sin φ

it s

jS S

kTL

=−

. (5.12)

Здесь θ

— угол при вершине конуса и θ

— угол между на-

правлением ионного пучка и нормалью к поверхности.

Эта конфигурация оказывается относительно стабильной. При

увеличении по какой-либо причине скорости разрушения вершины

(увеличение коэффициента распыления, уменьшение диффузионно-

го потока) уменьшается наклон склонов конуса в верхней его части,

и, в результате, усиливается диффузионный поток в вершину. Про-

цесс развивается до тех пор, пока скорость разрушения склонов и

вершины вновь не сравниваются уже при несколько большем значе-

нии угла θ

. При замедлении разрушения вершины картина будет

134

обратной. Если условие (5.12) выполняется при углах ϕ

>ϕ

mаx

, та-

ких,что S(ϕ)<S(0), то высота конуса будет увеличиваться со скоро-

стью:

[]

(0) (φ )

hjaS S=−. (5.13)

Подобным же образом напряжения на облучаемых склонах

влияют на развитие кольцевой канавки конического сечения вокруг

конуса. Под их влиянием формируется поток вакансий в область

дна углубления, где уровень напряжений оказывается повышен-

ным. В результате предотвращается образование плоского дна, ста-

билизируется его форма и скорость роста глубины. Часть материа-

ла из углубления благодаря диффузии поступает на склоны конуса.

Материал поступает на склоны конуса также благодаря перенапы-

лению со склонов канавки и с окружающих его участков плоской

поверхности.

Используя формулу (5.13) и зависимость S(ϕ), можно оце-

нить возможность роста конусов при данных энергии и типе ионов,

виде мишени. При Е ≤ 1 кэВ величина [S(0)-S(ϕ

кр

)] > 0 для пар

→Cu, Ar

→Au, Hg

→Ta. Это условие не выполняется,

т.е. конусы не будут расти в случае Ne

→Mo, Ar

→Ta, Ar

→W.

Конусы могут образовываться в тени затеняющего элемента, на-

пример вискера (рис. 5.13), но не будут расти после его распыле-

ния.

Последовательный учет роли напряжений и формируемых

ими диффузионных потоков по склонам конусов позволяет объяс-

нить не только причины роста конусов, но и специфические осо-

бенности конусообразования, отмечаемые в различных экспери-

ментальных условиях [58].

Изменение формы вершины конусов — округление, заостре-

ние, образование наплывов, иногда напоминавших своеобразные

покрытия, образование "шариков", смещение вершины, появление

нескольких микровершин — определялось колебаниями скорости

распыления, величины диффузионного потока по склонам или на-

рушением его симметрии. В результате действия механизма стаби-

лизации эти изменения формы вершины не оказывали влияния на

рост и форму конусов в целом.

135

Если в результате флуктуации перечисленных выше пара-

метров или, благодаря внешнему воздействию вершина "затупля-

лась" таким образом, что ее диаметр существенно превышал тол-

щину напряженного слоя, то диффузионный поток по склонам уже

не мог восстанавливать вершину. В результате формировался свое-

образный кольцевой гребень по периферии вершинной области или

вырастала новая вершина вдоль одного из склонов, если ионная

бомбардировка происходила не по нормали к плоской поверхности.

При развитии конусов у поверхностных ступенек, на краю

образцов или при близком расположении конусов потоки перена-

пыляющихся атомов и отраженных ионов на стороны конусов ока-

зывались несимметричными. Это вызывало асимметрию напряже-

ний и диффузии на сторонах конусов и их изгиб. Возрастающая

плотность ионного облучения изогнутой части конуса интенсифи-

цировала диффузионные потоки, и в результате она удлинялась и

утончалась (рис. 5.14).

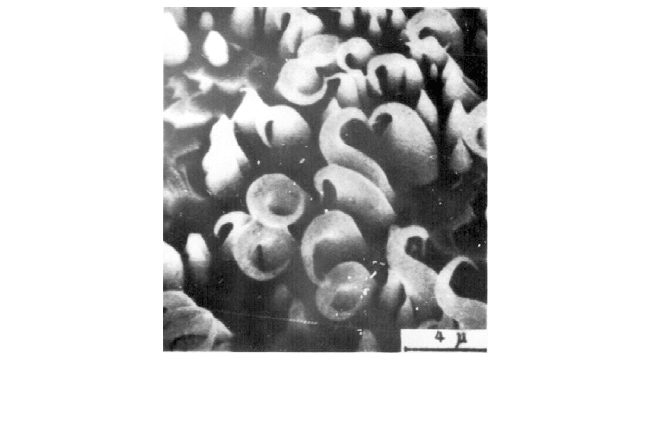
Рис. 5.13. Формирование конусов в "тени" вискеров и

выступов [7]. (Медь, Hg

, 200 эВ.) Увеличение — 6000

136

Если поток тугоплавкой примеси на поверхность прекращал-

ся, то уровень напряжений на склонах и, соответственно, диффузи-

онный поток в вершину со временем уменьшались. При этом рав-

новесный угол θ

увеличивался, начиная с вершинной области, и

постепенно распространялся на весь конус. Рост конуса замедлял-

ся, а затем после достижения условия S(ϕ

)>S(0) начиналось его

распыление. Глубина окружающего конус углубления также пере-

ставала увеличиваться, у него появлялось и росло плоское дно ме-

жду отступающими во время распыления склонами (рис. 5.15).

При появлении на поверхности структуры, состоящей из

тесно расположенных конусов, их развитие определяется некото-

рыми дополнительными аспектами. В частности, значительная

часть атомов, распыленных со склонов, осаждается на соседние

конусы, способствуя замедлению распыления всей структуры ко-

нусов. Кроме того, при интенсивном перенапылении увеличивают-

ся напряжения на склонах конусов и, соответственно, интенсифи-

цируются процессы роста. В результате, при тесном расположении

равновесный угол при вершине оказывается меньшим, чем у оди-

ночных конусов. Следует также отметить, что бомбардировка рас-

Рис. 5.14. Изогнутые конусы [57]. (Mедь, Ar

КэВ.) Увеличение — 4500

137

пыленными со склонов атомами соседних участков поверхности

способствует росту напряжений и появлению там новых конусов.

Это, предположительно, является одной из причин самовосстанов-

ления структуры тесно расположенных конусов.

На определенных кристаллических гранях и при не слишком

высоких температурах и потоках облучения конусы приобретали

пирамидальную огранку. Условия такого развития выявлены не-

достаточно.

Процессы, связанные с ионно-стимулированными напряже-

ниями, и перенапыление играли основную роль в образовании ко-

нусов и пирамид на выступах и гребнях или в углублениях, ямках

травления и т.п. В первом случае выпуклая форма рельефа способ-

ствовала формированию диффузионных потоков в их вершины, во

втором — бомбардировка дна углублений атомными частицами,

рассеянными и распыленными с их склонов, инициировала рост

напряжений и формирование первоначальных выступов. Второй из

указанных процессов является основной причиной появления ко-

нусов в поверхностных порах (раздел 5.3.3).

5.3.3. ПОВЕРХНОСТНОЕ ПОРООБРАЗОВАНИЕ

В этом разделе рассматриваются условия появления и зако-

номерности развития микроскопических пор (углублений) на по-

Рис. 5.15. Конус на стадии разрушения [7].

(Медь, ионы Hg

, 50 эВ.) Увеличение —1500

138

верхности твердого тела, облучаемого ионами плазмы [59]. Поры

появлялись на поверхности твердых тел при их бомбардировке ио-

нами легких газов в условиях высоких температур. На поверхности

плотного мелкозернистого графита МГТ-8 при облучении ионами

гелия He

(E = 800 эВ, j = 1.2 мА/см

) поверхностные поры наблю-

дались в диапазоне температур от 500 и до 1300 °С, предельной

температуры экспериментов. Они появлялись при дозах примерно

0.4×10

ион/см

. Средние размеры пор составляли около 5 мкм и

были сравнимы с толщиной распыленного слоя. В диапазоне доз

(0.4÷2.2)× 10

ион/см

концентрация пор увеличивалась в 5÷7 раз и

достигала величины 3×10

см

-2

(рис. 5.16). Количество пор росло

экспоненциально с дозой облучения (рис. 5.17).

При облучении медно-никелевого сплава Cu-Ni 50 ат % ио-

нами гелия (E = 600 эВ, j = 1 мА/см

) при температуре 550 °С появ-

ление пор было зарегистрировано при дозах облучения

(0,5÷1)×10

ион/см

Поры уже в первый момент их регистрации

после начала облучения имели значительные размеры (рис. 5.18).

Концентрация пор оказывалась выше вдоль границ поверхностных

кристаллитов, царапин и т.п. Видно, что, сливаясь друг с другом,

тесно расположенные поры образуют каналы по границам поверх-

ностных кристаллитов (рис. 5.19, а). Поры примерно тех же попе-

речных размеров, хотя и в меньшем количестве, появлялись и на

прилегающих к облучаемой области, но не облученных участках

поверхности (рис. 5.19, б). Следует отметить, что образование пор

фиксировалось на поверхности нагреваемых металлов также и в

отсутствии ионного облучения.

139

Рис. 5.16. Поры на поверхности графита МПГ-8 [59].

(He

, 800 эВ.) Увеличение — 1000

012

Количество пор

Доза облучения

см

-2

см

-2

Рис. 5.17. Зависимость концентрации пор на поверхности графита

МПГ-8 от дозы облучения ионами He

с энергией 800 эВ [59]

140

а б

Рис. 5.19. Поры на поверхности сплава Cu-Ni50 ат %: а — на поверхности,

облученной ионами гелия [59] (Е=600 эВ, j = 1 мА/см

, Φ=3,2×10

ион/см

Т=550

С), б — прилегающих к облучаемой области, но не облученных уча-

стках поверхности. Увеличение — 1000

0123456

Доза облучения

Средний диаметр пор

мкм

см

-2

Рис. 5.18. Зависимость поперечного размера пор на поверх-

ности сплава Cu-Ni 50 ат % от дозы облучения ионами He

энергией 600 эВ [59]