Bear H.S. Understanding Calculus
Подождите немного. Документ загружается.


28
Understanding
Calculus
Solution
The volume of a cone is
~rrr2h,
and since here r = h, V =
~rrh3.
We are given that
~~
= 5, and the
chain rule shows that
dV
2dh
-
=rrh
-
dt dt
Therefore, 5 =
rrh2~,
and
~
= 5/rrh
2.
When h = 4,
~
= 5/16rr ft/min.
EXAMPLE
5.2
A car drives east at 40 mph starting at town A, which is 60 miles due south of town B. At what rate is
the distance (as the crow flies) between the car and town
B increasing when t = 2 hr?
Solution
If s is the distance between the car and town B, and x is the distance from the car to town A, then
S2 = 60
2
+ x
2
.
Hence,
ds dx
2s-
=
2x-.
dt dt
When t = 2, x = 80 and
s =
)60
2
+ 80
2
=
)10,000
= 100.
Since
~
= 40,
ds x 80
- = - .40 = - .40 = 32(mi/hr).
dt s 100
PROBLEMS
Find
~.
dx
5.1 y = (1 + 3X)4
5.2 y = (x + x
2
) 5
5.3 y = (1 + 2X)-1
5.4 y = (x
3
+ X
7)-1O
1
5.5
y=--
2+3x
1
5.6 y = 1
+x
2
5.7 y =
v"f+X2
5.8 y =
(-IX
+ 1)3
(
2X
+
1)3
5.9 y = 1+ x
2
(
JX
)5
5.10 y =
--
x+l
1
5.11
y=
~
x
3
- 2
5.12 y =
(J"l+X
+X)-2
Write *in terms of x:
5.13 z =
y-3,
Y = 2x + 1
5 1
5.14 z =
y,
y =
--
x+l

Chapter 5 • The Chain Rule
29
1
5.15 Z = -, y =
v'X
y
1
5.16 Z =,JY, y = -
x
1
5.17 Z =
-,
w
=,jY,
y = x
2
+9
w
5.18 Z = w
2
, W = 1
+,jY,
y = x + 1
5.19 If a rectangle has sides x and y and x is increasing at 1 ern/secand y at 3 ern/sec, how fast
is the area increasing when
x =4 and y =5? Hint:
dA d dy dx
dt
= dt (xy) =x dt + y dt .
5.20 In Example 5.1 suppose the grain flows out of the spout at 3 cu ftlmin and the pile retains
the shape of a cone with height equal to the diameter of the base. At what rate is the height
increasing when
h = 6? At what rate is the area of the base of the cone increasing when
h = 6?
5.21 The temperature on a rod is given by
T = 3 +
v'X
where x is the distance from the left end
in inches and
T is measured in degrees Centigrade. A sensor moves along the rod so that
its position after
t seconds is x = t +
~
t
3.
At what rate is the temperature at the sensor
changing when
t = 2?
5.22 Water flows into a cylindrical bucket at 10 cu in/sec. The bucket has diameter 1
f1.
How
fast is the water rising in the bucket?
Hint: The volume V of water in the bucket is Jr6
2
y
irr', where y is the height of the water in inches.
5.23 A spherical balloon is inflated so that its volume at time
t
is,JI+t.
At what rate is the
radius
r increasing when r = 5?
(V
=
~Jrr3)
5.24 Two ships leave the same dock at the same time. One goes east at 20 knots and the other
north at 10 knots. At what rate (nautical miles per hour) is the distance between them
changing when
t = 3 hr? (1 knot is one nautical mile (1.15 miles) per hour.)
5.25 The top half of the circle
x
2
+
y2
= a
2
has the equation y = Ja
2
-
x
2
•
Find the slope of
the tangent at
(x,
Ja
2
-
x
2
) ,
and show that the tangent is perpendicular to the radius to the
point; that is, show that the tangent has slope
-x
/ y .
5.26 An object moves along the x-axis so that its position at time t is given by x = (t
2
-
4t)3.
The object moves to the right when
~
> 0 and to the left when
~
<
O.
When does the
object change direction?
5.27 Suppose
f'ex)
=
~.
If
g(x)
=
f(x
2
+
x),
what is g'(X)?

Trigonometric Functions
In trigonometrycourses, the functions sinx and cosx have to do with the angle x. If x is an
acute angle in a right triangle (Figure 6.1), then sinx is the opposite side over the hypotenuse
and cos
x is the adjacent side over the hypotenuse. If the hypotenuse has length 1, then the
opposite side has length sin
x and the adjacent side has length cos x.
In calculus we more often think of sinx and cosx as functions of a number x. Suppose
you start at the point (1, 0) and go x units around the unit circle in the counterclockwise
direction. The point you arriveat has coordinates(cos
x, sin
x)
as indicated in Figure 6.2. For
calculus purposes this is the definitionof cos
x and sinx. The angle at the origin which cuts
off an arc of length
x on the unit circle is an angle of x radians. If x is a negative number,
then cosx and sin x are the coordinatesof the point which is IxIunits around the circle in the
clockwise direction. The picture showsthat for all x,
cos(
-x)
= cosx; sin(
-x)
= - sinx.
Since the unit circle has length 2n , the angle
2n"
radianscorrespondsto 360°. From this
wecan easily calculatethe equivalentradian measurefor any numberof degrees. For example,
30° correspondsto
:~o
. 2rr = %radians, and 90° correspondsto
3~
• 2rr = I radians. Table
6.1 givesthe values of cos
x and sinx for common values of x correspondingto angles in the
firstquadrant.
For angles outside the firstquadrant (radian measureoutside [0,
I
]),
we read the values
of cos
x and sin x from the appropriatediagram as indicatedin Figure 6.3. From the definition
it is clear that if you go Zn units around the circle from the point x units from (1, 0) you get
back to the same point (cos
x, sin
x).
That is, for any x,
sin(x +
21l')
= sinx,
cos(x +
21l')
= cosx.
The functions cos
x and sinx are thus periodic functions with period
21l'
.
The remaining four trigonometric functions are definedas follows:
sinx
tanx =
--;
cosx
cosx
cot x
=
-.-;
smx
1 1
sec x =
--;
cscx
=
-.-.
cosx smx
We will deal almost entirely with cosx, sinx, tan x, and secx.
31
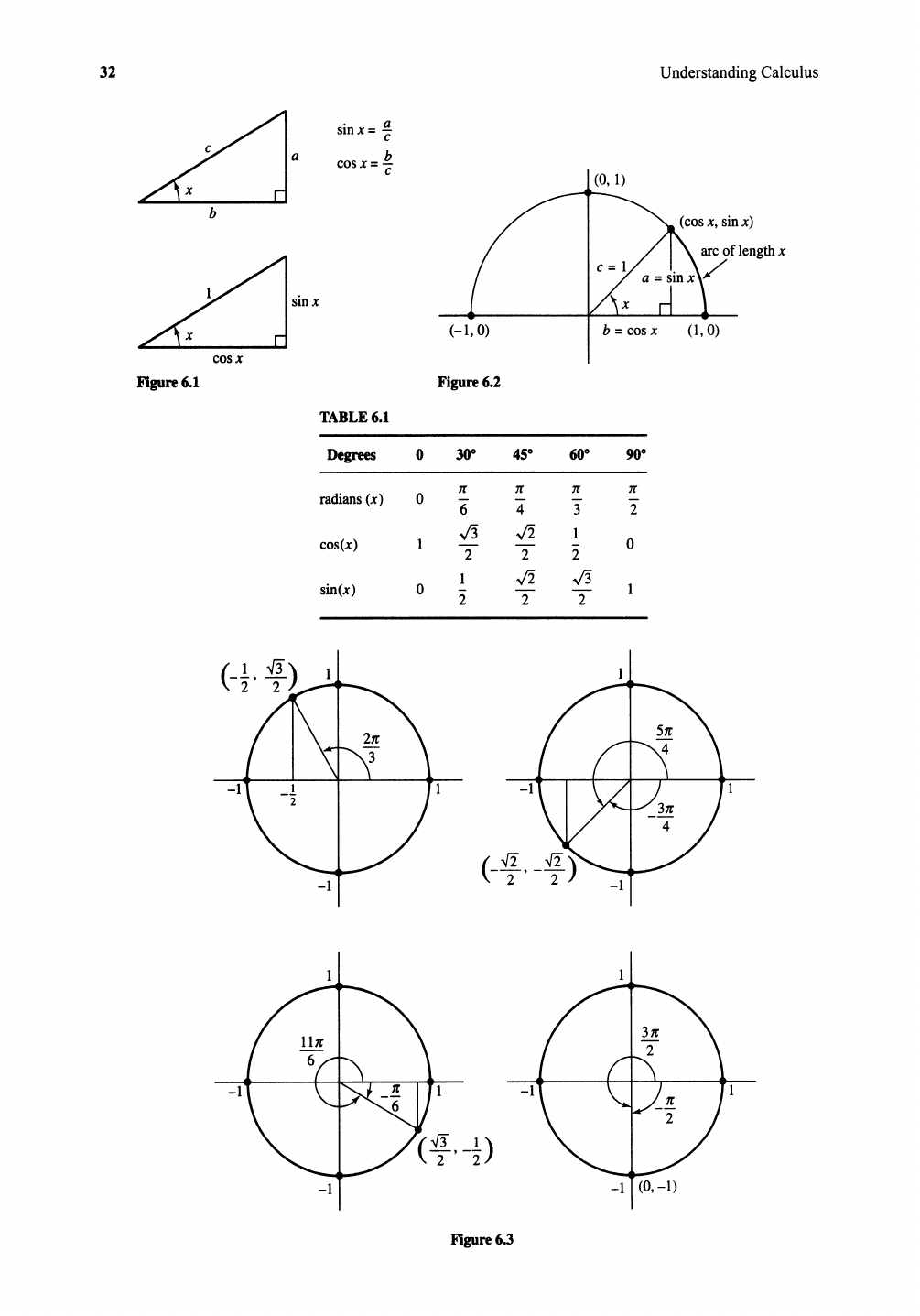
32
a
. a
sm x =C
cosx =
lz..
c
Understanding Calculus
(0, 1)
b
sinx
(-1,0)
b = cos x
(1,0)
cosx
Figure 6.1
Figure 6.2
TABLE6.1
Degrees
0
J00
45°
60°
90°
radians
(x)
0
n x
1r 1r
6
4
3
2
v'3
v'2
1
0
cos(x)
2
2
2
0
1
v'2
v'3
sin(x)
2 2
2
-1
-1
-1
Figure 6.3
-1
-1
(0,-1)

Chapter6 • Trigonometric Functions 33
(6.2)
The following identities are used constantly in our calculations and should be memorized.
(i) sin
2
x +cos
2
X
= 1
(ii) sin(x
+y) =
sinx
cos y +
cosx
sin y
sin(x - y) = sinx cos y - cosx sin y
(iii) sin 2x =2 sin x cos x
(iv) cos(x
+ y) = cos x cos y - sin x sin y
cos(x - y) = cosx cos y +
sinx
sin y
(v) cos 2x = cos
2
X - sin
2
x
= 1 - 2 sin
2
x
=
2cos
2
x-I
(vi) cos? x = 4(1 + cos
2x)
(vii) sin
2
x = 4(1 - cos 2x)
(viii) tan
2
x + 1 = sec
2
x.
The first identity, (i), simply says that (cos
x, sin
x)
is a point on the unit circle. Identities (ii)
and (iv) are not too hard to verify, but the verification does nothing to uplift the spirit and so
will be omitted. Identities (iii) and (v) for sin 2x and cos
2x,
respectively, follow from (ii)
and (iv) by substituting x for
y. The alternative forms for cos 2x in (v) result from replacing
cos
2
x by 1 - sin
2
x or sin
2
x
by
1 - cos
2
x. These last two equations give the formulas (vi)
and (vii) for cos
2
x and sin
2
x in terms of cos
2x,
and these will be used later to integrate
cos? x and sin
2
x. The final identity involving tan? x and sec? x results by dividing the identity
sin
2
x +cos
2
X = 1 through by cos
2
x.
To differentiate the trigonometric functions, we will need the following limits:
lim sinx = 1, (6.1)
x~o
x
1
· 1 -
cosx
0
Hfl = .
x~o
x
The geometry of Figure 6.4 suggests that
. sin x
sm r
< x <
--,
cosx
and these inequalities do indeed hold for all x with 0 < x < I. From the first inequality we
get
sinx
--
< 1,
x
and from the second we get
sin
x
cosx
<
--.
x
(0, 1)
Figure 6.4
(-1,0)
Arc lengthx
tan x = sinx
~
cos x
\
(1 - cos x)

34
Understanding
Calculus
Putting these together we have
sinx
cosx
<
--
< 1. (6.3)
x
Since cos x
~
1 as x
~
0, sin
x]
x
~
1. To see what happens as x
--+
0 through
negative values, notice that cos(
-x)
=
cosx
and sin(
-x)/(
-x)
= sin
x]
x,
so (6.3) still holds
for negative
x.
To verify (6.2) we notice from Figure 6.4 that the arc of length x is longer than the
hypotenuse of the right triangle whose sides are sin
x and 1 - cos x. Therefore,
sin
2
x + (1 - cos
xr'
~
x
2
,
sin
2
x + cos
2
X + 1 -
2cosx
~
x
2
,
2 -
2cosx
~
x
2
,
1 -
cosx
1
---<-x.
x - 2
Hence, (1 -
cosxv]»
~
0 as x
~
0, which is (6.2). This limit can also be deduced from
(6.1) by algebraic manipulation as follows:
1 - cos
x (1 - cos
x)
(1 + cos
x)
---
=
--------
x x(1 + cosx)
1 - cos
2
x
sinx
sinx
=-----=
x(1 +cos x) x 1 +
cosx
Since sinx
~
1 and
~
--+
0 as x
~
0 we again get that
l-cosx
~
o.
x (1+cosx) , x
Now we can calculate the derivatives of sin x and cos x.
d.
. sin(x +
~x)
- sin x
-SInx
= lim
dx Lix-.+O
~x
sin x cos
~x
+ cos x sin
~x
- sin x
= lim
Lix-.+O
~x
. . (cos
~x
- 1) sin
~x
= lim Sinx +
cosx--
Lix-.+O
~x
~x
= (sinx)
·0+
(cos
x)
. 1
=
cosx.
We differentiate cos x using the identity
. (
Jr).
n . n
SIn
x·+ - = sIn x cos - + cos x sIn -
222
= (sinx)
·0+
(cosx)
·1
=
cosx.
Therefore,
~
cos x=
~
sin
(x
+
~)
dx dx 2
=cos(x+i)
Jr . . Jr
= cos X cos - -
SIn
x sIn -
2 2
= (cosx)
·0-
(sinx) . 1
= -
sinx.

Chapter6 • Trigonometric Functions
35
d .
- cosx =-
smx
;
dx
The derivatives of tanx and secx are easilycalculated (Problem 6.2), andthe four basic
trigonometric differentiation
formulas
are
d .
-smx
=cosx
;
dx
EXAMPLE 6.1
Find
'!1:.
if
dx
d
- tanx =sec
2
x;
dx
d
- secx =secx tanx .
dx
(i) y =sin(x
3
+ 1);
(ii) y = cos3x +tan?x;
(iii) y =sec
JX
.
Solution
Each of these problems
involves
a chain rule differentiation.
(i)
:~
= :xsin(x
3
+ I) =[cos(x
3
+ 1)]3x
2
;
dy d
(ii) - = - (cos3x + tarr'
x)
=
-3
sin3x + 2 tanx sec?x ;
dx dx
(iii) dy =
~
(sec
JX)
= (sec
JX
tan
JX)
lr.:.
dx dx
2
y
x
EXAMPLE 6.2
A searchlight, rotating at 3 radians/min, plays a spot on a wall that is 100 ft away. At what rate is the
lightedspot traveling along the wallwhen the beam is perpendicular to the wall?
Solution
Measuredistancealongthe wallfrom the point,0, directlyoppositethe light (Figure6.5). Weare given
that
¥r
=3. Sincex/IOO =tan0,
dx
d
- =
-IOOtanO
dt dt
dO
=
IOOsec
2
edt '
Whenx =0, 0 =0,
sec?
0 = 1, then
¥r
=300 ftlmin or 5 ftlsec.
Figure
6.5
PROBLEMS
6.1 Graph y = sinx and y =cosx on the same coordinate systemfor °
::::
x
::::
2:rr
. Use your
calculator(set for radians, not degrees)to findvaluesfor
x = 0, 0.5, 1.0, 1.5, . . .
,5
.5
,6
.0,
6.28.

36
Understanding Calculus
6.2 Derivethe formulas f tan x = sec
2
x and f secx = secx tanx, using -dd sinx = cosX
d •
x x x
and d;
cosx
= - smx.
Find
*.
6.3 y =
cos2x
6.4 y = sin(3x + 1)
6.5 y =
cos?
x
6.6 y =
cosx
sinx
6.7 y = sin
2
8x
6.8 y =cos
3(5x
+ 1)
6.9 y =
Jl
+cosx
6.10 y = (sinx + cosx)?
6.11 y = x secx
6.12 y = tan(4x)
6.13
y = secx tanx
6.14 y = sec
2
x-I
6.15 y = tan?x
6.16 y = sec' x
sinx
6.17
y=
---
I +
cosx
6.18 y =(tanx + 1)2
6.19 y = (2x
2
+ 1) cos3x
6
sin5x
.20
y=--
x
6.21
y = x
2
•
+ 1
sinx
6.22
y = x
sinx
cosx
6.23 Deriveidentities(vi) and (vii) from (v).
6.24 Show that 4sinx =sin
~
cos
~.
6.25 Showthat tan(x + y) = tanx + tan
y
•
l-tanx
tan y
6.26 In the situation of Example 6.2, at what rate is the lighted spot traveling when the beam
makesan angleof 45
0
with the wall?
6.27 A pendulum swings so that the angle
(}
the rod makes with the vertical is given by
(}
=
f2
sin(wt), wherew is a constant and t is measuredin seconds.
(i) If the pendulum is at its maximumswing from the verticalfor the firsttime at
t = 1,
whatis
u),
andwhatis the nexttimethe pendulumis at its maximumswingon the other
side of its arc?
(ii) Let x be the point on the ground directlyunderthe pendulum,withx = 0 when t =
O.
If the pendulumis 30 in long, what is
~
when t = I? When t = 2? t =3?
6.28 Let
(}
be the angle a ladder makes with a wall. If the ladder is
10ft
long and the base is
pulledawayfrom the wall at 3 ft/sec, what is
¥i
whenthe top of the ladderis 5 ft abovethe
floor?
6.29 A boat passes point A goingeast at 44 ft/sec. A searchlightat B, 200 feet south of point A,
followsthe boat. At whatrate is the searchlightturningafter 3 seconds?
Hint:
Let (J be the
angle betweenthe line
AB and the line from B to the boat; find
~.
6.30 Showthat cosx = sin(x +
I).
6.31 Showthatfor any two numbersa and b such that a
2
+b
2
= 1 there is a number()such that
a = cos
(},
b = sin
(}.
How many such numbers
(}
are there?

Chapter6 • Trigonometric Functions
37
6.32 Everycurve y = A sinx +B cosx is a sinecurve;thatis, for all A and B thereare
numbers
K and(j such that A sinx +B cosx = K sin(x +
(j).
Hint:
Write
ASinx+BcosX=JA2+B2[(SinX)
A +(cosx) B
].
JA2+
B2
JA2+ B2
Noticethat if a =
~
and b =
~,
thena
2
+b
2
= 1. ConsultProblem6.31.
v
A2+B2
v
A2+B2
Find all pointsx in [0,
2n]
wherethe tangentline is horizontal.
6.33
y = sinx
6.34 y = cosx
6.35 y = sinx + cosx
6.36 y =sirr'x
6.37
y =x - tanx

Exponential Functions
and
Logarithms
The exponentialfunctions are the functions of the form y = a", where a is a positive constant.
For example,
are exponential functions.
Consider for a moment what
a" means for a positive number a and an arbitrary real
number x. If x is an integer, there is no problem: a
2
,
a
5
,
a
-3
-these
expressions are part of
arithmetic. If
thf
eXfonent x is a fraction,
the~
~x
is no longer just multiplication or division.
For example, a
2,
a 3 are the roots of a, and It
IS
a fact that we here take for granted that a
positive number has a square root, cube root, and so on. If x is a fraction, say x =
~
for
positive integers
p and q, then a
~
is the
pth
power of the
qth
root of a. That takes care of
rational exponents
x. If x is an irrational number like
,J2
or n , then aX is the limit of the
numbers
a
~
where the rational numbers I!. approach x. It is a theorem that the limit exists and
that exponentials defined this way
satisfyq
all the usual rules for all exponents x.
Notice the distinction between the exponential function a" and the power function x" .
In the power functions we have considered so far, y = x
2
,
y = x
4,
y =
x-
3
,
and so on, the
base x is the variable, and the exponent is fixed. In the exponential function a", the exponent
is the variable. The graphs of
y = 2
X
and y =
<!)X
are shown in Figure 7.1. Notice that the
two curves are symmetric about the y-axis, since
<!)X
=
2-
x
•
The curve y = aX for a > 1 will rise steeply as x increases, and decrease rapidly to
zero as
x
~
-00.
If 0 < a < 1, then the curve decreases rapidly to zero as x
~
00,
and
increases sharply as x
~
-00.
39
