Bear H.S. Understanding Calculus

Подождите немного. Документ загружается.

Chapter I • Lines

(*)

1.4 y = 2x - 3

1.5 y =

-x

- 1

1.6 x + 3y =0

1.7 2x + 3y + 6 = 0

Write the equations of the following lines, and put the equation in the slope-intercept form y =

mx+b.

1.8 through (1, 1) and (3, 0)

1.9 through

(-2,3)

and (4, 1)

1.10 with y-intercept 7 and slope 2

1.11 with y-intercept

-1

and slope

-4

1.12 through

(1,4)

with slope

-3

1.13 through (2, 3) and perpendicular to x - 2y + 1 = 0

1.14 through

(1,2)

and parallel to 7x - y =4

1.15 (i) Show that the lines x + y - 3 =0 and x - y + 1 = 0 intersect at

(1,2).

(ii) Show that for any constant k

(x - y + 1) +

k(x

+ y - 3) =0

is the equation of a line through (1, 2).

(iii) Find

k so that the line (*) goes through

(1,2)

and

(2,4),

and write the equation of the

line.

1.16 Find the equation of the line through

(1,1)

and the intersection of the lines x - 2y +2 = 0

and

x + y - 4 = O.

Hint:

See Problem 1.15. Notice that you

don't

have to find the

intersection of the given lines.

1.17 Find the equation of the line with slope 2 which passes through the intersection of the lines

x + 2y - 5 =0 and 3x + y - 7 =O.

1.18 Find the equation of the line through the intersection of x +3y - 2 = 0 and 2x +y - 5 = 0

which is perpendicular to

x + 3y - 2 = O.

1.19 Find the angle (i) between the lines y = 2x and y = 3x; (ii) between the lines y = 2x - 5

and y = 3x + 7.

1.20 Find the line through

(3,4)

which makes an angle of 25° with the x-axis.

Parabolas,

Ellipses,

Hyperbolas

Mathematicians inancientGreecediscovered thatif youcut a cone witha plane,yougetcurves

with very interestingproperties. For example,if the plane is perpendicular to the axis of the

cone, you get a circle. Tilt the planea little and the circlebecomesan ellipse. Keeptiltingand

at one critical angle the curve is a parabola. Anyfurther tilts yield a hyperbola. These curves

are still of basicinterest,and we will encounterthem frequently. In the coordinateplane these

curves, called conic sectionsfor the obviousreason, all haveequationsof the seconddegree.

We will considerthe following simplecases:

y =

+C, parabolas;

x2 y2

+ b

= I, ellipses;

x2 y2

= ±1, hyperbolas.

Consider first the parabola

y = x

•

The graph is symmetric about the y-axis since

(

-x,

y) lies on the curve whenever (x, y) does. The graphis shownin Figure 2.1.

If the coefficient of

is larger (e.g., y = 2x

then the curve heads up more sharply,

and if the coefficient is negative (e.g.,

y = -

the curve headsdownward as

Iincreases.

All the curves y =

+C with A

0 are parabolas, and they all have exactly

the same shape as

y =

•

The axis of the parabolawill moveright or left depending on B,

and the curve will move up or down dependingon

Band

C, but the shaperemains the same

as y

•

Consider, for example, y =x

4x +3. We showthat this curve has the same

shape as y =x

by completingthe square:

y = x

4x + 3,

y =x

4x + 4 - 1,

y = (x - 2)2 -

.1.

The graph of y = (x - 2)2 is just the graph of y = x

movedover so that its axis is the line

x = 2. The constant

-1

drops the whole curve down one unit. The three curves y = x

Y = (x - 2)2, and y = (x - 2)2 - 1 are shownin Figure 2.2.

-3

-2

-1

Figure 2.1

2 3

Figure 2.2

Understanding Calculus

The

distance'

between points (XI, YI) and

(X2,

Y2)

is given by

r = J(X2 - XI)2 +

(Y2

- YI)2.

It follows that the circle with center (xo,

Yo)

and

radius,

is characterized by the equation

J (x - xo) + (y -

YO)2

= r

(x -

xO)2

+ (y -

YO)2

= ,2.

From (2.1) we see that every circle has an equation of the form

+y2 +

+ By + C =

(2.1)

(2.2)

Conversely, every equation of form (2.2) which has a graph represents a circle or just a single

point. For example,

+ 1 = 0 has no graph, and the graph of x

= 0 is just the

single point (0, 0).

EXAMPLE 2.1

Find the center and radius of the circle x

+ y2 - 2x + 4y - 4 =

Solution

We complete the squares to put the equation in the form (2.1):

- 2x + y2 +4y = 4,

2x + 1 + y2 +4y + 4 = 4 + 1 + 4,

(x - 1)2 +

(y+

2)2 = 9.

The circle has center (1,

-2)

and radius 3.

The graph of

x2 y2

-+-=1

is an ellipse through the points

(±a,

0) and (0,

±b)

(Figure 2.3). If a = b, then the ellipse is

a circle of radius a. If b

> a, then the ellipse is longer in the y-direction.

The curves

x2 y2

- - - = 1 and - - + - = 1

are hyperbolas. The first hyperbola above intersects the x-axis, and the second intersects the

y-axis (Figure 2.4). Both hyperbolas approach the asymptotes y =

±~x

as x increases; that

is, the vertical distance between the curve and the asymptote tends to zero as x increases.

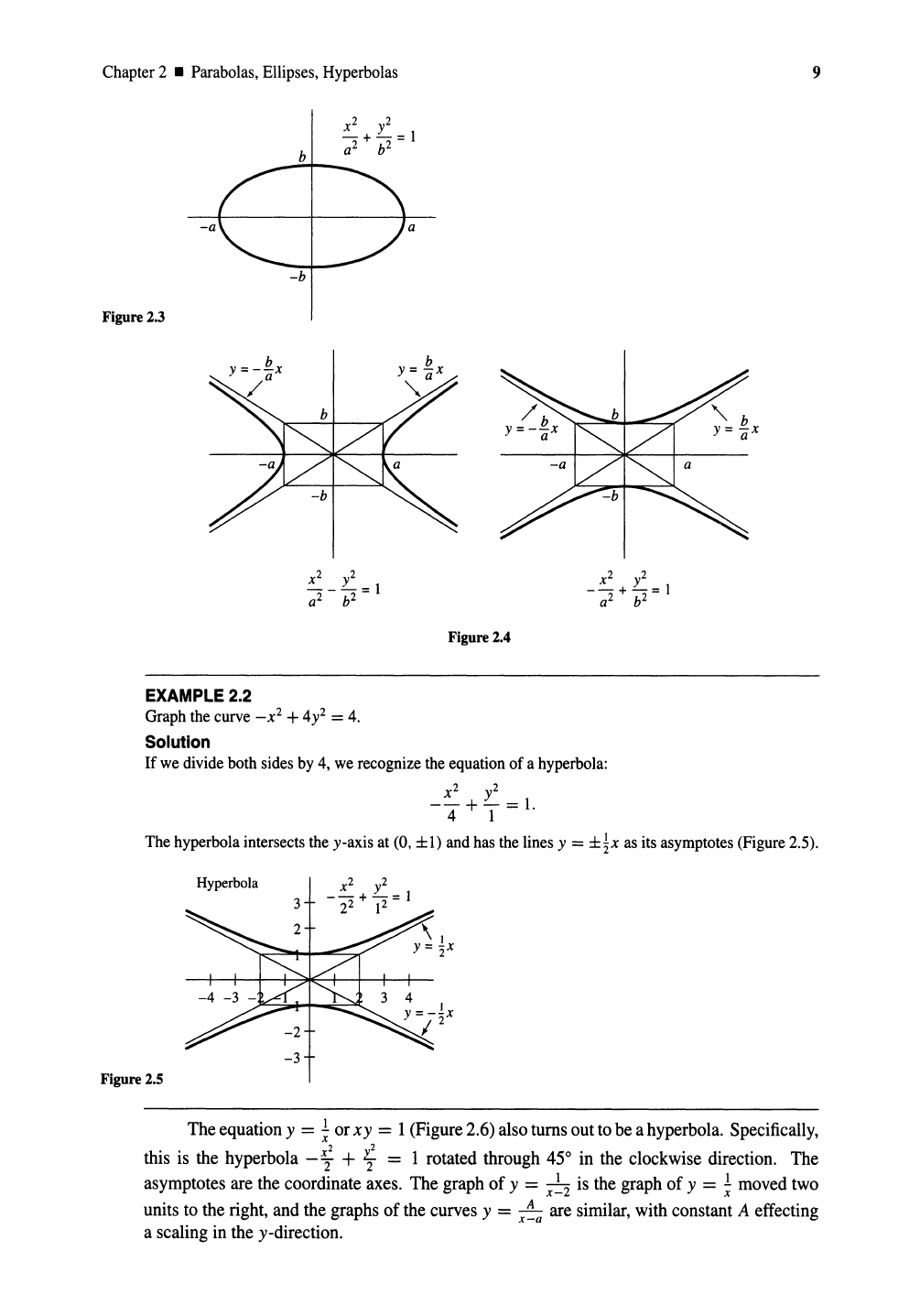
Chapter 2 • Parabolas, Ellipses, Hyperbolas

-a

-b

Figure 2.3

Figure 2.4

EXAMPLE

2.2

Graph the curve

-x

+ 4

2 = 4.

Solution

If we divide both sides by 4, we recognize the equation of a hyperbola:

--+-=1.

4 1

The hyperbola intersects the y-axis at (0,

±l)

and has the lines y =

±!x

as its asymptotes (Figure 2.5).

Hyperbola

Figure 2.5

The equation y =

or xy = 1 (Figure 2.6) also turns out to be a hyperbola. Specifically,

this is the hyperbola -

+ f = 1 rotated through 45° in the clockwise direction. The

asymptotes are the coordinate axes. The graph of

y =

x~2

is the graph of y =

moved two

units to the right, and the graphs of the curves

y =

x~a

are similar, with constant A effecting

a scaling in the y-direction.

Understanding

Calculus

Hyperbola

3 4

Figure 2.6

EXAMPLE

2.3

Findthe equationof the circlewhichpasses throughthe originand the twopoints wherethe linex +y = 1

intersects the circle

+ y2 = 1.

Solution

Any circle has the form x

+ y2 +

+ By + C = 0, so three given points will determine the three

constants

A, B, C. One solution would be to find the two points where x + y = 1 and x

+ y2 = 1

intersect and use these two points and (0, 0) to write three equations in A, B, and C. Here is an easier

way: Any equation

+ y2 - I) +

k(x

+ y - 1) = 0 (*)

is a circle becauseit has the rightform. If a point (xo,

Yo)

satisfiesboth x

+y2

-1

= 0and x +y

-1

= 0,

then it will certainly lie on the circle (*). We find k so the circle (*) also goes through (0, 0),

(

-0

1) + k(0 +0 - 1),

=-1.

Therefore, the sought-forcircle is

+ y2 - I - (x + y - 1) =0,

+ y2 - X - Y =

PROBLEMS

Graph the following curves.

2.1 y =

-x

2.2 y = 2x

1 2

2.3 y =

"2x

2.4 y = (x + 1)2

2.5 y = x

+ 1

2.6 y = 1 - x

2.7 y = x

- 2x +2

2.8 y =

-x

+2x

2.9 x

+ y2 = 4

2.10 (x - 1)2 + y2 = 1

2.11 x

+ y2 - 4y - 5 =0

x2 y2

2.12 - + - = 1

9 4

2.13 x

+ -

2.14 4x

+9y2 =36

Chapter 2 • Parabolas, Ellipses, Hyperbolas 11

2.15 x

= 1

2.16

- x

= 1

2.17 xy = 2

2.18 y

=--

x-I

2.19 Find the equation of the circle which passes through the origin and the two points where

y = 4x - 1 intersects the circle x

+ y2 =4.

2.20 Find the parabola through the point

(-4,3)

and the two points where the line y = x + 1

intersects the parabola

y =x

2.21 Show that the set of points

(x,

y) such that the distance from

(x,

y) to (c, 0) plus the distance

from (x,

y) to

(-c,

0) equals 2a is the ellipse 5+

a2~c2

= 1.

Hint:

Put the square roots

on opposite sides of the equation and square both sides. Isolate the remaining square root

and square both sides again.

22.

r;:;--;

2.22 Show that the top part

the hyperbola

= 1 (i.e., the curve y = by

- 1 =

~Jx2

- a

approaches the asymptote y =

as x

00.

Hint:

To show

x -

0, multiply and divide by x +

and let x

00.

Differentiation

If s(r) is the positionat time t of a car

moving

along a straightroad, then the

average

speed

overthe distancefrom

s(to) to

s(t)

is the distance traveled dividedby the elapsedtime:

s(t)

- s(to)

average

speed = .

t - to

If the speed of the car is not constant, then the

average

speed may have little to do with the

actualspeedat anygiventime.

However,

if thetimeinterval[to, t] is verysmall,thenthespeed

willnot varymuchoverthe interval, and the actualspeedat anygiventimewillbe closeto the

average

speed. We define the speed at a particulartime to, the instantaneous speed at to, to

be the limit of the average speedsover smallerand smallertime intervals [to, t]. This limitis

denoteds' (to), and we write

'(t

) -

1·

s(t)

- s(to)

So-1m

t-Ho

t - to

(3.1)

The numbers'(to) is calledthe derivative of s with respect to t at to, or the rate of change

of s with respect to t at to.

EXAMPLE 3.1

The distance s in feet which a falling object travels in t seconds is approximately s = 16t

•

(This

formula holds for the first few seconds, and then air resistance takes over. Falling bodies do not make

sonic booms.) The distance traveled between

=2 seconds and a subsequent time t is

s(t)

s(2)

= 16t

- 16 . 2

= 16(t

=16(t +

2)(t

- 2).

Hence, the average speed over the time interval [2, t] is

s(t)

s(2)

16(t

2)(t

- 2) 16 2

---=

(t+),

t-2

UnderstandingCalcuIus

and the instantaneous speed at t = 2 is

s'(2)

= lim

s(t)

s(2)

t~2

1 - 2

= lim

16(1

+2) = 64.

t~2

Since s is measuredin feet and 1 in seconds,the speed at t = 2 is 64 ft/sec.

Nowconsiderwhatthe derivative of a functionmeansin a purely geometricsetting. We

look at the function

y =

f(x)

whosegraph is the parabolashownin Figure 3.1. The

changein y over the intervalfrom 1to a nearbypoint x is

f(x)

f(1)

~X2

• 1 =

~(x

l)(x

- 1).

Hence,the averagerate of change of y over this intervalis

f(x)

f(l)

!(x

+ 1)(x - 1) 1

----

= =

-(x

+ 1).

x-I

The abovequotient

(f(x)

f(I»/(x

- 1) is the slope

m(x)

of the secantlinejoining the two

points

(1, !)and (x,

~x2).

The derivative,

f'(l),

is thereforethe limitingslopeof these secant

lines:

f'(I)

= lim

m(x)

x~l

. 1 1

-(x

+ 1) = .

x~12

We define the tangent line to the curve at (1, !)to be the line that has this limiting slope 1.

Hence,the tangentline to y

= !x

at (1,

y - - = 1 . (x - 1).

m =1

Figure 3.1

(3.2)

Now we have these two waysto interpretthe derivative

'( ) - li

f(x)

- f(xo) ·

Xo -

x~xo

X - Xo

(xo) is the rate of changeof f withrespectto x (or of y withrespectto x if y = f

(x»,

andis

also the slopeof the tangentline to y

f(x)

at xo. The expression

(f(x)

!(xo»/(x

- xo)

is the difference quotient for f at xo.

In the precedingexamples, we used the following two obviouslimits:

lim 16(t +2) = 64; lim

-(x

+ 1) = 1.

t~2

x~l

The meaningof the limitconceptis as

follows:

a functionq (x) (suchas the differencequotient

(3.2»

approaches a limit L as x approaches xo, written

limx~xo

q(x)

= L, provided that

q (x) is arbitrarily closeto L forallx sufficiently closeto xo. Thephrases"arbitrarilyclose"and

Chapter 3 • Differentiation

"sufficiently close" can be made arithmetically precise as follows:

limx~xo

(x)

= L provided

that for any given positive number

e (an arbitrary choice of closeness) there corresponds a

positive number 8 (this is how close "sufficiently close" is) such that

q(x)

is within e of L if x

is within 8 of XQ. The intuitive idea of q

(x)

approaching L as a limiting value as x approaches

XQ will suffice for the limits we deal with in this course.

The following examples show some more limits in action, and the action is again the

calculation of derivatives.

EXAMPLE

3.2

Find

f'(-I)

f(x)

= 3x

•

Solution

f'(-I)

= lim

f(x)

fe-I)

x~-I

x-(-I)

3 . 1

lim

---

x~-l

X + 1

= lim 3(x + I)(x - 1)

x~-l

X + 1

= lim 3(x - 1) =

-6.

x~-l

EXAMPLE

3.3

Find

f'(4)

f(x)

Solution

f'(4)

= lim

f(x)

f(4)

x~4

x - 4

= lim

~-J4

x~4

x - 4

= lim

2)(~

+ 2)

x~4

(x -

4)(~

+ 2)

x-4

=lim-----

x~4

(x -

4)(~

+ 2)

lim_

=~.

x~4

EXAMPLE 3.4

Find the equation of the line tangent to

y =

at x = - 2.

Solution

The slope we want is

(- 2) where f

(x)

3 3

f'(-2)

= lim x- =2

x~-2

X -

(-2)

= lim x 2

x~-2

X + 2

= lim 3(2 + x)

x~-2

2x(x

+2)

= lim

-~.

x~-2

2x 4

16 Understanding Calculus

The equation of the tangent line at (- 2, -

y +

= (

-D

(x +2).

EXAMPLE

3.5

Find

f'(4)

f(x)

Solution

+ ! - (J4+

, • x 4

f (4) = hm

------

x~4

X - 4

(Ji

J4)

= lim x 4

x~4

X - 4

(Ji

- J4)(Ji +

J4)

4 - x )

= 1m

+---

x~4

(x -

4)(Ji

J4)

4x(x

- 4)

=!~CX-4;(~+J4)

4~)

1 1 3

---

4 16 16

Notice that in Example 3.5 we effectively found the derivatives of

JXand

separately

and then added the results. That is because the difference quotient for

can be separated

into two groups, one group being the difference quotient for

and the other being the

difference quotient for

EXAMPLE

3.6

A ball thrown downward with an initial speed of 32 ft/sec from the top of a tall building travels a vertical

distance of

s feet in t seconds, where s = 16t

+321. What is its speed at t = I?

Solution

We are asked to find s' (1), and again we separate the difference quotient into the difference quotient for

16t

and that for 32t.

s' (1) = lim

s(t)

s(l)

t~l

t-l

= lim 16t

+ 32t - (16 + 32)

t~l

t - 1

. [16t

-16

32t -

32]

=hm

+---

t~J

t - 1 t - 1

. [16(t + 1)(t - 1) 32(t -

1)]

=hm

+---

t~l

t - 1 t - I

= lim[16(t + 1) + 32] = 64.

t~l

PROBLEMS

Find

f'(a)

for the specified a.

3.1

f(x)

= 2x

;

a = 1

3.2

f(x)

-5x

; a =

-2