Bar-Meir G. Fundamentals of Compressible Fluid

Подождите немного. Документ загружается.

9.7. ISOTHERMAL FLOW EXAMPLES 171

and the density is

ρ =

1, 000, 000

287 ×300

= 11.61

The velocity at the entrance should be

U = M ∗ c = 0.08528 ×347.2

∼

29.6

sec

The diameter should be

D =

4 ˙m

πUρ

4 ×0.2

π × 29.6 × 11.61

∼

0.027

Nevertheless, for the sake of the exercise the other parameters will be calculated. This

situation is reversed question. The ﬂow rate is given with the diameter of the pipe. It

should be noted that the ﬂow isn’t choked.

End solution

Example 9.3:

A gas ﬂows of from a station (a) with pressure of 20[bar] through a pipe with 0.4[m]

diameter and 4000 [m] length to a diﬀerent station (b). The pressure at the exit (station

(b)) is 2[bar]. The gas and the sounding temperature can be assumed to be 300 K.

Assume that the ﬂow is isothermal, k=1.4, and the average friction f=0.01. Calculate

the Mach number at the entrance to pipe and the ﬂow rate.

Solution

First, the information whether the ﬂow is choked needs to be found. Therefore, at ﬁrst

it will be assumed that the whole length is the maximum length.

4fL

max

4 ×0.01 × 4000

0.4

= 400

with

4fL

max

= 400 the following can be written

4fL

∗T

0.0419 400.72021 0.87531 20.19235 20.19235 12.66915

From the table M

≈ 0.0419 ,and

∗T

≈ 12.67

∗T

∼

12.67

' 2.21[bar]

172 CHAPTER 9. ISOTHERMAL FLOW

The pressure at point (b) by utilizing the isentropic relationship (M = 1) pressure ratio

is 0.52828.

∗T

= 2.21 × 0.52828 = 1.17[bar]

As the pressure at point (b) is smaller than the actual pressure P

∗

< P

than the actual

pressure one must conclude that the ﬂow is not choked. The solution is an iterative

process.

1. guess reasonable value of M

and calculate

4fL

2. Calculate the value of

4fL

by subtracting

4fL

−

4fL

3. Obtain M

from the Table ? or by using the Potto–GDC.

Calculate the pressure, P

bear in mind that this isn’t the real pressure but based

on the assumption.

Compare the results of guessed pressure P

with the actual pressure and choose

new Mach number M

accordingly.

Now the process has been done for you and is provided in ﬁgure ??? or in the table

obtained from the provided program.

4fL

max

4fL

0.0419 0.59338 400.32131 400.00000 0.10000

The ﬂow rate is

˙m = ρAMc =

√

π × D

M =

2000000

√

1.4

√

300 ×287

π × 0.2

× 0.0419

' 42.46[kg/sec]

End solution

In this chapter, there are no examples on isothermal with supersonic ﬂow.

9.8 Unchoked situations in Fanno Flow

Table -9.2. The ﬂow parameters for unchoked ﬂow

4fL

max

4fL

0.7272 0.84095 0.05005 0.05000 0.10000

0.6934 0.83997 0.08978 0.08971 0.10000

9.8. UNCHOKED SITUATIONS IN FANNO FLOW 173

Table -9.2. The ﬂow parameters for unchoked ﬂow (continue)

4fL

max

4fL

0.6684 0.84018 0.12949 0.12942 0.10000

0.6483 0.83920 0.16922 0.16912 0.10000

0.5914 0.83889 0.32807 0.32795 0.10000

0.5807 0.83827 0.36780 0.36766 0.10000

0.5708 0.83740 0.40754 0.40737 0.10000

One of the interesting feature of the isothermal ﬂow is that Reynolds number remains

constant during the ﬂow for an ideal gas material (enthalpy is a function of only the

temperature). This fact simpliﬁes the calculation of the friction factor. This topic has

more discussion on the web than on “scientiﬁc” literature. Here is a theoretical example

for such calculation that was discussed on the web.

Example 9.4:

Air ﬂows in a tube with 0.1[m] diameter and 100[m] in length. The relative roughness,

²/D = 0.001 and the entrance pressure is P

= 20[Bar] and the exit pressure is

= 1[Bar] . The surroundings temperature is 27

◦

C. Estimate whether the ﬂow is

laminar or turbulent, estimate the friction factor, the entrance and exit Mach numbers

and the ﬂow rate.

Solution

The ﬁrst complication is the know what is ﬂow regimes. The process is to assume that

the ﬂow is turbulent (long pipe). In this case, for large Reynolds number the friction

factor is about 0.005. Now the iterative procedure as following;

Calculate the

4fL

4 ×0.005 × 100

0.1

= 20

For this value and the given pressure ratio the ﬂow is choked. Thus,

4fL

∗

0.17185 20.0000 4.9179 3.1460 4.9179 0.88017

For this iteration the viscosity of the air is taken from the Basics of Fluid Mechanics by

this author and the Reynolds number can be calculated as

Re =

D U ρ

0.1 ×0.17185 ×

√

1.4 ×287 × 300 ×

200000

287 ×300

0.0008

∼ 17159.15

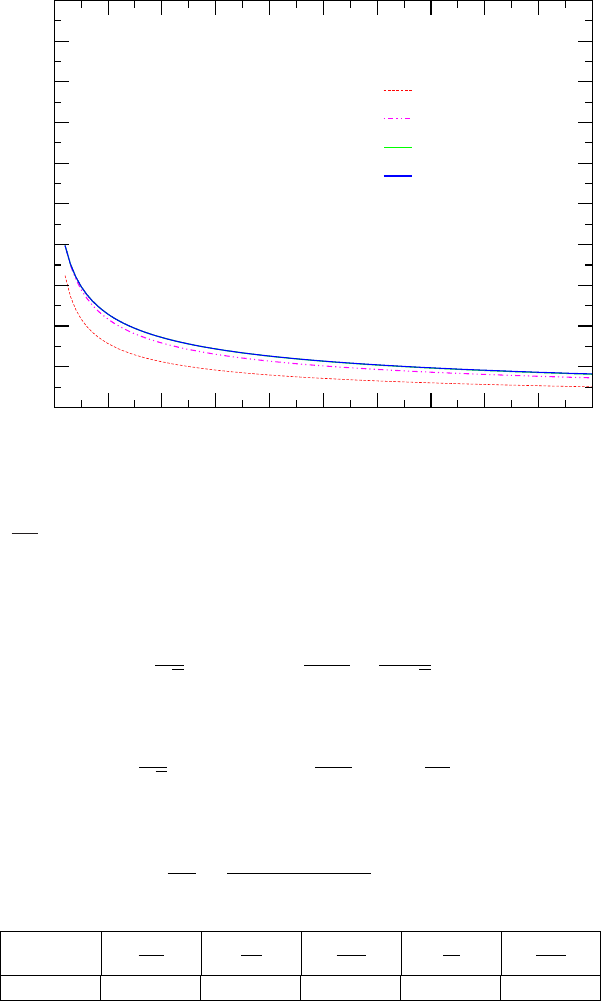
174 CHAPTER 9. ISOTHERMAL FLOW

0 10 20 30 40

50 60

70 80 90 100



4fL

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

/ P

= 0.8

/ P

= 0.5

/ P

= 0.2

/ P

= 0.10

isothermal flow

Fri Feb 25 17:20:14 2005

Fig. -9.3. The Mach number at the entrance to a tube under isothermal ﬂow model as a

function

4fL

For this Reynolds number the ﬁction factor can be estimated by using the full

Colebrook’s equation

√

= −2 log

ε/D

3.7

2.51

√

(9.55)

or the approximated Haaland’s equation

√

= −1.8 log

ε/D

3.7

1.11

6.9

(9.56)

which provide f = 0.0053 and it is a reasonable answer in one iteration. Repeating

the iteration results in

4fL

4 ×0.0053 × 100

0.1

= 21.2

with

4fL

∗

0.16689 21.4000 5.0640 3.2357 5.0640 0.87987

9.8. UNCHOKED SITUATIONS IN FANNO FLOW 175

And the “improved” Reynolds number is

Re =

0.1 ×0.16689 ×

√

1.4 ×287 × 300 ×

200000

287 ×300

0.0008

∼ 16669.6

And the friction number is .0054 which very good estimate compare with the assumption

that this model was built on.

End solution

176 CHAPTER 9. ISOTHERMAL FLOW

CHAPTER 10

Fanno Flow

c.v.

flow

direction

No heat transer

Fig. -10.1. Control volume of the gas ﬂow in a con-

stant cross section

An adiabatic ﬂow with friction is

named after Ginno Fanno a Jewish

engineer. This model is the second

pipe ﬂow model described here. The

main restriction for this model is that

heat transfer is negligible and can be

ignored

. This model is applica-

ble to ﬂow processes which are very

fast compared to heat transfer mech-

anisms with small Eckert number.

This model explains many in-

dustrial ﬂow processes which includes emptying of pressured container through a rel-

atively short tube, exhaust system of an internal combustion engine, compressed air

systems, etc. As this model raised from need to explain the steam ﬂow in turbines.

10.1 Introduction

Consider a gas ﬂowing through a conduit with a friction (see Figure (10.1)). It is

advantages to examine the simplest situation and yet without losing the core properties

of the process. Later, more general cases will be examined

Even the friction does not convert into heat

Not ready yet, discussed on the ideal gas model and the entry length issues.

177

178 CHAPTER 10. FANNO FLOW

10.2 Fanno Model

The mass (continuity equation) balance can be written as

˙m = ρAU = constant (10.1)

,→ ρ

= ρ

The energy conservation (under the assumption that this model is adiabatic

ﬂow and the friction is not transformed into thermal energy) reads

= T

(10.2)

,→ T

= T

(10.3)

Or in a derivative from

dT + d

= 0 (10.4)

Again for simplicity, the perfect gas model is assumed

P = ρRT (10.5)

,→

It is assumed that the ﬂow can be approximated as one–dimensional. The force

acting on the gas is the friction at the wall and the momentum conservation reads

−AdP − τ

= ˙mdU (10.6)

It is convenient to deﬁne a hydraulic diameter as

4 ×Cross Section Area

wetted perimeter

(10.7)

Or in other words

A =

πD

(10.8)

The equation of state is written again here so that all the relevant equations can be found when

this chapter is printed separately.

10.3. NON–DIMENSIONALIZATION OF THE EQUATIONS 179

It is convenient to substitute D for D

and yet it still will be referred to the same

name as the hydraulic diameter. The inﬁnitesimal area that shear stress is acting on is

= πDdx (10.9)

Introducing the Fanning friction factor as a dimensionless friction factor which is some

times referred to as the friction coeﬃcient and reads as the following:

f =

ρU

(10.10)

By utilizing equation (10.2) and substituting equation (10.10) into momentum equation

(10.6) yields

−

z}|{

πD

dP − πDdx

z }| {

ρU

= A

˙m

z}|{

ρU dU (10.11)

Dividing equation (10.11) by the cross section area, A and rearranging yields

−dP +

4fdx

ρU

= ρUdU (10.12)

The second law is the last equation to be utilized to determine the ﬂow direction.

≥ s

(10.13)

10.3 Non–Dimensionalization of the Equations

Before solving the above equation a dimensionless process is applied. By utilizing the

deﬁnition of the sound speed to produce the following identities for perfect gas

k RT

|{z}

(10.14)

Utilizing the deﬁnition of the perfect gas results in

ρU

(10.15)

Using the identity in equation (10.14) and substituting it into equation (10.11) and

after some rearrangement yields

−dP +

4fdx

kP M

ρU

dU =

ρU

z }| {

kP M

(10.16)

180 CHAPTER 10. FANNO FLOW

By further rearranging equation (10.16) results in

−

4fdx

= kM

(10.17)

It is convenient to relate expressions of (dP/P ) and dU/U in terms of the Mach

number and substituting it into equation (10.17). Derivative of mass conservation

((10.2)) results in

dρ

z }| {

= 0 (10.18)

The derivation of the equation of state (10.5) and dividing the results by equation of

state (10.5) results

dρ

(10.19)

Derivation of the Mach identity equation (10.14) and dividing by equation (10.14)

yields

d(M

)

d(U

)

−

(10.20)

Dividing the energy equation (10.4) by C

and by utilizing the deﬁnition Mach number

yields

(k − 1)

| {z }

,→

(k − 1)

kRT

|{z}

,→

k − 1

= 0 (10.21)

Equations (10.17), (10.18), (10.19), (10.20), and (10.21) need to be solved. These

equations are separable so one variable is a function of only single variable (the chosen

as the independent variable). Explicit explanation is provided for only two variables,

the rest variables can be done in a similar fashion. The dimensionless friction,

4fL

is chosen as the independent variable since the change in the dimensionless resistance,

4fL

, causes the change in the other variables.

Combining equations (10.19) and (10.21) when eliminating dT/T results

dρ

−

(k − 1)M

(10.22)