Bar-Meir G. Fundamentals of Compressible Fluid

Подождите немного. Документ загружается.

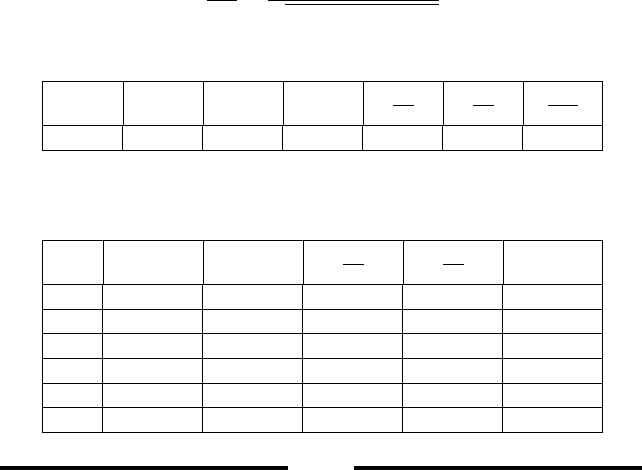
7.2. DIFFUSER EFFICIENCY 151

Thus the static Mach number, M

502.25

√

1.091 ×143 × 350

∼ 2.15

With this value for the Mach number Potto-GDC provides

2.9222 0.47996 2.1500 0.0 2.589 9.796 0.35101

This table was obtained by using the procedure described in this book. The iteration

of the procedure are

i M

0 3.1500 0.46689 2.8598 11.4096 0.0

1 2.940 0.47886 2.609 9.914 0.0

2 2.923 0.47988 2.590 9.804 0.0

3 2.922 0.47995 2.589 9.796 0.0

4 2.922 0.47996 2.589 9.796 0.0

5 2.922 0.47996 2.589 9.796 0.0

End solution

152 CHAPTER 7. NORMAL SHOCK IN VARIABLE DUCT AREAS

CHAPTER 8

Nozzle Flow With External Forces

This chapter is under heavy construction. Please ignore. If you want to

contribute and add any results of experiments, to this chapter, please do so.

You can help especially if you have photos showing these effects.

In the previous chapters a simple model describing the ﬂow in nozzle was ex-

plained. In cases where more reﬁned calculations have to carried the gravity or other

forces have to b e taken into account. Flow in a vertical or horizontal nozzle are diﬀerent

because the gravity. The simpliﬁed models that suggests them–self are: friction and

adiabatic, isothermal, seem the most applicable. These models can served as limiting

cases for more realistic ﬂow.

The eﬀects of the gravity of the nozzle ﬂow in two models isentropic and

isothermal is analyzed here. The isothermal nozzle model is suitable in cases where

the ﬂow is relatively slow (small Eckert numbers) while as the isentropic model is more

suitable for large Eckert numbers.

The two models produces slightly diﬀerent equations. The equations results in

slightly diﬀerent conditions for the chocking and diﬀerent chocking speed. Moreover,

the working equations are also diﬀerent and this author isn’t aware of material in the

literature which provides any working table for the gravity eﬀect.

153

154 CHAPTER 8. NOZZLE FLOW WITH EXTERNAL FORCES

8.1 Isentropic Nozzle (Q = 0)

The energy equation for isentropic nozzle provides

dh + U dU =

external work

potential

diﬀerence, i.e.

z × g

z }| {

f(x)dx (8.1)

Utilizing equation (5.27) when ds = 0 leads to

+ UdU = f(x

)dx

(8.2)

For the isentropic process dP = const × kρ

k−1

dρ when the const = P/ρ

any point of the ﬂow. The equation (8.2) becomes

z }| {

any point

z}|{

dρ

+ UdU = k

z}|{

dρ

UdU =f (x

)dx

(8.3)

kRT dρ

+ UdU =

dρ + U dU =f(x

)dx

The continuity equation as developed earlier (mass conservation equation isn’t

eﬀected by the gravity)

−

dρ

= 0 (8.4)

Substituting dρ/ρ from equation 8.3, into equation (8.2) moving dρ to the right hand

side, and diving by dx

yields

= c

+ f(x

) (8.5)

Rearranging equation (8.5) yields

f(x

)

(8.6)

And further rearranging yields

1 −M

f(x

)

(8.7)

8.1. ISENTROPIC NOZZLE (Q = 0) 155

Equation (8.7) can be rearranged as

(1 −M

)

f(x

)

(8.8)

Equation (8.8) dimensionless form by utilizing x = x

/` and ` is the nozzle length

(1 −M

)







`f(x)

c cM

|{z}







(8.9)

And the ﬁnal form of equation (8.9) is

(1 −M

)

`f(x)

(8.10)

The term

`f(x)

is considered to be very small (0.1 × 10/100000 < 0.1%) for

“standard” situations. The dimensionless number,

`f(x)

sometimes referred as Ozer

number determines whether gravity should be considered in the calculations. Neverthe-

less, one should be aware of value of Ozer number for large magnetic ﬁelds (astronomy)

and low temperature, In such cases, the gravity eﬀect can be considerable.

As it was shown before the transition must occur when M = 1. Consequently,

two zones must be treated separately. First, here the Mach number is discussed and

not the pressure as in the previous chapter. For M < 1 (the subsonic branch) the term

(1−M

)

is positive and the treads determined by gravity and the area function.

`f(x)

> 0 =⇒ d(M

) > 0

or conversely,

`f(x)

< 0 =⇒ d(M

) < 0

For the case of M > 1 (the supersonic branch) the term

(1−M

)

is negative and

therefore

`f(x)

> 0 =⇒ d(M

) < 0

For the border case M = 1, the denominator 1 − M

= 0, is zero either d(M

) = ∞

`f(x)

= 0.

156 CHAPTER 8. NOZZLE FLOW WITH EXTERNAL FORCES

And the dM is indeterminate. As it was shown in chapter (5) the ﬂow is chocked

(M = 1) only when

`f(x)

= 0. (8.11)

It should be noticed that when f(x) is zero, e.g. horizontal ﬂow, the equation

(8.11) reduced into

= 0 that was developed previously.

The ability to manipulate the location provides a mean to increase/decrease

the ﬂow rate. Yet this ability since Ozer number is relatively very small.

This condition means that the critical point can occurs in several locations that

satisﬁes equation (8.11). Further, the critical point, sonic point is

6= 0 If f(x) is

a positive function, the critical point happen at converging part of the nozzle (before

the throat) and if f(x) is a negative function the critical point is diverging part of the

throat. For example consider the gravity, f(x) = −g a ﬂow in a nozzle vertically the

critical point will be above the throat.

8.2 Isothermal Nozzle (T = constant)

CHAPTER 9

Isothermal Flow

In this chapter a mo del dealing with gas that ﬂows through a long tube is described.

This model has a applicability to situations which occur in a relatively long distance

and where heat transfer is relatively rapid so that the temperature can be treated, for

engineering purposes, as a constant. For example, this model is applicable when a

natural gas ﬂows over several hundreds of meters. Such situations are common in large

cities in U.S.A. where natural gas is used for heating. It is more predominant (more

applicable) in situations where the gas is pumped over a length of kilometers.

c.v.

flow

direction

Fig. -9.1. Control volume for isothermal ﬂow.

The high speed of the gas is

obtained or explained by the combi-

nation of heat transfer and the fric-

tion to the ﬂow. For a long pipe, the

pressure diﬀerence reduces the density

of the gas. For instance, in a perfect

gas, the density is inverse of the pres-

sure (it has to be kept in mind that

the gas undergoes an isothermal pro-

cess.). To maintain conservation of mass, the velocity increases inversely to the pressure.

At critical point the velocity reaches the speed of sound at the exit and hence the ﬂow

will be choked

This explanation is not correct as it will be shown later on. Close to the critical point (about, 1/

√

the heat transfer, is relatively high and the isothermal ﬂow model is not valid anymore. Therefore,

the study of the isothermal ﬂow above this point is only an academic discussion but also provides the

upper limit for Fanno Flow.

157

158 CHAPTER 9. ISOTHERMAL FLOW

9.1 The Control Volume Analysis/Governing equations

Figure (9.1) describes the ﬂow of gas from the left to the right. The heat transfer up

stream (or down stream) is assumed to b e negligible. Hence, the energy equation can

be written as the following:

˙m

= c

dT + d

= c

(9.1)

The momentum equation is written as the following

−AdP − τ

wetted area

= ˙mdU (9.2)

where A is the cross section area (it doesn’t have to be a perfect circle; a close enough

shape is suﬃcient.). The shear stress is the force per area that acts on the ﬂuid by

the tube wall. The A

wetted ar ea

is the area that shear stress acts on. The second law

of thermodynamics reads

− s

= ln

−

k − 1

(9.3)

The mass conservation is reduced to

˙m = constant = ρU A (9.4)

Again it is assumed that the gas is a perfect gas and therefore, equation of

state is expressed as the following:

P = ρRT (9.5)

9.2 Dimensionless Representation

In this section the equations are transformed into the dimensionless form and presented

as such. First it must b e recalled that the temperature is constant and therefore,

equation of state reads

dρ

(9.6)

It is convenient to deﬁne a hydraulic diameter

4 ×Cross Section Area

wetted perimeter

(9.7)

9.2. DIMENSIONLESS REPRESENTATION 159

Now, the Fanning friction factor

is introduced, this factor is a dimensionless friction

factor sometimes referred to as the friction coeﬃcient as

f =

ρU

(9.8)

Substituting equation (9.8) into momentum equation (9.2) yields

−dP −

4dx

ρU

˙m

z}|{

ρU dU (9.9)

Rearranging equation (9.9) and using the identify for perfect gas M

= ρU

/kP yields:

−

4fdx

kP M

(9.10)

Now the pressure, P as a function of the Mach number has to substitute along with

velocity, U .

= kRT M

(9.11)

Diﬀerentiation of equation (9.11) yields

d(U

) = kR

dT + T d(M

)

(9.12)

d(M

)

d(U

)

−

(9.13)

Now it can be noticed that dT = 0 for isothermal process and therefore

d(M

)

d(U

)

2U dU

2dU

(9.14)

The dimensionalization of the mass conservation equation yields

dρ

2UdU

dρ

d(U

)

2 U

= 0 (9.15)

Diﬀerentiation of the isotropic (stagnation) relationship of the pressure (5.11) yields

1 +

k−1

(9.16)

It should be noted that Fanning factor based on hydraulic radius, instead of diameter friction

equation, thus “Fanning f” values are only 1/4th of “Darcy f” values.

160 CHAPTER 9. ISOTHERMAL FLOW

Diﬀerentiation of equation (5.9) yields:

= dT

1 +

k − 1

+ T

k − 1

(9.17)

Notice that dT

6= 0 in an isothermal ﬂow. There is no change in the actual

temperature of the ﬂow but the stagnation temperature increases or decreases depending

on the Mach number (supersonic ﬂow of subsonic ﬂow). Substituting T for equation

(9.17) yields:

k−1

d M

1 +

k−1

(9.18)

Rearranging equation (9.18) yields

(k − 1) M

1 +

k−1

(9.19)

By utilizing the momentum equation it is possible to obtain a relation between

the pressure and density. Recalling that an isothermal ﬂow (T = 0) and combining it

with perfect gas model yields

dρ

(9.20)

From the continuity equation (see equation (9.14)) leads

2dU

(9.21)

The four equations momentum, continuity (mass), energy, state are describ ed

above. There are 4 unknowns (M, T, P, ρ)

and with these four equations the solution is

attainable. One can notice that there are two possible solutions (because of the square

power). These diﬀerent solutions are sup ersonic and subsonic solution.

The distance friction,

4fL

, is selected as the choice for the independent variable.

Thus, the equations need to be obtained as a function of

4fL

. The density is eliminated

from equation (9.15) when combined with equation (9.20) to become

= −

(9.22)

Assuming the upstream variables are known.