Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

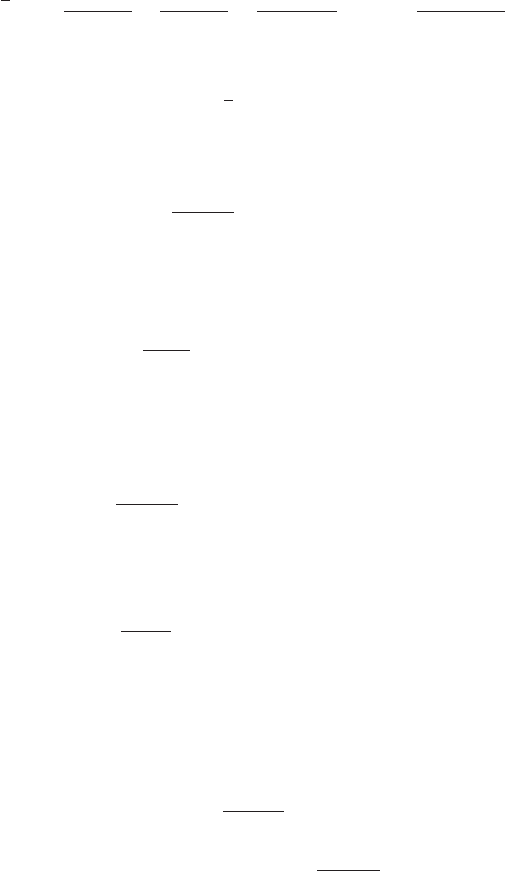
To solve Eq. (G.15), we employ the Laplace transform technique used in
Section 9.3.2. Upon taking the Laplace transform of Eq. (G.15) and rearrang-
ing terms, we obtain
(G.16)
where s is the Laplace transform parameter, Y(0) is the displacement at
h 0, Y(0) is the slope of the string at h 0, the prime denotes the deriva-
tive with respect to h, and is the Laplace transform of Y(h). Using trans-
form pairs 3, 18, and 19 from Table A in Appendix A, the inverse transform
of Eq. (G.16) is
(G.17)
where
(G.18)
and u(h) is the unit step function.
We shall consider only the case where the string is clamped at both ends;
that is, when Y(0) 0 and Y(1) 0. Then Eq. (G.17) simplifies to
(G.19)
To determine Y(0) in Eq. (G.19), we use the boundary condition Y(1) 0.
Then, from Eq. (G.19), we find that
(G.20)
Upon substituting Eq. (G.20) into Eq. (G.19) and collecting terms, we obtain
(G.21)
where
(G.22)
To obtain the frequency equation, we note that Eq. (G.21) must be valid
at h h
1
and at h h
2
. Thus, Eq. (G.21) yields
(G.23)c
1 C
1
1h
1
,
s
2 C
2
1h
1
,
s
2
C
1
1h
2
,
s
2 1 C
2
1h
2
,
s
2
de
Y1h
1
2
Y1h
2
2
f 0
C
2
1h,
s
2 B1h,
s
2 B11,
s
2
sin
s
h
sin
s
C
1
1h,
s
2 A11,
s
2
sin
s
h
sin
s
A1h,
s
2
Y1h 2 C
1
1h,
s
2Y1h
1
2 C
2
1h,
s
2Y1h
2
2
Y¿10 2
s
sin
s
3A11,
s
2Y1h
1
2 B11,
s
2Y1h
2
24
Y1h 2
sin
s
h
s
Y¿10 2 A1h,
s
2Y1h
1
2 B1h,
s
2Y1h
2
2
B1h,
s
2
K
string
s
sin 3
s
1h h
2
24u 1h h
2
2
A1h,
s
2 g
s
s
sin 3
s
1h h
1
24u1h h
1
2
Y1h 2 Y10 2cos
s
h
sin
s
h
s
Y¿10 2 A1h,
s
2Y1h
1
2 B1h,
s
2Y 1h
2
2
Y
1s 2
Y
1s 2
sY10 2
s
2
2
s
Y¿10 2
s
2
2
s
2
s
g
s
e
sh
1
s
2
2
s
Y1h
1
2
K
string
e
sh
2
s
2
2
s
Y1h
2
2
690 APPENDIX G Natural Frequencies and Mode Shapes of Bars, Shafts, and Strings

The frequency equation is obtained by setting the determinant of the coeffi-
cients of Eq. (G.23) to zero, which gives
(G.24)
where
n,s
n 1, 2, . . ., are the natural frequency coefficients. Using Eqs.
(G.22) and noting from Eqs. (G.18) that A(h
1
,
n,s
) 0 and B(h
2
,
n,s
) 0,
we can write Eq. (G.24) as
(G.25)
When the spring and mass are attached at the same location; that is, h
1
h
2
,
we find from Eq. (G.18) that A(h
2
,
n,s
) 0 and B(h
1
,
n,s
) 0. Therefore,
Eq. (G.25) reduces to
(G.26)
The corresponding mode shapes are
(G.27)
when M
o
0 and/or k
string
0. When M
o
0 and k
string
0, we use Eq. (G.19)
to obtain
(G.28)Y
n
1h 2 sin 1
n,s
h2
Y
n
1h 2
C
2
1h
1
,
n,s
2
1 C
1
1h
1
,
n,s
2
C
1
1h,
n,s
2 C
2
1h,
n,s
2
n 1, 2, . . .
sin
n,s
ag
s
n,s
K
string
n,s
bsin
n,s
h
1
sin 3
n,s
11 h
1
24 0
B11,
n,s
23sin
n,s
h
2
A1h
2
,
n,s
2sin
n,s
h
1
4 0
A11,
n,s
23sin
n,s
h
1
B1h
1
,
n,s
2sin
n,s
h
2
4
sin
n,s
31 A1h
2
,
n,s
2B1h
1
,
n,s
24
31 C
1
1h
1
,
n,s
2431 C
2
1h
2
,
n,s
24 C
1
1h
2
,
n,s
2C
2
1h
1
,
n,s
2 0
General Solution for the Vibrations of Bars, Shafts, and Strings 691
TABLE G.4
Natural Frequency Equations and Natural Frequency Coefficients for a String Clamped at Each End with Various Combinations
of In-Span Attachments: M
o
at h h
1
and K
string
at h h
2
.
Case In-Span Attachments Frequency Equation
*
1 None sin
n,s
0 n (n 1,2, . . .)
2
Spring only
—
3
Mass only
—
Mass and spring
4 and
—
Mass and spring
5(M
o
≠ 0, k
string
≠ 0, and
—
h
1
h
2
)
*
In Case 4, see Eqs. (G.18) for the definitions of A(h,
s
) and B(h,
s
).
sin
n,s
0
ag
string
n,s
K
string
n,s
bsin
n,s
h
1
sin 3
n,s
11 h
1
24
B 11,
s
23sin
s
h
2
A1h
2
,
s
2sin
s
h
1
4 0h
1
h
2
2
A11,
s
23sin
s
h
1
B1h
1
,
s
2sin
s
h
2
41M
o
0, k
string
0,
sin
s
31 A1h
2
,
s
2B 1h
1
,
s
24
sin 1
n,s
2
n,s
g
string
sin 1
n,s
h
1
2 sin 1
n,s
31 h
1
42 0
1M
o
0 and k
string
0 2
n,s
sin 1
n,s
2 K
string
sin 1
n,s
h
2
2sin 1
n,s
31 h
2
42 0
1M
o
0 and k
string
0 2
n,s
/p
It is noted from Eqs. (G.18) that when M
o
0, A(h,
s
) 0 and, there-
fore, from Eq. (G.22) we have that C
1
(h,
s
) 0 and that when k
string
0,
B(h,
s
) 0 and, therefore, C
2
(h,
s
) 0.
We shall consider three special cases of these results: (1) M
o
0 and
k
string
0; (2) M
o
0 and k
string
0; and (3) M
o
0 and k
string
0, when
h
1
h
2
and when h
1
h
2
. These special cases simplify the frequency equa-
tion, Eq. (G.25), to the expressions shown in the third column of Table G.4.
692 APPENDIX G Natural Frequencies and Mode Shapes of Bars, Shafts, and Strings

693
Answers to Selected Exercises
Chapter 1
E1.2
E1.5
E1.10
E1.11
E1.17
Chapter 2
E2.2
where
E2.6
k
e
k a
4h
a
b
2
, h 2L
2
1a/22
2
b p w cos
1
a
b a
cosw
r1w 2
b
J
m
l
1b 2 m
l
c
l
2
12
a
l
2
b
2
a
2
al cos 1b 2d
J
m
e
1
3
m
e
e
2
J
m
s
m
s
b
2
J
m
b
1
3
m
b
b
2
J
O¿
J
m
l
1b 2 J
m
s
J
m
b
J
m
e
1
2
m 1r
2
1w
#
u
#
2
2
R
2
u
#
2
2rRu
#
1w
#
u
#
2cosw 2
T
pendulum
1
2
J
O
u
#
2
H 3J
O
u
#
R
2
u
#
r
2
1w
#
u
#
2 rR12u
#
w
#
2cosw 4k
p M
r
r
#
1
e¿
1
1M
bar
L
bar
M
r
r
1
2u
#
e¿
2
a
m
1r
$
1
r
1
u
#
2
2e¿
1
1r
1
u
$
2r
#
1
u
#
2e¿
2
V
m
r
#
1
e¿
1
r
1
u
#
e¿
2
a
P/O
Lu
$
e
1
Lu
#
2
e
2
v
P/O
Lu
#
e
1
694 ANSWERS TO SELECTED EXERCISES
E2.10
where
E2.12
where
E2.16
a)
b) x
0
0.01 m and k
e
100060 N/m.
E2.18 The dual tire relation is
and that for the wide-base tire is
E2.19
Chapter 3
E3.2
E3.3
E3.5
where
E3.10 r
4
o
r
4
i
7.272 10
7
m
4
v
o
B
k
b
m
and k
b
3EI
L
3
v
n
v
o
B
1 11 r/L 2
2
v
2
o
mx
$
cx
#
2kx 0
mx
$
cx
#
kx 0
k
e
2rgA
o
2nA
o
P
o
L
o
F
widebase
149.84 784.18d 6.32d
2
N
F
dualtire
81.85 968.72d 21.8d
2
N
k
e
1k
1
k
2
2 31k
1
k
2
2ax
2
0
k
123
a
1
k
1
k
2
1
k
3
b
1
and
k
56
a
1
k
5
1
k
6
b
1
k
e
k
123
cos
2
u
1
k
4
cos
2
1p u
2
2 k
56
cos
2
1u
3
p2
k
213
k
2
k
13
,
k
13
a
1
k
1
1
k
3
b
1
,
k
1
3E
1
I
1
L
3
,
and
k
2
3E
2
I
2
L
3
,
k
e
a
1
k
213
1
k
4
b
1
Au: We have not
made any correc-
tions in this page,
as the scanned pdf
does not contain
this page.

E3.12 rad/s
E3.14 v
n
15.26 rad/s and z 0.305
E3.19 a) For tap water:
b) For salt water: v
nsw
1.095v
ntw
E3.26
E3.30
where
and
E3.31
a)
b)
E3.34 rad/s
Chapter 4
E4.3
E4.8 u1t2 4.08te
1.25t
rad
x1t 2 0.002sin 1100.24t2
m
v
n
B
2k cos
2
g
m
c
Ld
a
2
21J
o
mL
2
21rpg 2
1J
o
mL
2
2u
$
ca
2
u
#
1
4
pd
2
rgL
2
u 1m m
b
/2 2gL
k
c1
a
1
k
c
1
k
1
b
1
and
k
c
3EI
r
3
m
e
J
c
m
c
r
2
m
r
r
2
J
sp
a
r
L
1
b
2
J
as
a
r
L
1
b
2
k
e
k
c1
r
2
k
2
a
L
2
r
L
1
b
2
k
3
a
L
3
r
L
1
b
2
m
p
g
2
a
r
L
1
b
2
1L
2
L
3
a2 m
a
gL
3
a
r
L
1
b
2
v
n
B
k
e
m
e
z
c
1
c
2
c
3
2mv
n
v
n
B
k
1
k
23
m
,
k
23
a
1
k
2
1
k
3
b
1
v
ntw
B
g
s
w
h
v
n
d
2
4 B
pG
2J
G
L
Answers to Selected Exercises 695

E4.9
E4.12 Mass m
2
separates from mass m
1
since
E4.14 z 0.0367 and v
d
5.288 rad/s
E4.19 For uncracked concrete x
max
0.5429 m and for cracked concrete
x
max
0.5426 m; therefore, the maximum displacement remains virtually un-
changed.
E4.20
E4.29 We notice that the envelope of peak amplitudes does not decay ex-
ponentially. In fact, the decay is linear and, therefore, the system is not vis-
cously damped.
Chapter 5
E5.2 Steady-state amplitude is 1.9 mm and the phase is 0.882 radians.
E5.5 rad/s
E5.11
E5.12
E5.13 c 61.52 10
3
Ns/m and the dynamic force transmitted to the base
is 48 N
E5.16 One possible value is k
2
288 kN/m for g 1.8 from Figure 5.36a,
which gives a TR 0.0229 0.08.
E5.17 h
block
1.965 m
E5.19 c
eq
15.9 Ns/m
Chapter 6
E6.2 x1t 2
1
1.73
3e
t
sin 11.73t 2u1t2 e
1t52
sin 11.733t 5 42u1t 5 24
G1jv2
3cv
2
jvk
k mv
2
3cjv
v
2
31.32
2
a
o
0.028/1m m
o
2 a
o
v
n
B
v
r
2
1k
1
k
2
2L
2
J
0
x1t 2 1.67e
0.9048t
sin 175.39t 0.642 2 mm
g
X
o
v
2
n
0.981 1
d
2pz
21 z
2
696 ANSWERS TO SELECTED EXERCISES

E6.7
where
E6.8
where t v
n
t.
E6.11
where
and v
d
3.98 rad/s and w 1.47 radians.
Chapter 7
E7.6
E7.8
E7.9
E7.13
E7.16
£
J
1
00
0 J
ˆ
3
J
2
0
00J
ˆ
4
§•
w
$
1
wˆ
$
2
wˆ
$
4
¶ £
k
t1
k
t1
0
k
t1
k
t1
k
ˆ
t2
k
ˆ
t2
0 k
ˆ
t2
k
ˆ
t2
§•
w
1
w
ˆ
2
w
ˆ
4
¶ •
0
0
0
¶
1J
G
ml
2
2u
$
mlx
$
cos u k
t
u mgl cos u
mx
$
mlu
$
cos u mlu
#
2
sin u kx mg
c
m
1
0
0 m
2
de
x
$
1
x
$
2
f c
1c
1
c
2
2 0
00
de
x
#
1
x
#
2
f c
k
1
k
4
k
2
k
3
k
2
k
3
k
2
k
3
k
2
k
3
de
x
1
x
2
f e
0
0
f
c
M m 0
0 ml
2
de
x
$
ˆ
w
$
ˆ
f c
c 0
0 c
t
de
x
#
ˆ
w
#
ˆ
f c
k 0
0 mgl
de
x
ˆ
w
ˆ
f e
F
o
cos vt
0
f
c
m
1
0
0 m
2
de
x
$
1
x
$
2
f c
k
1
k
2
k
2
k
2
k
2
de
x
#
1
x
#
2
f c
c
1
c
2
c
2
c
2
c
2
de
x
1
x
2
f e
c
1
x
#
3
k
1
x
3
0
f
g1t 2 1
e
zv
n
t
21 z
2
sin 1v
d
t w2
x1t 2
f
o
k
3g1t2u1t 2 g1t t
o
2u1t t
o
24
2.2211
cos 1t 3.54 22u1t 3.54 2
m
x1t 2 0.471t sint 2u1t2 0.161t sin 1t 3.542 3.54 cos 1t 3.5422u1t 3.542
G1s 2
F
o
sk
12z s 2x102 x
#
10 2
X1s 2
G1s 21g 2g
c
zs2
2g
c
zs
3
1g 4g
c
z
2
2s
2
12g
c
z11 g 2 2zg2s g
Answers to Selected Exercises 697
E7.19
a)
b)
c)
E7.26 The natural frequencies of the system are
and the corresponding modal matrix is
E7.28 v
1
316.2 rad/s, v
2
2024.8 rad/s and
E7.29 v
1
1.246 rad/s, v
2
2.557 rad/s and
E7.37
1
0.835,
1
2.07, and the mode shape ratios are
E7.51 The modal damping factors are z
1
1.466 and z
1
1.689 and the
modal mass matrix and modal stiffness matrix are, respectively,
3M
D
4 c
40
04
d
and
3K
D
4 c
1.712 0
0 6.828
d
X
o1
L®
o1
3.3
and
X
o2
L®
o2
0.303
5X6
1
e
0.694
1
f
and
5X6
2
e
0.288
1
f
5Y6
1
e
0.513
1
f
and
5Y6
2
e
22.27
1
f
£ c
0.991 0.131
0.131 0.991
d
and
v
2
1.326
B
k
m
v
1
1.114
B
k
m
m
2
x
$
2
k
4
k
3
k
3
k
4
x
2
0
m
1
x
$
1
k
1
k
2
k
1
k
2
x
1
0
m
2
x
$
2
k
4
x
2
k
4
L
2
1a
1
k
2
L
1
x
1
a
1
k
4
L
2
x
2
2 0
m
1
x
$
1
k
2
x
1
k
2
L
1
1a
1
k
2
L
1
x
1
a
1
k
4
L
2
x
2
2 0
J
O
u
$
11k
1
k
2
2L
2
1
1k
3
k
4
2L
2
2
2u k
2
L
1
x
1
k
4
L
2
x
2
0
m
2
x
$
2
k
4
x
2
k
4
L
2
u 0
m
1
x
$
1
k
2
x
1
k
2
L
1
u 0
698 ANSWERS TO SELECTED EXERCISES
Chapter 8
E8.3 The response of mass m
1
is
and that of mass m
2
is
E8.8
E8.9
where
E8.10
where
E8.22
k
1
G
22
1j2
1 m
r
v
2
r
2
m
r
D
o
k
1
G
12
1j2
v
2
r
D
o
v
v
o
and
v
o
B
3EI
mL
3
•
Y
1
Y
2
Y
3
¶
F
2
mv
2
o
C
1 27
2
14
2
4
2
14
2
1 8
2
2.5
2
4
2
2.5
2
1
2
S
1
•
14
8
2.5
¶
v
n1
B
k
t1
J
1
,
v
n2
B
k
t2
J
2
,
v
r
v
n2
v
n1
,
m
r
J
2
J
1
,
v
v
n1
D
o
4
a
1
2
a
2
,
a
1
1 v
2
r
11 m
r
2,
a
2
v
2
r
e
f
1
1t 2
f
2
1t 2
f µ
M
1
1v
2
r
2
2
k
t1
D
o
v
2
r
M
1
k
t1
D
o
∂cosvt
X
2
1j2
11.5
2
0.4243 j2F
2
21
4
0.5657 j
3
2.04
2
0.2828 j0.50002
X
1
1j2
10.5 0.1414 j2F
2
21
4
0.5657 j
3
2.04
2
0.2828 j0.50002
x
2
1t 221.2 sin 120t 3.1357 2 3.83 sin 120t 3.10722
mm
x
1
1t 28.8 sin 120t 3.1357 2 9.2 sin 120t 3.10722
mm
Answers to Selected Exercises 699
