Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

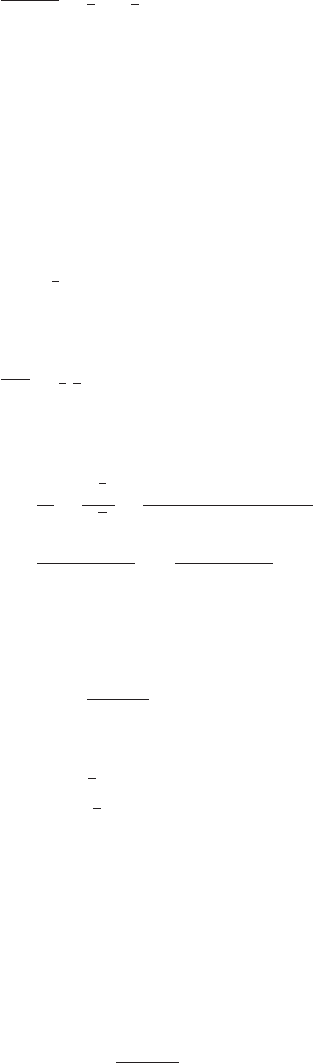
Furthermore, from Eqs. (F.5) and (F.2),
(F.6)
Multiplication
(F.7)
where we have used the identity j
2
1 in arriving at the final expression.
We notice that the special case of multiplying a complex number by it com-
plex conjugate results in
(F.8)
which is a real quantity. Furthermore, from Eqs. (F.2) and (F.7),
(F.9)
Division
(F.10)
provided that z
2
≠ 0.
Absolute Value (Modulus)
(F.11)
Then, from Eqs. (F.11) and (F.2), we see that
(F.12)
Polar Form
The polar coordinates (r, u) corresponding to the complex variable z x jy
can be determined from the equations
(F.13)
where
(F.14)r 0z 0 2x
2
y
2
x r cos u,
y r sin u
0z
1
z
2
0 0z
1
00z
2
0
0z
1
0
2
z
1
z
1
0z
1
0 0z
1
0
0z
1
0 2a
2
1
b
2
1
a
1
a
2
b
1
b
2
a
2
2
b
2
2
j
b
1
a
2
b
2
a
1
a
2
2
b
2
2
z
z
1
z
2
z
1
z
2
z
2
z
2
1a
1
jb
1
21a
2
jb
2
2
1a
2
jb
2
21a
2
jb
2
2
z
1
z
2
z
1
z
2
a
2
1
b
2
1
z z
1
z
1
1a
1
jb
1
21a
1
jb
1
2
1a
1
a
2
b
1
b
2
2 j1b
1
a
2
b
2
a
1
2
a
1
a
2
j1b
1
a
2
b
2
a
1
2 j
2
b
1
b
2
z z
1
z
2
1a
1
jb
1
21a
2
jb
2
2
z
1
z
2
z
1
z
2
680 APPENDIX F Complex Numbers and Variables
is called the magnitude (or amplitude) of z and
(F.15)
is called the argument (or phase) of z. Thus, the polar form of z is
(F.16)
Equation (F.16) can be given a graphical interpretation as shown in Figure F.1.
From Eq. (F.16), we note that
(F.17)
Exponential function
If the complex variable z x jy, then
(F.18)
Comparing Eq. (F.18) with Eq. (F.16), we note that the argument of e
z
is y. If
x 0, then Eq. (F.18) gives
(F.19)
which is known as Euler’s formula.
Equation (F.18) has the following properties:
(a) For all values of q, e
z
0.
(b) 0e
z
0 e
x
, since 0e
jy
0 1 and e
x
0.
(c) A necessary and sufficient condition for
is that z 2kjp, where k is an integer.
e
z
1
Re3z4
e
jy
cos y j sin y
e
z
e
x jy
e
x
e
jy
e
x
1cosy j siny 2
jz
dz
du
r 1sin u j cos u2 r 1j
2
sin u j cos u2
z r 1cos u j sin u2
u tan
1
y
x
Complex Numbers and Variables 681
Im
Re[z] rcos
Re
r
Im[z] rsin
FIGURE F.1
Graphical representation of a complex variable and its polar coordinate representation.
Such plots in the complex plane are also called Argand diagrams.
(d) A necessary and sufficient condition that
is that z
1
z
2
2kjπ, where k is an integer.
Trigonometric and Hyperbolic Functions
Noting from Eq. (F.19) that
(F.20)
we obtain the following relations:
(F.21)
These relations can be extended to any complex number z x jy. Thus,
(F.22)
Furthermore, from Eqs. (F.16) and (F.19), we find that
(F.23)
which is known as De Moivre’s theorem.
r
n
1cos nu j sin nu2
z
n
r
n
1cos u j sin u2
n
r
n
e
jnu
cosh jz cos z
sinh jz j sin z
cosh z cos y cosh x j sin y sinh x
sinh z cos y sinh x j sin y cosh x
cos jy
1
2
1e
y
e
y
2 cosh y
sin jy
1
2 j
1e
y
e
y
2 j sinh y
sin z
1
2j
1e
jz
e
jz
2 sin x cosh y j cos x sinh y
cosz
1
2
1e
jz
e
jz
2 cos x cosh y j sin x sinh y
sin y
1
2j
1e
jy
e
jy
2
cos y
1
2
1e
jy
e
jy
2
e
jy
cos y j sin y
e
jy
cos y j sin y
e
z
1
e
z
2
1or e
z
1
z
2
12
682 APPENDIX F Complex Numbers and Variables

683
APPENDIX G
Natural Frequencies and Mode Shapes
of Bars, Shafts, and Strings
In this Appendix, we shall give the governing equations and boundary condi-
tions for the longitudinal oscillations of uniform bars, the torsional oscilla-
tions of uniform circular shafts, and the transverse oscillations of strings
under constant tension. For each of these systems, we shall provide the fre-
quency equations from which the natural frequency coefficients and corre-
sponding mode shapes for several combinations of boundary conditions can
be obtained.
GENERAL SOLUTION FOR THE VIBRATIONS OF BARS, SHAFTS, AND STRINGS
The equations governing the longitudinal vibrations of a uniform bar, a uni-
form circular shaft, and a string under constant tension are given in Table G.1.
It is seen from these equations that the equations for all three systems are of
the form
(G.1)
where, when a bar is being considered, w u(x,t), c f(x,t), a AE, and
b Ar. When a shaft is being considered, w u(x,t), c t(x,t), a JG and
b Jr and when a string is being considered, w y(x,t), c p(x,t), a T
and b Ar. When the externally applied force is absent; that is, c(x,t) 0,
and the system is undergoing harmonic oscillations of the form w(x,t)
£(x)e
jt
, where v is the frequency of oscillation, Eq. (G.1) becomes
(G.2)
where we have introduced the nondimensional quantities given in Table G.1.
When we are considering a bar, then £
a
(h) £
bar
(h) U(h) and ;
2
a
2
bar
d
2
£
a
1h 2
dh
2
2
a
£
a
1h 2 0
a
0
2
w
0x
2
b
0
2
w
0t
2
c1x,t 2

when we are considering a shaft, then £
a
(h) £
shaft
(h) (h) and
; and when we are considering a string, £
a
(h) £
string
(h) Y(h)
and . In Table G.1, the quantity c
bar
is the speed at which a distur-
bance travels longitudinally within the bar and t
bar
is the time that it takes for a
disturbance to travel the length of the bar. Similar interpretations are valid for
the shaft and the string.
2
a
2
string
2
a
2
shaft
684 APPENDIX G Natural Frequencies and Mode Shapes of Bars, Shafts, and Strings
TABLE G.1
Equations of Motion for Bars, Circular Shafts, and Strings and Definitions of Quantities used in Appendix G.
Longitudinal Motion of a Bar
Torsional Motion of a
Transverse Motion of a String
Circular Shaft
Definitions: Dimensional Quantities
Symbol Description Symbol Description Symbol Description
u(x,t) Axial displacement (m) u(x,t) Rotation (rad) y(x,t) Transverse displacement (m)
x Axial location (m) x Axial location (m) x Location (m)
t Time (s) t Time (s) t Time (s)
A Cross-section area (m
2
) J Polar inertia (m
4
) A Cross-section area (m
2
)
E Young’s modulus (N/m
2
) G Shear modulus (N/m
2
) T Tension (N)
L Length of bar (m) L Length of shaft (m) L Length of string (m)
U(x) Spatial component of (x) Spatial component of Y(x) Spatial component of
u(x,t) U(x)e
jvt
u(x,t) (x)e
jvt
y(x,t) Y(x)e
jvt
M
o
Attached mass (kg) J
o
Attached mass (kg-m
2
) M
o
Attached mass (kg)
k
bar
Attached translational k
shaft
Attached torsion spring k
string
Attached translational spring
spring (N/m) (N/m) (N/m)
m
bar
rAL, Mass of bar (kg) J
shaft
rJL (kg-m
2
) m
string
rAL, Mass of string (kg)
0
u/
0
x Axial strain (m/m)
0
u/
0
x Shear strain (m/m)
0
y/
0
x Slope (rad)
E
0
u/
0
x Axial stress (N/m
2
) Gr
0
u/
0
x Shear stress (N/m
2
) T
0
y/
0
x Transverse tension (N)
r Density (kg/m
3
) r Density (kg/m
3
) r Density (kg/m
3
)
v Frequency (rad/s) v Frequency (rad/s) v Frequency (rad/s)
f(x,t) Applied force (N/m) t(x,t) Applied torque (N-rad) p(x,t) Applied force (N/m)
r Shaft radius (m)
Definitions: Nondimensional Quantities
Symbol Description Symbol Description Symbol Description
h x/L h x/L h x/L
t
bar
L/c
bar
t
shaft
L/c
shaft
t
string
L/c
string
c
bar
c
shaft
c
string
bar
vt
bar
shaft
vt
shaft
string
vt
string
K
bar
(k
bar
L)/(AE) K
shaft
(k
shaft
L)/(GJ) K
string
(k
string
L)/T
g
bar
M
o
/m
bar
g
shaft
J
o
/J
shaft
g
string
M
o
/m
string
2T/1rA22G/r2E/r
T
0
2
y
0x
2
rA
0
2
y
0t
2
p 1x,t2JG
0
2
u
0x
2
Jr
0
2
u
0t
2
t1x,t 2AE
0
2
u
0x
2
Ar
0
2
u
0t
2
f 1x,t 2
The solution to Eq. (G.2) is
(G.3)
The various boundary conditions that are appropriate to these systems are
summarized in Table G.2. We shall consider the case where the system is un-
dergoing harmonic oscillations, is clamped at h 0, and at h 1, is free with
an attached mass that is constrained by a spring. Then, from Table G.2, we
find that the boundary condition at h 0 is
(G.4a)
and that the boundary condition at h 1 is
(G.4b)
where, from Tables G.1 and G.2, we see that for a bar g
a
g
bar
and K
a
K
bar
;
for a shaft g
a
g
shaft
and K
a
K
shaft
; and for a string g
a
g
string
and K
a
K
string
. It should be realized that Eq. (G.4b) can be reduced to the other four
boundary conditions appearing in Table G.2 by considering the limit as g
a
goes to zero or infinity and/or K
a
goes to zero or infinity as the case may be.
Upon substituting Eq. (G.3) into Eqs. (G.4), we obtain the frequency
equation
(G.5)
and the corresponding mode shape as
(G.6)
where
n,a
is the natural frequency coefficient and n 1, 2 . . . , indicates the
nth natural frequency coefficient. From Table G.1, we see that the natural fre-
quency f
n,a
expressed in Hz is given by
(G.7)
In order to obtain the frequency equations for other boundary conditions,
we use the limiting procedure introduced in Section 9.3.3. The results of this
procedure are summarized
1
in Table G.3. In addition, we have given in
Table G.3 some representative numerical values for
n,a
and their correspon-
ding mode shapes. These values can then be used to obtain the values for the
particular system of interest by substituting the appropriate values of t
a
, g
a
,
and K
a
as defined in Table G.1.
f
n,a
n,a
2pt
a
n 1, 2, . . .
£
n,a
1h 2 sin 1
n,a
h2
cot
n,a
g
a
n,a
K
a
n,a
0
d£
a
11 2
dh
1g
a
2
K
a
2£
a
11 2
£
a
10 2 0
£
a
1h 2 Acos 1
a
h2 Bsin 1
a
h2
General Solution for the Vibrations of Bars, Shafts, and Strings 685
1
The special cases agree with those that can be found in the literature. See for example,
R. Blevins, Formulas for Natural Frequency and Modes Shape, Van Nostrand Reinhold, New
York, 1979, pp. 182ff.

TABLE G.2
Boundary Conditions at h 1 for Bars, Shafts, and Strings.
Bars
Clamped
Free
Free with mass
Shafts
Clamped
Free
Free with mass
Strings
Clamped
Free
Free with mass
0Y
0h
1g
string
2
K
string
2YT
0y
0x
M
o
0
2
y
0t
2
k
string
y
TT
Free with mass
and spring
0Y
0h
K
string
YT
0y
0x
k
string
y
TT
Free with
spring
0Y
0h
g
string
2
YT
0y
0x
M
o
0
2
y
0t
2
TT
0Y
0h
0
0y
0x
0
TT
Y 0
y 0
T
Nondimensional Form for
y(h,t) Y(h)e
jwt
Dimensional Form
Boundary
Condition
0®
0h
1g
shaft
2
K
shaft
2®GJ
0u
0x
J
o
0
2
u
0t
2
k
shaft
u
Free with mass
and spring
0®
0h
K
shaft
®GJ
0u
0x
k
shaft
u
Free with
spring
0®
0h
g
shaft
2
®GJ
0u
0x
J
o
0
2
u
0t
2
0®
0h
0
0u
0x
0
® 0
u 0
Nondimensional Form for
u(h,t) (h)e
jwt
Dimensional Form
Boundary
Condition
0U
0h
1g
bar
2
K
bar
2UEA
0u
0x
M
o
0
2
u
0t
2
k
bar
u
Free with mass
and spring
0U
0h
K
bar
UEA
0u
0x
k
bar
u
Free with
spring
0U
0h
g
bar
2
UEA
0u
0x
M
o
0
2
u
0t
2
0U
0h
0
0u
0x
0
U 0
u 0
Nondimensional Form for
u(h, t) U(h)e
jwt
Dimensional Form
Boundary
Condition
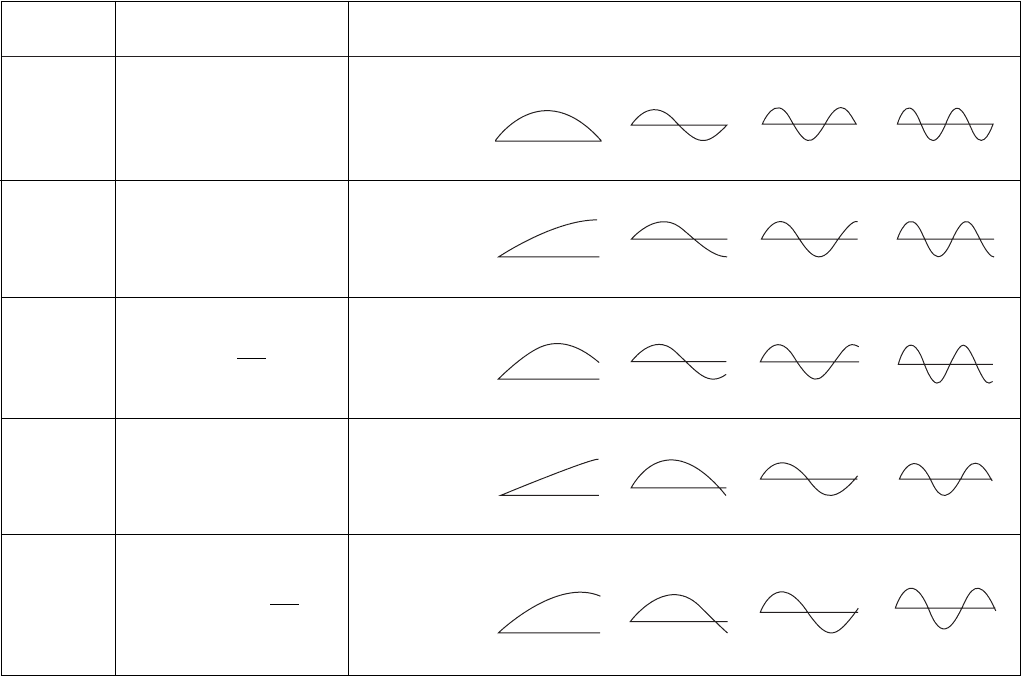
TABLE G.3
Natural Frequency Equations, and Natural Frequency Coefficients and Mode Shapes for Various Combinations of boundary Conditions for the Three Systems
given in Table G.1.
Boundary
Frequency Equation
n 1 n 2 n 3 n 4
Conditions
n,a
/p 123 4
Mode shapes
Node points
†
None 0.5 0.333, 0.667 0.25, 0.5, 0.75
n,a
/p 0.5 1.5 2.5 3.5
Mode shapes
Node points
†
None 0.667 0.4, 0.8 0.286, 0.571, 0.857
n,a
/p 0.8447 1.7362 2.671 3.6315
Mode shapes
Node points
†
None 0.576 0.374, 0.749 0.275, 0.551, 0.826
n,a
/p 3g
a
14 0.2739 1.0904 2.0491 3.0333
Mode shapes
Node points
†
None 0.917 0.488, 0.976 0.330, 0.659, 0.989
n,a
/p 0.64052 1.1373 2.0554 3.0352
and
g
a
14
Mode shapes
Node points
†
None 0.879 0.487, 0.973 0.329, 0.656, 0.988
†
Interior node points only.
cot
n,a
g
a
n,a
K
a
n,a
0
Clamped-
free with
spring and
mass
3K
a
5
cot
n,a
g
a
n,a
0
Clamped-
free with
mass
cot
n,a
K
a
n,a
0
Clamped-
free with
spring
3K
a
5 4
cos
n,a
0
Clamped-
free
sin
n,a
0
Clamped-
clamped
Comparison to a Single Degree-of-Freedom System
The natural frequency of a single degree-of-freedom system composed of a
mass M
o
suspended from a bar whose spring constant is given by Case 1 in
Table 2.3 is
(G.8)
The natural frequency of this same system when it is determined from Eq.
(G.5) when K
bar
0 is
(G.9)
where we have used the definitions appearing in Table G.1. The difference in
their numerical values can be represented by the percentage error e
bar
as
(G.10)
A plot of Eq. (G.10) is given in Figure G.1, where it is seen that for the
error to be less than 5%, g
bar
3.3 and for the error to be less than 2%,
g
bar
8.3.
We now consider the determination of the natural frequency for the tor-
sional oscillations of a single degree-of-freedom system composed of a mass
with polar mass moment of inertia J
o
that is attached to a shaft whose spring
constant is given by Case 3 in Table 2.3. In this case, we have that
(G.11)
The natural frequency of this same system when it is determined from Eq.
(G.5) when K
shaft
0 is
(G.12)
where we have used the definitions appearing in Table G.1. The difference in
their numerical values can be represented by the percentage error e
shaft
as
(G.13)
A plot of Eq. (G.13) is the same as that given in Figure G.1, except that
g
bar
is replaced by g
shaft
.
100 a
1
1,shaft
2g
shaft
1 b
e
shaft
100 a
v
sdof
v
1,shaft
1 b 100 a
L
1,shaft
B
GJ
LJ
o
B
r
G
1 b
v
1,shaft
1,shaft
t
shaft
c
shaft
1,shaft
L
1,shaft
L B
G
r
v
sdof
B
GJ
LJ
o
100 a
1
1,bar
2g
bar
1b
%
e
bar
100 a
v
sdof
v
1,bar
1b 100 a
L
1,bar
B
AE
LM
o
B
r
E
1b
%
v
1,bar
1,bar
t
bar
c
bar
1,bar
L
1,bar
L B
E
r
v
sdof
B
AE
LM
o
688 APPENDIX G Natural Frequencies and Mode Shapes of Bars, Shafts, and Strings
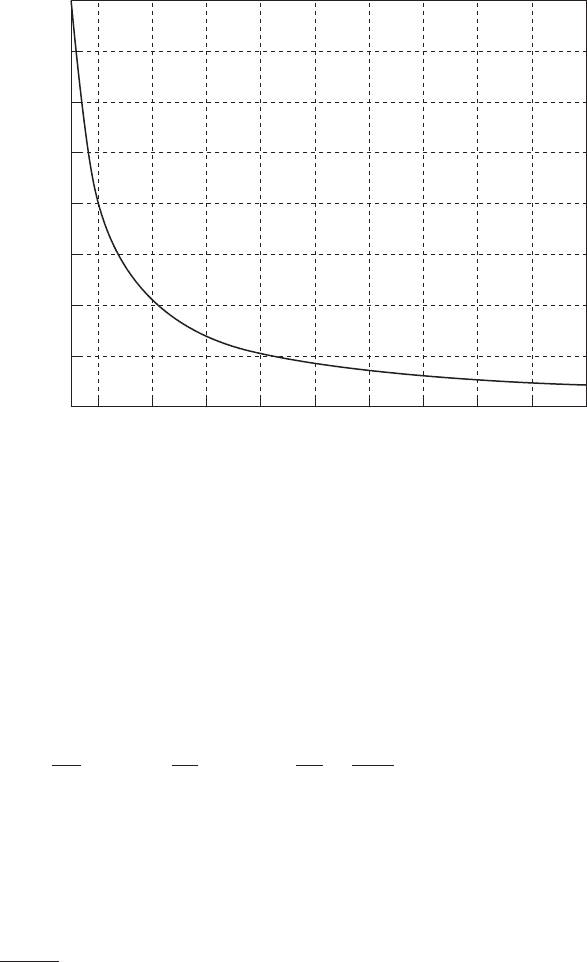
Transverse Vibrations of Strings with In-Span Mass and Spring
The equation governing the transverse vibration of a uniform string of length
L (m) that is stretched with a tension T (N) and is carrying a mass M
o
(kg) at
an interior location L
1
(m) and restrained by a spring k
spring
(N/m) at location
L
2
(m) is
2
(G.14)
where y y(x,t) is the transverse displacement of the string, p(x,t) is the exter-
nally applied force per unit length, A is the area of the string cross section (m
2
)
and r is its density (kg/m
3
). When the externally applied force is absent; that is,
p(x,t) 0, and the shaft is undergoing harmonic oscillations of the form
y(x,t) Y(x)e
jt
, where is the frequency of oscillation, Eq. (G.14) becomes
(G.15)
where h
j
L
j
/L, j 1, 2, and the other quantities are defined in Table G.1.
d
2
Y1h 2
dh
2
2
string
31 g
s
d1h h
1
24Y1h2 K
string
d1h h
2
2Y1h2 0
T
0
2
y
0x
2
crA
M
o
L
d1x L
1
2d
0
2
y
0t
2
k
string
L
d 1x L
2
2y p1x,t 2
General Solution for the Vibrations of Bars, Shafts, and Strings 689
16
14
12
10
8
6
4
2
0
246810
%
12 14 16 18 20
FIGURE G.1
The error between a single degree-of-freedom approximation where a bar (a bar) or shaft
(a shaft) is considered as a massless spring and Eq. (G.5) (with K
a
0) where the mass of
the bar or shaft is included.
2
E. B. Magrab, Vibrations of Elastic Structural Members, Sijthoff & Noordhoff International
Publishing Co., The Netherlands, 1979, pp. 66–72.
