Awrejcewicz J. Numerical Simulations of Physical and Engineering Processes

Подождите немного. Документ загружается.

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems 3

0.01 0.1 1 10 100

1. 10

-6

0.0001

0.01

r/a

(r)/n

(0)

W(0)=2

W(0)=10

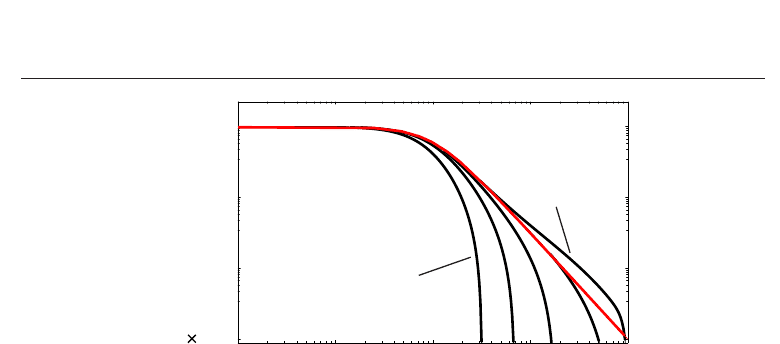
Fig. 1. Black curves denote the number density of the King model n

(r) as a function of the

radius normalized with the core radius, r/a,forseveralW

(0). As the curve changes from left

to right, W

(0) gets larger from 2 to 10 in steps of 2. The red curve means the approximated

formula, 1/

(1 + r

)

3/2

,forlargerW(0).

words the additive noise, can unveil the dynamics toward the steady state described by the

Maxwell-Boltzmann distribution. However, we cannot introduce the randomness into the

system without any evidence. Then, we must conﬁrm that each orbit is random indeed. Of

course, it is impossible to understand orbits of stars in globular clusters from observations.

Thus, we must use numerical simulations.

From the numerical simulations of SGS, the ground that we can use the random noise becomes

clear. The special Langevin equation includes additive and multiplicative noises. By using

this stochastic process, we derive that non-Maxwell-Boltzmann distribution of SGS especially

around the origin. The number density can be obtained through the steady state solution

of the Fokker-Planck equation corresponding to the stochastic process. We exhibit that the

number density becomes equal to the density proﬁles around the origin, Eq. (7), by adjusting

the friction coefﬁcient and the intensity of the multiplicative noise.

Moreover, we also show that our model can be applied in the system which has a heavier

particle (5-10 times as heavy as the surrounding particle). The effect of the heavier particle

in SGS, corresponding to a black hole in a globular cluster, has been studied for long

time. If the black hole is much heavier than other stars, a cusp of the density distribution

appears at the center of a cluster (Peebles, 1972; Bahcall & Wolf, 1976; 1977). The observations

which suggest that intermediate mass black hole (IMBH,

∼ 10

−10



)isintheglobular

cluster in recent years are accomplished one after another (Clark et al., 1975; Newell et al.,

1976; Djorgovski & King, 1984; Gebhardt et al., 2002; Gerssen et al., 2002; Noyola et al., 2008).

Although these studies are very interesting, our model does not treat these situations: in our

model, the heavier particle is too lighter than IMBH. Our model corresponds small globular

cluster (10

stars) with only a stellar black hole ( 1 −10M



Here, note that we have reported similar results in our previous letter (Tashiro & Tatekawa,

2010). In this paper, however, we demonstrate how we executed our numerical simulations.

Moreover, a treatment for stochastic differential equations becomes precise, and so the

analytical result derived by a different method changes a little.

303

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems

4 Will-be-set-by-IN-TECH

This paper is organized as follows. In Sec. 2.1, and Sec. 2.2, we provide brief explanations

about a machine and a method we used when we did numerical simulations, respectively. In

Sec. 2.3, we investigate number densities derived from our numerical simulations where all

particles of SGS with a mass m and a particle with a mass M interact via the gravitational

force. Then, we show the densities are like that of the King model and both the exponent and

the core radius are dependent on M. In Sec. 3.1, forces inﬂuencing each particle of SGS are

modeled. Then, using these forces, Langevin equations are constructed in Sec. 3.2. Section 3.3

makes it clear that the steady state solution of the corresponding Fokker-Planck equation gives

the same result with the King model. In Sec. 4, we discuss our results and make the relation

between King’s procedure and our idea clear. Section 5 gives a summary of this work.

2. Numerical simulations of SGS using GRAPE

2.1 GRAPE

SGSs require quite long time for relaxation. Furthermore, because only attractive force is

exerted on particles in SGS and the gravitational potential is asymptotically ﬂat, we must

compute interaction of all particle pairs. When we treat N particles, the computation

of interaction becomes O

) by direct approach. By these reasons, we require huge

computation for numerical simulation of the evolution of SGS.

For time evolution of SGS, many improvements of algorithm and hardware have been carried

out. First, we consider integrator for simulation. For long-time evolution, both the local

truncation error and the global truncation error are noticed. These error occur deviation of the

conservation physical quantities such as total energy. For compression of the global truncation

error, symplectic integrator has been developed. The symplectic integrator conserves the

total energy for long-time evolution. We apply 6th-order symplectic integrator for the time

evolution of SGS. Secondly, we apply special-purpose processor for the computation of the

interaction. Most of the computation of the time evolution in SGS is 2-body interaction.

As special-purpose processors, GRAPE system has been developed (Sugimoto et al., 1990).

GRAPE system can compute 2-body interaction from position and mass of particles quickly. In

our study, we apply GRAPE-7 chip, which consists of Field-Programmable Gate Array (FPGA)

for computation of the interaction (Kawai & Fukushige, 2006). GRAPE-7 chip implements

GRAPE-5 compatible pipelines

. The performance of GRAPE-7 chip is approximately 100

GFLOPS and is almost equal to a processor of present supercomputers, but the energy

consumption of the chip is only 3 Watts. Using sophisticated integrator and special-purpose

processor, we have analyzed time evolution of SGS.

2.2 Symplectic integrator

For time evolution, we must choose reasonable integrator for simulation. For long-time

evolution, not only the local truncation error but also the global truncation error is noticed.

For example, 4th-order Runge-Kutta method has been applied for time evolution of physical

systems (Press et al., 2007). Although its local truncation error is O



(Δt)



,becauseitserror

accumulates, the global truncation error increases during time evolution. For example, we

GRAPE-5 computes low-accuracy 2-body interaction. If we treat collisional systems, i.e., the

effect of 2-body relaxation cannot be neglected, we should use high-accuracy chip such as

GRAPE-6 (Makino et al., 2003). As we will mention later, because our simulation notices until 100 t

we can simulate the systems with GRAPE-7 chip.

304

Numerical Simulations of Physical and Engineering Processes

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems 5

apply 4th-order Runge-Kutta method for the harmonic oscillation.

.(8)

Using exact solutions, the orbit of the harmonic oscillation in the phase space draws a circle.

Of course, the total energy is conserved. On the other hand, when we apply 4th-order

Runge-Kutta method for time evolution, the total energy is decreased monotonically.

(t)=



−

(

Δt

)

+ O



(

Δt

)







+ q



.(9)

The orbit of the harmonic oscillation in the phase space draws a spiral and it converges

to origin (p

= q = 0). When we consider long-time evolution, 4th-order Runge-Kutta

method is not reasonable integrator. If Hamiltonian of physical system is given, we can apply

symplectic integrator which based on canonical transformation (Ruth, 1983; Feng & Qin,

1987; Suzuki, 1992; Yoshida, 1993). This method suppresses increase of the global truncation

error. In generic case, the symplectic integrator is implicit method. If Hamiltonian is

divided to coordinate parts and momentum parts, the integrator becomes explicit method.

The procedure of low-order integration becomes easy more than Runge-Kutta method. The

simplest integrator is called "leap-ﬂog method" (2nd-order integrator).



Δt



= p(t)+

Δt

(

x(t)

)

, (10)

(t + Δt)=x(t)+Δt · p



t +

Δt



, (11)

(t + Δt)=p



t +

Δt



Δt

(

x(t + Δt)

)

. (12)

Using leap-ﬂog method for the harmonic oscillator, the following equation is satisﬁed.

+ q

Δt

= const. . (13)

Therefore the orbit in the phase space draws an oval. The deviation from the exact solution is

suppressed. To suppress the local truncation error, higher-order symplectic integrators have

been developed. We apply 6th-order symplectic integrator for time evolution of SGS (Yoshida,

1990).

= q

i−1

+ c

Δt

p(q

i−1

)(1 ≤ i ≤ 8) , (14)

= p

j−1

+ d

Δtp

(1 ≤ j ≤ 7) , (15)

where p

= p(t), q

= q(t), p

= p(t + Δt), q

= q(t + Δt). The coefﬁcients c

,andd

are

shown in Tab. 1.

The symplectic integrator conserves the total energy and the symplectic structure in

generic cases. When we use n-th order symplectic integrator, the local truncation error

of the total energy becomes O



(Δt)

n+1



. Furthermore, the global truncation error is not

accumulated (Sanz-Serna, 1988).

305

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems

6 Will-be-set-by-IN-TECH

1 0.39225680523878 0.78451361047756

2 0.510043411918458 0.0235573213359357

−0.471053385409757 −1.17767998417887

4 0.06875316825252 1.31518632068391

5 0.06875316825252

−1.17767998417887

−0.471053385409757 0.0235573213359357

7 0.510043411918458 0.78451361047756

8 0.39225680523878

Table 1. Coefﬁcients of 6th-order symplectic integrator (Solution A in (Yoshida, 1990)).

In SGS, because the interaction at zero distance diverges, the local truncation error

would diverge in long-time evolution. For avoidance of this divergence, some kind of

softening parameter has been introduced to gravitational interaction. When the nature

of the pure gravity is analyzed, the regularization procedure of interaction is required

(Kustaanheimo & Stiefel, 1965; Aarseth, 2003).

2.3 Steady number density in numerical simulation

Now, we investigate the steady number density (SND) of the SGS with a mass m including

a particle with a mass M by numerical simulation. In particular, we show that SNDs have a

core and behave as a power law outside the core.

The system is composed of N

= 10000 particles. At t = 0, all velocities of the particles are

zero and they are distributed by n

(r) ∝ (1 + r

)

−5/2

(0 ≤ r ≤ 4a

), which is the density

in real space of Plummer’s solution (Binney & Tremaine, 1987). In this SGS, we put another

particle with a mass M in the origin at t

= 0. We shall change the mass as M/m = 1, 5, and 10.

Throughout this paper, we adopt a unit system where the core radius of Plummer’s solution

, the initial free fall time t

, and the total mass N · m are unity.

We started the numerical simulation under these conditions. For dynamical evolution, we

used GRAPE-7 at Center for Computational Astrophysics, CfCA, of National Astronomical

Observatory of Japan. For the computation of gravitational force, we applied Plummer’s

softening: the potential energy between the ith and jth particles separated by a distance r

−Gm



+ ε

,whereε

is the softening parameter. We set ε

= 10

−3

. For time evolution,

we used 6th-order symplectic integrator (Yoshida, 1990). The time step for the simulation is

deﬁned as Δt

= 10

−5

. We carried out simulations until t = 100 t

. During simulations, the

error in total energy was less than 0.1%.

First, most particles collapse into the origin within several t

. After approximately 20 t

,the

distribution becomes stable and the system reaches the steady state. Of course, we can conﬁrm

whether the system becomes steady or not from the proﬁle of the number density. However,

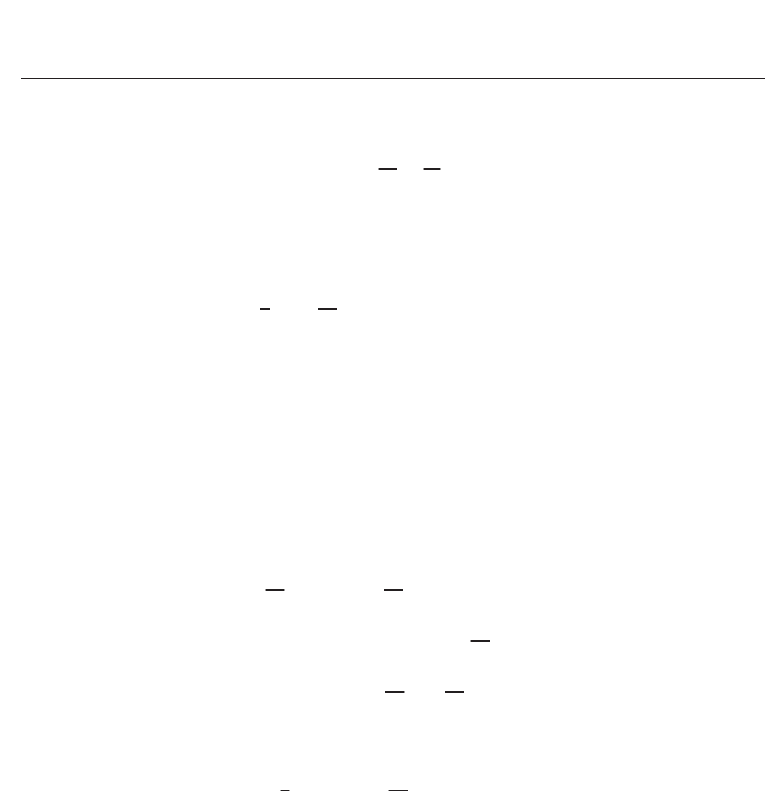
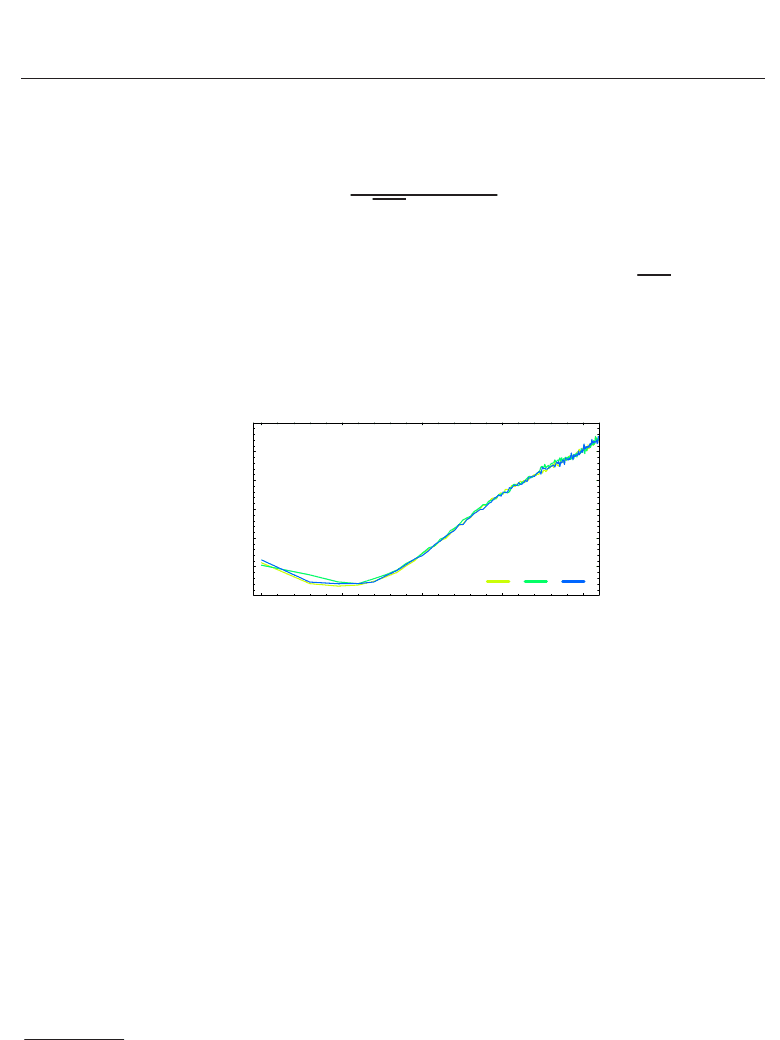
furthermore we also focus on the number of particles inside a sphere. Figure 2 shows the

change of the number inside the sphere with a radius 1 in time. During the collapse, the

number becomes large. After that, the number decreases, which means that many particles

306

Numerical Simulations of Physical and Engineering Processes

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems 7

with positive energy evaporated from inside of the sphere, and so the number becomes about

6000 on average. For other radii, similar changes of the number in time can be seen.

0 20 40 60 80 100

5000

5500

6000

6500

7000

number of particles

1m 5m 10m

Fig. 2. Change of the number of particles inside a sphere with a radius 1 in time for

M/m

= 1, 5, and 10.

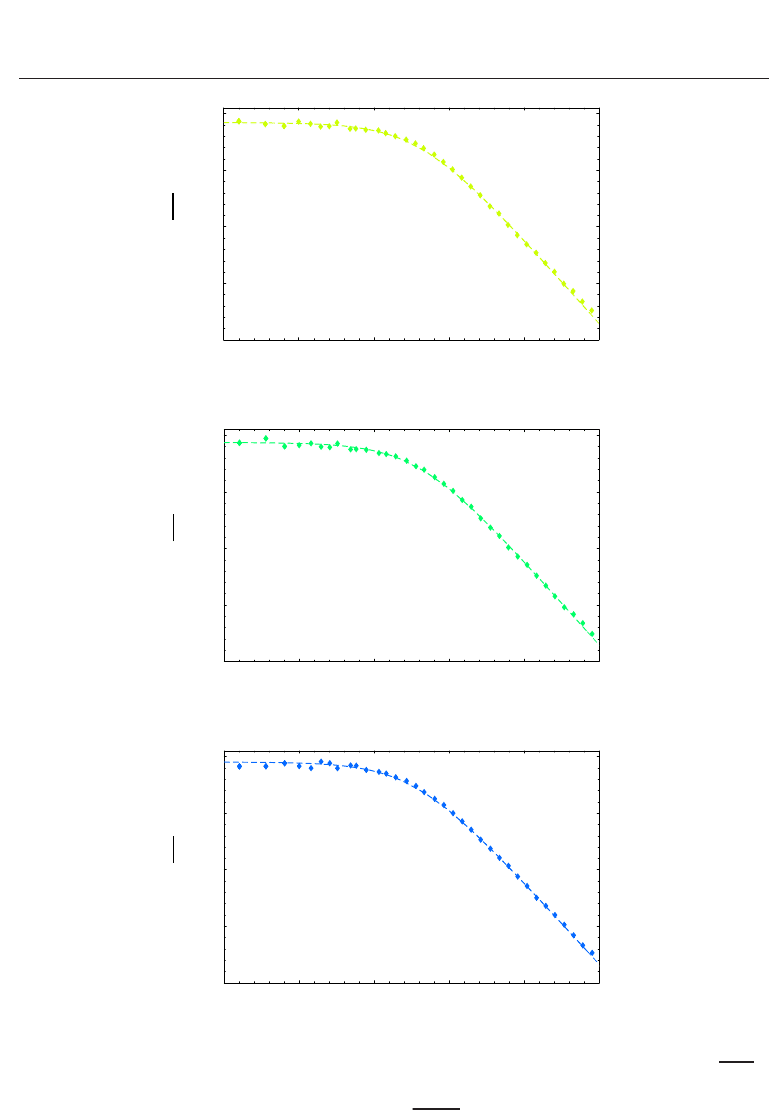
SND is calculated by taking the time average during the steady state. In Fig. 3, we show the

logarithm of SND as a function of log r for M/m

= 1, 5, and 10. For each M,theSNDhasa

core and behaves as a power law at r larger than the core radius. Here, we ﬁt SNDs around

the core by

ﬁt

(r)=C/(1 + r

)

. The results are summarized in Tab. 2. For M/m = 1

and 5, κ

 3/2, which is similar to the exponent of the King model. The density at the origin

C increases as M increases, which is simply understood to be a result of many particles being

attracted by the heavier particle.

M/ma× 10

κ C × 10

−5

16.20±0.22 1.46 ±0.03 7.06 ±0.14

56.06

±0.18 1.46 ±0.02 7.57 ±0.13

10 5.68

±0.14 1.43 ±0.02 8.13 ±0.12

Table 2. Best-ﬁt parameters of the function C/(1 + r

)

for steady number densities

shown in Fig. 3

3. Simple model

3.1 Forces acting on each particle of SGS

As shown in the last section, SND is the King-like proﬁle even though the system includes

the heavier particle. In this section, in order to explain these results and derive this

non-Maxwell-Boltzmann distribution around the origin, we demonstrate a simple model

based on stochastic process, which is quite different from the King model.

The reason why stochastic process appears in the SGS is as follows. After the collapse, the

density around the origin becomes high. Thus, the particles around the region disturb the

307

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems

8 Will-be-set-by-IN-TECH

-2 -1.5 -1 -0.5 0

log r

logn(r)

M=1m

(a)

-2.5

-2 -1.5 -1 -0.5 0

log r

logn(r)

M=5m

(b)

-2.5

-2 -1.5 -1 -0.5 0

-2.5

log r

logn(r)

M = 10m

(c)

Fig. 3. Logarithm of the steady number density derived from our numerical simulation, n(r),

as a function of log r for (a) M/m

= 1, (b) M/m = 5, and (c) M/m = 10. In each ﬁgure, the

dashed curve and symbols denote a ﬁtting curve

ﬁt

(r)=C/(1 + r

)

and the result of

our numerical simulation, respectively.

308

Numerical Simulations of Physical and Engineering Processes

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems 9

orbits of other particles repeatedly, so that their movements become random

.Asthetime

at which this disturbance occurs, we introduce the local 2-body relaxation time t

rel

(Spitzer,

1987):

rel

(r)=

0.065σ(r)

n(r)m

ln(1/ε

)

, (16)

where σ

(r) is the standard deviation of the velocity at r;weadoptedln(1/ε

) as the Coulomb

logarithm.

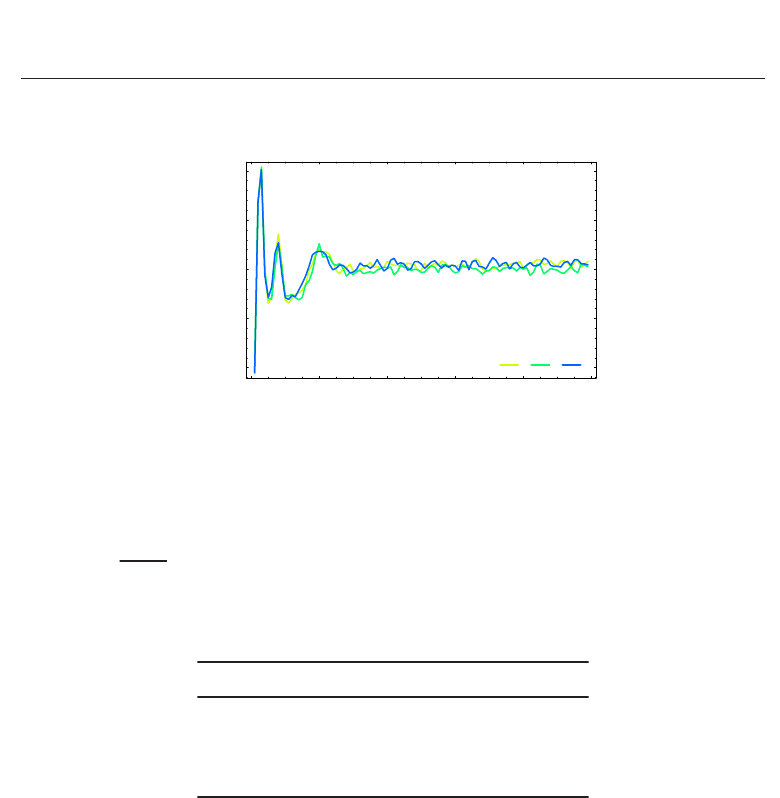
Figure 4 shows the logarithm of t

rel

, which is calculated using the σ(r) and n(r) during the

steady state obtained from our numerical simulation, as a function of log r.Asexpected,t

rel

around the origin is short. Our simulation continues after the collapse at about 80 t

,which

is sufﬁciently longer than the t

rel

around the core. As radius increases, however, t

rel

becomes

longer than the rest of our simulation time, which means that no stochastic motion occurs at

alarger. Therefore, note that our model is valid only in the neighborhood of the core.

-2 -1.5 -1 -0.5 0

logr

1.0

1.5

2.0

2.5

3.0

logt

rel

1m 5m 10m

Fig. 4. Logarithm of the local 2-body relaxation time t

rel

as a function of log r for M/m = 1, 5,

and 10.

When constructing our model, the following points are premised: the model describes the

stochastic dynamics near the steady state and the mean distribution is spherically symmetric.

As is well known, the gravitational force at r arising from such a spherically symmetric system

depends only on the particles existing inside a sphere with a radius r, and this attractive force

acts along the radial direction. In other words, this mean force

−F(r) is the gradient of the

mean potential:

−F(r)=−m∂Φ(r)/∂r (< 0). Indeed, lim

r→0

F(r)=0. Hence, F( r) can be

expanded around the origin as

(r)=c

r + O( r

) . (17)

It will be clariﬁed later that the lowest exponent must be 1 and the coefﬁcient c

is related to

the number density at the origin C as

= 4πGm

C/3 . (18)

Generally, a particle going into a region where the gravitational potential is deep, e.g. the core of SGS,

attains a high velocity. Because of many disturbances around the core, however, the mean velocity

of the particle decreases, which is, naively speaking, the dynamical friction (Binney & Tremaine, 1987).

Therefore, even though the heavier particle at the origin of the system makes the gravitational potential

deeper, there are few particles that can escape from the core smoothly. Then more particles are drawn

toward the heavier particle.

309

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems

10 Will-be-set-by-IN-TECH

For M/m = 1, we can identify another particle together with the other particles. Contrary

to this, we must consider the effect of the particle in the case M/m

= 1. Now, we suppose

that the heavier particle exists at the origin. Then, the attractive force by this particle at r is

−F (r)=−GmM/r

. We can estimate F(r) around this region as F(r) ∼ c

r = 4πGm

Cr/3,

whereweusedEq.(18). Thus,F

(r)/F(r) ∼ 3Mr

−3

/4πCm. This ratio becomes signiﬁcant

when r

 10

−2

,sinceC ∼ 10

asshowninTab.2. Therefore,ifr is smaller than the radius,

particles are inﬂuenced by not only F

(r) but also F (r), so that the core disappears. In fact, we

have performed a numerical simulation with the heavier particle ﬁxed at the origin, where this

result is conﬁrmed. On the other hand, Miocchi improved the King model in order to describe

the steady state of a globular cluster including an IMBH and reported that the density becomes

cuspy as the mass of the black hole increases (Miocchi, 2007). The nature of a globular cluster

when a massive black hole is much heavier than the surrounding star, have been studied as

mentioned in Introduction. In this case, the massive black hole stays at the center mostly.

Then, a cusp of the density distribution at the center appears. Because the heavier particles

in our numerical simulation are not very heavy, the particles are not trapped at the origin.

Therefore, we do not consider the effect of heavier particles explicitly and we suppose that the

particles inﬂuence SGS through the density at the origin C:asM becomes larger, it attracts

more particles and C increases, as shown in Tab. 2. Thus, c

is an increasing function of M.

It is natural to consider that the distribution ﬂuctuates around the mean because of the many

disturbances. In fact, as shown in Fig. 2, the number of particles existing inside the sphere with

a radius 1 ﬂuctuates around the mean value. The ﬂuctuating part of the distribution should

not be spherically symmetric, so that this produces forces along not only the radial direction,

but also other directions. We assume that they are random forces and set their intensity at r

(r). In addition to such random forces resulting from the ﬂuctuating distribution, a particle

at r is expected to be inﬂuenced by random forces generated from neighboring particles. We

set the intensity 2D, which is independent of position.

3.2 Langevin equations

Stochastic dynamics under the above assumptions is described by the following Langevin

equations in spherical coordinates: the radial direction

+ mγ

r = −F(r)+



2H(r)η

(t)+

√

2Dξ

(t) , (19)

the elevation direction

+ mγr

θ =



2H(r)η

(t)+

√

2Dξ

(t) , (20)

and the azimuth direction

+ mγr sin θ

φ =



2H(r)η

(t)+

√

2Dξ

(t) , (21)

where a

, a

,anda

are accelerations along those directions; γ is the coefﬁcient of

dynamical friction in the low velocity limit, independent of velocity (Binney & Tremaine,

1987). In the Chandrasekhar dynamical friction formula, the coefﬁcient is more

complicated (Binney & Tremaine, 1987; Chandrasekhar, 1943). However, we use the

coefﬁcient in such a limit, because the density around the core is so high that particles around

there move slowly.

310

Numerical Simulations of Physical and Engineering Processes

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems 11

Now, we focus on the overdamped limit of these equations, because we have interests in

the stochastic dynamics near the steady state. In the case of the normal Langevin equation

with a constant-intensity noise, we only neglect the inertial term. But, as for special Langevin

equations with noises whose intensity depends on a position, the new force

−∇H(r)/2mγ

should be considered additionally

. Thus, the Langevin equations in the overdamped limit

becomes as follows:

radial direction : mγ

= −F(r)+



2H(r)η

(t)+

√

2Dξ

(t) −

2mγ



(r) , (22)

elevation direction : mγr



2H(r)η

(t)+

√

2Dξ

(t) , (23)

azimuth direction : mγr sin θ



2H(r)η

(t)+

√

2Dξ

(t) , (24)

where the prime indicates a derivative with respect to r. The noises in each Langevin equation,

(t) and η

(t)(i, j = r, θ,and φ), are zero-mean white Gaussian and correlate only with

themselves. Indeed, the correlation function is the Dirac delta function

Here, revisit the position-dependent intensity noise. We have introduced such a noise in order

to represent a random force originating from the ﬂuctuation of the distribution around the

mean value which yields the mean force

−F(r). Thus, the ﬁrst and the second terms on the

right-hand side of Eq. (22) must denote that the mean force acting along radial direction is

ﬂuctuating. As a minimal formulation describing this situation, we propose the following

one:

− F(r){1 −

√

2η

(t)} , (25)

in which  is a positive constant. This can be realized by setting

(r)=F(r)

. (26)

Note that this ﬂuctuating mean force is the essential feature for SGS. Since the gravitational

force is a long-range one, each particle is inﬂuenced from the whole system. The mean force

is produced by the mean potential which is decided by the number density in the steady state

through the Poisson equation. Obviously, this number density determines only the mean

positions of the particles, and they do not remain stationary at those positions: they ﬂuctuate.

Then, the mean force also ﬂuctuates.  indicates the extent of ﬂuctuations. If  is 0, that is,

means the mean force does not ﬂuctuate, the stochastic dynamics of each particle is governed

only by the constant-intensity random force originating from the neighboring particles. Then,

the Maxwell-Boltzmann distribution is obtained as the steady solution, by which the number

density of globular clusters cannot be explained as written in Introduction.

This force is necessary in order to interpret products in theses Langevin equations as Storatonovich

ones in the corresponding stochastic differential equations. See details in Ref. (Sekimoto, 1999).

It may not be natural that correlations of the random forces generated from the gravity are described

by the Dirac delta function. But in this paper, for simplicity, the correlation times are assumed to be

negligible. In other words, the time resolution of our simple model in the over-damped limit is assumed

to be much longer than the correlation times.

311

Stochastic Dynamics Toward the Steady State of Self-Gravitating Systems

12 Will-be-set-by-IN-TECH

3.3 Fokker-Planck equation and the asymptotic steady solution around the origin

From the Langevin equations (22), (23), and (24), we obtain the Fokker-Planck equation

governing the spherically symmetric probability distribution function (PDF) P

(r, t)

∂

∂t

(r, t)=

(mγ)



∂

∂r

∂

∂r



(r, t)+

mγ

∂

∂r

F(r)P(r, t)



(mγ)



∂

∂r

F(r)

∂

∂r

(r)



(r, t) ,

in which we have replaced H

(r) by F(r) using Eq. (26). Then, the PDF with the Jacobian

(r, t) ≡ 4πr

P(r, t) satisﬁes the following Fokker-Planck equation.

∂

∂t

(r, t)=

(mγ)



∂

∂r

−

∂

∂r



(r, t)+

mγ

∂

∂r

(r)ρ(r, t)



(mγ)



∂

∂r

−

∂

∂r



(r)

ρ(r, t) (27)

This equation is useful when integrating with respect to r.

The steady state solution ρ

(r) satisﬁes Eq. (27) with the left-hand side zero. By integrating

the equation with respect to r,wehave



(mγ)



(mγ)

F(r)





(r)

−



(mγ)

−



(mγ)



(r)F



(r) −

(r)



−

F(r)

mγ



(r)=const. . (28)

Now, we impose the binary condition that P

(r) ≡ ρ

(r)/(4πr

) and the derivative do not

diverge at the origin. Then, when r

→ 0,

(r)=O(r

) , (29)

and

lim

r→0



(r)=lim

r→0

4π(2rP

(r)+r



(r)) = 0 , (30)

by which the constant on the right-hand side of Eq. (28) is decided and we obtain



+ F( r)





(r)=−



(r)



2F



(r)+mγ



−2



D + F(r)



(r) . (31)

Thus, if F

(r) is obtained, ρ

(r) can also be obtained. Here, F(r) relates with SND, n

(r),

through the following relation, since

−F(r)=−mΦ



(r).



(r)+

(r)=4πGm

(r) (32)

Incidentally, the SND can be obtained by multiplying PDF in the steady state by total number

(r)=NP

(r)=

Nρ

(r)

4πr

. (33)

312

Numerical Simulations of Physical and Engineering Processes