ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

Traditionally, flat plate impact tests have been used to obtain high strain rate yield data, shock wave response

data, and equation of state data for materials undergoing uniaxial strain. Uniaxial strain refers to a three-

dimensional state of stress in which deformation or strain occurs in only one direction—the direction of

loading. The uniaxial strain condition persists for only a short period of time until stress waves originating at

lateral boundaries reach the specimen interior. In a typical experiment, this time period is on the order of

several to tens of microseconds. Uniaxial strain is defined mathematically as:

≠ 0, u

= u

= 0

(Eq 19)

where x is the direction of loading, u

is the displacement in that direction, and y and z are orthogonal directions

in a plane normal to x. The strains are obtained from the displacement derivatives, thus:

≠ 0, ε

= ε

= 0

(Eq 20)

The flat plate impact test is performed by launching a flat flyer plate against a second stationary target plate.

Compressed gas guns, propellant guns, magnetic accelerators, and explosives have all been used to launch the

flyer plate (Ref 40). Extreme precision must be achieved to eliminate relative tilt at the instant of impact. A

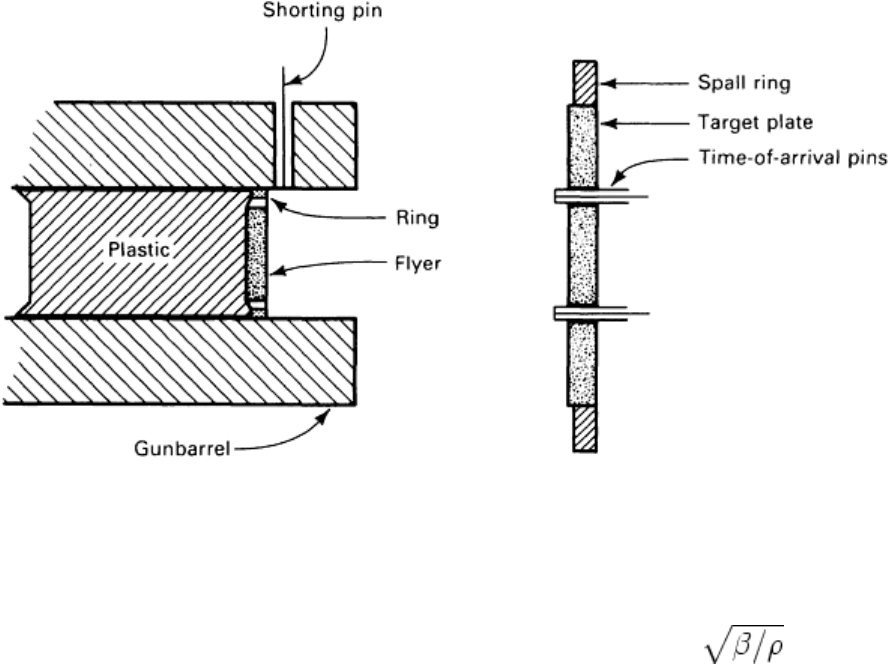
typical experimental setup using a gas gun is shown in Fig. 8. The flyer plate is carried in the gas gun in a

plastic sabot. Velocity of the flyer is determined from the transit time between the shorting pin in the gun barrel

and time-of-arrival pins in the target. The target is supported by a spall ring that suppresses late-time radial

tensile waves.

Fig. 8 Schematic of gas-gun-launched flyer plate impact test setup

The stress waves along the axis normal to the impact plane are shown in Fig. 9. A flyer plate of thickness d,

moving left to right, strikes an initially stationary target of thickness T; the impact occurs at the origin, O, of the

(x, t) coordinates. Elastic-plastic behavior is assumed in Fig. 9. Elastic waves propagate at approximately c

the longitudinal elastic sound speed. Plastic waves propagate at approximately where B is the bulk

modulus. The arrivals of the elastic and plastic waves at the target rear surface are denoted as E and P.

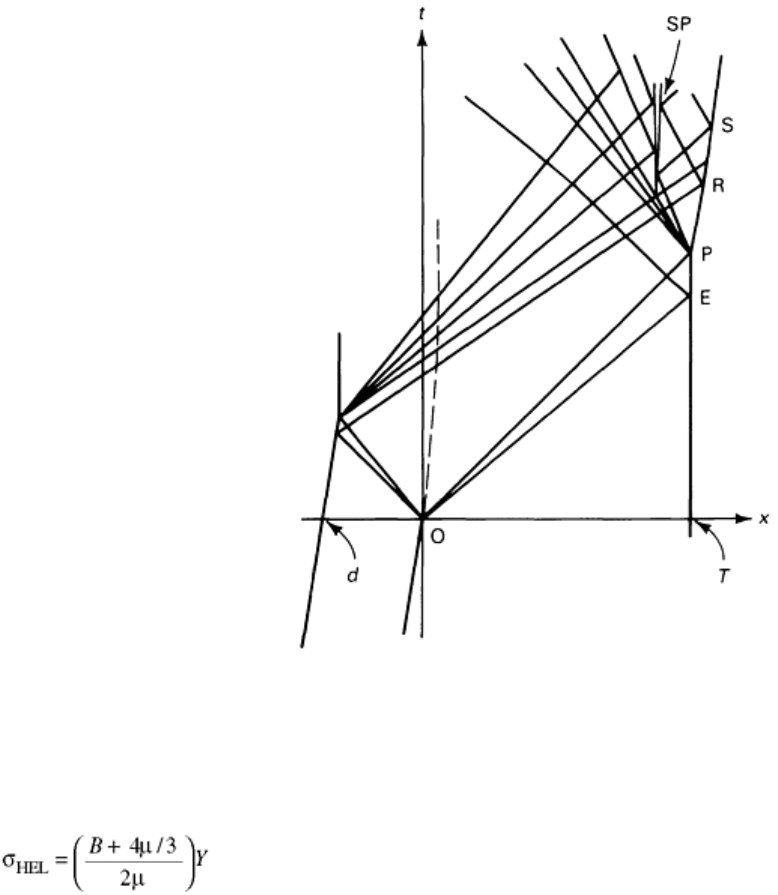
Fig. 9 Lagrangian diagram showing stress waves in flyer plate experiment

Propagation speeds are always relative to the material into which the wave is moving. Strain occurs only at the

wave fronts. The amplitude of the E wave in Fig. 9 is known as the Hugoniot elastic limit (HEL) and is simply

related to the uniaxial yield stress, Y, as:

(Eq 21)

where μ is the shear modulus. The final state of the shocked material is characterized by a stress and particle

velocity. The functional relationship between these two variables depends on the material and is known as the

Hugoniot. The state behind the P wave in Fig. 9 lies on the Hugoniot (see Ref 41 for a discussion of

Hugoniots). If the flyer and target plates are composed of the same material, the particle velocity behind the P

wave is one half the impact velocity.

Reference 42 discusses determination of particle velocity when the flyer and target are composed of different

materials. If the Hugoniot of the target is known, then the stress can be calculated from the particle velocity.

Hugoniots for most engineering metals can be found in Ref 43.

Compressive waves reflect from a free surface as tensile (rarefaction) waves, which begin to arrive at the target

rear surface at point R in Fig. 9. The tensile (rarefaction) waves may interact and cause spall failure. This

causes material separation in the target, which is indicated at point SP in Fig. 9. The sudden relaxation of tensile

stress generates a shock wave that arrives at the free surface at point S.

Spall is a form of tensile failure under an extremely high strain rate and a nearly spherical stress tensor. Spall

usually is characterized by the spall stress, σ

spall

, defined as the highest tensile stress that exists in the material

prior to rupture. When designing spall experiments, the flyer plate diameter, a, must be large enough so that the

phenomena of interest occur within a time a/2c

after the impact.

Flat plate impact tests normally are used to measure σ

HEL

and spall strength. For example, consider the

characterization of a steel by this technique. The value of σ

HEL

for steel is usually between 5 and 15 kilobar

(kbar), a useful unit for analyzing shock experiments (1 kbar = 0.1 GPa). When density is expressed as g/cm

10 and velocity is given in km/s (or, equivalently, mm/μs), stress is given in kbar.

To measure the Hugoniot elastic limit, the impact velocity must be sufficient for the peak stress to exceed σ

HEL

Peak stress is given by:

σ = ρUv

(Eq 22)

where U is shock propagation speed and v is particle velocity. Peak particle velocity is half the impact velocity,

, for a symmetric impact. For steel-on-steel impacts, Eq 22 becomes approximately σ = 200 v

. For σ > σ

HEL

15 kbar, a v

greater than 75 m/s (245 ft/s) is required. This presents no problem when a gas gun is used.

Experiments with v

< 100 m/s (330 ft/s) are often difficult because of impact tilt, which becomes more critical

at low velocities. Also, impact velocity must not be so high that the velocity of the P wave (Fig. 9) exceeds c

That limit for steels usually is greater than 1 km/s (0.6 mile/s). The limit for other materials can be found by

consulting the tables in Ref 43.

Given an appropriate impact velocity, to determine σ

HEL

one of the following measurements must be made. The

peak particle velocity behind the E wave can be measured. This can be accomplished at the free surface with

capacitor gages, sloping mirrors, or a velocity interferometer. The velocity behind the wave is half the free

surface velocity. The stress is related to the free surface velocity by Eq 22 with v = c

Direct measurement of σ

HEL

can be obtained by embedded piezoresistive gages. Manganin and carbon gages

frequently are used for this purpose. This technique requires sectioning the target or using a backing plate and

correcting for partial transmission of the wave transmitted through the interface. Magnetic particle velocity

gages can be used for nonconducting targets, such as plastics and rocks, but they are not suitable for metals.

Spall stress can be determined by two methods. The simplest, in terms of analysis, interpretation, and

experimental technique, is to vary systematically the flyer plate thickness, d, and impact velocity, v

, to

determine the critical values at which rupture occurs. As the flyer plate thickness is increased, the duration of

the compressive and tensile load increases; the load duration is approximately 2d/c

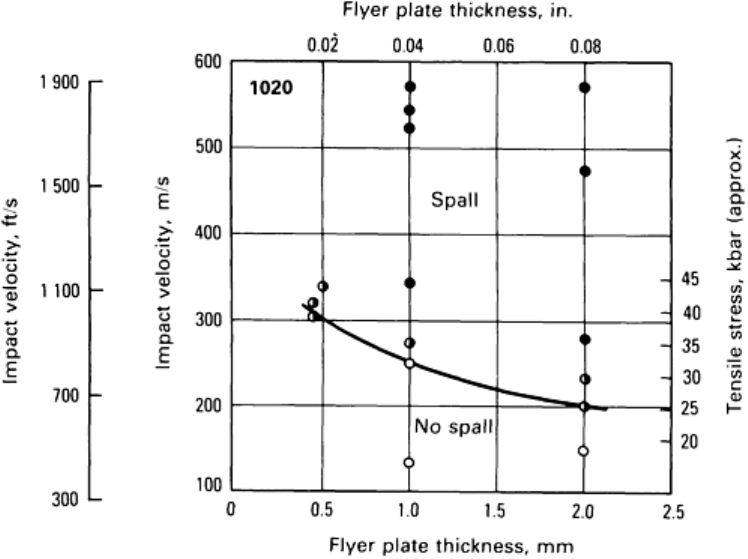
Eventually, for flyer plate thicknesses exceeding about 5 mm (0.2 in.), the spall stress reaches a load duration

limit. In many metals, the limiting spall strength is several times the value of σ

HEL

. Figure 10 illustrates typical

spall stress data for low-carbon steel. The data illustrate that for pulse durations longer than a few

microseconds, the greatest tensile stress that the material can sustain without rupture is 25 kbar.

Fig. 10 Spall data for low-carbon 1020 steel

Interpretation of experiments using thinner flyer plates is more complex because a computer code must be used

to calculate the stress history on the spall plane. Finite difference codes (Ref 41) or method of characteristics

codes (Ref 44) can be used. Finite difference codes are more accurate and more widely applicable than method

of characteristics codes, but the user must be specially trained in this subject.

Another approach to spall characterization is to initiate impact above the spall threshold and to deduce the

material behavior from the free surface velocity, Δv

, data. Figure 11 illustrates a typical free surface velocity

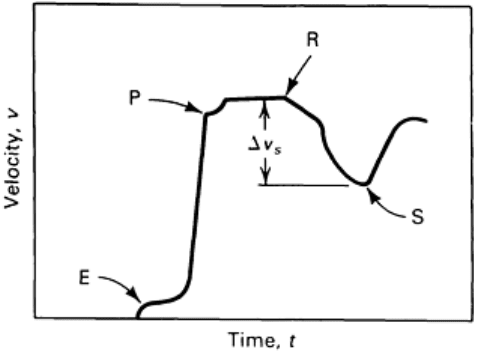
history with spalling. E, P, R, and S refer to the same arrivals as explained in text for Fig. 9. The spall stress is

given approximately by ρc

Δv

/2. However, a more exact determination requires code analysis.

Fig. 11 Free surface velocity data when spall occurs

Split-Hopkinson Bar in Tension

The principles of the split-Hopkinson bar in tension are similar to those in compression, as discussed in the

article “Classic Split-Hopkinson Pressure Bar Testing” in this Volume. The primary differences are the

methods of generating a tensile loading pulse, specimen geometry, and the method of attaching the specimen to

the two bars (incident and transmitter).

Basically, three types of tension split-Hopkinson bars have been developed. The first (Ref 45) involves the use

of compressive pulses in the input and transmitter bars, as in the compressive test. The input bar is solid, while

the transmitter or output bar is a hollow tube of the same cross-sectional area as the input bar. The specimen is a

complex “top-hat” type of geometry, as shown in Fig. 12. The specimen actually is comprised of four parallel

tensile bars of equal cross-sectional area. Although specimen machining is somewhat complex, the test is

conducted in the same manner as compressive testing.

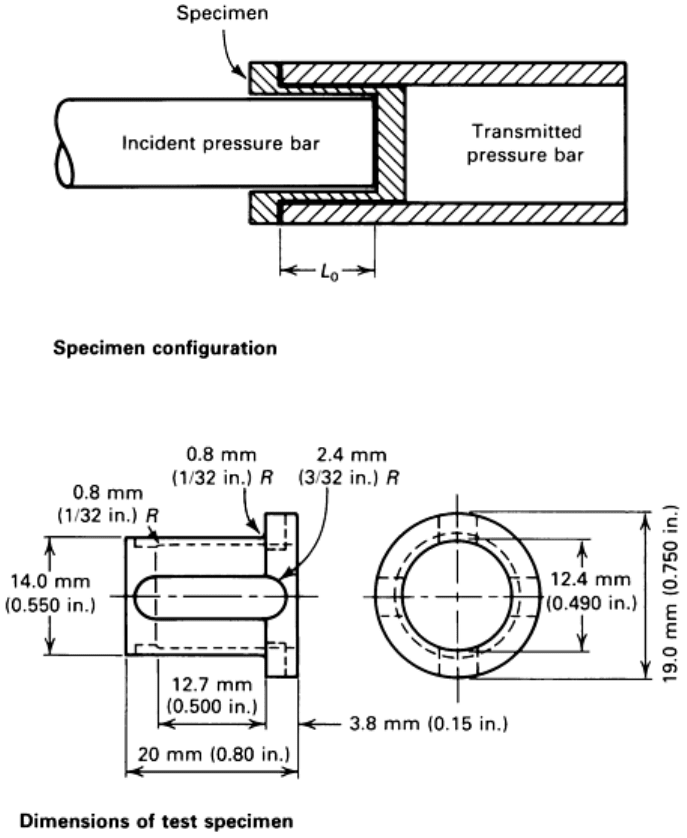
Fig. 12 Details of the split-Hopkinson tension specimen. Source: Ref 45

The second type of tension split-Hopkinson bar test involves the use of a smaller standard type of threaded

tension specimen and generation of a tensile pulse directly on the end of the loading or input bar (Ref 46, 47).

This can be accomplished in several ways, as shown in Fig. 13. In Fig. 13(a), a mass is impacted directly on an

anvil attached to the end of the input bar. In Fig. 13(b), an anvil is loaded by a compressive wave transmitted

through another loading bar that is a hollow tube. The compressive pulse in the loading tube is generated by the

same techniques as the compression split-Hopkinson bar. In Fig. 13(c), a pulse is generated by the detonation of

an explosive against the anvil. In Fig. 13(a) and (c), it is difficult to generate a pulse of constant amplitude,

while in Fig. 13(b) a long time duration is accomplished in the same manner as in compressive testing.

Fig. 13 Schematic of three types of split-Hopkinson tension-loading techniques

The third type of tension test also uses a threaded specimen but uses the reflection of a compression pulse at a

free end and a collar to protect the specimen from initial precompression (Ref 48). Figure 14(a) illustrates an

experimental setup. Figure 14(b) is a Lagrangian x-t diagram, which illustrates the details of wave propagation

in the bars and the experimental procedures. When the striker bar is accelerated against bar No. 1, the impact

generates a compression pulse, the amplitude of which depends on the striker velocity and the length of which

is twice the elastic wave transit time in the striker bar. The pulse travels down the bar until it reaches the

specimen. The threaded tensile specimen is attached to the two pressure bars, as shown in detail “A” of Fig.

14(a).

Fig. 14 Split-Hopkinson bar test using threaded tension specimen. (a) Schematic of tensile loading

apparatus. Source: Ref 48. (b) Lagrangian diagram for tensile loading apparatus. CRO, cathode ray

oscilloscope

After the specimen has been screwed into the bars, a split shoulder or collar is placed over the specimen, and it

is screwed in until the pressure bars fit tightly against the shoulder. The shoulder is made of the same material

as the pressure bars, has the same outer diameter, and has an inner diameter that just clears the specimen. The

ratio of the cross-sectional area of the shoulder to that of the pressure bars is typically 3:4, while the ratio of the

area of the shoulder to the net cross-sectional area of the specimen is typically 12:1.

The compression pulse travels through the composite cross section of the shoulder and specimen in an

essentially undispersed manner. Tightening of the specimen by twisting the pressure bars, the relatively loose

fit of the threaded joint of the specimen into the bars, and the large area ratio of the shoulder to the specimen

ensure that no compression beyond the elastic limit is transmitted to the specimen.

Ideally, the entire compression pulse passes through the supporting shoulder as if the specimen were not

present, although in practice it is difficult to prevent prestraining of the specimen. The compression pulse

continues to propagate until it reaches the free end of bar No. 2. There it reflects and propagates back as a

tensile pulse, ε

, and passes gage No. 2. Upon reaching the specimen at point A as shown in Fig. 14(b), the

tensile pulse is partially transmitted through the specimen, ε

, and partially reflected back into bar No. 2, ε

Note that the shoulder, which carried the entire compressive pulse around the specimen, is unable to support

any tensile loads because it is not fastened to the bars.

Tight fitting of the shoulder against the bars is critical in transmitting the compression pulse down the bars

without significant wave dispersion. Similarly, the tight fit of the threaded tensile specimen against the bars is

essential to achieve smooth and rapid loading of the specimen as the tensile pulse arrives. Failure to remove all

“play” from the threaded joint results in uneven loading of the specimen and spurious wave reflections.

Analysis of the tensile split-Hopkinson bar test is almost identical to that of the compression test. The major

difference is the actual or effective gage length of the specimen. Contrary to the compression test, in which a

right circular cylinder is used, the tensile test uses a cylindrical specimen with an attached shoulder and

additional gripping, such as threads. Because the split-Hopkinson bar test can only provide data on the relative

displacement between the ends of the incident and transmitter bars, an effective gage length generally must be

used. This is equivalent to determining strain in a tensile test through crosshead displacement measurement.

The use of strain gages on test samples to determine an effective gage length is strongly recommended. This

calibration is accomplished easily at low strain rates, preferably in a conventional test machine in which the

crosshead displacement is monitored separately.

As with any uniaxial tensile test, once localized necking occurs, it is no longer possible to simply convert load-

displacement data to stress-strain data. The range of application of the Hopkinson bar test can be extended by

high-speed photography of necking specimens. An analysis that allows estimation of effective stress and strain

from the profile of the necking specimen is described in Ref 49. Photographs can be made with a suitable high-

speed camera system through windows provided in the collar. The major technical difficulty is the precise

synchronization of the exposures with the Hopkinson bar record (Ref 50).

References cited in this section

32. T. Nicholas and S.J Bless, High Strain Rate Tension Testing, Mechanical Testing, Vol 8, ASM

Handbook, ASM International, 1985, p 208–214

33. F.I. Niordson, A Unit for Testing Materials at High Strain Rates, Exp. Mech., Vol 5, 1965, p 29–32

34. C.R. Hoggatt and R.F. Recht, Stress-Strain Data Obtained at High Strain Rates Using an Expanding

Ring, Exp. Mech., Vol 9, 1969, p 441–448

35. D.E. Grady and D.A. Benson, Fragmentation of Metal Rings by Electromagnetic Loading, Exp. Mech.,

Vol 28, 1983, p 393–400

36. A.M. Rajendran and I.M. Fyfe, Inertia Effects on the Ductile Failure of Thin Rings, J. Appl. Mech.

(Trans. ASME), Vol 104, 1982, p 31–36

37. L.M. Barker and R.E. Hollenback, Laser Interferometer for Measuring High Velocities of Any

Reflecting Surface, J. Appl. Phys., Vol 43, 1972, p 4669–4674

38. R.H. Warnes, T.A. Duffey, R.R. Karpp, and A.E. Carden, An Improved Technique for Determining

Dynamic Material Properties Using the Expanding Ring, Shock Waves and High-Strain-Rate

Phenomena in Metals, M.A. Meyers and L.E. Murr, Ed., Plenum Press, 1981

39. D. Bauer and S.J. Bless, Strain Rate Effects on Ultimate Strain of Copper, Shock Waves in Condensed

Matter, North Holland, Amsterdam, 1983

40. G.R. Fowles, Experimental Technique and Instrumentation, Dynamic Response of Materials to Intense

Impulse Loading, P.C. Chou and A.K. Hopkins, Ed., Air Force Materials Laboratory, Wright-Patterson

Air Force Base, 1973

41. J.A. Zukas, T. Nicholas, H.F. Swift, L.B. Greszczuk, and D.R. Curran, Impact Dynamics, John Wiley &

Sons, New York, 1982, p 452

42. R.G. McQueen, S.P. Marsh, J.W. Taylor, J.N. Fritz, and W.J. Carter, The Equation of State of Solids

from Shock Wave Studies, High Velocity Impact Phenomena, R. Kinslow, Ed., Academic Press, 1970

43. S.P. Marsh, LASL Shock Hugoniot Data, University of California Press, 1980

44. L.M. Barker and E.G. Young, “SWAP-9: An Improved Stress Wave Analyzing Program,” Sandia

National Laboratories Report SLA-74-0009, Albuquerque, NM, 1974

45. U.S. Lindholm and L.M. Yeakley, High Strain Rate Testing: Tension and Compression, Exp. Mech.,

Vol 8, 1968, p 1–9

46. J. Harding, E.D. Wood, and J.D. Campbell, Tensile Testing of Material at Impact Rates of Strain, J.

Mech. Eng. Sci., Vol 2, 1960, p 88–96

47. C. Albertini and M. Montagnani, Testing Techniques Based on the Split Hopkinson Bar, Mechanical

Properties at High Rates of Strain, J. Harding, Ed., Institute of Physics, London, 1974

48. T. Nicholas, Tensile Testing of Materials at High Rates of Strain, Exp. Mech., Vol 21, 1980, p 177–185

49. P.W. Bridgeman, Chapter 1, Studies in Large Plastic Flow and Fracture, 1st ed., McGraw-Hill, 1952

50. L.A. Cross, S.J. Bless, A.M. Ranjendran, E.A. Strader, and D.S. Dawicke, New Technique to

Investigate Necking in a Tensile Hopkinson Bar, Exp. Mech., Vol 24 (No. 3), 1984, p 184–186

High Strain Rate Tension and Compression Tests

Rotating Wheel

Another method for tension testing at high strain rates consists of a rotating wheel with claws or noses that

quickly stroke a yoke containing test pieces. An early test machine was developed by Mann in 1936 (Ref 51),

and in 1944 Fehr et al. (Ref 52) reached strain rates of nearly 10

-1

with some bearable ringing. In the 1960s,

Schopper produced and sold about 100 “rotating wheel machines,” which also had a 200 kg (440 lb) wheel with

a releasable claw and a specimen within a yoke fixed in front of the wheel (Fig. 15). By careful adjustments,

velocities of about 40 m/s (130 ft/s) were reached without any bending moments. However, the overall

frequency response of the fixture (despite the 50 kHz quartz transducer for force-time recording) was only 2.5

kHz, which is too low for high-rate testing.

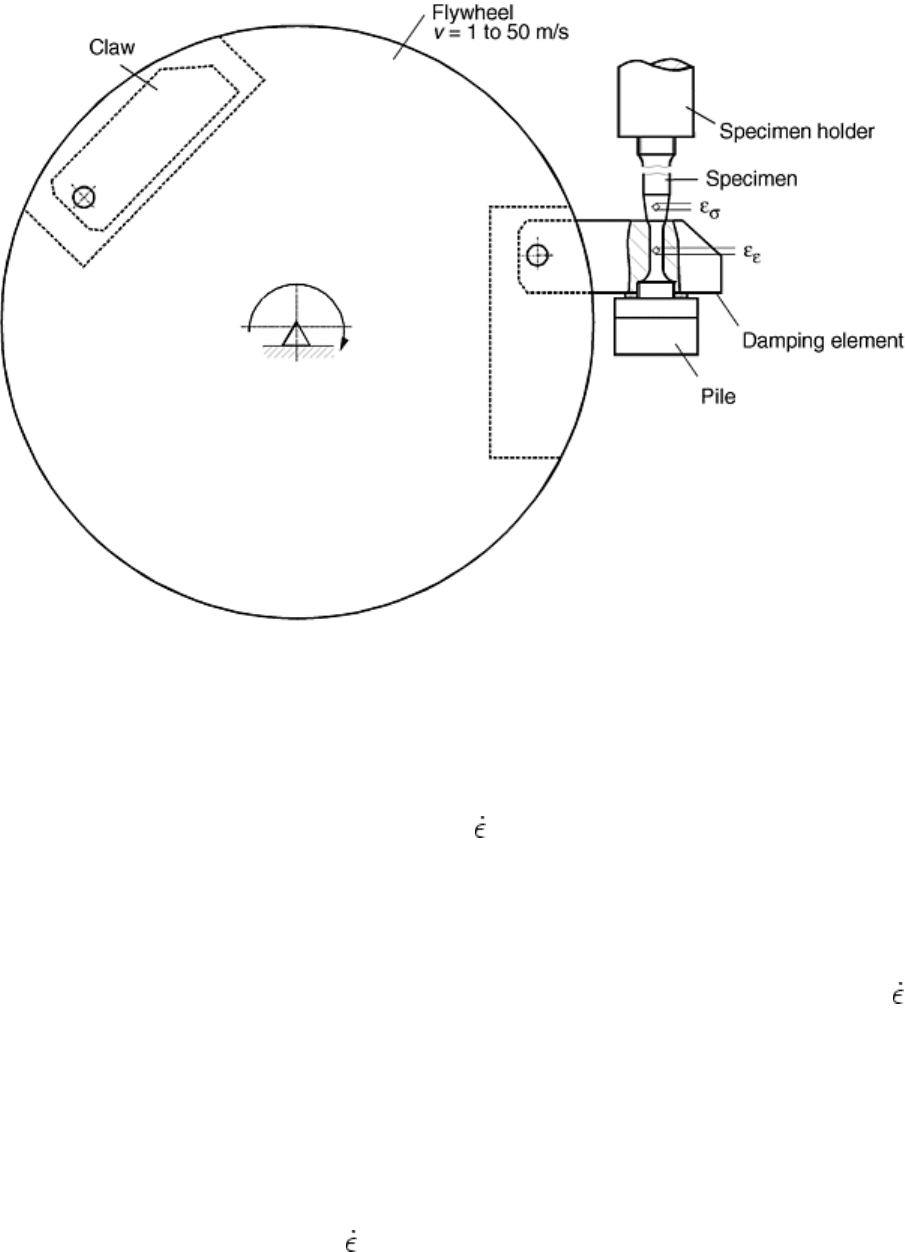
Fig. 15 Principle of high-rate tensile testing with flywheel setup

The essential improvement has been to introduce load-measuring gages as close to the gage length as possible.

This is realized by measuring elastic strains and converting to stresses by the elastic modulus. To assure low

barriers for reflections of stress wave propagation, the strain gages for load measurement are positioned at

cones of 8° on the smallest possible diameter. With this technique, stress-strain records are possible up to

velocities of 30 m/s, which corresponds to strain rates of = 2500 s

-1

with a gage length of 10.5 mm (0.41 in.)

and a diameter of 3.5 mm (0.14 in.) (L/D = 3). Even with high strain hardening and highly deformable

materials, there is practically no influence of the tested materials on the history of velocity or strain rate like in

a Hopkinson bar setup because the energy content of the rotating wheel exceeds the fracture energy of the

specimen more than 10 times (for striking velocities v > 10 m/s, or 33 ft/s).

A similar setup, but based on a moving mass of a few kilograms guided along straight bars, has also been

developed by Stelly and Dormeval at CEA, France with good results (Ref 53). Higher strain rates of = 10

-1

for example, can be reached with short gage length. To provide easy strain recording for the complete loading

up to fracture, electro-optical cameras or noncontact laser interferometers can be used. The advantage of this

instrumentation is that the strain is measured, not calculated under certain assumptions.

In order to avoid more reflections of the stress wave from the upper end of the specimen, the length beside the

gage length is extended to 2s > v

· t (where s is the rod length between gage length and fixture, v

is the sound

velocity, and t is the time to fracture at the used striking velocity). In the case of short lengths, a wave

transmitter bar is connected to the specimen. This procedure requires the evaluation of impedance transfer

between the sample and bar. Figure 16 shows stress-time diagrams of screwed, brazed, and welded joints tested

under high strain rate conditions at about = 1000 s

-1

. These results reveal that screwing and brazing are

insufficient methods to obtain stress-time diagrams of good quality. Therefore, in this test setup welded joints

are most suitable to perform tensile tests at high and very high strain rates.

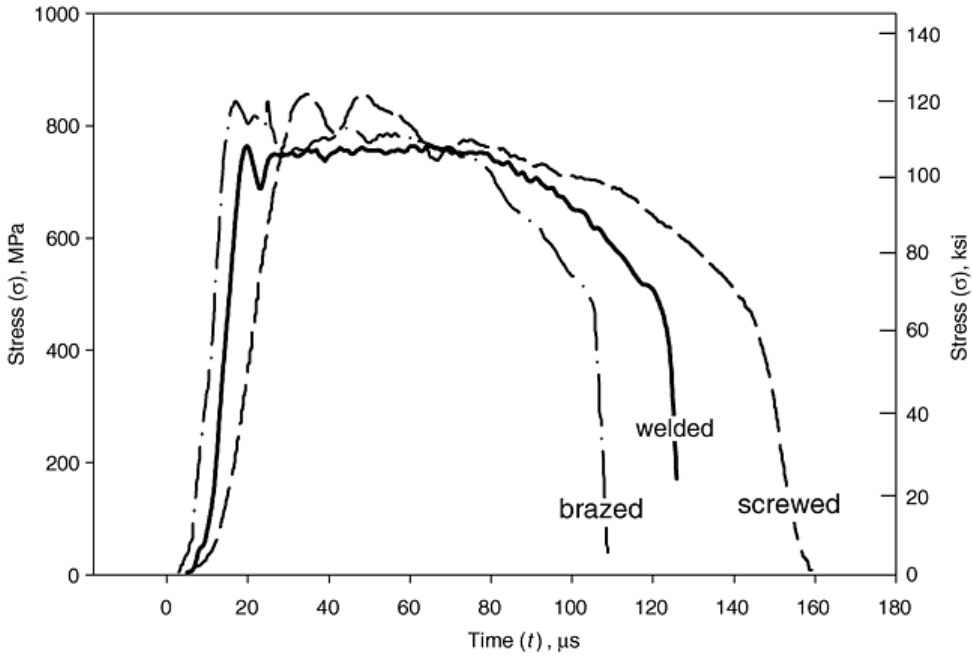
Fig. 16 Influence of joining method on stress-time curves for high strain rate tension test specimens

This procedure was successfully applied for high-rate, high-temperature tests (Fig. 17). Notice the occurrence

of the upper and lower yielding and the following nearly undisturbed stress-time records. The wave transmitter

bar was used for a stress measurement because the strain gages at the gage length were unsuitable at test

temperature. Temperatures up to 600 °C (1100 °F) are reached with heated air; higher temperatures should be

possible using small infrared ovens (Ref 54, 55) or induction heating.