ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation
Подождите немного. Документ загружается.


technique, it is possible to develop isothermal stress-strain curves for many materials at a desired temperature
and strain rate (Ref 7). This technique is described in the article “Recovery Hopkinson Bar Techniques.”
References cited in this section
1. J. Hopkinson, Original Papers by J. Hopkinson, Vol 2, B. Hopkinson, Ed., Cambridge: At the
University Press, 1901, p 316–324
2. B. Hopkinson, The Effects of Momentary Stresses in Metals, Proc. R. Soc. (London) A, Vol 74, 1905, p
498
3. B. Hopkinson, A Method of Measuring the Pressure Produced in the Detonation of High Explosives or
by the Impact of Bullets, Philos. Trans. R. Soc. (London) A, Vol 213, 1914, p 437–456
4. R.M. Davies, A Critical Study of the Hopkinson Pressure Bar, Philos. Trans. R. Soc. (London) A, Vol
240, 1948, p 375–457
5. H. Kolsky, An Investigation of the Mechanical Properties of Materials at Very High Rates of Loading,
Proc. Phys. Soc., Vol 62, 1949, p 676–700
6. S. Nemat-Nasser, J.B. Isaacs, and J.E. Starrett, Hopkinson Techniques for Dynamic Recovery
Experiments, Proc. R. Soc. (London) A, Vol 435, 1991, p 371–391
7. S. Nemat-Nasser and J.B. Isaacs, Direct Measurement of Isothermal Flow Stress of Metals at Elevated
Temperatures and High Strain Rates with Application to Ta and Ta-W Alloys, Acta Metall., Vol 45,
1997, p 907–919
Introduction to High Strain Rate Testing
Sia Nemat-Nasser, University of California, San Diego
Techniques Required for Split-Hopkinson Testing of Very Soft or Hard Materials
In order to render the split-Hopkinson technique useful and reliable for the testing of very soft and very hard
materials, special techniques must be used. These techniques are described in the articles “Split-Hopkinson
Pressure Bar Testing of Soft Materials”and “Split-Hopkinson Pressure Bar Testing of Ceramics,” respectively.
The Hopkinson technique can also be used to study the strain rate dependence of the compressive failure stress
of very hard materials. At room temperature, the strain in such a sample can be measured directly by attaching
strain gages to the sample (see the articles “Recovery Hopkinson Bar Techniques”and “Split-Hopkinson
Pressure Bar Testing of Ceramics”). For high-temperature tests new techniques are required, such as elevated-
temperature testing discussed in the article “Recovery Hopkinson Bar Techniques.”
The split-Hopkinson technique has also been extended to include testing ductile materials in tension, in torsion
(Ref 8, 9, 10, 11), and even in combined torsion and uniaxial stress (Ref 12). Torsional testing is described in
detail in the article “Torsional Kolsky Bar Testing.”The Hopkinson technique can also be used for high strain
rate indentation tests, as discussed in the article “Dynamic Indentation Testing.” another interesting
development based on the split-hopkinson bar is the deformation of a sample at high strain rates while it is
under a triaxial state of stress for both static and dynamic lateral confinement. (This is discussed in the article
“Triaxial Hopkinson Techniques.”)
For yet higher strain rates beyond the range of Hopkinson techniques (Fig. 1) other special techniques are
necessary. For very high strain rates, plate-impact experiments are used. The uniaxial Hopkinson experiments

provide a uniaxial stress in the sample (ideally speaking). The normal plate-impact experiment is designed to
provide a uniaxial strain state in the central portion of the sample. In the oblique plate impact experiment, the
uniaxial strain is accompanied by simple shearing. Strain rates of 10
5
and 10
6
s
-1
, and even greater, have been
achieved. This technique is discussed in the article “Low Velocity Impact Testing.” the strains that can be
produced by the plate impact experiments are, however, limited. To obtain large strains at high strain rates, one
may employ hat-shaped experiments and cylinder-collapse tests as described in the article “High Strain Rate
Shear Testing.”
References cited in this section
8. J. Harding, E.O. Wood, and J.D. Campbell, Tensile Testing of Materials at Impact Rates of Strain, J.
Mech. Eng. Sci., Vol 2, 1960, p 88–96
9. U.S. Lindholm, Some Experiments with the Split Hopkinson Pressure Bar, J. Mech. Phys. Solids, Vol
12, 1964, p 317–335
10. U.S. Lindholm and L.M. Yeakley, High Strain-Rate Testing: Tension and Compression, Exp. Mech.,
Vol 8, 1968, p 1–9
11. K.A. Hartley, J. Duffy, and R.H. Hawley, Measurement of the Temperature Profile During Shear Band
Formation in Steels Deforming at High Strain Rates, J. Mech. Phys. Solids, Vol 35, 1987, p 283–301
12. J.L. Lewis and W. Goldsmith, A Biaxial Split Hopkinson Bar for Simultaneous Torsion and
Compression, Rev. Sci. Instrum., Vol 44, 1979, p 812–814
Introduction to High Strain Rate Testing
Sia Nemat-Nasser, University of California, San Diego
References
1. J. Hopkinson, Original Papers by J. Hopkinson, Vol 2, B. Hopkinson, Ed., Cambridge: At the
University Press, 1901, p 316–324
2. B. Hopkinson, The Effects of Momentary Stresses in Metals, Proc. R. Soc. (London) A, Vol 74, 1905, p
498
3. B. Hopkinson, A Method of Measuring the Pressure Produced in the Detonation of High Explosives or
by the Impact of Bullets, Philos. Trans. R. Soc. (London) A, Vol 213, 1914, p 437–456
4. R.M. Davies, A Critical Study of the Hopkinson Pressure Bar, Philos. Trans. R. Soc. (London) A, Vol
240, 1948, p 375–457
5. H. Kolsky, An Investigation of the Mechanical Properties of Materials at Very High Rates of Loading,
Proc. Phys. Soc., Vol 62, 1949, p 676–700
6. S. Nemat-Nasser, J.B. Isaacs, and J.E. Starrett, Hopkinson Techniques for Dynamic Recovery
Experiments, Proc. R. Soc. (London) A, Vol 435, 1991, p 371–391

7. S. Nemat-Nasser and J.B. Isaacs, Direct Measurement of Isothermal Flow Stress of Metals at Elevated
Temperatures and High Strain Rates with Application to Ta and Ta-W Alloys, Acta Metall., Vol 45,
1997, p 907–919
8. J. Harding, E.O. Wood, and J.D. Campbell, Tensile Testing of Materials at Impact Rates of Strain, J.
Mech. Eng. Sci., Vol 2, 1960, p 88–96
9. U.S. Lindholm, Some Experiments with the Split Hopkinson Pressure Bar, J. Mech. Phys. Solids, Vol
12, 1964, p 317–335
10. U.S. Lindholm and L.M. Yeakley, High Strain-Rate Testing: Tension and Compression, Exp. Mech.,
Vol 8, 1968, p 1–9
11. K.A. Hartley, J. Duffy, and R.H. Hawley, Measurement of the Temperature Profile During Shear Band
Formation in Steels Deforming at High Strain Rates, J. Mech. Phys. Solids, Vol 35, 1987, p 283–301
12. J.L. Lewis and W. Goldsmith, A Biaxial Split Hopkinson Bar for Simultaneous Torsion and
Compression, Rev. Sci. Instrum., Vol 44, 1979, p 812–814
High Strain Rate Tension and Compression Tests
Introduction
MECHANICAL BEHAVIOR at high strain rates differs considerably from that observed at quasi-static or
intermediate strain rates, and many engineering applications require characterization of mechanical behavior
under dynamic conditions. For example, strain rates ranging from 100 s
-1
to more than 10
4
s
-1
occur in many
processes or events of practical importance, such as foreign object damage, explosive forming, earthquakes,
blast loading, structural impacts, terminal ballistics, and metalworking.
This introductory article briefly reviews the dynamic factors and experimental methods for high strain rate
tension testing and compression testing methods listed in Table 1. Considerable data on the high strain rate
behavior of many materials (including steels, aluminum and copper alloys, titanium, beryllium, magnesium,
and zinc) are available in the literature (see the Selected References at the end of this article). Results indicate
that for many metals a linear relation exists between flow stress and the logarithm of plastic strain rate in the
range from quasi-static rates to about 10
3
s
-1
. Above this range, however, the flow stress generally rises far
more rapidly with strain rate. Thus, the linear relationship is no longer valid, and extrapolation from the lower
strain rate regime becomes unreliable. Fewer data are available at the higher strain rates, particularly at very
high strain rates above 10
3
or 10
4
s
-1
, at which testing becomes more difficult. At strain rates in excess of 10
4
s
-
1
, the lower yield stress is often found to be directly proportional to strain rate, rather than to the logarithm of
strain rate. This implies a new region of mechanical response controlled in part by a viscous damping
mechanism in contrast to thermally activated processes at strain rates below 10
4
s
-1
.
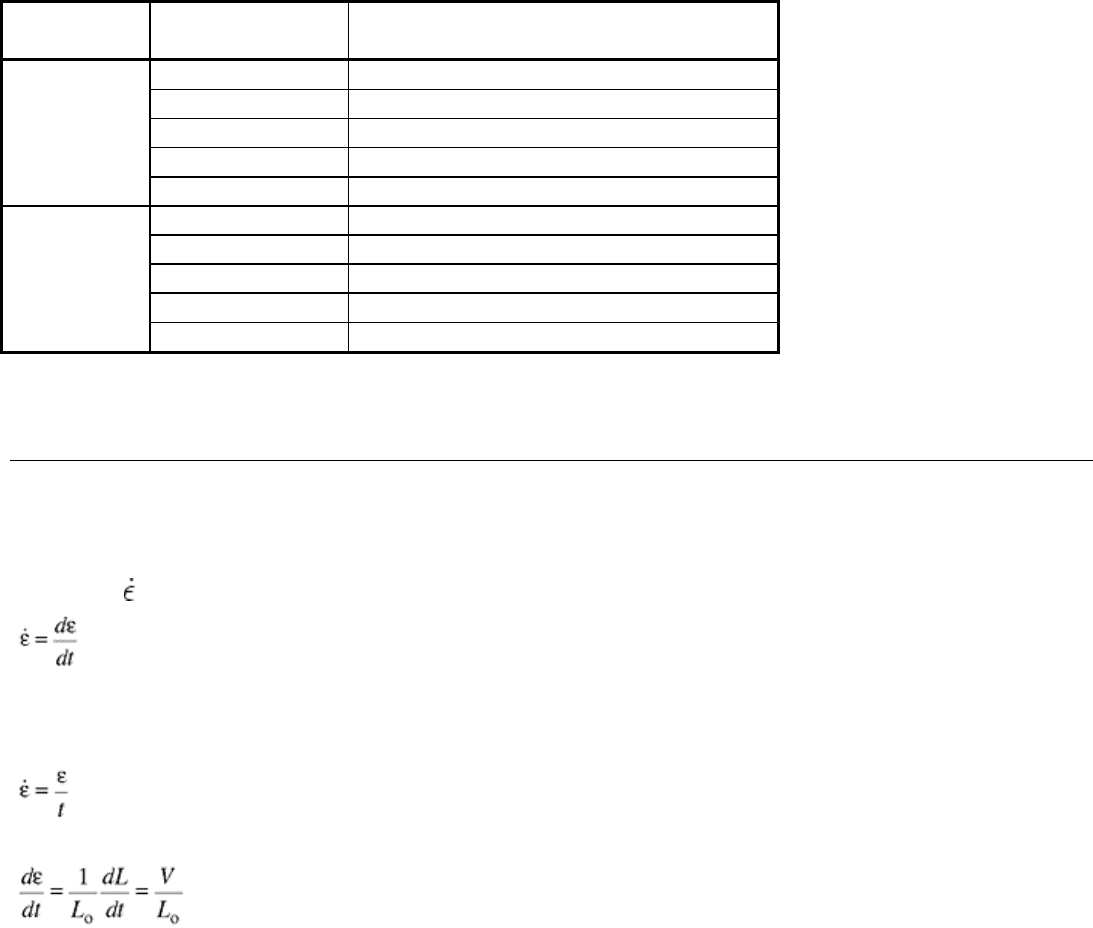
Table 1 Experimental methods for high strain rate testing
Mode Applicable strain
rate, s
-1
Testing technique
<0.1
Conventional load frames
0.1–100
Special servohydraulic frames
0.1–500
Cam plastometer and drop test
200–10
4
Hopkinson pressure bar in compression
Compression
10
4
–10
5
Taylor impact test
<0.1
Conventional load frames
0.1–100
Special servohydraulic frames
100–10
4
Hopkinson pressure bar in tension
10
4
Expanding ring
Tension
>10
5
Flyer plate
High Strain Rate Tension and Compression Tests
Test Effects at High Strain Rates
Strain rate, , is the rate of change of strain, ε, with time, t:
(Eq 1)
where ε can be either the engineering or the true strain. Although compressive strain and strain rate are negative
quantities, the negative sign is often omitted when it is understood that the test is a compression test. For a
constant strain rate experiment, the strain rate is simply the total strain divided by the duration of the test:
(Eq 2)
When ε in Eq 1 is the engineering strain, then:
(Eq 3)
where L is the length of the specimen of original length, L
o
, and V is the velocity at which the specimen is being
deformed. A constant crosshead speed in a mechanical testing machine yields a constant engineering strain rate
defined by Eq 3.
A typical (quasi-static) mechanical test is performed at a strain rate of around 10
-3
s
-1
, which yields a strain of
0.5 in 500 seconds. The equipment and techniques generally can be extended to strain rates as high as 0.1 s
-1
without difficulty. Tests at higher strain rates may necessitate other experimental techniques and additional
dynamic considerations, such as inertia effects, wave propagation effects, and shock wave effects (Fig. 1).
Thermal effects and the difficulties of strain measurement are additional factors in high strain rate testing.
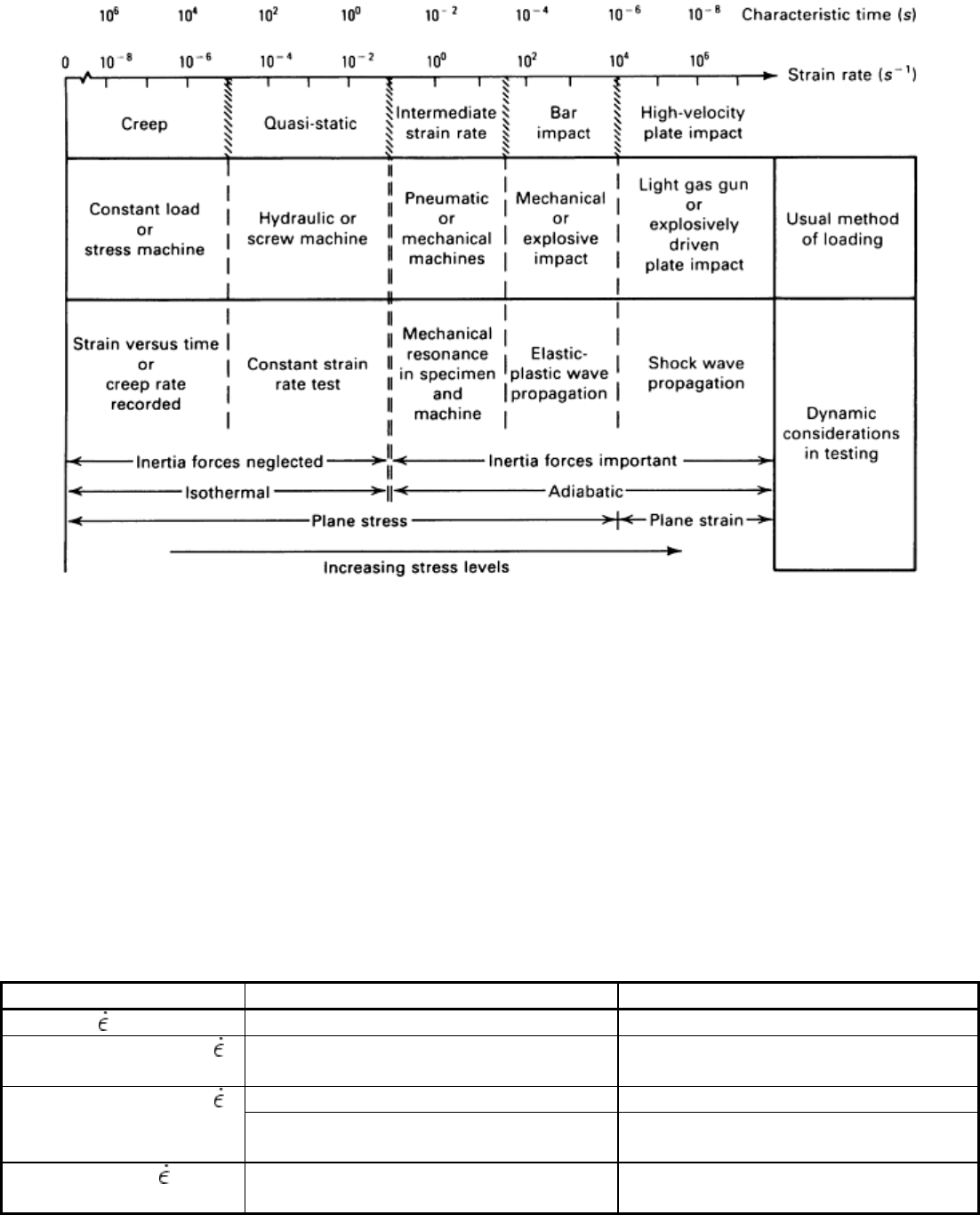
Fig. 1 Dynamic aspects of materials testing. Source: Ref 1
Dynamic Factors
A fundamental difference between a high strain rate test and a quasi-static test is that inertia and wave
propagation effects become more pronounced at higher strain rates (Fig. 1). These dynamic effects on test
results become more pronounced at higher strain rates, as shown in Table 2, for low, medium, high, and very
high strain rate regimes. When the strain rate is increased through the medium strain rate regime, the
measurement of load is the first to be affected by stress wave propagation. As the strain rate is increased even
further, uniform deformation within the specimen becomes more critical. At very high strain rates (beginning at
about 10
4
or 10
5
s
-1
), shock wave propagation becomes critical. Shock wave propagation is discussed in more
detail in the article “Shock Wave Testing of Ductile Materials” in this Volume.
Table 2 Experimental techniques for various strain rate regimes in compression testing
Strain rate regime Experimental techniques
Wave propagation
Low rate: < 0.1 s
-1
Standard mechanical testing procedures
Not significant
Medium rate: 0.1 s
-1
≤ ≤
200 s
-1
Servo-hydraulic frames, cam
plastometer, drop test
Influences load measurement
Hopkinson pressure bar
Affects uniform stress approximation
High rate: 200 s
-1
≤ ≤
10
5
s
-1
Rod impact (Taylor) test
Analysis required for interpretation
of results
Very high rate: > 10
5
s
-
1
Flyer plate impact Critical
Source: Ref 2
Conventional Load Frames at Medium Strain Rates. Strain rate effects in uniaxial tension or compression are
determined by tests with conventional load frames up to approximately 100 or 200 s
-1
. Conventional test
machines are available with increased ram velocities, as are high-speed pneumatic and hydraulic machines. The
speed capability of a machine may be influenced by several factors. Speed may be a function of the load that
the ram is attempting to apply, and the no-load speed may be much higher than the full-load speed. The
distance traveled may also affect the speed capability. A long-stroke machine may attain a given speed only
after a significant amount of travel. Depending on the specimen length, considerable specimen strain could
occur before final maximum velocity is obtained in a tension test. Finally, the ability to control speed is a
function of the response capability of a servo-controlled machine working in a closed-loop mode. Open-loop
machines provide speeds that can be influenced by specimen strength and cannot easily reproduce
predetermined velocities or strain rates on materials with different yield strengths or strain hardening behaviors.
Load cell ringing at intermediate or medium strain rates may be negligible. However, even if wave propagation
effects in the test piece can be neglected, the characteristic response time of load cells must still be checked. At
intermediate strain rates, “ringing” of a load cell can mask the desired measurement. Load cell ringing is
frequently encountered in high-rate tensile testing. Generally, the load-cell response time (which is the
reciprocal of its natural frequency in hertz) must be small compared to the total duration of the test. For
example, if a load cell has a natural frequency of 1 kHz, its period of vibration is 10
-3
s. This load cell could
then be used only for experiments that lasted over ten times that amount, or over 10 μs.
Another condition that must be satisfied is the distance of the load cell from the end of the specimen. If a
sufficient distance exists between the specimen and load cell, the finite elastic wave transit time may result in
load data that are not time-coincident with strain data. To prevent phase lags from obscuring the experimental
data, the wave transit time from the specimen to load cell should be negligibly small compared to the test
duration. Otherwise, the load data must be corrected for the delay, and such corrections seldom are precise.
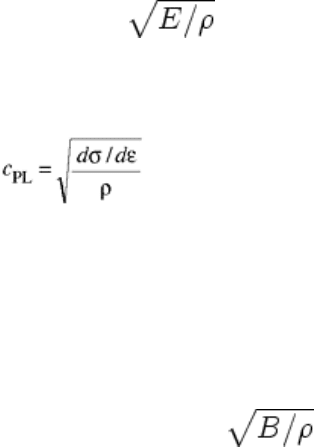
Wave Propagation Effects. At high strain rates, uniform deformation within the test piece becomes a factor.
Inertia initially opposes uniform deformation, and a stress wave is transmitted and reflected within the test
piece at the speed of sound. If the deformation is purely elastic, then the longitudinal sound velocity, c
EL
, is
simply c
EL
= , where E is the elastic modulus and ρ is density. If the material has deformed into the
plastic region, the plastic-wave velocity is more appropriate and generally can be an order of magnitude smaller
than the elastic wave velocity. One-dimensional strain-rate-independent theory predicts that the plastic wave
propagates at a velocity, c
PL
, determined by:
(Eq 4)
where dσ/dε is the slope of the true stress/true strain curve. For many materials, the initial work-hardening rate
dσ/dε is approximately 1% of E; thus for these materials, the plastic wave velocity is approximately 10% of the
elastic-wave velocity.
However, experimental evidence in a variety of metals suggests that the above estimate is too conservative. The
stress waves generated by impacts at stress levels far in excess of the yield stress appear to travel, at least
initially, closer to the elastic wave velocity rather than at the plastic wave velocity (Eq 4). This implies that the
wave propagation behavior can be more complicated than described by Eq 4. The velocity of the plastic wave is
sometimes estimated as where B is the bulk modulus.
The velocity of waves and the size of the test piece determine the upper limit of strain rate for accurate
measurement of stress-strain curves. If many wave transits occur during a test, the use of average stresses and
strains can be justified. However, if only a few wave reflections occur before the specimen fails, then individual
wave propagation must be considered. In this case, average values alone cannot be considered, and the use of
this test to determine dynamic stress-strain response is precluded. As a first approximation, Davies and Hunter
(Ref 3): have estimated that three reverberations are required for stress equilibration in compression testing.
To illustrate the importance of stress wave propagation, consider compression testing of a 10 mm (0.4 in.)
specimen, in which the elastic wave velocity is 5.0 × 10
3
m/s (16.4 × 10
3
ft/s) and the initial plastic wave
velocity may be approximated as 5.0 × 10
2
m/s (16.4 × 10
2
ft/s). Assuming that three reverberations of the
slower moving plastic wave are required for uniform stress within the deforming specimen, the time for these
reverberations is computed to equal 60 μs. At a strain rate of 10
3
s
-1
, the specimen will have compressed to a
strain of 6% during this interval. Thus, data at strains less than this may be invalid, because it cannot be
assumed that the specimen was deforming uniformly. Even if the elastic wave velocity is used in the above
example, the critical strain at which uniform stress within the specimen is achieved is computed to be equal to
0.6%. At a strain rate of 10
4
s
-1
, this critical strain becomes 6%.

The above example illustrates that wave propagation becomes an important consideration affecting test validity
in the high strain rate regime of Table 2. It also illustrates a major advantage of compression testing over
tension testing at high strain rates; a compression test specimen can be fabricated to relatively small dimensions
to minimize wave propagation times. Another way to determine whether or not wave propagation effects limit
the validity of a test is the sample ring-up time, which is the time required for a sample to achieve a uniform
state of stress. Generally, measurements are not valid for times such that L ~ ct, where c is the speed of stress
wave propagation. This corresponds to a situation in which strain ε >> L/c. Consequently, small strain
measurements are difficult to obtain at very high strain rates. Sample length can also be reduced, although there
are limits in reducing specimen dimensions.
Another concern is that local failure may occur at the end to which the load is applied. The magnitude of the
stress transient (σ
m
) associated with the sudden application of velocity v
0
is σ
m
= ρcv
0
(where ρ is density of the
material). Tension tests must be designed so that σ
m
< σ
yy
, the tensile yield stress. For example, consider a bar
25 mm (1 in.) in length that is accelerated at one end to 2.5 m/s (8.2 ft/s). For many engineering materials,
including steels, aluminum alloys, and titanium alloys, the elastic wave velocity is about 5000 m/s (16,400 ft/s).
The maximum stress generated at the accelerated end of the bar is ρcv, where v is the deformation speed (v =
L). For a steel bar, the first stress pulse is 100 MPa (14.5 ksi) and the average strain rate is 100 s
-1
. If a steel
with a strength of 1 GPa (145 ksi) is being tension tested, the maximum allowable driving velocity is 25 m/s
(82 ft/s). At that velocity, instantaneous failure would occur at the driven end.
Departure from Isothermal Test Conditions
It is well known that most of the work of deformation is expended as heat; only 5 to 10% of this work is
actually stored in the defect structure of the deformed specimen. As the strain rate increases, there is
insufficient time for the transport of this heat from the specimen to the grips, platens, or atmosphere. Thus, the
specimen temperature can increase during deformation.
The work of deformation, W, is simply:
W = P dL
(Eq 5)
where P is the applied load, and L is the length of the specimen of final length, L
f
, and original length, L
o
.
Equation 5 can be rewritten as:
W = A
o
L
o
s(e)de
(Eq 6)
where A
o
and L
o
are the original specimen area and length, respectively, s is the engineering stress, and e is the
engineering strain.
If it is assumed that this work is transformed to heat adiabatically (i.e., without heat flow), then the specimen
temperature increase, ΔT, is defined by:
(Eq 7)
where ρ is the density, and C
p
is the heat capacity of the test piece material at constant pressure. As an example,
consider the deformation of a stainless steel specimen to a strain of 0.5, and, for simplicity, also assume that the
flow stress of the material is constant and equal to 750 MPa (109 ksi). With a density of 8 g/cm
3
(0.29 lb/in.
3
)
and a heat capacity of 500 J/kg · K (0.120 cal/g · °C), the temperature increase at a strain of 0.5 is estimated to
be 94 K calculated from Eq 7. This is a significant increase and demonstrates that this is not an isothermal test.
The above estimate assumed adiabatic conditions, which are only the case in the high strain rate regime.
However, at least under these conditions, the temperature increase can be estimated fairly accurately, and
deformation within the specimen remains uniform. The medium strain rate regime is further complicated by
heat flow, which in quiescent environments is dominated by conduction through the ends of the specimen. In
this regime, there is the possibility of generating a substantial axial temperature gradient from the end to the
midpoint of the specimen. This gradient can result in nonuniform deformation throughout the specimen, which
complicates interpretation of the experimental results. In fact, if the temperature dependence of the flow stress
is high enough, deformation may become highly localized at the center of the specimen; this situation is less
likely in a compression specimen than it is in a tensile specimen, which has a much higher aspect ratio.
Measurement of Stress and Strain
Measurement of stress and strain and data acquisition becomes more difficult as the strain rate increases. For
example, the frequency response of the load cell must be considered, as previously noted. The frequency
response of other measurement devices, such as extensometers or strain gages, must also be considered, along
with any signal conditioning and the sampling rates during digital data acquisition. Computer data acquisition
systems with sampling at rates as fast as 100 kHz should be sufficient for tests at strain rates as high as 10
2
s
-1
.
For analog-to-digital processing, the sampling rate is inversely related to the desired accuracy or byte size of the
digitized “word.” For example, with a byte size of 10 bits, sampling rates with typical processors can be as fast
as 20 MHz.
In some cases, the standard measurement techniques for stress or strain at low strain rates become unsuitable
for testing at higher strain rates. For example, the use of fragile devices, such as extensometers, may not be
appropriate for tests that involve large, rapid deformations. Specific procedures for each of the experimental
techniques are discussed in more detail in the following sections, but a few general comments concerning strain
measurement during tension tests with conventional load frames are summarized here. Additional information
on compression testing at medium strain rates is also in the article “Uniaxial Compression Testing” in this
Volume.
Measurement of strain is a major problem in high strain rate testing. In quasi-static tension testing, for example,
the diameter of the minimum cross section in a cylindrical specimen is easily measured. In contrast, such
measurements are virtually impossible or highly impractical in high-rate testing. Furthermore, although strains
are easily measured over a uniform gage length section in quasi-static tension testing, the same measurements
are considerably more difficult to obtain at high strain rates. Mechanical extensometers also are of little use at
high strain rates due to the effects of inertia.
In high strain rate tests, strain measurements typically utilize strain gages, optical extensometers, and
displacement measurements between loading fixtures to determine or infer the dynamic tensile in a test piece.
At very high rates of strain, strains may be measured in some experimental configurations only through wave
propagation analysis. This procedure generally requires that assumptions be made about the constitutive
behavior, that wave propagation analysis be carried out, and that predictions and experimental observations be
compared. Unique solutions cannot be guaranteed because some other constitutive model may conceivably
provide similar results in a particular wave propagation problem.
Electrical resistance strain gages are the most direct, reliable method for strain measurement in high-speed
testing. The frequency response capability of strain gages is considerably greater than the mechanical response
of the combination of load train, specimen, and load cell. Another method of measuring strain involves the use
of optical extensometers, in which displacement measurements across the loading fixtures are divided by an
actual or effective gage length. When using crosshead displacement in tension test, caution must be exercised to
ensure that these represent only specimen elongation and not machine, ram, or load train elongations. The same
precautions that apply in quasi-static tests also apply in dynamic tests. If these precautions are observed, valid
stress-strain data from tension testing in conventional load frames can be obtained up to maximum strain rates
in the range of 10 to 100 s
-1
. For higher strain rates, or for cases in which the above criteria are not met, more
specialized testing techniques may have to be used, as discussed in this article and in the remaining articles in
this Section.
References cited in this section
1. U.S. Lindholm, High Strain Rate Tests, Measurement of Mechanical Properties, Vol 5, Part I,
Techniques of Metals Research, R.F. Bunshah, Ed., Interscience, 1971, p 199–271
2. High Strain Rate Compression Testing, Mechanical Testing, Vol 8, ASM Handbook, ASM International,
1985 p 190–207
3. E.D.H. Davies and S.C. Hunter, The Dynamic Compression Testing of Solids by the Method of the Split
Hopkinson Pressure Bar, J. Mech. Phys. Solids, Vol 11, 1963, p 155

High Strain Rate Tension and Compression Tests
Compression Tests at High Strain Rates
As listed in Tables 1 and 2, several methods are available for compression testing at strain rates up to about 10
4
to 10
5
s
-1
. These high strain rate compression tests are briefly reviewed in this section with a focus on the
general principles, advantages, and limitations of each test method.
Cam Plastometer
The cam plastometer is designed specifically for compression testing at strain rates from 0.5 to more than 200 s
-
1
. The axial load to compress the specimen is transferred from massive rotating flywheels through a cam; this
provides the distinct advantage of being able to obtain a constant true strain rate experiment. The cam
plastometer is used to obtain the resistance to compressive deformation of materials, principally metals, at
constant strain rates over a useful and significant range of strain rates and a practical range of testing
temperatures. Most plastometers have a capacity to compress cylindrical specimens homogeneously to a 50%
reduction in height, assuming the material is tested at temperatures at which it is ductile enough to permit this
reduction.
The development of the cam plastometer in the 1950s was significant because it allowed an extension of
mechanical testing capability by three orders of magnitude in strain rate over that obtained in standard
mechanical test machines. Furthermore, the cam plastometer mechanism lends itself to the generation of a
constant true strain rate experiment, which is ideally suited for metal deformation studies. Most cam
plastometer facilities have elevated-temperature testing capabilities. Some of these are equipped for testing in
vacuum or in selected atmospheres. These require a vacuum chamber around the specimen-platen assembly and
the use of O-ring or bellows grips. The elevated-temperature capability for some facilities is up to 1300 K
through the use of in situ induction heating in a reducing atmosphere and the use of aluminum oxide platens.
These platens appear to dampen some load cell ringing that occurs when using much denser tungsten carbide
platens.
The cam plastometer was originally used to study the rolling characteristics of uranium plate and sheet by the
classic Orowan method (Ref 4). This machine underwent several revisions in both mechanical design and
instrumentation for compression testing of pure lead (Ref 5), commercial-purity aluminum (Ref 6), and steels
(Ref 7). The first constant true strain rate cam plastometer was designed and built by Orowan at the British Iron
and Steel Research Association (BISRA) in 1950. It was used to obtain true stress-strain curves for 12 steels at
true strain rates of 0.05 to 100 s
-1
and temperatures from 1173 to 1473 K (Ref 7). Others have built cam
plastometers to perform specific studies. Machines have been built to study the compressive deformation of
aluminum and aluminum alloys (Ref 8, 9), depleted uranium (Ref 4, 10), zinc and zinc alloys (Ref 11, 12), and
other ferrous and nonferrous metals (Ref 13). A modern version of the cam plastometer has also been designed
and built at the Canadian Department of Mines, Energy, and Resources (Ref 14).
True strain rate compression tests are achieved in all cam plastometers by designing the load-applying
mechanism in the form of a logarithmic cam (as true strain is, by definition, logarithmic strain). The true strain
rate is constant only if the rotational speed of the cam is constant. This is achieved by storing large amounts of
energy in flywheels and in the many rotating parts of transmissions, as well as in the cam. To maintain a
constant strain rate, this stored energy must greatly exceed the energy required to compress the specimen. A
typical cam plastometer setup is shown in Fig. 2, in which a 37 kW direct-current motor (behind the belt guard)
and the 40 kV generator are depicted. The motor drives three flywheels distributed between and at both ends of
the drive train, which consists of two large off-highway-type transmissions. Cam plastometers can be massive
pieces of equipment. Size introduces problems in dynamically balancing the cam and in providing sufficient
strength and minimum deflection of the loading frame and drive train. Some cam plastometers in Japan have
been equipped with four-post loading frames to circumvent these problems.

Fig. 2 Typical cam plastometer facility. Direct-current motor and generator are on the left; three
flywheels and two transmissions are on the right; two-post loading frame is at rear. Courtesy of Los
Alamos National Laboratory
Effects of Friction and Lubricants. As in all compression tests, deformation is homogeneous throughout the test
only if frictional constraint is minimized at the interfaces between the platens and the specimen ends. That is,
the specimen should start out as a cylinder and maintain this cylindrical geometry throughout the test. This
requires the use of a suitable lubricant at the interfaces.
Minimizing the effects of friction in a compression test involves selection of a suitable length-to-diameter (L/D)
ratio for the specimen and the selection of proper lubrication for the specimen/platen interfaces. An L/D ratio of
1.56 is generally considered optimum. Ratios much larger than this lead to buckling, whereas ratios much
smaller than this yield higher stress-strain curves, indicating excessive specimen-platen frictional constraint. An
L/D ratio of 1.56 is within the range specified in ASTM E 9, “Compression Testing of Metallic Materials at
Room Temperature.”
Many lubricants (e.g., viscous oils, powdered graphite, or powdered, liquid-based, and grease-based
molybdenum disulfide) have been used for room-temperature testing. A satisfactory lubricant for room-
temperature and lower-temperature (to 77 K) testing is “Motor-Mica,” which is a mixture of finely ground
powdered mica and a highly viscous commercial automotive oil.
At slightly elevated temperatures, powdered tungsten disulfide has been used successfully. At higher
temperatures, various glass frits exhibiting viscosities in the range 4000 to 6000 Pa · s (400–600 poise) at
temperature can be used. For a series of tests on a titanium alloy, the commercial glaze Deltaglaze 347m was
used above 1283 K, and Deltaglaze 349m has been used between 900 and 1010 °C (1650 and 1850 °F).
Coefficient of friction measurements by the method proposed in Ref 15 may be helpful in the preliminary
selection of lubricants. Concentric grooves in the ends of the specimen are necessary for most plastometer
testing. Depth, spacing, and included angle of the grooves must be determined empirically.
