ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

Other Parameters. The Manson-Haferd parameter predicts a constant stress plot from log time, t, versus

temperature, T (in °F, °C, or K), from the parametric relation:

This equation yields a family of straight lines converging to a point t(T

, t

), which defines the optimum

constants for that particular data set (Fig. 6b). On these same coordinates, the Manson-Succop parameter

requires that isostress lines be straight and parallel (Fig. 6d). These conflicting patterns and still different

patterns for the additional parameters cannot occur simultaneously over the entire range of data from a given

set.

A frequent finding is that different parameters provide best fit to different portions of the same data. For

example, using data obtained from tests on a 1Cr-1Mo-0.25V steel, the Larson-Miller parameter gave the best

extrapolation at 482 °C (900 °F), and the Manson-Haferd parameter was preferable at 538 °F (1000 °F).

However, the Orr-Sherby-Dorn parameter gave the best fit at 593 °C (1100 °F) (Ref 35, 36).

Although numerous studies have considered the relative merits of these and other proposed parameters, no one

parameter has emerged as universally superior to all others. Five representative parameters were compared in

terms of correlating and extrapolating extensive sets of data on the creep and rupture properties of seven steels

and superalloys (Cr-Mo, Cr-Mo-V, 12%Cr, A 286, Astroloy, René 41, and Inconel 718) (Ref 37). The

difference in fit among parameter methods was found to be relatively small and inconsistent from one alloy to

another. The largest source of variation in the fitted values for time to rupture, time to 1% creep, and minimum

creep rate was the difference between alloys, regardless of the parameter used.

Results were marginal to poor when extrapolation was beyond the range of the fitted master curve. When

prediction of long-time data was confined to the master curve derived using only short-time data, no one

parametric method gave consistently superior results.

For critical evaluation of the comparative ability to predict known long-time rupture lives (11,000–64,000 h)

for the ferritic steels, data up to 10,000 h were applied to establish fit to the parametric model. For the

superalloys, only data up to 1000 h were used to predict known rupture times between 1200 and 33,000 h.

Table 1 lists ranges for the ratio (predicted life/actual life) extracted from Ref 37 for 46 extrapolations,

including one in which slight extension was required beyond the fit of each master curve.

Table 1 Comparative extrapolation abilities of methods used to determine creep-rupture behavior

Ratio: predicted life/actual life

Parameter

or method

Minimum

Average

Maximum

Larson-Miller 0.34 1.57

5.64

Manson-Haferd 0.44 1.51

6.30

Goldhoff-Sherby 0.36 1.64

8.85

Manson-Succop 0.39 1.53

4.96

Orr-Sherby-Dorn 0.11 1.09

4.01

Monkman-Grant

0.33 0.93 1.82

Studies on 0.5Cr-0.5Mo-0.25V steel pipe (Ref 38) found the Manson-Haferd parameter significantly superior to

predict known rupture times (8712–20,664 h) from data points of less than 6000 h duration than either the

Larson-Miller or Orr-Sherby-Dorn parameters. The latter two parameters generally provide optimistic

prediction of behavior. According to Ref 38, very short-time data should be eliminated from the analysis if

predictions beyond 10,000 h are desired, because their inclusion distorts the correlation at long times. As with

graphical methods, the accuracy of parametric extrapolations is related to the interval of test variables on which

the prediction is based.

Minimum Commitment Method. Experimental data may deviate from the requirement imposed by the form of

each parameter for linearity of isostress curves or for parallelism or convergence of families of such curves. The

minimum commitment method starts with a time-temperature-stress relationship sufficiently general to include

all commonly used parameters. The pattern of the data is not forced in advance; instead, the actual experimental

data naturally lead to the most appropriate functional relationship for the particular material.

Manson applied a “station-function” approach to f(log t) + p(T) = g(σ); all parametric formulations can reduce

to this equation. Each of the functions f, p, and g were represented by their discrete numerical magnitudes at

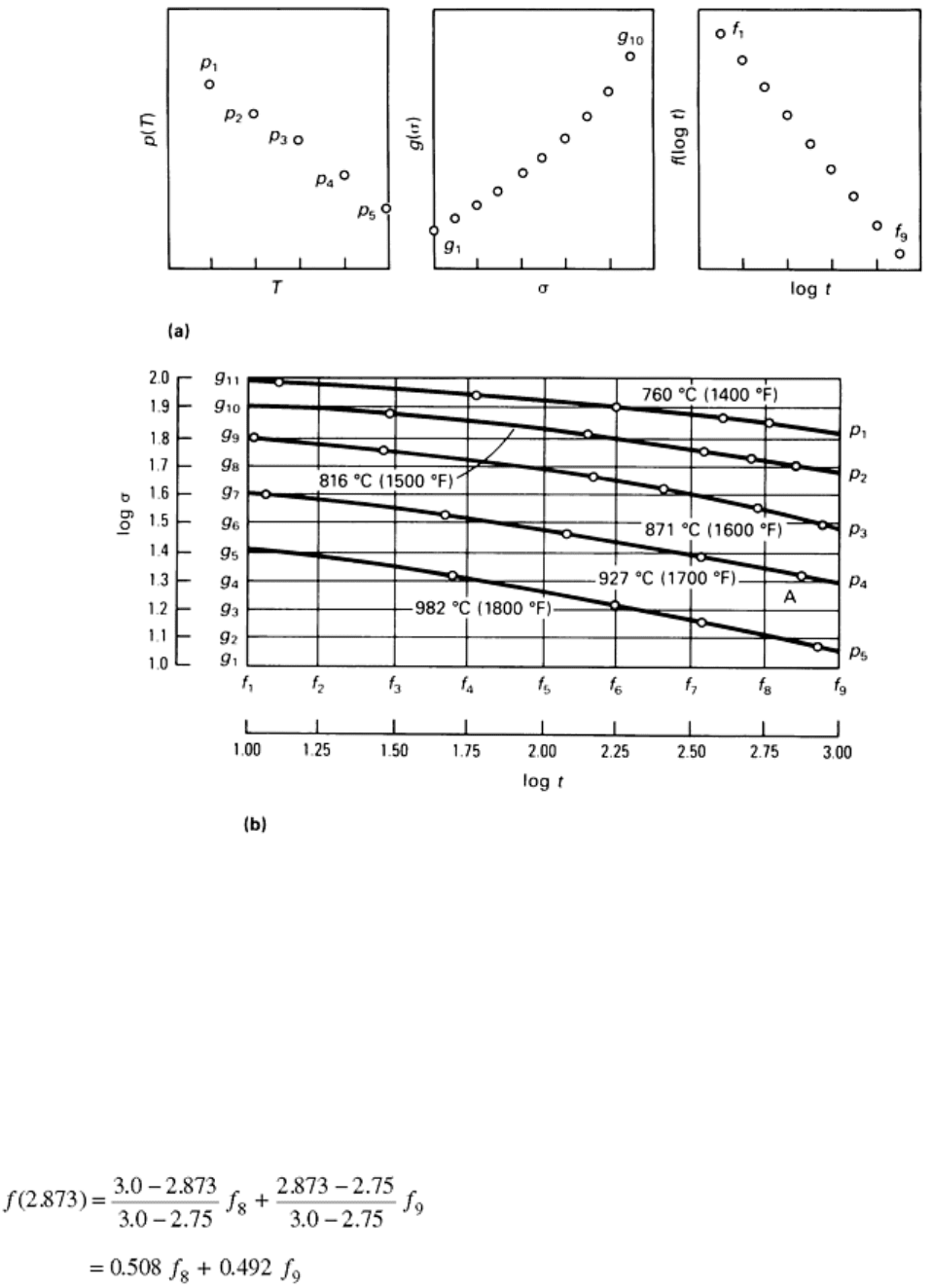
specific values of the corresponding independent variable. Figure 8 illustrates treatment of Astroloy data given

in Ref 37.

Fig. 8 Application of station function approach to Astroloy data. (a) Station-function representation of

p(T), g(σ), and f(log t) at specific values of T, σ, and log t. (b) Net point selections for solution. Source: Ref

Temperature stations were arbitrarily chosen at T = 760, 816, 871, 927, and 982 °C (1400, 1500, 1600, 1700,

and 1800 °F); the values of the p functions at these respective temperatures are designated p

, p

, and p

For times such that log t = 1.0, 1.25, 1.5, …, 3.0, the respective corresponding f values are f

, f

, …, f

. The g

values are designated g

, g

, …, g

for levels of log σ = 1.0, 1.1, 1.2, …, 2.0, with σ given in ksi.

Consider the experimental point A (T = 927 °C, or 1700 °F); log t = 2.873, log σ = 1.322). At this point, p is

directly p

, but values of f and g must be interpolated. Higher order interpolation can be easily accomplished,

but simple linear interpolation was chosen for this illustration. For A between log t of f

= 2.75 and f

= 3.00:

(Eq 3)

In a similar manner, the relation for stress at this point becomes:

(Eq 4)

Introducing these results into the original general equation yields:

0.508 f

+ 0.492 f

+ p

= 0.78 g

+ 0.22 g

(Eq 5)

A similar equation can be written for each experimental point. By choosing a sufficient number of stations, the

number of equations available will exceed the number of unknowns, so that a least-squares solution can be used

to determine the unknowns. Once the equations have been solved, the function f(log t) may be extrapolated

using graphical, polynomial, or recurrence relations.

Although a better fit to the data should result by the minimum commitment method than by forcing fit to an

arbitrary parameter, extrapolations can still be imprecise. As with other methods, the degree of accuracy of

predictions relies on having accurate and representative raw data from tests that reflect any structural changes

expected to occur in the regime of the extrapolated conditions.

A specialized form of the general equation developed in 1971 (Ref 40) contains a characteristic material

constant A:

log t + AP(T) log t + P(T) = G(log σ)

(Eq 6)

The parameter A is a measure of structural stability, because the more unstable the material, the higher the

negative value of A required to fit the data. On a plot of log stress versus log time, all isothermals converge at

the extrapolated point log t = -(1/A) (Ref 41). For the parallel isotherms of the Orr-Sherby-Dorn parameter, A =

0; Miller-Larson requires A = +0.5. With data fitting the Manson-Haferd parameter, negative A values result;

the Astroloy data discussed above converge at about t = 6.36, resulting in A = -0.157.

Establishing an accurate individualized value of A for a specific material is difficult from a short-life database.

One acceptable approach is to use universalized values of A = 0 for aluminum alloys and pure metals, and A = -

0.05 for most steels and superalloys (Ref 41). Highly unstable materials like Astroloy, as well as carbon steels,

require higher negative values of A; for these materials, A = -0.15 was found to be adequate in most instances.

The minimum commitment method was initially developed for use with single-heat data. Application to

multiple-heat analyses is discussed in Ref 42, including information on suitable computer programs.

References cited in this section

23. R.L. Klueh, Interaction Solid Solution Hardening in 2.25 Cr-1Mo Steel, Mat. Sci. Eng., Vol 35, 1978, p

239–253

28. J.H. Bennewitz, On the Shape of the Log Stress-Log Time Curve of Long Time Creep-Rupture Tests,

Joint International Conference on Creep, Institute of Mechanical Engineers, London, 1963, p 5-81 to 5-

29. W.C. Leslie, J.W. Jones, and H.R. Voorhees, Long-Time Creep-Rupture Tests of Aluminum Alloys, J.

Test. Eval., Vol 8 (No. 1), 1980, p 32–41

30. D.J. Wilson and H.R. Voorhees, Creep Rupture Testing of Aluminum Alloys to 100,000 Hours, J. Mat.,

Vol 7 (No. 4), 1972, p 501–509

31. S.P. Agrawal, L.E. Byrnes, J.A. Yaker, and W.C. Leslie, Creep Rupture Testing of Aluminum Alloys:

Metallographic Studies of Fractured Test Specimens, J. Test. Eval., Vol 5 (No. 3), May 1977, p 161–

173

32. D.J. Wilson, Extrapolation of Rupture Data for Type 304 (18Cr-10Ni), Grade 22 (2- Cr-1Mo), and

Grade 11 (1- Cr- Mo- Si) Steels,” Trans. ASME J. Eng. Mat. Technol., Jan 1974, p 22–33

34. F.R. Larson and J. Miller, A Time-Temperature Relationship for Rupture and Creep Stresses, Trans.

ASME, Vol 74, 1952, p 765

35. R.M. Goldhoff, Comparison of Parameter Methods for Extrapolating High-Temperature Data, Trans.

ASME J. Basic Eng., Vol 81 (No. 4), Series D, Dec 1959, p 629–644

36. R.L. Orr, O.D. Sherby, and J.E. Dorn, Correlations of Rupture Data for Metals at Elevated

Temperatures, Trans. ASM, Vol 46, 1954, p 113–118

37. R.M. Goldhoff and G.J. Hahn, Correlation and Extrapolation of Creep-Rupture Data of Several Steels

and Superalloys Using Time-Temperature Parameters, in Time-Temperature Parameters for Creep-

Rupture Analysis, American Society for Metals, 1968, p 199–245

38. W.M. Cummings and R.H. King, Extrapolation of Creep Strain and Rupture Properties of Cr- Mo- V

Pipe Steel, Proc. Inst. Mech. Eng., Vol 185, 1970–71, p 285–299

39. S.S. Manson, Time-Temperature Parameters—A Re-evaluation and Some New Approaches, in Time-

Temperature Parameters for Creep-Rupture Analysis, American Society for Metals, 1968, p 1–113

40. S. Manson and C.R. Ensign, “A Specialized Model for Analysis of Creep Rupture Data by the

Minimum Commitment Station-Function Approach,” NASA TM X-52999, 1971, p 1–14

41. S.S. Manson and C.R. Ensign, Interpolation and Extrapolation of Creep Rupture Data by the Minimum

Commitment Method. Part I: Focal-Point Convergence, in Characterization of Materials for Service at

Elevated Temperature, American Society of Mechanical Engineers, New York, 1978, p 299–398

42. S.S. Manson and A. Muralidharen, Analysis of Creep Rupture Data for Five Multiheat Alloys by the

Minimum Commitment Method Using Double Heat Centering Technique, in Progress in Analysis of

Fatigue and Stress Rupture, American Society of Mechanical Engineers, New York, 1984, p 1–46

Assessment and Use of Creep-Rupture Properties

Howard R. Voorhees, Materials Technology Corporation Martin Prager, Materials Properties Council

Estimation of Required Properties Based on Insufficient Data

Complete independent evaluation of creep-rupture properties for a new lot of material, whether by graphical,

parametric, or minimum commitment methods, requires numerous test points covering an extensive range of

test variables. Frequently, the amount of data available is too limited for full treatment by usual procedures.

Experimental difficulties often limit obtaining accurate test results at conditions of interest, such as evaluation

of creep-rupture properties near the low end of the temperature range in which time-dependent effects are

significant.

Tests of short or moderate duration at these temperatures frequently require use of such high stress levels that

the immediate high plastic strains at load application alter the nature of the material from that which exists

during service under lower stresses. Testing at or near a stress of intended application often requires more time

and/or expense than is feasible before the material is to be put into use. Approximate methods permit such

difficulties to be treated in a generally satisfactory manner. Established correlations also permit estimation of

some unmeasured properties from other types of available results.

The Monkman-Grant Relationship. Analysis of data for a variety of aluminum-, iron-, nickel-, titanium-, cobalt-

, and copper-base alloys led Monkman and Grant to the following empirical relationship (Ref 43):

log t

+ m log (mcr) = C

(Eq 7)

where t

is time to rupture; mcr is minimum creep rate; and m and C are constants that differ significantly

among alloy groups, but exhibit nearly fixed values for a given heat of material, or for different lots within the

same alloy group.

Equation 7 enables assessment of the reliability of each individual test by examining its fit within the scatter

band for all tests. Once a minimum creep rate has been determined in a low-stress test, rupture life can be

estimated without running the test to failure. Although Monkman and Grant stated that this relationship was not

intended for extrapolation, it can be used for that purpose, particularly when only low-stress tests are acceptable

to prevent large initial plastic strains.

Table 1 includes the results obtained when the Monkman-Grant relationship is applied to data obtained on these

same seven materials (Ref 37). Overall prediction of rupture life for these 46 extrapolations using this technique

was more accurate than that provided by any of the five time-temperature parameters.

For additional materials (Ref 44) where good fit is obtained to a single linear plot on the coordinates of log time

versus log secondary creep rate, extrapolation of a known secondary creep rate to the corresponding rupture life

appears to be as good or better than by other extrapolation methods. One advantage of Eq 7 is that it can be

applied successfully to as few as four to six data points, in contrast to the approximately 30 tests needed to

establish the entire Manson-Haferd master curve (Ref 45). For the minimum commitment method, even more

data points are usually required.

One advantage of this correlation, particularly with materials that exhibit structural instability under testing, is

that the specimens used to determine the input data for secondary creep rates experience the same history of

structural change that exists during the corresponding period of a test carried to rupture. Best predictions result

by concentrating on tests encompassing a limited range of stresses and temperatures.

Reduced scatter was noted (Ref 46) for eight nonferrous alloys and two superalloys when the term log t

in Eq 7

was replaced by log (t

/ε

), where ε

is the total creep deformation at fracture. This trend was confirmed by Ref

47 in tests on a 2.25Cr-1Mo steel.

Although deformation-modified rupture time may improve correlation in some instances, other cases exist

where use of the original relationship is sufficient or better. Data for 17 test points for 4% cold-worked type 304

stainless steel (Ref 48) exhibited a spread in creep elongation from 1.5 to 24%. Goodness of fit was identical

(coefficient of determination r

= 0.86) for linear regression of the data treated by the original versus the

modified log-log relationships.

Extrapolation is fast and direct when using the Monkman-Grant coordinates, but with the modified relationship,

creep elongation at the given temperature and corresponding to the rupture time sought must first be estimated.

This usually requires subjective extrapolation of only a few elongation values displaying wide scatter and with

no evident single trend. Introduction of a creep elongation factor may have value when only correlation or

interpolation of test results is desired, but it is not recommended for extrapolation.

One occasional problem in estimation of rupture life from creep data is uncertainty whether secondary creep

has truly been established. Changes in creep rate with continuing test time are often sufficiently gradual and so

close to the sensitivity of measurement that what appears to be a steady-rate condition may in fact still be a late

portion of primary creep. Reference 49 illustrates successive apparent minimum creep rates of 2.05, 1.7, and

1.40%/10,000 h for respective test durations of 1000, 2000, and 5000 h.

A distinctive slope change in a plot of log creep rate versus time or log time often provides better assurance that

the secondary creep period has been entered than study of the deformation-time curve itself. Although an

equation expressing true strain in terms of elapsed time, secondary creep rate, and three constants deviates

markedly from actual behavior during the early portion of primary creep, a statistical analysis such as that

detailed in Ref 50 may predict acceptable values of secondary creep rate from transient data.

For type 316 stainless steel tested at 704 to 830 °C (1300–1525 °F), the initial transient rate at t = 0 was found

to be almost equal to 3.3 times the secondary creep rate in the same test (Ref 51). A significantly different

magnitude (near 1000) for this ratio of initial and secondary creep rates was found in Ref 52 for a high-

temperature alloy. A simple proportionality of this type and the more general analysis cited above are tempting

alternatives to permit shortened test durations, but both suffer from the need for creep measurements that are

more precise than those commonly obtained. Currently, neither method is capable of replacing long-time

testing.

The Gill-Goldhoff Method. Many designs for elevated-temperature service require that deformation not exceed

some maximum value; in these cases, creep strain rather than rupture life becomes the focus. Although

published compilations and computer banks of data include rupture properties for most materials of engineering

interest, corresponding information on the time-dependency of strain is frequently sparse or nonexistent. Many

early studies did not include strain measurement during rupture tests. When creep data were obtained, accuracy

was sometimes questionable due to inadequate control of temperature or low precision of strain measurements.

Frequently, the only listed creep data are minimum creep rates. Most of these results were obtained from tests

that were terminated after a few thousand hours, or even less, and true secondary creep rate may not have

become established.

Studies by the Metal Properties Council (now the Materials Properties Council, or MPC) and similar groups

attempt to report both the total strain on loading and the times to various levels of creep strain. Until such

results are more universally available, creep strain to be expected in given design situations must still be

estimated.

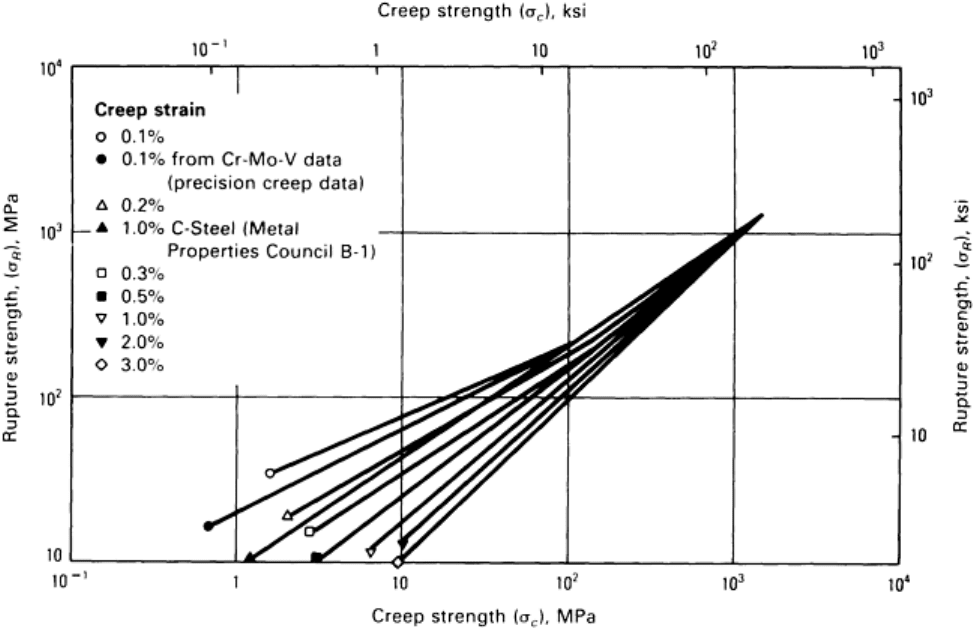
Gill and Goldhoff (Ref 49, 53) found a log-log correlation between stress to cause rupture and stress for a given

creep strain for the same time and temperature. Figure 9 shows their composite plot for aluminum-base alloys

and stainless steels, including several superalloys.

Fig. 9 Composite graph for the Gill-Goldhoff correlation. Source: Ref 53

To obtain this correlation, tests in which 0.1% creep occurred in less than 100 h were rejected to prevent

intolerable data scatter. Despite this, the “universal” curves of Fig. 9 can be associated with fairly wide data

scatter, particularly at low creep strains. Some deviations from the correlation were related to microstructural

instabilities, which produce differing proportions of primary, secondary, and tertiary creep among alloys and

for varying test conditions.

Despite occasional anomalies, the Gill-Goldhoff correlation meets some preliminary design needs, particularly

if the technique is tailored to grades of alloys similar to those of immediate concern. In principle, this technique

can also be used to predict rupture properties from early creep measurements from tests that are not continued

to rupture. This use is limited by the short rupture times that are derived from tests terminated at creep strains of

1% or less. If these tests were continued to higher levels of creep, improved predictions of rupture should be

obtained by determining the secondary creep rate and then applying the Monkman-Grant relationship.

Treatment of Isolated Test Points. Particularly at the start of a testing program, the need may arise to extract

information from a single available test. The form of most parameters limits their use to situations in which

multiple test results are available. The Larson-Miller parameter is an exception if the generalized constant C =

20 is used.

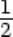
For the stress of the test, longer rupture times within a factor of ten from the test duration frequently can be

estimated satisfactorily for temperatures below that of the test. If a master curve or graph of isothermals is

available for another lot of like or similar alloy, a parallel curve passed through the coordinates of the test point

for the new lot can serve as an approximate representation of expected behavior for limited ranges of variables

from the test conditions.

References cited in this section

37. R.M. Goldhoff and G.J. Hahn, Correlation and Extrapolation of Creep-Rupture Data of Several Steels

and Superalloys Using Time-Temperature Parameters, in Time-Temperature Parameters for Creep-

Rupture Analysis, American Society for Metals, 1968, p 199–245

43. F.C. Monkman and N.J. Grant, An Empirical Relationship Between Rupture Life and Minimum Creep

Rate in Creep-Rupture Tests, Proc. ASTM, Vol 56, 1956, p 593–605

44. H.R. Voorhees, “Determination of Rupture Strength at Temperatures Near the Lower End of the Time-

Dependent Range,” findings reported to the Metal Properties Council, Inc., New York, 1984

45. S. Manson and W.F. Brown, Jr., Discussion to a Paper by F. Garofalo et al., Trans. ASME, Vol 78 (No.

7), Oct 1956, p 143

46. F. Dobeš and K. MiliXXke, The Relation Between Minimum Creep Rate and Time to Fracture, Met.

Sci., Vol 10, Nov 1976, p 382–384

47. D. Lonsdale and P.E.J. Flewitt, Relationship Between Minimum Creep Rate and Time to Fracture for 2-

%Cr-1%Mo Steel, Met. Sci., May 1978, p 264–265

48. M. Gold, W.E. Leyda, and R.H. Zeisloft, The Effect of Varying Degree of Cold Work on the Stress-

Rupture Properties of Type 304 Stainless Steel, Trans. ASME J. Eng. Mat. Technol., Vol 97 (No. 4),

Series H, Oct 1975, p 305–312

49. R.F. Gill and R.M. Goldhoff, Analysis of Long-Time Creep Data for Determining Long-Term Strength,

Met. Eng. Quart., Vol 10 (No. 3), Aug 1970, p 30–39

50. P.L. Threadgill and B.L. Mordike, The Prediction of Creep Life From Transient Creep Data, Z.

Metallkd., Vol 68 (No. 4), 1977, p 266–269

51. F. Garofalo, C. Richmond, W.F. Domis, and F. von Gemmingen, Strain-Time, Rate-Stress and Rate-

Temperature Relations During Large Deformations in Creep, Joint International Conference on Creep,

Institution of Mechanical Engineers, London, 1963, p 1-31 to 1-39

52. P.L. Threadgill and B. Wilshire, Mechanisms of Transient and Steady-State Creep in a γ′-Hardened

Austenitic Steel, in Creep Strength in Steel and High-Temperature Alloys, The Metals Society, London,

1974, p 8–14

53. R.M. Goldhoff and R.F. Gill, A Method for Predicting Creep Data for Commercial Alloys on a

Correlation Between Creep Strength and Rupture Strength, Trans. ASME J. Basic Eng., Vol 94 (No. 1),

Series D, March 1972, p 1–6

Assessment and Use of Creep-Rupture Properties

Howard R. Voorhees, Materials Technology Corporation Martin Prager, Materials Properties Council

Evaluating Remaining Creep-Rupture Life

Expected residual rupture life following a discrete change in service conditions may at times be estimated

without further tests. The more usual practice is to test creep-exposed samples at increased stress and/or

temperature than they had seen in service, to reduce testing duration. Results are then extrapolated back to

nominal service conditions. In addition to parametric methods and isostress methods, at least three others

procedures have found recent promotion:

• The MPC Omega Method

• Analysis on restricted-range Monkman-Grant coordinates

• Accelerated creep-test methodology of David Woodford

These methods are described in the section “Other Evaluation Methods” in this article.

Discrete Changes in Temperature or Stress. When a creep-rupture test is interrupted by cooling and reheating at

a moderate rate at constant load, and if the time under changing temperature is brief compared to the original

test duration, the effect of the interruption on either the creep curve or rupture life usually cannot be readily

detected, unless thermal gradients cause gross plastic deformation or spalling of surface layers.

Similar results can be expected when temperature and stress rise and fall in unison, as during start-up and

shutdown of a steam boiler. For the alternate situation in which unloading occurs while the creep temperature is

maintained, significant recovery of primary creep can ensue; reapplying the load results in a period of primary

creep.

Under step-wise alteration of load, temperature, or both during a test or service, performance often roughly

follows the “life-fraction rule” or “linear cumulative damage rule” (Ref 54), in which the percentage of total life

consumed for each period of fixed temperature and stress is represented as:

Accuracy of this rule ranges from excellent to rather poor, with best results for multiple small excursions (Ref

55). Although solid-state reactions, which can reverse at different exposure temperatures, may introduce

complications under some conditions, investigators have found the life-fraction rule more appropriate for steels

under temperature changes than under stress changes (Ref 56).

Life-fraction summations at failure as low as 0.36 and as high as 2.43 have been reported (Ref 57). The spread

was only from 0.75 to 1.50 for the same tests using damage fractions defined by K(t/t

) + (1 - K)(ε/ε

), where t

and ε are the time and strain under a period of fixed conditions, for which the rupture time and fracture strain

are t

and ε

. K is a material constant ranging from zero to 1; the zero limit applies to materials that develop

cracks early in life, and K approaches 1 for materials that exhibit no cracking until rupture is imminent. Typical

values of K (Ref 57) are as follows:

Material and test temperature

Copper at 250 °C (482 °F)

0.3

A 286 alloy at 649 °C (1200 °F), solution treated at 1204 °C (2200 °F)

0.47

A 286 alloy at 649 °C (1200 °F), solution treated at 982 °C (1800 °F)

0.43

Inconel X-750 at 732 °C (1350 °F) 0.625

When data are insufficient for determination of K, acceptable results frequently can be obtained with an

empirical rule (Ref 58), by which the life-fractions added are defined by . With any of these

cumulative damage rules, comparison usually is against rupture life from constant-load tests—that is, with

actual stress rising as creep reduces the cross section. When the same specimen undergoes load changes for

different periods, respective stress levels have been based on the initial cross section. This corresponds to using

the same original load if an interrupted test must be restarted. The actual stress at the time of test restart is

(σ

), where σ

is the present nominal stress, A

is the initial specimen cross section, and A

is the

specimen cross section after creep deformation up to the time of the test interruption.

When the specimen for a test in a later portion of creep has been machined from a part that has already

undergone considerable reduction in cross section by prior creep, a corresponding area-modified stress must be

employed for consistent interpretation of the results (Ref 59). The load applied to produce the desired nominal

stress σn, related to the virgin material is calculated to make the actual stress σ

= σ

), where the latter

term relates cross-sectional areas of the original part before and after creep. Use of such an area-modified stress

has been reported to improve prediction of remaining life from post-service rupture tests (Ref 59, 60).

An approximation of remaining rupture life for components that have undergone prolonged service can be

calculated by introducing best estimates for operating temperatures and stresses into the above damage rules.

More exact evaluation, however, can be obtained by testing representative samples removed from service.

Measurement of Creep-Rupture Properties After Service. Dependable application of techniques to estimate

remaining life requires that the loading direction for the final test corresponds to the largest principal stress of

service and that the specimen is representative of surface deterioration or other damage present in the part.

Possible temperature and loading gradients in service must be kept in mind when selecting a sampling site and

when applying test results to predictions of further serviceability. Despite these possible additional variables,

assessments of post-service rupture properties require only about the same number and duration of tests as

conventional evaluation of any new lot of familiar material.

Large specimens are recommended to limit relative loss in cross section from oxidation, unless surfaces are

protected from the usual air environment of tests.

For samples from tubes or similar shapes subjected to internal-pressure service and consequent major service

stress in the circumferential direction, uniaxial creep tests are preferred to have the test load act in that

direction. Specimens from tube and pipe can have wedges of similar material welded to the outside-diameter

face near the ends of a ring segment from the sample. Electron-beam welded attachments of imaginative design

make possible the testing of many samples available only in small sizes or inconvenient shapes.

Isostress Tests. A typical study involves testing three or four specimens all at a single stress similar to, or

slightly above, the stress of service, and each at a different temperature higher than that of service. Results are

extrapolated to service temperature on coordinates of log rupture time versus either absolute temperature or its

reciprocal.

The principal drawback of this procedure is that at least some tests must usually be conducted at a higher

temperature than is needed in other evaluation methods.

Allowance for Data Scatter. In an effort to minimize uncertainties from extrapolation procedures, undue

emphasis may be placed on a test with the longest affordable duration. Normal data scatter still limits

evaluation of expected performance from isolated points. Indeed, a more reliable prediction may be obtained

when the same total test time is devoted to performing a greater number of tests with intermediate duration

rather than only a few with extended life. An exception is when instabilities occur only with very long testing.

Some researchers study scatter by running multiple tests at one or more fixed combinations of stress and

temperature. Again, a series of tests, each at different conditions, permits equally good statistical treatment to

evaluate the scatter, while providing a broader indication of the material characteristics. Although emphasis has

been placed on time to rupture, the extra expense of obtaining complete creep deformation data in all tests is

often justified by the insight afforded into the effects of structural changes.

References cited in this section

54. E.L. Robinson, Effect of Temperature Variation on the Creep Strength of Steels, Trans. ASME, Vol 60,

1938, p 253–259

55. P.N. Randall, Cumulative Damage in Creep-Rupture Tests of a Carbon Steel, Trans. ASME J. Basic

Eng., Vol 84 (No. 2), Series D, June 1962, p 239–242

56. D.A. Woodford, Creep Damage and Remaining Life Concept, Trans. ASME J. Eng. Mat. Technol., Vol

101 (No. 4), Dec 1979, p 311–316

57. M.M. Abo El Ata and I. Finnie, A Study of Creep Damage Rules, Trans. ASME J. Basic Eng., Vol 94

(No. 3), Series D, Sept 1972, p 533–543

58. J.W. Freeman and H.R. Voorhees, “Notch Sensitivity of Aircraft Structural and Engine Alloys, Part II:

Further Studies with A-286 Alloys,” Wright Air Development Center, Technical Report 57–58, ASTIA

Document 207,850, Jan 1959

59. R.V. Hart, Concept of Area-Modified Stress for Life-Fraction Summation During Creep, Met. Technol.,

Sept 1977, p 447–448

60. R.V. Hart, Assessment of Remaining Creep Life Using Accelerated Stress-Rupture Tests, Met.

Technol., Jan 1976, p 1–7